鲁教版(五四学制)七年级上册1.1认识三角形课件(共33张PPT)
文档属性
| 名称 | 鲁教版(五四学制)七年级上册1.1认识三角形课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 19:10:47 | ||
图片预览






文档简介
(共33张PPT)
三角形
01
学习目标
02
三角形
03
当堂检测
04
课堂总结
目录
CONTENTS
PART O1
学习目标
学习目标
1.强化三角形的三边关系及面积计算
2.强化三角形的内角和外角定理(重难点)
3.强化三角形的三线(重难点)
PART O2
三角形
三角形
三角形 定义 由不在同一条直线上的三条线段 所组成的图形叫做三角形
边 组成三角形的 叫做三角形的边
顶点 相邻两条公共端点叫做三角形的顶点。
角 相邻两条边所组成的角,叫做三角形的 ,简称三角形的角。
面积 三角形的面积= ×底×高
线段
内角
首尾相接
三角形
1.判断对错:
(1)由三条线段组成的图形叫做三角形. ( )
(2)三角形的内角简称三角形的角. ( )
(3)图中有两个三角形. ( )
×
√
×
三角形
三角形的分类
1.按角分
锐角三角形
直角三角形
钝角三角形
2.按边分
不等边三角形
等腰三角形
底和腰不等的等腰三角形
等边三角形
(三个角都是锐角的三角形)
(有一个角为直角的三角形)
(有一个角为钝角的三角形)
把边和角联系在一起组成特殊的三角形
等腰直角三角形
(两条直角边相等的直角三角形)
跟踪练习
1、在△ABC中,∠A=10°∠B=60°则△ABC的形状是( )
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等边三角形
A
2、在△ABC中,若∠A:∠B:∠C=1:3:5,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.形状不确定
C
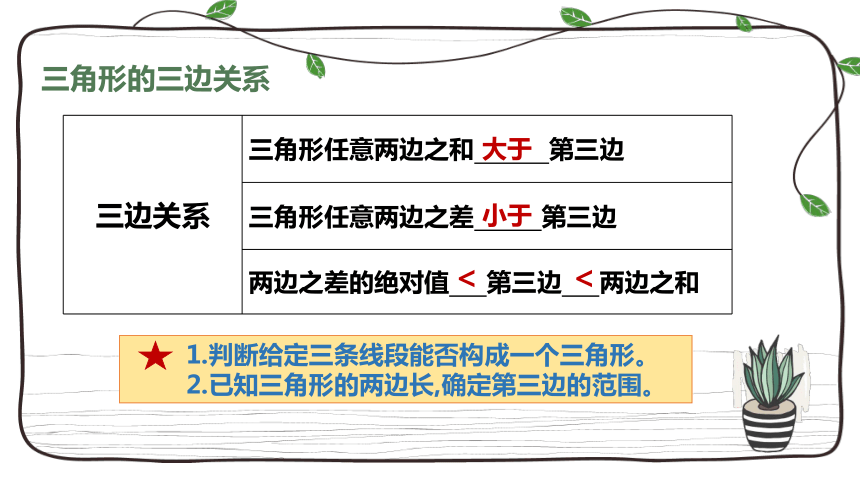
三角形的三边关系
三边关系 三角形任意两边之和 第三边
三角形任意两边之差 第三边
两边之差的绝对值 第三边 两边之和
大于
小于
<
<
1.判断给定三条线段能否构成一个三角形。
2.已知三角形的两边长,确定第三边的范围。
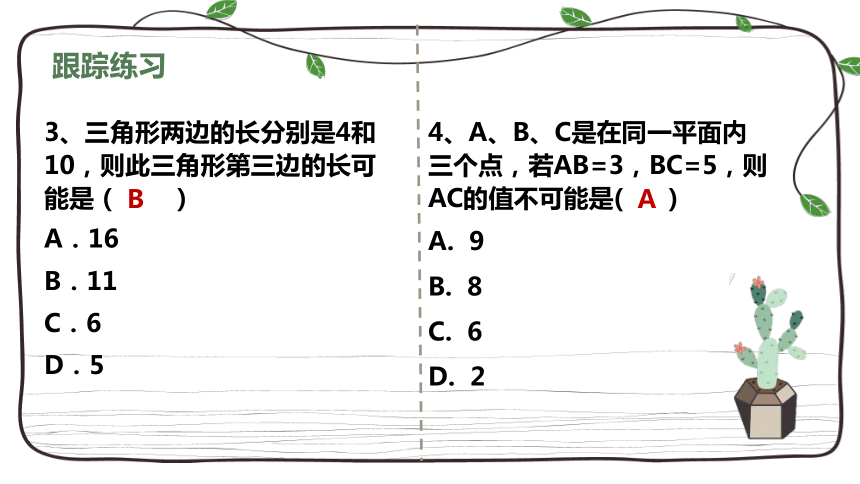
跟踪练习
3、三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.16
B.11
C.6
D.5
B
4、A、B、C是在同一平面内三个点,若AB=3,BC=5,则AC的值不可能是( )
A. 9
B. 8
C. 6
D. 2
A
三角形的三边关系
内角和与 外角和 三角形的内角和等于 .
直角三角形的两个锐角 .
三角形的一个外角 和它不相邻的来两个内角的和
三角形的一个外角 任何一个和它不相邻的内角
180°
互余
等于
大于
跟踪练习
5、如图AB∥CD,∠1=50°,∠2=45°,则∠CAD的大小是( )
A.75°
B.80°
C.85°
D.90°
C
6、如图,三角形ABC中,BE平分∠ABC,CE平分∠ACD,若∠A=50°,则∠BEC的度数为 .
25°
三角形的角平分线
三角形的角平分线 定义 三角形一个角的 与这个角的对边相交,角的顶点和交点之间的 叫做三角形的角平分线
数量 一个三角形有 条角平分线
位置 都在三角形 ,并且相交于一点。
提示 1、三角形的角平分线是一条 。
2、角的平分线是一条 。
线段
三
内部
线段
射线
平分线
三角形的中线
三角形的中线 定义 在三角形中,连接一个顶点与对边 的 叫做这个三角形的中线。
数量 一个三角形有 条平分线
位置 都在三角形 ,并且相交于一点,这个点叫做三角形的 。
提示 1.三角形的中线是一条 。
2.角的每一条中线都将三角形分成两个面积 的三角形。
中点
三
内部
线段
相等
线段
重心
三角形的高
三角形的高 定义 三角形一个顶点到他对边所在直线的 叫做这个三角形的高
数量 一个三角形都有 条高。
位置 1.锐角三角形的高交于三角形 一点
2.直角三角形的高交于 。
3.钝角三角形的高的延长线交于三角形 一点。
提示 1.三角形的中线是一条 。
三
内部
外部
垂线段
垂线段
直角顶点
跟踪练习
7、下列说法正确的是( )
A.三角形的三条高至少有一条在三角形内
B.直角三角形只有一条高
C.三角形的角平分线其实就是角的平分线
D.三角形的角平分线、中线、高都在三角形的内部
A
8、下列叙述不正确的是( )
A.三角形的三条角平分线交于一点(内心),这个点一定在三角形的内部
B.三角形的三条中线交于一点(重心),这个点一定在三角形的内部
C.三角形的三条高线交于一点(垂心),这个点一定在三角形的内部
D.三角形内角的平分线、高线、中线都是线段。
C
跟踪练习
C
1.如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中 ( )
A.①②都正确
B.①②都不正确
C.①正确,②不正确
D.①不正确,②正确
跟踪练习
如图,AD⊥BC,垂足为D,∠BAC=∠CAD,下列说法正确的是 ( )
A.直线AD是△ABC的边BC上的高
B.线段BD是△ABD的边AD上的高
C.射线AC是△ABD的角平分线
D.△ABC与△ACD的面积相等
B
PART O3
当堂检测
当堂检测
1、根据下列条件,不能判断△ABC形状的是( )
A. AB=BC B. ∠A=80°
C. ∠A=50°,∠B=70° D. ∠A﹣∠B=∠C
B
2、已知三角形ABC的三边a,b,c满足(a+b)2+|b-c|=0,则△ABC形状的是( )
A. 钝角三角形 B. 直角三角形
C. 等边三角形
D. 以上都不对
C
当堂检测
4、图中三角形的个数是( )A. 3个
B. 4个
C. 5个
D. 6个
3、如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上,如果∠2=60°,那么∠1的度数为 ( )
A.60°
B.50°
C.40°
D.30°
D
D
当堂检测
5、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE,如果∠A=α ,∠CEA'=β,∠BDA'=γ ,那么下列式子正确的是( )
A. γ=2α+β
B. γ=α+2β
C. γ=α+β
D. γ=180°-α-β
A
当堂检测
6、如图所示,∠B+∠C+∠D+∠E-∠A等于( )
A. 360°
B. 300°
C. 180°
D. 240°
C
当堂检测
7、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= ( )
A.1
B.2
C.3
D.4
B
当堂检测
8、如果一个等腰三角形的两边长分别是3和5,则它的周长为 。
9、如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC= .
10、如图,∠A=28°,∠BFC=92°,∠B=∠C,则∠BDC的度数是 .
11或13
100°
80°
当堂检测
11、如图,在△ABC中,点D是AB上一点,点E是AC上一点,BE,CD相交于点F,∠A=72°,∠ACD=35°,∠ABE=20°.
求:(1)∠BDC的度数
(2)∠BFD的度数
当堂检测
12、如图所示,在△ABC,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD:BE的值.
当堂检测
13、如图13-10(1),在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于点D.
(1)试推导∠EFD与∠B,∠C的大小关系.
(2)如图13-10(2),当点F在AE的延长线上时,其余条件都不变,判断(1)中推导的结论是否还成立?
PART O4
课堂总结
课堂总结
三角形的定义及表示方法;分类(边、角)
三角形的高、中线、角平分线的定义及性质
三角形
三角形的三边关系;外角定义及性质
感谢聆听!
三角形
01
学习目标
02
三角形
03
当堂检测
04
课堂总结
目录
CONTENTS
PART O1
学习目标
学习目标
1.强化三角形的三边关系及面积计算
2.强化三角形的内角和外角定理(重难点)
3.强化三角形的三线(重难点)
PART O2
三角形
三角形
三角形 定义 由不在同一条直线上的三条线段 所组成的图形叫做三角形
边 组成三角形的 叫做三角形的边
顶点 相邻两条公共端点叫做三角形的顶点。
角 相邻两条边所组成的角,叫做三角形的 ,简称三角形的角。
面积 三角形的面积= ×底×高
线段
内角
首尾相接
三角形
1.判断对错:
(1)由三条线段组成的图形叫做三角形. ( )
(2)三角形的内角简称三角形的角. ( )
(3)图中有两个三角形. ( )
×
√
×
三角形
三角形的分类
1.按角分
锐角三角形
直角三角形
钝角三角形
2.按边分
不等边三角形
等腰三角形
底和腰不等的等腰三角形
等边三角形
(三个角都是锐角的三角形)
(有一个角为直角的三角形)
(有一个角为钝角的三角形)
把边和角联系在一起组成特殊的三角形
等腰直角三角形
(两条直角边相等的直角三角形)
跟踪练习
1、在△ABC中,∠A=10°∠B=60°则△ABC的形状是( )
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等边三角形
A
2、在△ABC中,若∠A:∠B:∠C=1:3:5,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.形状不确定
C
三角形的三边关系
三边关系 三角形任意两边之和 第三边
三角形任意两边之差 第三边
两边之差的绝对值 第三边 两边之和
大于
小于
<
<
1.判断给定三条线段能否构成一个三角形。
2.已知三角形的两边长,确定第三边的范围。
跟踪练习
3、三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.16
B.11
C.6
D.5
B
4、A、B、C是在同一平面内三个点,若AB=3,BC=5,则AC的值不可能是( )
A. 9
B. 8
C. 6
D. 2
A
三角形的三边关系
内角和与 外角和 三角形的内角和等于 .
直角三角形的两个锐角 .
三角形的一个外角 和它不相邻的来两个内角的和
三角形的一个外角 任何一个和它不相邻的内角
180°
互余
等于
大于
跟踪练习
5、如图AB∥CD,∠1=50°,∠2=45°,则∠CAD的大小是( )
A.75°
B.80°
C.85°
D.90°
C
6、如图,三角形ABC中,BE平分∠ABC,CE平分∠ACD,若∠A=50°,则∠BEC的度数为 .
25°
三角形的角平分线
三角形的角平分线 定义 三角形一个角的 与这个角的对边相交,角的顶点和交点之间的 叫做三角形的角平分线
数量 一个三角形有 条角平分线
位置 都在三角形 ,并且相交于一点。
提示 1、三角形的角平分线是一条 。
2、角的平分线是一条 。
线段
三
内部
线段
射线
平分线
三角形的中线
三角形的中线 定义 在三角形中,连接一个顶点与对边 的 叫做这个三角形的中线。
数量 一个三角形有 条平分线
位置 都在三角形 ,并且相交于一点,这个点叫做三角形的 。
提示 1.三角形的中线是一条 。
2.角的每一条中线都将三角形分成两个面积 的三角形。
中点
三
内部
线段
相等
线段
重心
三角形的高
三角形的高 定义 三角形一个顶点到他对边所在直线的 叫做这个三角形的高
数量 一个三角形都有 条高。
位置 1.锐角三角形的高交于三角形 一点
2.直角三角形的高交于 。
3.钝角三角形的高的延长线交于三角形 一点。
提示 1.三角形的中线是一条 。
三
内部
外部
垂线段
垂线段
直角顶点
跟踪练习
7、下列说法正确的是( )
A.三角形的三条高至少有一条在三角形内
B.直角三角形只有一条高
C.三角形的角平分线其实就是角的平分线
D.三角形的角平分线、中线、高都在三角形的内部
A
8、下列叙述不正确的是( )
A.三角形的三条角平分线交于一点(内心),这个点一定在三角形的内部
B.三角形的三条中线交于一点(重心),这个点一定在三角形的内部
C.三角形的三条高线交于一点(垂心),这个点一定在三角形的内部
D.三角形内角的平分线、高线、中线都是线段。
C
跟踪练习
C
1.如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中 ( )
A.①②都正确
B.①②都不正确
C.①正确,②不正确
D.①不正确,②正确
跟踪练习
如图,AD⊥BC,垂足为D,∠BAC=∠CAD,下列说法正确的是 ( )
A.直线AD是△ABC的边BC上的高
B.线段BD是△ABD的边AD上的高
C.射线AC是△ABD的角平分线
D.△ABC与△ACD的面积相等
B
PART O3
当堂检测
当堂检测
1、根据下列条件,不能判断△ABC形状的是( )
A. AB=BC B. ∠A=80°
C. ∠A=50°,∠B=70° D. ∠A﹣∠B=∠C
B
2、已知三角形ABC的三边a,b,c满足(a+b)2+|b-c|=0,则△ABC形状的是( )
A. 钝角三角形 B. 直角三角形
C. 等边三角形
D. 以上都不对
C
当堂检测
4、图中三角形的个数是( )A. 3个
B. 4个
C. 5个
D. 6个
3、如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上,如果∠2=60°,那么∠1的度数为 ( )
A.60°
B.50°
C.40°
D.30°
D
D
当堂检测
5、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE,如果∠A=α ,∠CEA'=β,∠BDA'=γ ,那么下列式子正确的是( )
A. γ=2α+β
B. γ=α+2β
C. γ=α+β
D. γ=180°-α-β
A
当堂检测
6、如图所示,∠B+∠C+∠D+∠E-∠A等于( )
A. 360°
B. 300°
C. 180°
D. 240°
C
当堂检测
7、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= ( )
A.1
B.2
C.3
D.4
B
当堂检测
8、如果一个等腰三角形的两边长分别是3和5,则它的周长为 。
9、如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC= .
10、如图,∠A=28°,∠BFC=92°,∠B=∠C,则∠BDC的度数是 .
11或13
100°
80°
当堂检测
11、如图,在△ABC中,点D是AB上一点,点E是AC上一点,BE,CD相交于点F,∠A=72°,∠ACD=35°,∠ABE=20°.
求:(1)∠BDC的度数
(2)∠BFD的度数
当堂检测
12、如图所示,在△ABC,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD:BE的值.
当堂检测
13、如图13-10(1),在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于点D.
(1)试推导∠EFD与∠B,∠C的大小关系.
(2)如图13-10(2),当点F在AE的延长线上时,其余条件都不变,判断(1)中推导的结论是否还成立?
PART O4
课堂总结
课堂总结
三角形的定义及表示方法;分类(边、角)
三角形的高、中线、角平分线的定义及性质
三角形
三角形的三边关系;外角定义及性质
感谢聆听!
