等腰三角形

课件20张PPT。
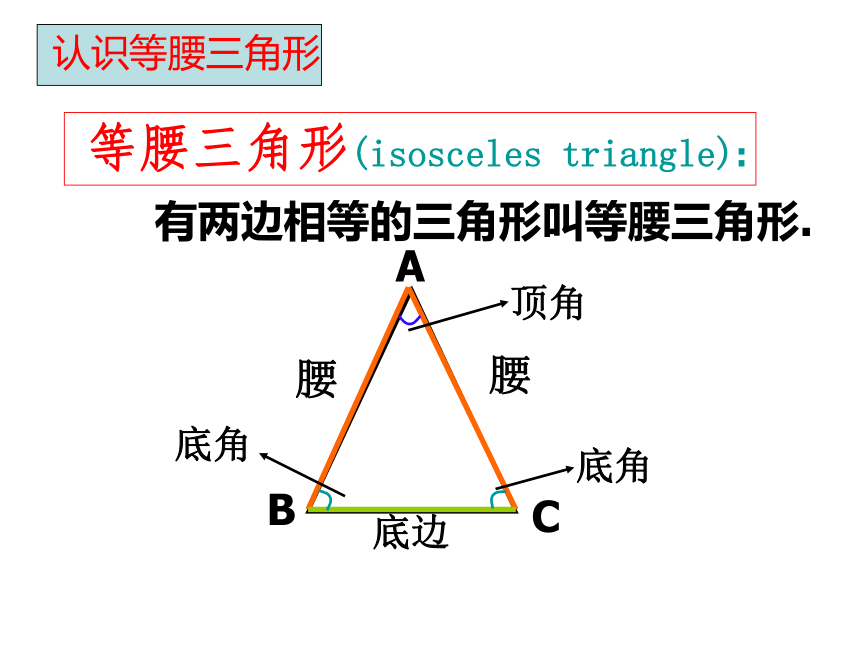
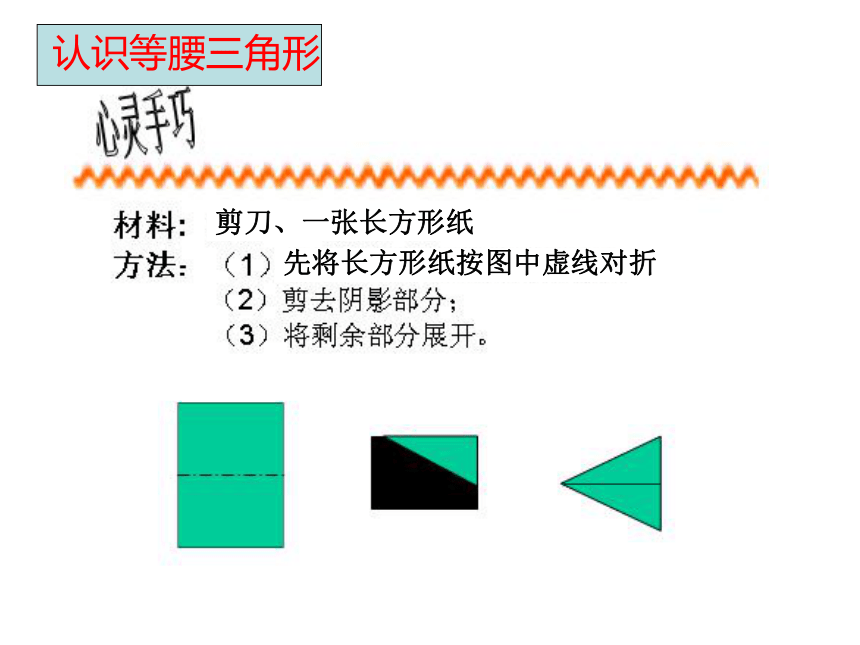
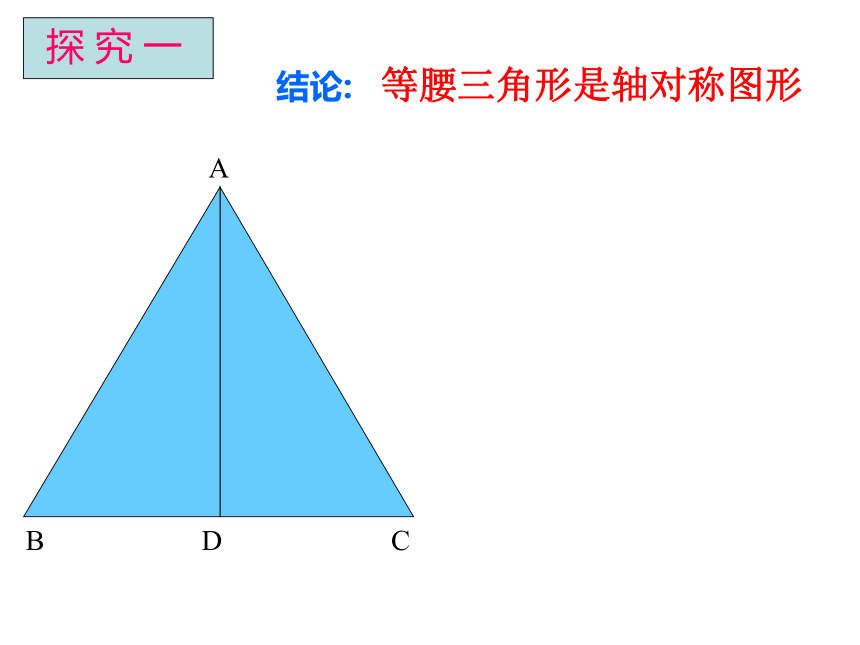
长屿中学　　邬香君有两边相等的三角形叫等腰三角形. 等腰三角形(isosceles triangle):底边剪刀、一张长方形纸先将长方形纸按图中虚线对折CDBA结论: 等腰三角形是轴对称图形

在Rt△ABD和Rt △ACD中
AB=AC （已知）
AD=AD（公共边） ∴Rt△ABD≌Rt△ACD(HL) ∴ ∠B=∠C(全等三角形的对应角相等） 证明：过点A作AD⊥BC于D
∴ ∠ADB=∠ADC=900等腰三角形的两个底角相等等腰三角形的两个底角相等已知：?ABC中 ， AB=AC.
求证： ? B=?C.
证明一:作底边的高AD证明二:作底边的中线AD证明三:作顶角的平分线AD.ACB
在Rt△ABD和Rt △ACD中
AB=AC （已知）
AD=AD（公共边） ∴Rt△ABD≌Rt△ACD(HL) ∴ ∠B=∠C(全等三角形的对应角相等）BD=CD, ∠BAD=∠CAD 证明：过点A作AD⊥BC于D
∴ ∠ADB=∠ADC=900等腰三角形的顶角平分线,底边上
的中线,底边上的高互相重合.探 究 三
等腰三角形性质:
　1.　 等腰三角形是轴对称图形
2.性质1 等腰三角形的两个底角相等
（简写成“等边对等角”）；
　3.性质2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合。
（可简记为“三线合一”）
1 .等腰三角形ABC，若底角为300,那么它的顶角是______.12002.等腰三角形一个角为30°,它的另外两个角为_________________ 75°,75°或 30°,120°3 .如图,在△ABC中,AB=AC, BD=CD，∠BAC=100o,则∠BAD= ______ 4 .如图,在△ABC中,AB=AC, AD平分∠BAC, BC=10则BD= ______50o5 例题讲解
1、在△ABC中，AB=AC，点D在AC上，且BC=BD=AD。
（1）图中共有几个等腰三角形？分别说出每一个等腰三角形的底角。
（2）你能求出△ABC内角的度数吗？
解：∵AB=AC，BC=BD=AD∴∠ABC=∠C ,∠C =∠BDC
∠A=∠ABD （等边对等角） 设∠A=X ，则∠ABD=X ∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中，有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360∴∠A=360，∠ABC=∠C=720 如图在等腰三角形ABC中，AB =AC.点D为BC的中点．AEDCBF(1)猜想一下：点D到两腰的距离DE与DF相等吗？（2）如果DE、DF分别是AB、AC上的中线，它们还相等吗？探一探（3）如果DE、DF是∠ADB、 ∠ ADC的平分线，它们还相等吗？ 如图在等腰三角形ABC中，AB =AC.点D为BC的中点．(1)猜想一下：点D到两腰的距离DE与DF相等吗？（2）如果DE、DF分别是AB、AC上的中线，它们还相等吗？问题拓展（3）如果将点D沿DA由D向A运动到D′那么点D′到两腰的距离还相等吗？试说明理由．（2）如果DE、DF是∠ADB、 ∠ ADC的平分线，它们还相等吗？ADCB● 1 、掌握等腰三角形的两个性质及简单应用 2、熟练求解等腰三角形的顶角、底角的度数；
3 、注意：解决等腰三角形有关计算有时要利
用方程来解决
必做:课本P.143 3题 ，作业本 布置作业 选做:课本P.150习题14.3第8题谢谢