青岛版(五四学制)五年级下册数学图形的认识与测量(课件)(共40张PPT)
文档属性
| 名称 | 青岛版(五四学制)五年级下册数学图形的认识与测量(课件)(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 16:16:19 | ||
图片预览





文档简介
(共40张PPT)
图形的认识与测量
Math courseware
平面图形
周长和面积
总结
立体图形
01
02
03
04
图形的认识与测量
PART 01
平面图形的认识
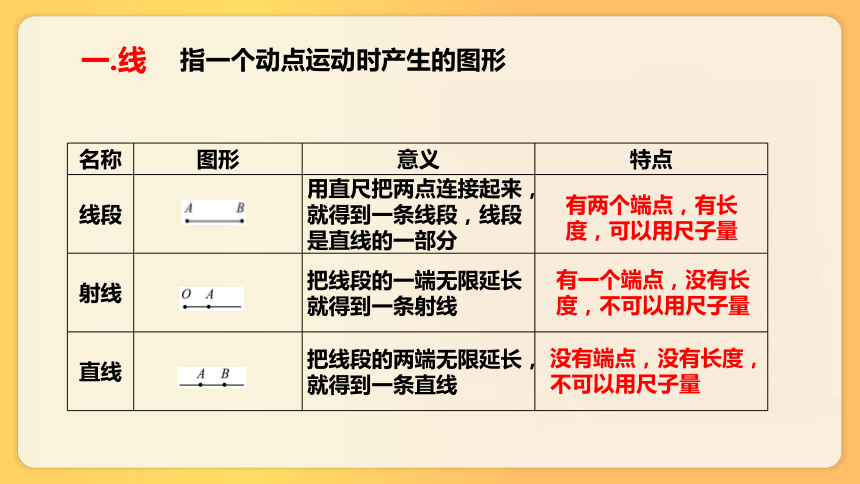
一.线
指一个动点运动时产生的图形
名称 图形 意义 特点
线段 用直尺把两点连接起来,就得到一条线段,线段是直线的一部分
射线 把线段的一端无限延长就得到一条射线
直线 把线段的两端无限延长,就得到一条直线
有两个端点,有长度,可以用尺子量
有一个端点,没有长度,不可以用尺子量
没有端点,没有长度,不可以用尺子量
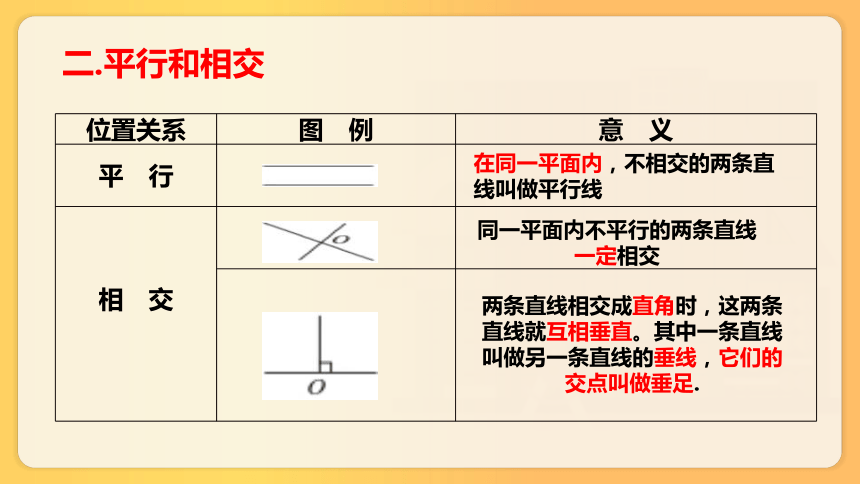
二.平行和相交
位置关系 图 例 意 义
平 行
相 交
在同一平面内,不相交的两条直线叫做平行线
同一平面内不平行的两条直线一定相交
两条直线相交成直角时,这两条直线就互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
三.角
1.具有公共端点的两条_______组成的图形叫做角。这个公共端点叫做角的______,这两条射线叫做角的两条边。角通常用“____ ”来表示。
2.一条射线绕着它的______从一个位置旋转到另一个位置所形成的图形叫做角。所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边。
射线
顶点
∠
端点
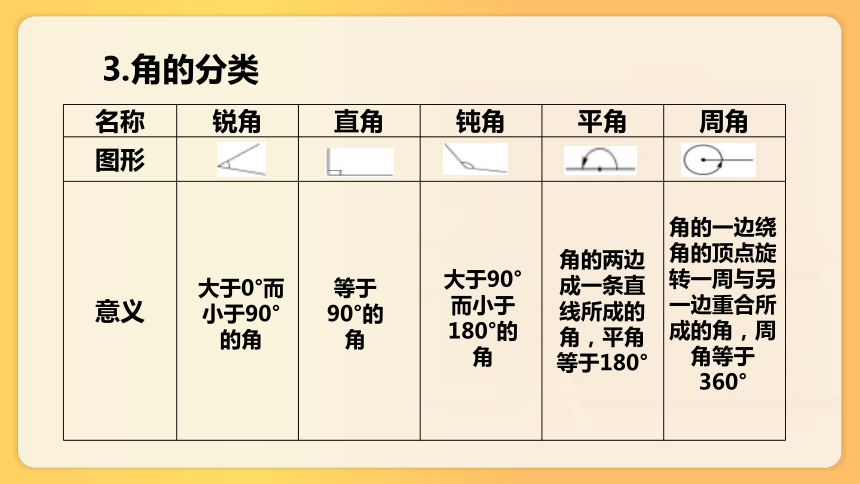
3.角的分类
名称 锐角 直角 钝角 平角 周角
图形
意义
大于0°而小于90°的角
等于90°的角
大于90°而小于180°的角
角的两边成一条直线所成的角,平角等于180°
角的一边绕角的顶点旋转一周与另一边重合所成的角,周角等于360°
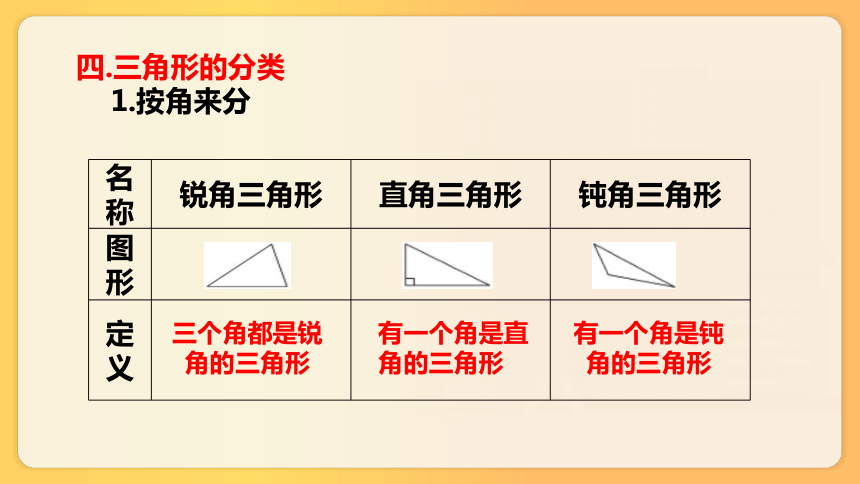
四.三角形的分类
1.按角来分
名称 锐角三角形 直角三角形 钝角三角形
图形
定义
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
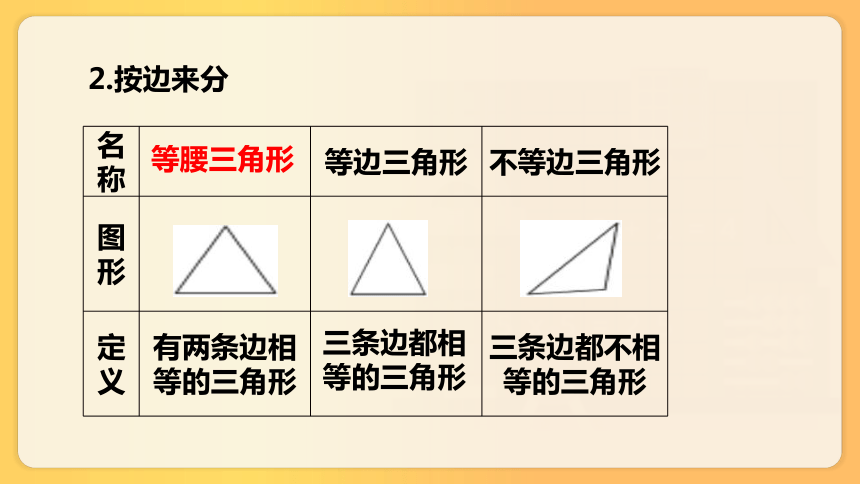
2.按边来分
名称 等边三角形 不等边三角形
图形
定义 有两条边相等的三角形 三条边都不相等的三角形
等腰三角形
三条边都相等的三角形
3.三角形的内角和 三角形的内角和是_________。
4.三角形三条边的关系 ___________________________________。 ___________________________________。
5.三角形的特征 ___________________。
180°
(1)三角形中任意两边之和大于第三边
(2)三角形中任意两边之差小于第三边
三角形具有稳定性
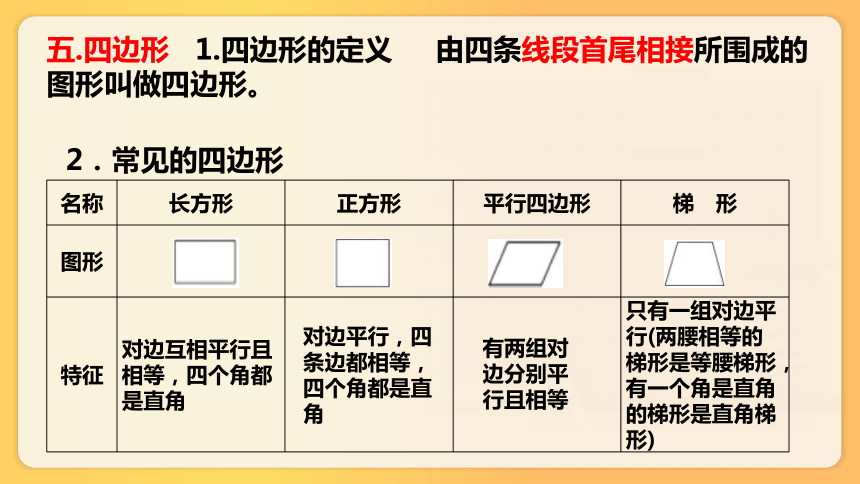
五.四边形 1.四边形的定义 由四条线段首尾相接所围成的图形叫做四边形。
2.常见的四边形
名称 长方形 正方形 平行四边形 梯 形
图形
特征 对边互相平行且相等,四个角都是直角 只有一组对边平行(两腰相等的梯形是等腰梯形,有一个角是直角的梯形是直角梯形)
对边平行,四条边都相等,四个角都是直角
有两组对边分别平行且相等
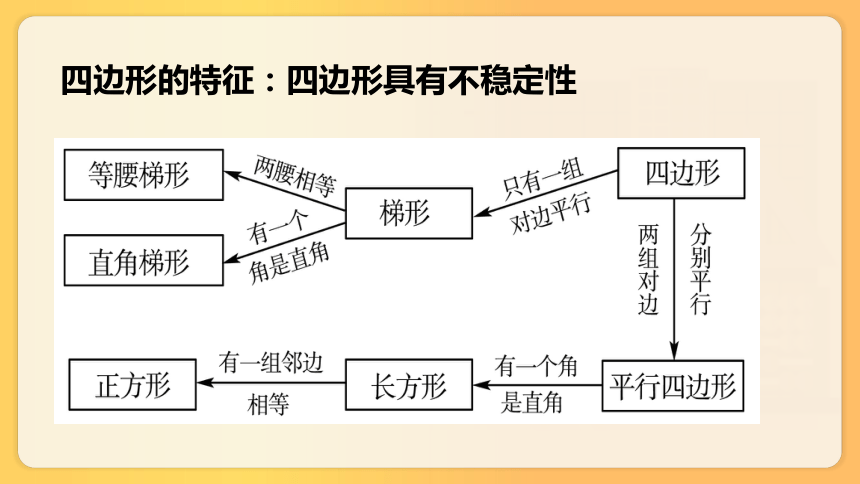
四边形的特征:四边形具有不稳定性
六. 圆
1.圆:圆是平面上的封闭曲线图形。2.圆各部分的名称 圆中心的一点叫做_________,通常用字母O表示,连接圆心和圆上任意一点的线段叫做______,通常用字母r表示,通过圆心并且两端都在圆上的线段叫做_______,通常用字母d表示。
圆心
半径
直径
3.圆心、半径和圆的关系
_________决定圆的位置,_______决定圆的大小。
4.圆的特征(1)在同一个圆内,可以画______条半径,无数条______,所有的半径_________,所有的直径都相等。(2)在同一个圆内,__________________,即d=2r,半径是直径的____,即r=____d。(3)圆是轴对称图形,它有______条对称轴。
圆心
半径
无数
直径
都相等
直径是半径的2倍
无数
七.扇形和圆环
1.扇形 一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,扇形是圆的一部分。
2.圆环
___________________________________________。
同一个圆心不同半径的两个圆所组成的图形
1.3时整,时针和分针成______角,是______度;6时整,时针和分针成______角,是_________度。
2.平角=__________度,周角=__________度,1周角=_________平角=___________直角。
3.下图中,_________和___________互相平行,___________和____________互相垂直,O是__________。
即时训练
4.如下图,从A.B两点各挖一条水渠与河道想通,要是水渠最短,应该怎样挖?请你在图中画出来。如果这幅图的比例尺是 ,那么从A点挖的水渠实际长约多少米?
5.数一数,填一填。
正方形有________个;长方形有________个;圆有________个;三角形有________个。
PART 02
平面图形的周长和面积
常见平面图形的特征及周长、面积计算公式
名 称 正方形 长方形
图 形
字母意义 a—边长 a—长b —宽
特 征
周长C、面积S公式
四条边都相等,四个角都是直角
两组对边相等,四个角都是直角
C=4a S=a2
C=2(a+b) S=ab
名 称 平行四边形 三角形
图 形
字母意义 a—底h—高 a—底h—高
特 征
面积S公式
两组对边分别平行且相等
有三条边和三个角
S=ah
S= ah
名 称 梯 形 圆
图 形
字母意义 a—上底b —下底h—高 r —半径d—直径
特 征
周长C、面积S公式
只有一组对边平行
同一个圆中所有半径相等、所有直径相等,直径等于半径的2倍
C=πd=2πr S=πr2
名 称 扇 形 环 形
图 形
字母意义 r —半径 n°—圆心角度数 r —小圆半径R—大圆半径
特 征 由圆心角和圆心角所对的弧围成
面积S公式
大圆和小圆同圆心,半径不同
πr2
S= ×n
S=πR2-πr2
即时训练
1.根据圆的面积、周长公式解决问题。
计算下列图形的周长和面积。
2. 如图,大正方形的边长是10厘米,小正方形的边长是5厘米,求阴影部分的面积是多少平方厘米?
PART 03
立体图形
观察图形:
从正面看:___________观察物体得到的平面图形
____________:由上向下观察物体得到的平面图形
从左面看:___________观察物体得到的平面图形
由前向后
从上面看
由左向右
立体图形的认识
一.
1.长方体的定义
由_______________(特殊情况下有两个相对的面是正方形)围成的立体图形叫做长方体。
2.正方体的定义
由________________________围成的立体图形叫做正方体。正方体是特殊的长方体,是长、宽、高都相等的长方体。
6个长方形
6个完全相同的正方形
3.长方体和正方体的特征
名 称
图 形
展开图示例
相同点 面
棱
顶点
6个
长方体
正方体
6个
12条
12条
8个
8个
不同点 面的特点 6个面一般都是长方形,也可能有两个相对的面是正方形 6个面都是相同的正方形
面的大小
棱长 相对的棱的长度相等
联 系 正方体是特殊的长方体
相对的面的面积相等
6个面的面积都相等
棱长之和=(长+宽+高)×4=长×4+宽×4+高×4
12条棱的长度都相等棱长之和=棱长×12
二.圆柱和圆锥的定义及特征
1.圆柱的定义 以长方形的一条边所在的直线为轴旋转一周所得到的几何体叫做圆柱。
2.圆锥的定义 以直角三角形的一条直角边所在的直线为轴旋转一周得到的几何体叫做圆锥。
3.圆柱和圆锥的特征
名称 图 形 展开图示例 特 征
圆柱 上下两个底面
两个底面之间的距离
侧面展开图
长方形的长、宽、
圆柱有无数条高
圆锥 下底面
上底面缩成一点叫,
顶点到底面圆心(O)的距离
圆锥的高
圆锥的侧面展开图
1.表面积
______________________________________________。
常用的单位:平方米、平方分米、平方厘米。
2.体积
____________________________________________。
常用的单位:立方米、立方分米、立方厘米。
三 . 常见的立体图形的表面积和体积的基本概念、计算公式
物体表面面积的总和叫做物体的表面积
物体所占空间的大小叫做物体的体积
3.立体图形的表面积和体积计算公式
名称 图 形 字母意义 表(或侧)面积 体 积
正方体 a—棱长
长方体 a—长b—宽h—高
圆 柱 r —底面半径h—高C—底面周长
圆 锥 r —底面半径h—高
S表=6a2
S表=(ab+ah+bh)×2
S侧=Ch=2πrh
S表=S侧+2S底=2πrh+2πr2
V=a3
V=abh
V=S底h =πr2h
V=S底h=πr2h
即时训练
1.一个社区要挖一个长22米、宽10米、深2.5米的蓄水池.蓄水池挖好后,要在底部和四周抹一层水泥,抹水泥的面积有多大?
2.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱组成一个物体。
(1)求这个物体的体积。
(2)求这个物体的表面积。
3.一个长方体,如果长减少2厘米,就变成一个正方体,这个正方体的表面积是96平方厘米,则原来长方体的体积是________立方厘米。
4.一个圆锥与圆柱的底面积相等,已知这个圆柱与圆锥的体积比为1:6,圆锥的高是54厘米,圆柱的高是__________厘米。
5.把32升水倒入一个长8分米、宽2.5分米的长方体水箱内,正好倒满,
这个水箱深__________分米。
6.如图,这个立体图形是用棱长为1厘米的小正方体积木搭成的,
求这个立体图形的表面积、体积。
7.用两个相同的正方体拼成一个长方体,这个长方体的棱长总和是80厘米,每个正方体的表面积是多少?
8.红星小学修一条长60米、宽40米的长方形操场,先铺了10厘米厚的三合土,又铺了4厘米厚的煤渣。需要的三合土比煤渣多多少立方米?
课堂总结
谢谢观看
图形的认识与测量
Math courseware
平面图形
周长和面积
总结
立体图形
01
02
03
04
图形的认识与测量
PART 01
平面图形的认识
一.线
指一个动点运动时产生的图形
名称 图形 意义 特点
线段 用直尺把两点连接起来,就得到一条线段,线段是直线的一部分
射线 把线段的一端无限延长就得到一条射线
直线 把线段的两端无限延长,就得到一条直线
有两个端点,有长度,可以用尺子量
有一个端点,没有长度,不可以用尺子量
没有端点,没有长度,不可以用尺子量
二.平行和相交
位置关系 图 例 意 义
平 行
相 交
在同一平面内,不相交的两条直线叫做平行线
同一平面内不平行的两条直线一定相交
两条直线相交成直角时,这两条直线就互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
三.角
1.具有公共端点的两条_______组成的图形叫做角。这个公共端点叫做角的______,这两条射线叫做角的两条边。角通常用“____ ”来表示。
2.一条射线绕着它的______从一个位置旋转到另一个位置所形成的图形叫做角。所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边。
射线
顶点
∠
端点
3.角的分类
名称 锐角 直角 钝角 平角 周角
图形
意义
大于0°而小于90°的角
等于90°的角
大于90°而小于180°的角
角的两边成一条直线所成的角,平角等于180°
角的一边绕角的顶点旋转一周与另一边重合所成的角,周角等于360°
四.三角形的分类
1.按角来分
名称 锐角三角形 直角三角形 钝角三角形
图形
定义
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
2.按边来分
名称 等边三角形 不等边三角形
图形
定义 有两条边相等的三角形 三条边都不相等的三角形
等腰三角形
三条边都相等的三角形
3.三角形的内角和 三角形的内角和是_________。
4.三角形三条边的关系 ___________________________________。 ___________________________________。
5.三角形的特征 ___________________。
180°
(1)三角形中任意两边之和大于第三边
(2)三角形中任意两边之差小于第三边
三角形具有稳定性
五.四边形 1.四边形的定义 由四条线段首尾相接所围成的图形叫做四边形。
2.常见的四边形
名称 长方形 正方形 平行四边形 梯 形
图形
特征 对边互相平行且相等,四个角都是直角 只有一组对边平行(两腰相等的梯形是等腰梯形,有一个角是直角的梯形是直角梯形)
对边平行,四条边都相等,四个角都是直角
有两组对边分别平行且相等
四边形的特征:四边形具有不稳定性
六. 圆
1.圆:圆是平面上的封闭曲线图形。2.圆各部分的名称 圆中心的一点叫做_________,通常用字母O表示,连接圆心和圆上任意一点的线段叫做______,通常用字母r表示,通过圆心并且两端都在圆上的线段叫做_______,通常用字母d表示。
圆心
半径
直径
3.圆心、半径和圆的关系
_________决定圆的位置,_______决定圆的大小。
4.圆的特征(1)在同一个圆内,可以画______条半径,无数条______,所有的半径_________,所有的直径都相等。(2)在同一个圆内,__________________,即d=2r,半径是直径的____,即r=____d。(3)圆是轴对称图形,它有______条对称轴。
圆心
半径
无数
直径
都相等
直径是半径的2倍
无数
七.扇形和圆环
1.扇形 一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,扇形是圆的一部分。
2.圆环
___________________________________________。
同一个圆心不同半径的两个圆所组成的图形
1.3时整,时针和分针成______角,是______度;6时整,时针和分针成______角,是_________度。
2.平角=__________度,周角=__________度,1周角=_________平角=___________直角。
3.下图中,_________和___________互相平行,___________和____________互相垂直,O是__________。
即时训练
4.如下图,从A.B两点各挖一条水渠与河道想通,要是水渠最短,应该怎样挖?请你在图中画出来。如果这幅图的比例尺是 ,那么从A点挖的水渠实际长约多少米?
5.数一数,填一填。
正方形有________个;长方形有________个;圆有________个;三角形有________个。
PART 02
平面图形的周长和面积
常见平面图形的特征及周长、面积计算公式
名 称 正方形 长方形
图 形
字母意义 a—边长 a—长b —宽
特 征
周长C、面积S公式
四条边都相等,四个角都是直角
两组对边相等,四个角都是直角
C=4a S=a2
C=2(a+b) S=ab
名 称 平行四边形 三角形
图 形
字母意义 a—底h—高 a—底h—高
特 征
面积S公式
两组对边分别平行且相等
有三条边和三个角
S=ah
S= ah
名 称 梯 形 圆
图 形
字母意义 a—上底b —下底h—高 r —半径d—直径
特 征
周长C、面积S公式
只有一组对边平行
同一个圆中所有半径相等、所有直径相等,直径等于半径的2倍
C=πd=2πr S=πr2
名 称 扇 形 环 形
图 形
字母意义 r —半径 n°—圆心角度数 r —小圆半径R—大圆半径
特 征 由圆心角和圆心角所对的弧围成
面积S公式
大圆和小圆同圆心,半径不同
πr2
S= ×n
S=πR2-πr2
即时训练
1.根据圆的面积、周长公式解决问题。
计算下列图形的周长和面积。
2. 如图,大正方形的边长是10厘米,小正方形的边长是5厘米,求阴影部分的面积是多少平方厘米?
PART 03
立体图形
观察图形:
从正面看:___________观察物体得到的平面图形
____________:由上向下观察物体得到的平面图形
从左面看:___________观察物体得到的平面图形
由前向后
从上面看
由左向右
立体图形的认识
一.
1.长方体的定义
由_______________(特殊情况下有两个相对的面是正方形)围成的立体图形叫做长方体。
2.正方体的定义
由________________________围成的立体图形叫做正方体。正方体是特殊的长方体,是长、宽、高都相等的长方体。
6个长方形
6个完全相同的正方形
3.长方体和正方体的特征
名 称
图 形
展开图示例
相同点 面
棱
顶点
6个
长方体
正方体
6个
12条
12条
8个
8个
不同点 面的特点 6个面一般都是长方形,也可能有两个相对的面是正方形 6个面都是相同的正方形
面的大小
棱长 相对的棱的长度相等
联 系 正方体是特殊的长方体
相对的面的面积相等
6个面的面积都相等
棱长之和=(长+宽+高)×4=长×4+宽×4+高×4
12条棱的长度都相等棱长之和=棱长×12
二.圆柱和圆锥的定义及特征
1.圆柱的定义 以长方形的一条边所在的直线为轴旋转一周所得到的几何体叫做圆柱。
2.圆锥的定义 以直角三角形的一条直角边所在的直线为轴旋转一周得到的几何体叫做圆锥。
3.圆柱和圆锥的特征
名称 图 形 展开图示例 特 征
圆柱 上下两个底面
两个底面之间的距离
侧面展开图
长方形的长、宽、
圆柱有无数条高
圆锥 下底面
上底面缩成一点叫,
顶点到底面圆心(O)的距离
圆锥的高
圆锥的侧面展开图
1.表面积
______________________________________________。
常用的单位:平方米、平方分米、平方厘米。
2.体积
____________________________________________。
常用的单位:立方米、立方分米、立方厘米。
三 . 常见的立体图形的表面积和体积的基本概念、计算公式
物体表面面积的总和叫做物体的表面积
物体所占空间的大小叫做物体的体积
3.立体图形的表面积和体积计算公式
名称 图 形 字母意义 表(或侧)面积 体 积
正方体 a—棱长
长方体 a—长b—宽h—高
圆 柱 r —底面半径h—高C—底面周长
圆 锥 r —底面半径h—高
S表=6a2
S表=(ab+ah+bh)×2
S侧=Ch=2πrh
S表=S侧+2S底=2πrh+2πr2
V=a3
V=abh
V=S底h =πr2h
V=S底h=πr2h
即时训练
1.一个社区要挖一个长22米、宽10米、深2.5米的蓄水池.蓄水池挖好后,要在底部和四周抹一层水泥,抹水泥的面积有多大?
2.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱组成一个物体。
(1)求这个物体的体积。
(2)求这个物体的表面积。
3.一个长方体,如果长减少2厘米,就变成一个正方体,这个正方体的表面积是96平方厘米,则原来长方体的体积是________立方厘米。
4.一个圆锥与圆柱的底面积相等,已知这个圆柱与圆锥的体积比为1:6,圆锥的高是54厘米,圆柱的高是__________厘米。
5.把32升水倒入一个长8分米、宽2.5分米的长方体水箱内,正好倒满,
这个水箱深__________分米。
6.如图,这个立体图形是用棱长为1厘米的小正方体积木搭成的,
求这个立体图形的表面积、体积。
7.用两个相同的正方体拼成一个长方体,这个长方体的棱长总和是80厘米,每个正方体的表面积是多少?
8.红星小学修一条长60米、宽40米的长方形操场,先铺了10厘米厚的三合土,又铺了4厘米厚的煤渣。需要的三合土比煤渣多多少立方米?
课堂总结
谢谢观看
同课章节目录
