青岛版(五四学制)五年级下册数学比和比例(课件)(共26张PPT)
文档属性
| 名称 | 青岛版(五四学制)五年级下册数学比和比例(课件)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 16:19:09 | ||
图片预览







文档简介
(共26张PPT)
比和比例
Math courseware
比的意义和性质
求比值、化简比
正、反比例
比例的基本性质
01
02
03
04
比和比例
05
比例尺
06
应用题
PART 01
比的意义和性质
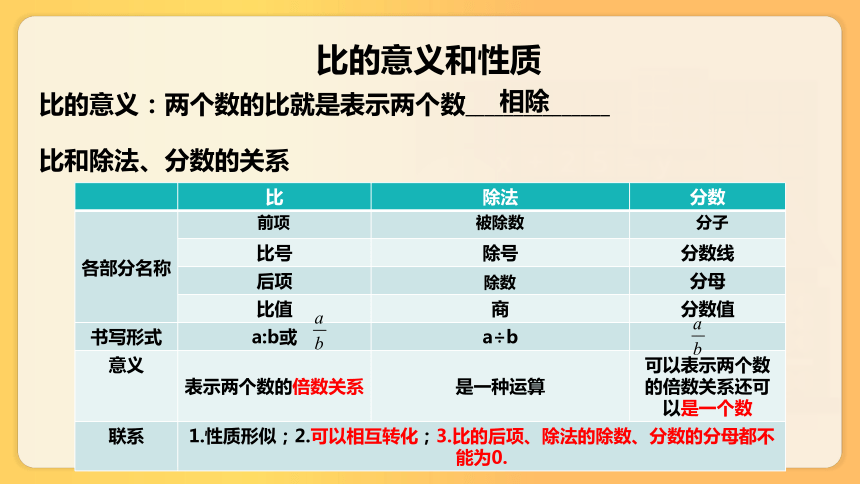
比的意义和性质
比的意义:两个数的比就是表示两个数_______________
比和除法、分数的关系
比 除法 分数
各部分名称
比号 除号 分数线
后项 分母
比值 商 分数值
书写形式 a:b或 a÷b
意义 表示两个数的倍数关系 是一种运算 可以表示两个数的倍数关系还可以是一个数
联系 1.性质形似;2.可以相互转化;3.比的后项、除法的除数、分数的分母都不能为0.
相除
分子
被除数
除数
前项
1.一杯糖水中,糖占糖水的八分之一,糖和水的比是__________
2.走同一段路,明明要用15分钟,亮亮要用12分钟,明明与亮亮走完全程所用的时间比是___________,明明与亮亮的速度比是__________
3.0.75=2.4÷______=______:12=12:_____=
1:7
5:4
4:5
3.2
9
16
1.8
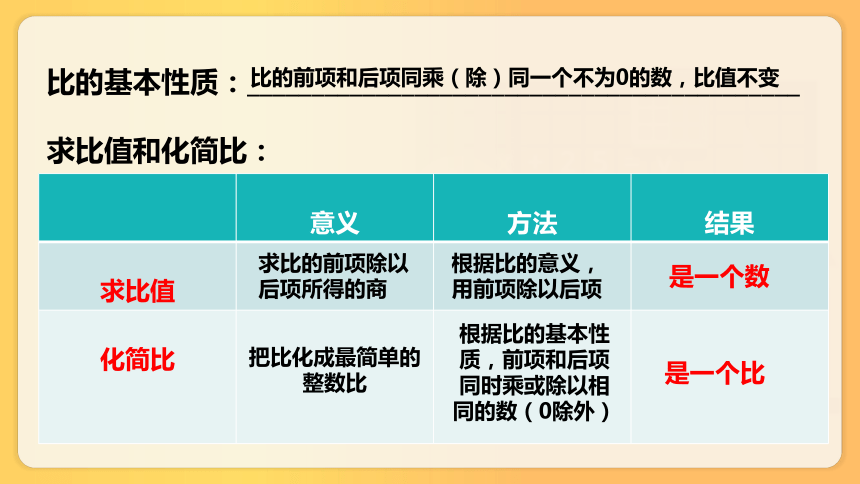
比的基本性质:___________________________________________
求比值和化简比:
意义 方法
结果
求比值
化简比 把比化成最简单的整数比
比的前项和后项同乘(除)同一个不为0的数,比值不变
求比的前项除以后项所得的商
根据比的意义,用前项除以后项
是一个数
根据比的基本性质,前项和后项同时乘或除以相同的数(0除外)
是一个比
1.把 :2的后项加上6,要是比值不变,前项应扩大______倍。
2.0.8: 的比值是______;20Kg:0.2t的比值是 _________。
3.化简比
2.7:1.8 : 1.2小时:40分
4.已知a:b=3:4,b:c=5:6,求a:b:c三个数的比。
4
PART 02
比例的基本性质
比例的意义:_____________________________________
比例的基本性质:
_________________________________________________
表示两个比相等的式子叫做比例
在一个比例中,两个外项的积等于两个內项的积。
比和比例的区别
比 比 例
意义 表示两个比相等的式子叫做比例
项数 两项:前项和后项
性质 在比例中,两个外项的积等于两个内项的积
解法
两个数相除又叫做两个数的比
四项:两个内项和两个
外项
比的前项和后项都乘(或除以)相同的数(0除外),比值不变
前项÷后项=比值
内项=外项之积÷另一个内项
外项=内项之积÷另一个外项
1,根据比例的基本性质, : =5:1可以改写成___________
2.如果a× =b × ,那么a:b=_______;如果a:b=1 ,那么
a×______=b×______.
3.判断下面的比是否可以组成比例,并把组成的比例写出来。
3:4和4.5:6 12:3和9:4.5 : 和 :
4.根据下列条件列出比例,并解答。
(1)两个外项分别是 和2.5,两个內项分别是100和0.8.求 的值。
(2)一个数与最小合数的比等于 与 的比,求这个数。
x=5y
3:5
5
6
PART 03
正比例、反比例
正比例和反比例的区别及联系
正比例 反比例
相同点
不同点 特 征
关系式
两种相关联的量,一种量变化,另一种量也随着变化
两种量相对应的两个数的比值一定
两种量相对应的两个数的积一定
=k(一定非零)
xy=k(一定、非零)
判断两种量成正比例、反比例或不成比例的方法
两种量
不是相关联的量
是相关联的量
不成比例
相关量的量的比值(商)一定
成正比例
相关量的量的积一定
成反比例
不成比例
相关量的量的积和商都不一定
1.圆的周长和半径( )
2.圆的面积和半径( )
3.正方形的周长和边长( )
4.圆柱的侧面积一定,圆柱的高和底面半径( )
5.一个非0自然数和它的倒数( )
6.比例尺一定,图上距离和实际距离( )
正、反比例的判定:
成正比例
不成比例
成正比例
成反比例
成反比例
成正比例
1.x、y、z三个相关联的量,并有xy=z.
1)当z一定时,x与y成__________比例。
2)当x一定时,z与y成__________比例。
3)当y一定时,z与y成__________比例。
2. 5x=3y,x:y=________,x和y成_____比例。
解决比和比例问题
比例尺:
图上距离和实际距离的比,叫做这幅图的比例尺。即
_______________________________________
图上距离∶实际距离=比例尺或 =比例尺
比例尺的分类:
比例尺分为________________________。
_____________,如:1∶1000000或
_____________,如:
数值比例尺和线段比例尺
数值比例尺
线段比例尺
1.设计一座房子,在平面图上用10厘米的距离表示地面上10米的距离,这幅图的比例尺为____________
2.在比例尺是1:2000000的地图上,量的两地的距离是38厘米,这两地的实际距离是_____________千米。
1.小明共买了56个气球,期中红气球和黄气球的比为4:3,红气球有___________个,黄气球有_________个.
2.一个三角形的三个内角的度数比是2:3:4,这个三角形是_______三角形。
3.小红读一本书,第一天读完后,已读的和未读的页数比是1:5,第二天读了30页,已读的的和未读的页数比变为3:5,问这本书有多少页?
应用题
4.我校食堂买来1200千克大米,6天吃了180千克,照这样计算,剩下的还能吃几天?
5.用方砖给一间教室铺地,如果同边长4分米的方砖,需要用500块。如果改用边长为5分米的方砖来铺,需方砖多少块?
6.一种农药按药粉和水1:250的比例配制而成。
(1)要配制1004克农药,需要药粉和水各多少克?
(2)现在药粉2.5千克,可以配制多少千克的农药?
7.在比例尺是1:6000000的地图上,量的两地的距离是5.5厘米,货车和客车分别从两地同时出发相向而行,2小时后相遇,货车和客车的速度比是2:3,求货车的速度。
课堂总结
比和比例
比的意义和性质
比例的基本性质
解比例、化简比、求比值
正比例、反比例
比例尺
比和比例
Math courseware
比的意义和性质
求比值、化简比
正、反比例
比例的基本性质
01
02
03
04
比和比例
05
比例尺
06
应用题
PART 01
比的意义和性质
比的意义和性质
比的意义:两个数的比就是表示两个数_______________
比和除法、分数的关系
比 除法 分数
各部分名称
比号 除号 分数线
后项 分母
比值 商 分数值
书写形式 a:b或 a÷b
意义 表示两个数的倍数关系 是一种运算 可以表示两个数的倍数关系还可以是一个数
联系 1.性质形似;2.可以相互转化;3.比的后项、除法的除数、分数的分母都不能为0.
相除
分子
被除数
除数
前项
1.一杯糖水中,糖占糖水的八分之一,糖和水的比是__________
2.走同一段路,明明要用15分钟,亮亮要用12分钟,明明与亮亮走完全程所用的时间比是___________,明明与亮亮的速度比是__________
3.0.75=2.4÷______=______:12=12:_____=
1:7
5:4
4:5
3.2
9
16
1.8
比的基本性质:___________________________________________
求比值和化简比:
意义 方法
结果
求比值
化简比 把比化成最简单的整数比
比的前项和后项同乘(除)同一个不为0的数,比值不变
求比的前项除以后项所得的商
根据比的意义,用前项除以后项
是一个数
根据比的基本性质,前项和后项同时乘或除以相同的数(0除外)
是一个比
1.把 :2的后项加上6,要是比值不变,前项应扩大______倍。
2.0.8: 的比值是______;20Kg:0.2t的比值是 _________。
3.化简比
2.7:1.8 : 1.2小时:40分
4.已知a:b=3:4,b:c=5:6,求a:b:c三个数的比。
4
PART 02
比例的基本性质
比例的意义:_____________________________________
比例的基本性质:
_________________________________________________
表示两个比相等的式子叫做比例
在一个比例中,两个外项的积等于两个內项的积。
比和比例的区别
比 比 例
意义 表示两个比相等的式子叫做比例
项数 两项:前项和后项
性质 在比例中,两个外项的积等于两个内项的积
解法
两个数相除又叫做两个数的比
四项:两个内项和两个
外项
比的前项和后项都乘(或除以)相同的数(0除外),比值不变
前项÷后项=比值
内项=外项之积÷另一个内项
外项=内项之积÷另一个外项
1,根据比例的基本性质, : =5:1可以改写成___________
2.如果a× =b × ,那么a:b=_______;如果a:b=1 ,那么
a×______=b×______.
3.判断下面的比是否可以组成比例,并把组成的比例写出来。
3:4和4.5:6 12:3和9:4.5 : 和 :
4.根据下列条件列出比例,并解答。
(1)两个外项分别是 和2.5,两个內项分别是100和0.8.求 的值。
(2)一个数与最小合数的比等于 与 的比,求这个数。
x=5y
3:5
5
6
PART 03
正比例、反比例
正比例和反比例的区别及联系
正比例 反比例
相同点
不同点 特 征
关系式
两种相关联的量,一种量变化,另一种量也随着变化
两种量相对应的两个数的比值一定
两种量相对应的两个数的积一定
=k(一定非零)
xy=k(一定、非零)
判断两种量成正比例、反比例或不成比例的方法
两种量
不是相关联的量
是相关联的量
不成比例
相关量的量的比值(商)一定
成正比例
相关量的量的积一定
成反比例
不成比例
相关量的量的积和商都不一定
1.圆的周长和半径( )
2.圆的面积和半径( )
3.正方形的周长和边长( )
4.圆柱的侧面积一定,圆柱的高和底面半径( )
5.一个非0自然数和它的倒数( )
6.比例尺一定,图上距离和实际距离( )
正、反比例的判定:
成正比例
不成比例
成正比例
成反比例
成反比例
成正比例
1.x、y、z三个相关联的量,并有xy=z.
1)当z一定时,x与y成__________比例。
2)当x一定时,z与y成__________比例。
3)当y一定时,z与y成__________比例。
2. 5x=3y,x:y=________,x和y成_____比例。
解决比和比例问题
比例尺:
图上距离和实际距离的比,叫做这幅图的比例尺。即
_______________________________________
图上距离∶实际距离=比例尺或 =比例尺
比例尺的分类:
比例尺分为________________________。
_____________,如:1∶1000000或
_____________,如:
数值比例尺和线段比例尺
数值比例尺
线段比例尺
1.设计一座房子,在平面图上用10厘米的距离表示地面上10米的距离,这幅图的比例尺为____________
2.在比例尺是1:2000000的地图上,量的两地的距离是38厘米,这两地的实际距离是_____________千米。
1.小明共买了56个气球,期中红气球和黄气球的比为4:3,红气球有___________个,黄气球有_________个.
2.一个三角形的三个内角的度数比是2:3:4,这个三角形是_______三角形。
3.小红读一本书,第一天读完后,已读的和未读的页数比是1:5,第二天读了30页,已读的的和未读的页数比变为3:5,问这本书有多少页?
应用题
4.我校食堂买来1200千克大米,6天吃了180千克,照这样计算,剩下的还能吃几天?
5.用方砖给一间教室铺地,如果同边长4分米的方砖,需要用500块。如果改用边长为5分米的方砖来铺,需方砖多少块?
6.一种农药按药粉和水1:250的比例配制而成。
(1)要配制1004克农药,需要药粉和水各多少克?
(2)现在药粉2.5千克,可以配制多少千克的农药?
7.在比例尺是1:6000000的地图上,量的两地的距离是5.5厘米,货车和客车分别从两地同时出发相向而行,2小时后相遇,货车和客车的速度比是2:3,求货车的速度。
课堂总结
比和比例
比的意义和性质
比例的基本性质
解比例、化简比、求比值
正比例、反比例
比例尺
