11.1 与三角形有关的线段 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编
文档属性
| 名称 | 11.1 与三角形有关的线段 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编 |

|
|
| 格式 | docx | ||
| 文件大小 | 765.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览



文档简介
11.1 与三角形有关的线段
一、单选题
1.(2022秋·广东韶关·八年级统考期末)如图,小明书上的三角形被墨迹遮挡了一部分,测得两个角的度数为32°、74°,于是他很快判断这个三角形是( ).
A.等边三角形 B.等腰三角形 C.直角三角形 D.钝角三角形
2.(2022秋·广东肇庆·八年级统考期末)下列长度的3根小木棒,能够搭成三角形的是( )
A.3 cm 4cm 8cm B.5 cm 6cm 7cm
C.4 cm 5cm 10cm D.5cm 7cm 12cm
3.(2022秋·广东汕头·八年级统考期末)若长度分别为2,5,的三条线段组成一个三角形,则整数的值为( )
A.2 B.3 C.4 D.7
4.(2022秋·广东广州·八年级统考期末)已知三角形的两边长分别为3cm和4cm,则该三角形第三边的长不可能是( )
A.2cm B.3cm C.5cm D.7cm
5.(2022秋·广东韶关·八年级统考期末)一个等腰三角形的两边长分别为3 cm和7 cm,则此三角形的周长为( )
A.13 cm B.17 cm C.7 cm或13 cm D.不确定
6.(2022秋·广东中山·八年级统考期末)若三角形的三边长分别是4、9、,则的取值可能是( )
A.3 B.4 C.5 D.6
7.(2022秋·广东阳江·八年级统考期末)如图,△ABC中AB边上的高是( )
A.线段AD B.线段AC C.线段CD D.线段BC
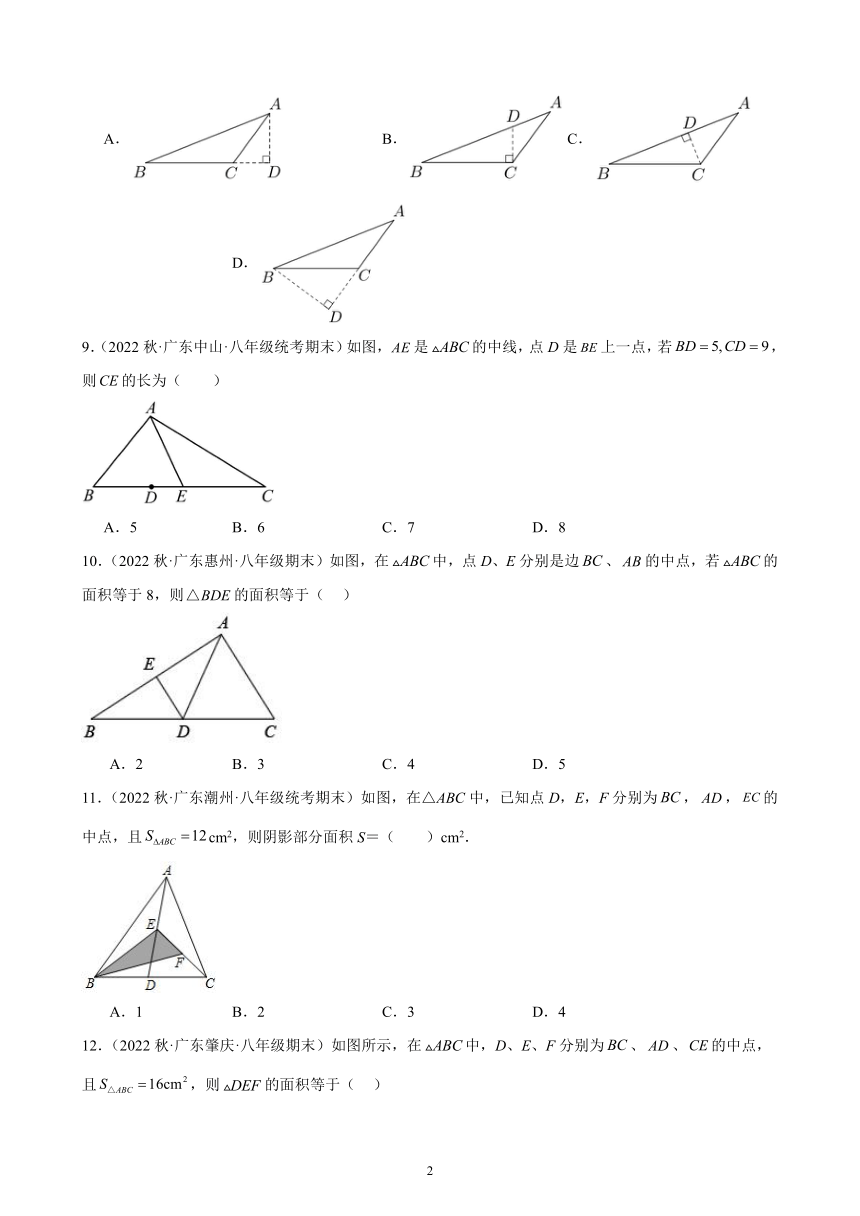
8.(2022秋·广东汕尾·八年级统考期末)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
9.(2022秋·广东中山·八年级统考期末)如图,是的中线,点D是上一点,若,则的长为( )
A.5 B.6 C.7 D.8
10.(2022秋·广东惠州·八年级期末)如图,在中,点D、E分别是边、的中点,若的面积等于8,则的面积等于( )
A.2 B.3 C.4 D.5
11.(2022秋·广东潮州·八年级统考期末)如图,在△ABC中,已知点D,E,F分别为,,的中点,且cm2,则阴影部分面积S=( )cm2.
A.1 B.2 C.3 D.4
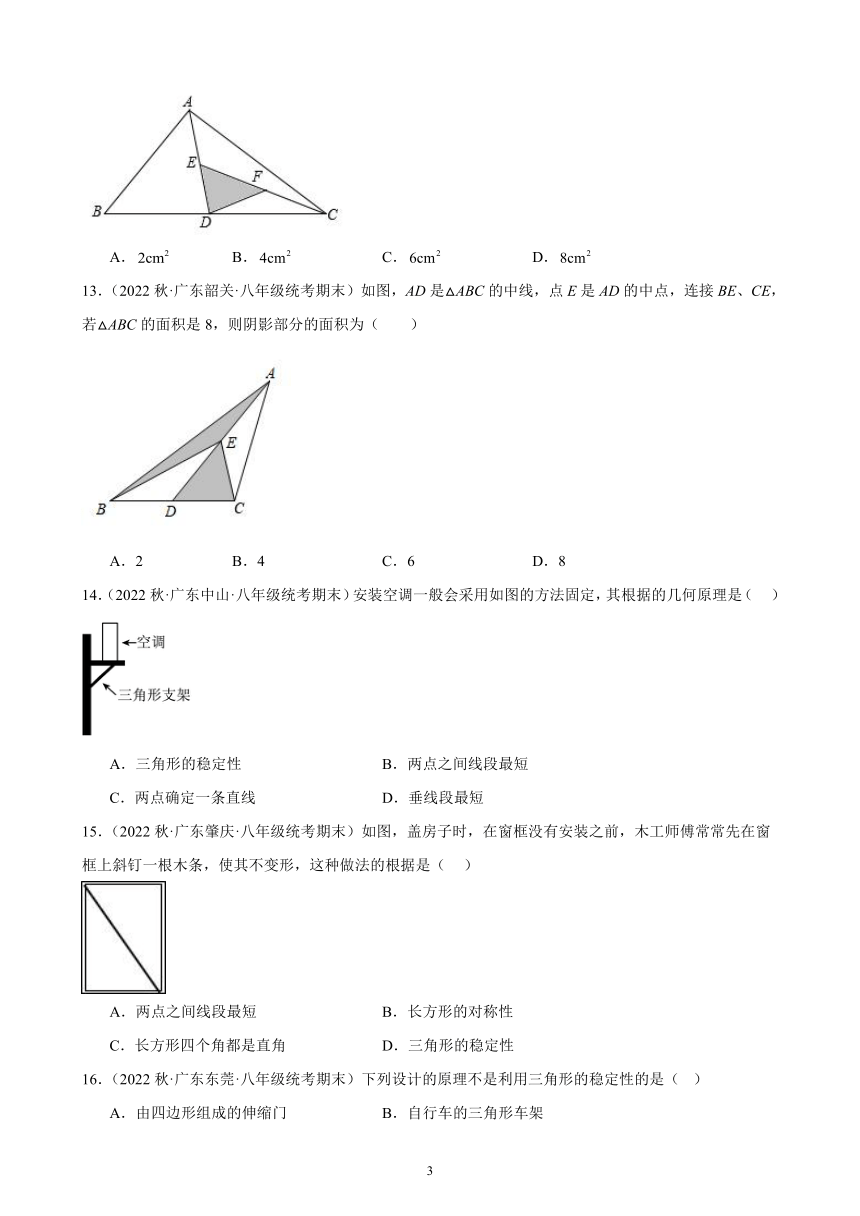
12.(2022秋·广东肇庆·八年级期末)如图所示,在中,D、E、F分别为、、的中点,且,则的面积等于( )
A. B. C. D.
13.(2022秋·广东韶关·八年级统考期末)如图,AD是△ABC的中线,点E是AD的中点,连接BE、CE,若△ABC的面积是8,则阴影部分的面积为( )
A.2 B.4 C.6 D.8
14.(2022秋·广东中山·八年级统考期末)安装空调一般会采用如图的方法固定,其根据的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
15.(2022秋·广东肇庆·八年级统考期末)如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( )
A.两点之间线段最短 B.长方形的对称性
C.长方形四个角都是直角 D.三角形的稳定性
16.(2022秋·广东东莞·八年级统考期末)下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门 B.自行车的三角形车架
C.斜钉一根木条的长方形窗框 D.照相机的三脚架
二、填空题
17.(2022秋·广东广州·八年级期末)如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为 .
18.(2022秋·广东广州·八年级统考期末)已知△ABC的面积为10,D为AC中点,则△ABD的面积为 .
19.(2022秋·广东潮州·八年级统考期末)如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2021次后得到的△A2021B2021C2021的面积为 .
20.(2022秋·广东云浮·八年级统考期末)如图,已知:分别是的边和边的中点,连接.若则的面积是 .
21.(2022秋·广东汕头·八年级统考期末)空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 .
三、解答题
22.(2022秋·广东湛江·八年级统考期末)如图,每个小正方形的边长均为1,点A和点B在小正方形的格点上.
(1)在图①中画出,使为直角三角形(要求点C在小正方形的格点上,画一个即可).
(2)求图①中的面积.
23.(2022秋·广东云浮·八年级统考期末)若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
24.(2022春·广东肇庆·八年级统考期末)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC沿着点A到点D的方向平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)画出△ABC中AB边上的高CH;(提醒:别忘了标注字母);
(2)请画出平移后的△DEF;
(3)平移后,求线段AC扫过的部分所组成的封闭图形的面积.
25.(2022春·广东惠州·八年级统考期末)如图所示,已知分别是的高和中线,.试求:
(1)的长;
(2)的面积;
(3)和的周长的差.
26.(2022秋·广东河源·八年级统考期末)如图,E,G分别是AB,AC上的点,F,D是BC上的点,连接EF,AD,DG,已知,.
(1)求证:;
(2)若DG是∠ADC的平分线,,求∠B的度数.
27.(2022春·广东揭阳·八年级统考期末)如图所示,三个顶点均在平面直角坐标系的格点上.
(1)若把向上平移2个单位长度,再向右平移2个单位长度得到,在图中画出;
(2)填空:______,______,______,的面积为______.
(3)点为轴上一点,且的面积是面积的一半,求点P的坐标.
参考答案:
1.B
【分析】根据三角形的内角和是180°,求得第三个内角的度数,然后根据角的度数判断三角形的形状.
【详解】第三个角的度数=180°-32°-74°=74°,
所以,该三角形是等腰三角形.
故选B.
【点睛】此题考查了三角形的内角和公式以及三角形的分类.
2.B
【分析】根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边判断即可.
【详解】解:A.∵3+4<8,∴不能构成三角形,故本选项不符合题意;
B.∵7﹣5<6<7+5,∴能构成三角形,故本选项符合题意;
C.∵4+5<10,∴不能构成三角形,故本选项不符合题意;
D.∵5+7=12,∴不能构成三角形,故本选项不符合题意.
故选:B.
【点睛】本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.
3.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边得到a的范围,然后再根据a是整数即可求解.
【详解】解:由三角形两边之和大于第三边,两边之差小于第三边可知:3又a为整数,
∴a可以取4、5、6,
故选:C.
【点睛】本题考查组成三角形的条件,熟练掌握“三角形两边之和大于第三边,两边之差小于第三边”的性质是解题的关键.
4.D
【分析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围即可得解.
【详解】解:设第三边长为x,则由三角形三边关系定理得4-3<x<4+3,即1<x<7.
因此,本题的第三边应满足1<x<7,把各项代入不等式不符合的即为答案.
只有7不符合不等式,
故选:D.
【点睛】考查了三角形三边关系,此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.
5.B
【分析】根据等腰三角形的定义分类讨论、再用三角形的三边关系判断,最后求周长即可;
【详解】解:①当3为底时,则7+3>7,故腰为7,则周长为7+7+3=17;
②当7为底时,则3+3<7,不能构成三角形;
故答案为B.
【点睛】本题考查了等腰三角形的概念和三角形的三边关系,掌握分类讨论思想是解答本题的关键.
6.D
【分析】根据三角形三边之间的关系即可进行解答.
【详解】解:∵三角形的三边长分别是4、9、,
∴,即,
故选:D.
【点睛】本题主要考查了三角形三边之间的关系,解题的关键是掌握三角形两边之和大于第三边,两边之差小于第三边.
7.C
【分析】根据三角形高线的定义(从三角形的一个顶点向它的对边所在的直线做垂线,顶点到垂足之间的线段叫做三角形的高线)进行判断.
【详解】解:△ABC中AB边上的高是线段CD.
故选:C.
【点睛】本题考查了三角形的高,正确理解三角形的高线的定义是解决问题关键.
8.A
【分析】经过一个顶点作对边所在的直线的垂线段,叫做三角形的高,根据概念即可得出.
【详解】根据定义可得A选项是作BC边上的高,符合题意,
B选项作的不是三角形ABC的高,不符合题意,
C选项是作AB边上的高,不符合题意,
D选项是作AC边上的高,不符合题意.
故选:A.
【点睛】本题考查三角形高线的作法,熟练掌握定义是解题关键.
9.C
【分析】先求出的长,再根据中线的定义进行求解即可.
【详解】解:∵,
∴,
∵是的中线,
∴,
故选:C.
【点睛】本题考查了线段的和差和中线的定义,熟练掌握知识点是解题的关键.
10.A
【分析】根据三角形的中线与面积公式即可得到结论.
【详解】∵点D分别是边的中点,的面积等于8,
∴,
∵点E分别是边的中点,
∴,
故选:A.
【点睛】本题考查了三角形的中线,三角形的面积的计算,解题的关键是正确的识别图形.
11.C
【分析】根据三角形面积公式由点D为的中点得到,同理得到,则,然后再由点F为的中点得到.
【详解】解:∵点D为的中点,
∴,
∵点E为的中点,
∴,
∴,
∵点F为的中点,
∴,
即阴影部分的面积为3.
故选:C.
【点睛】本题主要考查了三角形面积及三角形面积的等积变换,三角形的中线将三角形分成面积相等的两部分.
12.A
【分析】三角形的一条中线分三角形为两个三角形,这两个三角形的面积相等,根据以上内容求出每个三角形的面积,即可求出答案.
【详解】解:∵S△ABC=16cm2,D为BC中点,
∴S△ADB=S△ADC=S△ABC=8cm2,
∵E为AD的中点,
∴S△CED=S△ADC=4cm2,
∵F为CE的中点,
∴S△DEF=S△DEC=2cm2;
故选:A.
【点睛】本题考查了三角形的面积,能灵活运用等底等高的三角形的面积相等进行求解是解此题的关键.
13.B
【分析】根据三角形的中线将三角形分成面积相等的两部分的知识进行解答即可.
【详解】∵AD是△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵点E是AD的中点,
∴S△ABE=S△ADE=S△ABD,S△CDE=S△CAE=S△ACD,
∵S△ABE=S△ABC,S△CDE=S△ABC,
∴S△ABE+S△CDE=S△ABC=×8=4;
∴阴影部分的面积为4,
故选B.
【点睛】本题主要考查了三角形面积及三角形面积的等积变换,三角形的中线将三角形分成面积相等的两部分,此题难度不大.
14.A
【分析】根据三角形具有稳定性即可进行解答.
【详解】解:根据题意可得,图中的几何原理为:三角形具有稳定性;
故选:A.
【点睛】本题主要考查了三角形的性质,解题的关键是熟练掌握三角形具有稳定性.
15.D
【分析】在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木条,则分成了两个三角形,据此即可判断是利用了三角形的稳定性.
【详解】在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木条,则分成了两个三角形,利用了三角形的稳定性,D正确.
故答案选D.
【点睛】本题比较简单主要考查三角形稳定性的实际应用,通常要使一些图形具有稳定的结构,往往是将其转化为三角形而获得.
16.A
【分析】利用三角形的稳定性进行解答.
【详解】解:由四边形组成的伸缩门是利用了四边形的不稳定性,故A不是利用三角形的稳定性;
B、C、D都是利用三角形的稳定性;
故选:A.
【点睛】此题主要考查了三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
17.3
【分析】利用三角形的面积公式求出BC即可解决问题.
【详解】∵AE⊥BC,AE=4,△ABC的面积为12,
∴×BC×AE=12,
∴×BC×4=12,
∴BC=6,
∵AD是△ABC的中线,
∴CD=BC=3,
故答案为3.
【点睛】本题考查三角形的面积,三角形的中线与高等知识,解题的关键是熟练掌握基本知识,属于中基础题.
18.5
【分析】根据三角形中线的性质求解即可.
【详解】解:如图,
∵△ABC中,D为AC中点,
∴BD是AC边上的中线,
∴S△ABD=S△CBD=S△ABC=,
故答案为5.
【点睛】本题考查了三角形的中线的性质:三角形的任意一条中线将原三角形分成的两个三角形面积相等,掌握这一性质是解题的关键.
19.
【分析】根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形,然后求出第一次倍长后△A1B1C1的面积是△ABC的面积的7倍,依此规律可得结论.
【详解】解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,,
同理,
依此类推,△A2021B2021C2021的面积为=72021S△ABC,
∵△ABC的面积为1,
∴△A2021B2021C2021的面积=72021.
故答案为:72021.
【点睛】本题考查了三角形的面积,根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键.
20.6cm2
【分析】由是的中点,得中线平分的面积,同理平分的面积,从而可得答案.
【详解】解:为的中点,
为的中点,
故答案为6cm2.
【点睛】本题考查的是三角形中线把三角形的面积平分,掌握此性质是解题关键.
21.三角形的稳定性
【分析】钉在墙上的方法是构造三角形支架,因而应用了三角形的稳定性.
【详解】解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形的稳定性.
【点睛】本题考查了三角形的稳定性,正确掌握三角形的这一性质是解题的关键.
22.(1)见解析
(2)6
【分析】(1)根据直角三角形的定义画出三角形即可.(答案不唯一)
(2)根据三角形面积公式求解即可.
【详解】(1)解:如图①,△ABC即为所求.
(2)解:图①中,△ABC的面积为:ACBC=×4×3=6.
【点睛】本题考查作图-应用与设计,直角三角形的性质等知识,解题的关键是学会利用数形结合的思想解决问题.
23.(1)3<m<5;(2)19
【分析】(1)直接利用三角形三边关系得出不等式组求出答案;
(2)利用m的取值范围得出m的值,进而得出答案.
【详解】(1)根据三角形的三边关系,
,
解得:3<m<5;
(2)因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
【点睛】此题主要考查了三角形三边关系,正确得出不等式组是解题关键.
24.(1)详见解析;(2)详见解析;(3)25-9-4=12.
【分析】(1)直接利用钝角三角形高线作法得出答案;
(2)利用平移的性质得出对应点位置进而得出答案;
(3)利用平行四边形面积求法得出答案.
【详解】解:(1)如图所示:CH即为所求;
(2)如图所示:△DEF即为所求;
(3)如图,四边形ACFD的面积=S正方形BMNH-2S△BAD-2S△AHC
=52-3×3-2×2
=25-9-4
=12,
∴线段AC扫过的部分所组成的封闭图形的面积为12.
【点睛】此题主要考查了平移变换以及钝角三角形高线作法,正确得出对应点位置是解题关键.
25.(1)的长度为
(2)的面积是
(3)和的周长的差是
【分析】(1)由再代入数值即可得到答案;
(2)先求解,再利用三角形的中线的性质可得答案;
(3)利用三角形的中线的性质列式进行计算即可.
【详解】(1)解:∵是边上的高,
∴,
∵
∴,即的长度为;
(2)如图,∵是直角三角形,
∴.
又∵是边的中线,
∴,
∴,
∴.
∴的面积是.
(3)∵为边上的中线,
∴,
∴的周长的周长,
即和的周长的差是.
【点睛】本题考查的是三角形的高,中线的含义,三角形面积的计算,掌握“三角形的高,中线的含义”是解本题的关键.
26.(1)见解析
(2)35°
【分析】(1)由两直线平行,内错角相等得出,再根据题意可得出,最后根据同旁内角互补,两直线平行,即可得出;
(2)根据题意可求出的大小,再根据角平分线的定义,得出,最后根据两直线平行,同位角相等,即可求出的大小.
【详解】(1)证明:∵,
∴.
又∵,.
∴.
(2)∵,,
∴.
又∵DG是∠ADC的平分线,
∴.
∵,
∴.
【点睛】本题考查平行线的判定和性质,角平分线的定义.利用数形结合的思想是解答本题的关键.
27.(1)见解析
(2);;;6
(3)或
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点即可;
(2)利用三角形面积公式求解;
(3)设,构建方程求出m即可.
【详解】(1)解:如图,即为所求;
(2)解:∵,,,把向上平移个单位长度,再向右平移个单位长度得到,
∴,,;
的面积;
故答案为:;;;6.
(3)解:设点,则有,
∵的面积是面积的一半,
∴,
解得或,
点坐标或.
【点睛】本题考查作图一平移变换,三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
一、单选题
1.(2022秋·广东韶关·八年级统考期末)如图,小明书上的三角形被墨迹遮挡了一部分,测得两个角的度数为32°、74°,于是他很快判断这个三角形是( ).
A.等边三角形 B.等腰三角形 C.直角三角形 D.钝角三角形
2.(2022秋·广东肇庆·八年级统考期末)下列长度的3根小木棒,能够搭成三角形的是( )
A.3 cm 4cm 8cm B.5 cm 6cm 7cm
C.4 cm 5cm 10cm D.5cm 7cm 12cm
3.(2022秋·广东汕头·八年级统考期末)若长度分别为2,5,的三条线段组成一个三角形,则整数的值为( )
A.2 B.3 C.4 D.7
4.(2022秋·广东广州·八年级统考期末)已知三角形的两边长分别为3cm和4cm,则该三角形第三边的长不可能是( )
A.2cm B.3cm C.5cm D.7cm
5.(2022秋·广东韶关·八年级统考期末)一个等腰三角形的两边长分别为3 cm和7 cm,则此三角形的周长为( )
A.13 cm B.17 cm C.7 cm或13 cm D.不确定
6.(2022秋·广东中山·八年级统考期末)若三角形的三边长分别是4、9、,则的取值可能是( )
A.3 B.4 C.5 D.6
7.(2022秋·广东阳江·八年级统考期末)如图,△ABC中AB边上的高是( )
A.线段AD B.线段AC C.线段CD D.线段BC
8.(2022秋·广东汕尾·八年级统考期末)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
9.(2022秋·广东中山·八年级统考期末)如图,是的中线,点D是上一点,若,则的长为( )
A.5 B.6 C.7 D.8
10.(2022秋·广东惠州·八年级期末)如图,在中,点D、E分别是边、的中点,若的面积等于8,则的面积等于( )
A.2 B.3 C.4 D.5
11.(2022秋·广东潮州·八年级统考期末)如图,在△ABC中,已知点D,E,F分别为,,的中点,且cm2,则阴影部分面积S=( )cm2.
A.1 B.2 C.3 D.4
12.(2022秋·广东肇庆·八年级期末)如图所示,在中,D、E、F分别为、、的中点,且,则的面积等于( )
A. B. C. D.
13.(2022秋·广东韶关·八年级统考期末)如图,AD是△ABC的中线,点E是AD的中点,连接BE、CE,若△ABC的面积是8,则阴影部分的面积为( )
A.2 B.4 C.6 D.8
14.(2022秋·广东中山·八年级统考期末)安装空调一般会采用如图的方法固定,其根据的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
15.(2022秋·广东肇庆·八年级统考期末)如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( )
A.两点之间线段最短 B.长方形的对称性
C.长方形四个角都是直角 D.三角形的稳定性
16.(2022秋·广东东莞·八年级统考期末)下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门 B.自行车的三角形车架
C.斜钉一根木条的长方形窗框 D.照相机的三脚架
二、填空题
17.(2022秋·广东广州·八年级期末)如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为 .
18.(2022秋·广东广州·八年级统考期末)已知△ABC的面积为10,D为AC中点,则△ABD的面积为 .
19.(2022秋·广东潮州·八年级统考期末)如图,已知△ABC的面积为1,分别倍长(延长一倍)边AB,BC,CA得到△A1B1C1,再分别倍长边A1B1,B1C1,C1A1得到△A2B2C2…按此规律,倍长2021次后得到的△A2021B2021C2021的面积为 .
20.(2022秋·广东云浮·八年级统考期末)如图,已知:分别是的边和边的中点,连接.若则的面积是 .
21.(2022秋·广东汕头·八年级统考期末)空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 .
三、解答题
22.(2022秋·广东湛江·八年级统考期末)如图,每个小正方形的边长均为1,点A和点B在小正方形的格点上.
(1)在图①中画出,使为直角三角形(要求点C在小正方形的格点上,画一个即可).
(2)求图①中的面积.
23.(2022秋·广东云浮·八年级统考期末)若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
24.(2022春·广东肇庆·八年级统考期末)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC沿着点A到点D的方向平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)画出△ABC中AB边上的高CH;(提醒:别忘了标注字母);
(2)请画出平移后的△DEF;
(3)平移后,求线段AC扫过的部分所组成的封闭图形的面积.
25.(2022春·广东惠州·八年级统考期末)如图所示,已知分别是的高和中线,.试求:
(1)的长;
(2)的面积;
(3)和的周长的差.
26.(2022秋·广东河源·八年级统考期末)如图,E,G分别是AB,AC上的点,F,D是BC上的点,连接EF,AD,DG,已知,.
(1)求证:;
(2)若DG是∠ADC的平分线,,求∠B的度数.
27.(2022春·广东揭阳·八年级统考期末)如图所示,三个顶点均在平面直角坐标系的格点上.
(1)若把向上平移2个单位长度,再向右平移2个单位长度得到,在图中画出;
(2)填空:______,______,______,的面积为______.
(3)点为轴上一点,且的面积是面积的一半,求点P的坐标.
参考答案:
1.B
【分析】根据三角形的内角和是180°,求得第三个内角的度数,然后根据角的度数判断三角形的形状.
【详解】第三个角的度数=180°-32°-74°=74°,
所以,该三角形是等腰三角形.
故选B.
【点睛】此题考查了三角形的内角和公式以及三角形的分类.
2.B
【分析】根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边判断即可.
【详解】解:A.∵3+4<8,∴不能构成三角形,故本选项不符合题意;
B.∵7﹣5<6<7+5,∴能构成三角形,故本选项符合题意;
C.∵4+5<10,∴不能构成三角形,故本选项不符合题意;
D.∵5+7=12,∴不能构成三角形,故本选项不符合题意.
故选:B.
【点睛】本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.
3.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边得到a的范围,然后再根据a是整数即可求解.
【详解】解:由三角形两边之和大于第三边,两边之差小于第三边可知:3
∴a可以取4、5、6,
故选:C.
【点睛】本题考查组成三角形的条件,熟练掌握“三角形两边之和大于第三边,两边之差小于第三边”的性质是解题的关键.
4.D
【分析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围即可得解.
【详解】解:设第三边长为x,则由三角形三边关系定理得4-3<x<4+3,即1<x<7.
因此,本题的第三边应满足1<x<7,把各项代入不等式不符合的即为答案.
只有7不符合不等式,
故选:D.
【点睛】考查了三角形三边关系,此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.
5.B
【分析】根据等腰三角形的定义分类讨论、再用三角形的三边关系判断,最后求周长即可;
【详解】解:①当3为底时,则7+3>7,故腰为7,则周长为7+7+3=17;
②当7为底时,则3+3<7,不能构成三角形;
故答案为B.
【点睛】本题考查了等腰三角形的概念和三角形的三边关系,掌握分类讨论思想是解答本题的关键.
6.D
【分析】根据三角形三边之间的关系即可进行解答.
【详解】解:∵三角形的三边长分别是4、9、,
∴,即,
故选:D.
【点睛】本题主要考查了三角形三边之间的关系,解题的关键是掌握三角形两边之和大于第三边,两边之差小于第三边.
7.C
【分析】根据三角形高线的定义(从三角形的一个顶点向它的对边所在的直线做垂线,顶点到垂足之间的线段叫做三角形的高线)进行判断.
【详解】解:△ABC中AB边上的高是线段CD.
故选:C.
【点睛】本题考查了三角形的高,正确理解三角形的高线的定义是解决问题关键.
8.A
【分析】经过一个顶点作对边所在的直线的垂线段,叫做三角形的高,根据概念即可得出.
【详解】根据定义可得A选项是作BC边上的高,符合题意,
B选项作的不是三角形ABC的高,不符合题意,
C选项是作AB边上的高,不符合题意,
D选项是作AC边上的高,不符合题意.
故选:A.
【点睛】本题考查三角形高线的作法,熟练掌握定义是解题关键.
9.C
【分析】先求出的长,再根据中线的定义进行求解即可.
【详解】解:∵,
∴,
∵是的中线,
∴,
故选:C.
【点睛】本题考查了线段的和差和中线的定义,熟练掌握知识点是解题的关键.
10.A
【分析】根据三角形的中线与面积公式即可得到结论.
【详解】∵点D分别是边的中点,的面积等于8,
∴,
∵点E分别是边的中点,
∴,
故选:A.
【点睛】本题考查了三角形的中线,三角形的面积的计算,解题的关键是正确的识别图形.
11.C
【分析】根据三角形面积公式由点D为的中点得到,同理得到,则,然后再由点F为的中点得到.
【详解】解:∵点D为的中点,
∴,
∵点E为的中点,
∴,
∴,
∵点F为的中点,
∴,
即阴影部分的面积为3.
故选:C.
【点睛】本题主要考查了三角形面积及三角形面积的等积变换,三角形的中线将三角形分成面积相等的两部分.
12.A
【分析】三角形的一条中线分三角形为两个三角形,这两个三角形的面积相等,根据以上内容求出每个三角形的面积,即可求出答案.
【详解】解:∵S△ABC=16cm2,D为BC中点,
∴S△ADB=S△ADC=S△ABC=8cm2,
∵E为AD的中点,
∴S△CED=S△ADC=4cm2,
∵F为CE的中点,
∴S△DEF=S△DEC=2cm2;
故选:A.
【点睛】本题考查了三角形的面积,能灵活运用等底等高的三角形的面积相等进行求解是解此题的关键.
13.B
【分析】根据三角形的中线将三角形分成面积相等的两部分的知识进行解答即可.
【详解】∵AD是△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵点E是AD的中点,
∴S△ABE=S△ADE=S△ABD,S△CDE=S△CAE=S△ACD,
∵S△ABE=S△ABC,S△CDE=S△ABC,
∴S△ABE+S△CDE=S△ABC=×8=4;
∴阴影部分的面积为4,
故选B.
【点睛】本题主要考查了三角形面积及三角形面积的等积变换,三角形的中线将三角形分成面积相等的两部分,此题难度不大.
14.A
【分析】根据三角形具有稳定性即可进行解答.
【详解】解:根据题意可得,图中的几何原理为:三角形具有稳定性;
故选:A.
【点睛】本题主要考查了三角形的性质,解题的关键是熟练掌握三角形具有稳定性.
15.D
【分析】在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木条,则分成了两个三角形,据此即可判断是利用了三角形的稳定性.
【详解】在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木条,则分成了两个三角形,利用了三角形的稳定性,D正确.
故答案选D.
【点睛】本题比较简单主要考查三角形稳定性的实际应用,通常要使一些图形具有稳定的结构,往往是将其转化为三角形而获得.
16.A
【分析】利用三角形的稳定性进行解答.
【详解】解:由四边形组成的伸缩门是利用了四边形的不稳定性,故A不是利用三角形的稳定性;
B、C、D都是利用三角形的稳定性;
故选:A.
【点睛】此题主要考查了三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
17.3
【分析】利用三角形的面积公式求出BC即可解决问题.
【详解】∵AE⊥BC,AE=4,△ABC的面积为12,
∴×BC×AE=12,
∴×BC×4=12,
∴BC=6,
∵AD是△ABC的中线,
∴CD=BC=3,
故答案为3.
【点睛】本题考查三角形的面积,三角形的中线与高等知识,解题的关键是熟练掌握基本知识,属于中基础题.
18.5
【分析】根据三角形中线的性质求解即可.
【详解】解:如图,
∵△ABC中,D为AC中点,
∴BD是AC边上的中线,
∴S△ABD=S△CBD=S△ABC=,
故答案为5.
【点睛】本题考查了三角形的中线的性质:三角形的任意一条中线将原三角形分成的两个三角形面积相等,掌握这一性质是解题的关键.
19.
【分析】根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形,然后求出第一次倍长后△A1B1C1的面积是△ABC的面积的7倍,依此规律可得结论.
【详解】解:连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,,
同理,
依此类推,△A2021B2021C2021的面积为=72021S△ABC,
∵△ABC的面积为1,
∴△A2021B2021C2021的面积=72021.
故答案为:72021.
【点睛】本题考查了三角形的面积,根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键.
20.6cm2
【分析】由是的中点,得中线平分的面积,同理平分的面积,从而可得答案.
【详解】解:为的中点,
为的中点,
故答案为6cm2.
【点睛】本题考查的是三角形中线把三角形的面积平分,掌握此性质是解题关键.
21.三角形的稳定性
【分析】钉在墙上的方法是构造三角形支架,因而应用了三角形的稳定性.
【详解】解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形的稳定性.
【点睛】本题考查了三角形的稳定性,正确掌握三角形的这一性质是解题的关键.
22.(1)见解析
(2)6
【分析】(1)根据直角三角形的定义画出三角形即可.(答案不唯一)
(2)根据三角形面积公式求解即可.
【详解】(1)解:如图①,△ABC即为所求.
(2)解:图①中,△ABC的面积为:ACBC=×4×3=6.
【点睛】本题考查作图-应用与设计,直角三角形的性质等知识,解题的关键是学会利用数形结合的思想解决问题.
23.(1)3<m<5;(2)19
【分析】(1)直接利用三角形三边关系得出不等式组求出答案;
(2)利用m的取值范围得出m的值,进而得出答案.
【详解】(1)根据三角形的三边关系,
,
解得:3<m<5;
(2)因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
【点睛】此题主要考查了三角形三边关系,正确得出不等式组是解题关键.
24.(1)详见解析;(2)详见解析;(3)25-9-4=12.
【分析】(1)直接利用钝角三角形高线作法得出答案;
(2)利用平移的性质得出对应点位置进而得出答案;
(3)利用平行四边形面积求法得出答案.
【详解】解:(1)如图所示:CH即为所求;
(2)如图所示:△DEF即为所求;
(3)如图,四边形ACFD的面积=S正方形BMNH-2S△BAD-2S△AHC
=52-3×3-2×2
=25-9-4
=12,
∴线段AC扫过的部分所组成的封闭图形的面积为12.
【点睛】此题主要考查了平移变换以及钝角三角形高线作法,正确得出对应点位置是解题关键.
25.(1)的长度为
(2)的面积是
(3)和的周长的差是
【分析】(1)由再代入数值即可得到答案;
(2)先求解,再利用三角形的中线的性质可得答案;
(3)利用三角形的中线的性质列式进行计算即可.
【详解】(1)解:∵是边上的高,
∴,
∵
∴,即的长度为;
(2)如图,∵是直角三角形,
∴.
又∵是边的中线,
∴,
∴,
∴.
∴的面积是.
(3)∵为边上的中线,
∴,
∴的周长的周长,
即和的周长的差是.
【点睛】本题考查的是三角形的高,中线的含义,三角形面积的计算,掌握“三角形的高,中线的含义”是解本题的关键.
26.(1)见解析
(2)35°
【分析】(1)由两直线平行,内错角相等得出,再根据题意可得出,最后根据同旁内角互补,两直线平行,即可得出;
(2)根据题意可求出的大小,再根据角平分线的定义,得出,最后根据两直线平行,同位角相等,即可求出的大小.
【详解】(1)证明:∵,
∴.
又∵,.
∴.
(2)∵,,
∴.
又∵DG是∠ADC的平分线,
∴.
∵,
∴.
【点睛】本题考查平行线的判定和性质,角平分线的定义.利用数形结合的思想是解答本题的关键.
27.(1)见解析
(2);;;6
(3)或
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点即可;
(2)利用三角形面积公式求解;
(3)设,构建方程求出m即可.
【详解】(1)解:如图,即为所求;
(2)解:∵,,,把向上平移个单位长度,再向右平移个单位长度得到,
∴,,;
的面积;
故答案为:;;;6.
(3)解:设点,则有,
∵的面积是面积的一半,
∴,
解得或,
点坐标或.
【点睛】本题考查作图一平移变换,三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
