11.3 多边形及其内角和 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编
文档属性
| 名称 | 11.3 多边形及其内角和 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 370.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 19:37:40 | ||
图片预览




文档简介
11.3 多边形及其内角和
一、单选题
1.(2022春·广东佛山·八年级期末)过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )
A.5 B.6 C.7 D.8
2.(2022秋·广东江门·八年级统考期末)若一个多边形的内角和是,则该多边形的边数为( )
A.4 B.5 C.6 D.7
3.(2022春·广东深圳·八年级统考期末)正五边形的内角和为( )
A. B. C. D.
4.(2022秋·广东汕头·八年级统考期末)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为
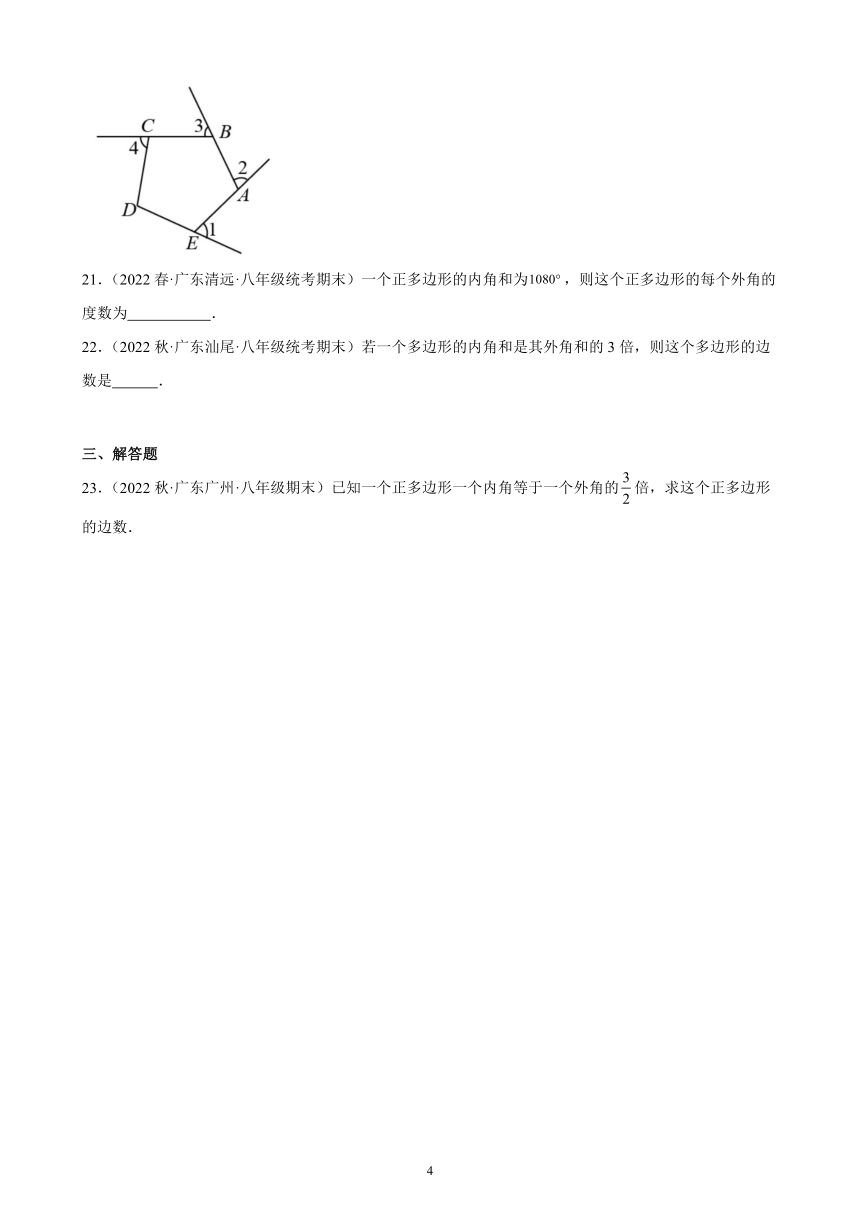
A.75° B.80° C.100° D.110°
5.(2022秋·广东中山·八年级统考期末)如图,点E在AC上,则的度数是( )
A.90° B.180° C.270° D.360°
6.(2022秋·广东潮州·八年级统考期末)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠BPC=( )
A.90°﹣α B. C.90°+α D.360°﹣α
7.(2022秋·广东江门·八年级统考期末)如图,一束平行太阳光照射到正六边形上,若,则的大小为( )
A.150° B.148° C.140° D.138°
8.(2022春·广东揭阳·八年级统考期末)若正多边形的一个外角等于45°,则这个正多边形的内角和的度数为( )
A.1080° B.1260° C.1350° D.1440°
9.(2022秋·广东广州·八年级统考期末)若一个多边形的内角和与外角和之差是,则此多边形是( )边形.
A.6 B.7 C.8 D.9
10.(2022春·广东佛山·八年级期末)用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( )
A.全等三角形 B.边长相等的正方形
C.边长相等的正三角形 D.边长相等的正五边形
二、填空题
11.(2022秋·广东惠州·八年级统考期末)若一个边形的每个内角都为,那么边数为 .
12.(2022秋·广东云浮·八年级统考期末)罗定文塔(如图)矗立于泷江曲水环抱的一个半岛上,建于明万历39年(1611年),塔高47米,建筑宏伟壮观,是罗定年代最早的高层建筑.宝塔平面可近似看成正八边形,则其每个内角的度数为 .
13.(2022秋·广东汕尾·八年级统考期末)一个多边形的内角和是,这个多边形的边数是 .
14.(2022春·广东汕尾·八年级统考期末)如图的平面图形由多条线段首尾相连构成,已知∠A=90°,则∠D+∠E+∠F+∠G= .
15.(2022秋·广东肇庆·八年级统考期末)六边形的内角和为 .
16.(2022春·广东梅州·八年级期末)一个正n多边形的一个内角是它的外角的4倍,则 .
17.(2022秋·广东云浮·八年级统考期末)如果一个正多边形的内角和是,则这个正多边形是正 边形.
18.(2022秋·广东汕头·八年级统考期末)如图1六边形的内角和为度,如图2六边形的内角和为度,则 .
19.(2022春·广东茂名·八年级统考期末)如果正多边形的一个外角为36°,那么它的边数是 .
20.(2022春·广东深圳·八年级统考期末)如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠1+∠2+∠3+∠4=290°,则∠D= .
21.(2022春·广东清远·八年级统考期末)一个正多边形的内角和为,则这个正多边形的每个外角的度数为 .
22.(2022秋·广东汕尾·八年级统考期末)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .
三、解答题
23.(2022秋·广东广州·八年级期末)已知一个正多边形一个内角等于一个外角的倍,求这个正多边形的边数.
参考答案:
1.C
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形,依此可得n的值.
【详解】解:设这个多边形的边数为n,
由题意得,n﹣2=5,
解得:n=7,
故选:C
【点睛】本题主要考查多边形的对角线,掌握多边形对角线的性质是解题的关键.
2.B
【分析】根据多边形的内角和公式列式进行计算即可求解.
【详解】解:设多边形的边数是,则
,
解得.
故选:B.
【点睛】本题主要考查了多边形的内角和公式,熟记公式是解题的关键.
3.C
【分析】根据多边形的内角和公式进行计算即可.n边形的内角和.
【详解】解:正五边形的内角和,
故选:C.
【点睛】本题主要考查了多边形的内角和,解题的关键是掌握n边形的内角和.
4.D
【分析】由题意结合三角形内角和易求出、,再根据四边形内角和即可求出的大小,最后根据对顶角相等即可求出的大小.
【详解】∵
∴,
,
在四边形CDFE中,,
∴.
故选D.
【点睛】本题考查三角形内角和定理,多边形的内角和.利用数形结合的思想是解答本题的关键.
5.B
【分析】由三角形外角的性质可得,∠AED=∠C+∠D,∠BEC=∠A+∠B,再根据平角的定义可得答案.
【详解】解:由三角形外角的性质可得,
∠AED=∠C+∠D,∠BEC=∠A+∠B,
∴∠A+∠B+∠C+∠D+∠DEB=∠AED+∠BEC+∠DEB=∠AEC=180°.
故选:B.
【点睛】本题考查多边形的内角与外角,解题的关键是熟练掌握三角形的外角的性质.
6.B
【分析】根据四边形的内角和求得,再根据角平分线的定义求得,再根据三角形内角和即可求解.
【详解】解:在四边形ABCD中,∠A+∠D=α,
∴,
由题意可得:平分,平分,
∴,,
∴,
∴
故选:B
【点睛】此题考查了多边形内角和的性质、三角形内角和的性质以及角平分线的性质,解题的关键是掌握并灵活运用相关性质进行求解.
7.B
【分析】如图,先标注各点,先求解,再证明,最后利用三角形的外角的性质可得答案.
【详解】解:如图,先标注各点,
由正六边形可得:,
∵,,
∴,
∴,
故选:B
【点睛】本题考查的是正多边形的内角和与外角和问题,平行线的性质,三角形的外角的性质,利用正多边形的外角的性质求解正多边形的每一个内角是解本题的关键.
8.A
【分析】先根据多边形的外角和定理求出多边形的边数,再根据多边形的内角和公式求出这个正多边形的内角和.
【详解】解:正多边形的边数为:360°÷45°=8,即这个多边形是正八边形,
所以该多边形的内角和为(8-2)×180°=1080°.
故选:A.
【点睛】本题主要考查了多边形的外角和定理及多边形的内角和公式,关键是掌握多边形内角和公式:(n-2) 180 (n≥3)且n为整数).
9.C
【分析】先求出多边形的内角和,再根据多边形的内角和公式求出边数即可.
【详解】解:∵一个多边形的内角和与外角和之差为720°,多边形的外角和是360°,
∴这个多边形的内角和为720°+360°=1080°,
设多边形的边数为n,
则(n-2)×180°=1080°,解得:n=8,
即多边形的边数为8,
故选:C.
【点睛】本题考查了多边形的内角和外角,能列出关于n的方程是即此题的关键,注意:边数为n的多边形的内角和=(n-2)×180°,多边形的外角和等于360°.
10.D
【分析】根据判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能判断即可.
【详解】解:A选项,三角形内角和是180°,180°×2=360°,能镶嵌,故该选项不符合题意;
B选项,正方形的每个内角是90°,90°×4=360°,能镶嵌,故该选项不符合题意;
C选项,正三角形的每个内角是60°,60°×6=360°,能镶嵌,故该选项不符合题意;
D选项,正五边形的每个内角是108°,不能镶嵌,故该选项符合题意;
故选:D.
【点睛】本题考查了平面镶嵌(密铺),掌握判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能是解题的关键.
11.12
【分析】根据多边形的内角和公式列方程求解即可.
【详解】由题意得,,
解得:.
故答案为:.
【点睛】本题考查了多边形的内角与外角,熟记内角和公式并列出方程是解题的关键.
12.
【分析】根据多边形的内角和定理求解即可.
【详解】n边形内角和,
八边形的每个内角的度数,
故答案为:.
【点睛】本题考查了多边形的内角和定理.
13.9
【分析】由多边形内角和定理:,可求多边形的边数.
【详解】解:设这个多边形的边数是n,
由题意得:,
∴,
故答案为:9.
【点睛】本题考查多边形的有关知识,关键是掌握多边形的内角和定理.
14.270°/270度
【分析】连接EF,在△AEF中,根据三角形内角和是180°得到∠AFE+∠AEF=180°-∠A=180°-90°=90°,在四边形DEFG中,根据四边形内角和是360°得到∠D+∠DEF+∠EFG+∠G=360°即可得出答案.
【详解】解:如图,连接EF,
在△AEF中,∠AFE+∠AEF=180°-∠A=180°-90°=90°,
在四边形DEFG中,∠D+∠DEF+∠EFG+∠G=360°,
∴∠D+∠DEB+∠AFG+∠G=360°-(∠AFE+∠AEF)=360°-90°=270°,
故答案为:270°.
【点睛】本题考查了多边形的内角和问题,三角形内角和定理,连接EF,构造三角形和四边形是解题的关键.
15./720度
【分析】根据多边形的内角和公式:多边形的内角和(其中为多边形的边数,且为整数),把数据代入公式解答即可.
【详解】解:∵多边形是六边形,
∴,
∴
.
∴六边形的内角和为.
故答案为:.
【点睛】本题主要考查多边形内角和公式的灵活运用,关键是熟记公式.
16.10
【分析】由多边形的每一个内角与相邻的这个外角互补先求解每一个外角,从而可得答案.
【详解】解:∵一个正n多边形的一个内角是它的外角的4倍,
∴正多边形的每一个外角为:,
∴,
故答案为:10.
【点睛】本题考查的是正多边形的内角和与外角和的综合,熟记多边形的每一个内角与相邻的这个外角互补是解本题的关键.
17.六
【分析】根据多边形的内角和公式求解即可.
【详解】设这个正多边形是正n边形,
则,
解得:.
∴这个正多边形是正六边形.
故答案为:六.
【点睛】本题考查多边形的内角和公式.掌握n边形的内角和为是解题关键.
18.0
【分析】将两个六边形分别进行拆分,再结合三角形的内角和和四边形的内角和计算即可得出答案.
【详解】如图1所示,将原六边形分成了两个三角形和一个四边形,
∴=180°×2+360°=720°
如图2所示,将原六边形分成了四个三角形
∴=180°×4=720°
∴m-n=0
故答案为0.
【点睛】本题考查的是三角形的内角和和四边形的内角和,难度适中,解题关键是将所求六边形拆分成几个三角形和四边形的形式进行求解.
19.10
【分析】根据正多边形的性质:每一个外角都相等;又根据多边形的外角和为,由此可以得出此正多边形的边数.
【详解】正多边形的一个外角为,
正多边形的每一个外角均为,
又多边形的外角和为,
正多边形的边数.
故答案为:10.
【点睛】此题考查了多边形的外角和定理与正多边形的性质.熟练运用“多边形的外角和为”与“正多边形的每一个外角均相等”是解此题的关键.
20.110°
【分析】根据多边形的外角和即可求得∠D的外角,再根据一个内角与于它相邻的外角的关系即可求解.
【详解】解:如图所示:
∵∠1+∠2+∠3+∠4=290°,
∴∠5=360°-290°=70°,
∴∠CDE=180°-70°=110°,
故答案为:110°.
【点睛】本题考查了多边形的外角和的性质,熟练掌握多边形的外角和等于360°及一个内角与于它相邻的外角互补关系是解题的关键.
21.
【分析】根据多边形的内角和公式(n 2) 180°列式进行计算求得边数,然后根据多边形的外角和即可得到结论.
【详解】解:设它是n边形,则
(n 2) 180°=1080°,
解得n=8.
360°÷8=45°,
故答案为.
【点睛】本题考查了多边形的内角和公式,熟记公式是解题的关键.
22.8
【分析】根据多边形的内角和定理,多边形的内角和等于(n﹣2) 180°,外角和等于360°,然后列方程求解即可.
【详解】解:设边数为n,由题意得,
180(n-2)=3603,
解得n=8.
所以这个多边形的边数是8.
故答案为:8.
【点睛】本题主要考查了多边形的内角和公式与外角和定理,根据题意列出方程是解题的关键.
23.5
【分析】多边形的内角和可以表示成(n-2) 180°,外角和是固定的360°,从而可根据一个正多边形的一个内角等于一个外角的列方程求解可得.
【详解】解:设此正多边形为正n边形.
∵正多边形的一个内角等于一个外角的,
∴此正多边形的内角和等于其外角和的,
∴×360°=(n-2) 180°,
解得n=5.
答:正多边形的边数为5.
【点睛】本题考查正多边形的内角和与外角和.关键是记住内角和的公式与外角和的特征.
一、单选题
1.(2022春·广东佛山·八年级期末)过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )
A.5 B.6 C.7 D.8
2.(2022秋·广东江门·八年级统考期末)若一个多边形的内角和是,则该多边形的边数为( )
A.4 B.5 C.6 D.7
3.(2022春·广东深圳·八年级统考期末)正五边形的内角和为( )
A. B. C. D.
4.(2022秋·广东汕头·八年级统考期末)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为
A.75° B.80° C.100° D.110°
5.(2022秋·广东中山·八年级统考期末)如图,点E在AC上,则的度数是( )
A.90° B.180° C.270° D.360°
6.(2022秋·广东潮州·八年级统考期末)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠BPC=( )
A.90°﹣α B. C.90°+α D.360°﹣α
7.(2022秋·广东江门·八年级统考期末)如图,一束平行太阳光照射到正六边形上,若,则的大小为( )
A.150° B.148° C.140° D.138°
8.(2022春·广东揭阳·八年级统考期末)若正多边形的一个外角等于45°,则这个正多边形的内角和的度数为( )
A.1080° B.1260° C.1350° D.1440°
9.(2022秋·广东广州·八年级统考期末)若一个多边形的内角和与外角和之差是,则此多边形是( )边形.
A.6 B.7 C.8 D.9
10.(2022春·广东佛山·八年级期末)用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( )
A.全等三角形 B.边长相等的正方形
C.边长相等的正三角形 D.边长相等的正五边形
二、填空题
11.(2022秋·广东惠州·八年级统考期末)若一个边形的每个内角都为,那么边数为 .
12.(2022秋·广东云浮·八年级统考期末)罗定文塔(如图)矗立于泷江曲水环抱的一个半岛上,建于明万历39年(1611年),塔高47米,建筑宏伟壮观,是罗定年代最早的高层建筑.宝塔平面可近似看成正八边形,则其每个内角的度数为 .
13.(2022秋·广东汕尾·八年级统考期末)一个多边形的内角和是,这个多边形的边数是 .
14.(2022春·广东汕尾·八年级统考期末)如图的平面图形由多条线段首尾相连构成,已知∠A=90°,则∠D+∠E+∠F+∠G= .
15.(2022秋·广东肇庆·八年级统考期末)六边形的内角和为 .
16.(2022春·广东梅州·八年级期末)一个正n多边形的一个内角是它的外角的4倍,则 .
17.(2022秋·广东云浮·八年级统考期末)如果一个正多边形的内角和是,则这个正多边形是正 边形.
18.(2022秋·广东汕头·八年级统考期末)如图1六边形的内角和为度,如图2六边形的内角和为度,则 .
19.(2022春·广东茂名·八年级统考期末)如果正多边形的一个外角为36°,那么它的边数是 .
20.(2022春·广东深圳·八年级统考期末)如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠1+∠2+∠3+∠4=290°,则∠D= .
21.(2022春·广东清远·八年级统考期末)一个正多边形的内角和为,则这个正多边形的每个外角的度数为 .
22.(2022秋·广东汕尾·八年级统考期末)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .
三、解答题
23.(2022秋·广东广州·八年级期末)已知一个正多边形一个内角等于一个外角的倍,求这个正多边形的边数.
参考答案:
1.C
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形,依此可得n的值.
【详解】解:设这个多边形的边数为n,
由题意得,n﹣2=5,
解得:n=7,
故选:C
【点睛】本题主要考查多边形的对角线,掌握多边形对角线的性质是解题的关键.
2.B
【分析】根据多边形的内角和公式列式进行计算即可求解.
【详解】解:设多边形的边数是,则
,
解得.
故选:B.
【点睛】本题主要考查了多边形的内角和公式,熟记公式是解题的关键.
3.C
【分析】根据多边形的内角和公式进行计算即可.n边形的内角和.
【详解】解:正五边形的内角和,
故选:C.
【点睛】本题主要考查了多边形的内角和,解题的关键是掌握n边形的内角和.
4.D
【分析】由题意结合三角形内角和易求出、,再根据四边形内角和即可求出的大小,最后根据对顶角相等即可求出的大小.
【详解】∵
∴,
,
在四边形CDFE中,,
∴.
故选D.
【点睛】本题考查三角形内角和定理,多边形的内角和.利用数形结合的思想是解答本题的关键.
5.B
【分析】由三角形外角的性质可得,∠AED=∠C+∠D,∠BEC=∠A+∠B,再根据平角的定义可得答案.
【详解】解:由三角形外角的性质可得,
∠AED=∠C+∠D,∠BEC=∠A+∠B,
∴∠A+∠B+∠C+∠D+∠DEB=∠AED+∠BEC+∠DEB=∠AEC=180°.
故选:B.
【点睛】本题考查多边形的内角与外角,解题的关键是熟练掌握三角形的外角的性质.
6.B
【分析】根据四边形的内角和求得,再根据角平分线的定义求得,再根据三角形内角和即可求解.
【详解】解:在四边形ABCD中,∠A+∠D=α,
∴,
由题意可得:平分,平分,
∴,,
∴,
∴
故选:B
【点睛】此题考查了多边形内角和的性质、三角形内角和的性质以及角平分线的性质,解题的关键是掌握并灵活运用相关性质进行求解.
7.B
【分析】如图,先标注各点,先求解,再证明,最后利用三角形的外角的性质可得答案.
【详解】解:如图,先标注各点,
由正六边形可得:,
∵,,
∴,
∴,
故选:B
【点睛】本题考查的是正多边形的内角和与外角和问题,平行线的性质,三角形的外角的性质,利用正多边形的外角的性质求解正多边形的每一个内角是解本题的关键.
8.A
【分析】先根据多边形的外角和定理求出多边形的边数,再根据多边形的内角和公式求出这个正多边形的内角和.
【详解】解:正多边形的边数为:360°÷45°=8,即这个多边形是正八边形,
所以该多边形的内角和为(8-2)×180°=1080°.
故选:A.
【点睛】本题主要考查了多边形的外角和定理及多边形的内角和公式,关键是掌握多边形内角和公式:(n-2) 180 (n≥3)且n为整数).
9.C
【分析】先求出多边形的内角和,再根据多边形的内角和公式求出边数即可.
【详解】解:∵一个多边形的内角和与外角和之差为720°,多边形的外角和是360°,
∴这个多边形的内角和为720°+360°=1080°,
设多边形的边数为n,
则(n-2)×180°=1080°,解得:n=8,
即多边形的边数为8,
故选:C.
【点睛】本题考查了多边形的内角和外角,能列出关于n的方程是即此题的关键,注意:边数为n的多边形的内角和=(n-2)×180°,多边形的外角和等于360°.
10.D
【分析】根据判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能判断即可.
【详解】解:A选项,三角形内角和是180°,180°×2=360°,能镶嵌,故该选项不符合题意;
B选项,正方形的每个内角是90°,90°×4=360°,能镶嵌,故该选项不符合题意;
C选项,正三角形的每个内角是60°,60°×6=360°,能镶嵌,故该选项不符合题意;
D选项,正五边形的每个内角是108°,不能镶嵌,故该选项符合题意;
故选:D.
【点睛】本题考查了平面镶嵌(密铺),掌握判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能是解题的关键.
11.12
【分析】根据多边形的内角和公式列方程求解即可.
【详解】由题意得,,
解得:.
故答案为:.
【点睛】本题考查了多边形的内角与外角,熟记内角和公式并列出方程是解题的关键.
12.
【分析】根据多边形的内角和定理求解即可.
【详解】n边形内角和,
八边形的每个内角的度数,
故答案为:.
【点睛】本题考查了多边形的内角和定理.
13.9
【分析】由多边形内角和定理:,可求多边形的边数.
【详解】解:设这个多边形的边数是n,
由题意得:,
∴,
故答案为:9.
【点睛】本题考查多边形的有关知识,关键是掌握多边形的内角和定理.
14.270°/270度
【分析】连接EF,在△AEF中,根据三角形内角和是180°得到∠AFE+∠AEF=180°-∠A=180°-90°=90°,在四边形DEFG中,根据四边形内角和是360°得到∠D+∠DEF+∠EFG+∠G=360°即可得出答案.
【详解】解:如图,连接EF,
在△AEF中,∠AFE+∠AEF=180°-∠A=180°-90°=90°,
在四边形DEFG中,∠D+∠DEF+∠EFG+∠G=360°,
∴∠D+∠DEB+∠AFG+∠G=360°-(∠AFE+∠AEF)=360°-90°=270°,
故答案为:270°.
【点睛】本题考查了多边形的内角和问题,三角形内角和定理,连接EF,构造三角形和四边形是解题的关键.
15./720度
【分析】根据多边形的内角和公式:多边形的内角和(其中为多边形的边数,且为整数),把数据代入公式解答即可.
【详解】解:∵多边形是六边形,
∴,
∴
.
∴六边形的内角和为.
故答案为:.
【点睛】本题主要考查多边形内角和公式的灵活运用,关键是熟记公式.
16.10
【分析】由多边形的每一个内角与相邻的这个外角互补先求解每一个外角,从而可得答案.
【详解】解:∵一个正n多边形的一个内角是它的外角的4倍,
∴正多边形的每一个外角为:,
∴,
故答案为:10.
【点睛】本题考查的是正多边形的内角和与外角和的综合,熟记多边形的每一个内角与相邻的这个外角互补是解本题的关键.
17.六
【分析】根据多边形的内角和公式求解即可.
【详解】设这个正多边形是正n边形,
则,
解得:.
∴这个正多边形是正六边形.
故答案为:六.
【点睛】本题考查多边形的内角和公式.掌握n边形的内角和为是解题关键.
18.0
【分析】将两个六边形分别进行拆分,再结合三角形的内角和和四边形的内角和计算即可得出答案.
【详解】如图1所示,将原六边形分成了两个三角形和一个四边形,
∴=180°×2+360°=720°
如图2所示,将原六边形分成了四个三角形
∴=180°×4=720°
∴m-n=0
故答案为0.
【点睛】本题考查的是三角形的内角和和四边形的内角和,难度适中,解题关键是将所求六边形拆分成几个三角形和四边形的形式进行求解.
19.10
【分析】根据正多边形的性质:每一个外角都相等;又根据多边形的外角和为,由此可以得出此正多边形的边数.
【详解】正多边形的一个外角为,
正多边形的每一个外角均为,
又多边形的外角和为,
正多边形的边数.
故答案为:10.
【点睛】此题考查了多边形的外角和定理与正多边形的性质.熟练运用“多边形的外角和为”与“正多边形的每一个外角均相等”是解此题的关键.
20.110°
【分析】根据多边形的外角和即可求得∠D的外角,再根据一个内角与于它相邻的外角的关系即可求解.
【详解】解:如图所示:
∵∠1+∠2+∠3+∠4=290°,
∴∠5=360°-290°=70°,
∴∠CDE=180°-70°=110°,
故答案为:110°.
【点睛】本题考查了多边形的外角和的性质,熟练掌握多边形的外角和等于360°及一个内角与于它相邻的外角互补关系是解题的关键.
21.
【分析】根据多边形的内角和公式(n 2) 180°列式进行计算求得边数,然后根据多边形的外角和即可得到结论.
【详解】解:设它是n边形,则
(n 2) 180°=1080°,
解得n=8.
360°÷8=45°,
故答案为.
【点睛】本题考查了多边形的内角和公式,熟记公式是解题的关键.
22.8
【分析】根据多边形的内角和定理,多边形的内角和等于(n﹣2) 180°,外角和等于360°,然后列方程求解即可.
【详解】解:设边数为n,由题意得,
180(n-2)=3603,
解得n=8.
所以这个多边形的边数是8.
故答案为:8.
【点睛】本题主要考查了多边形的内角和公式与外角和定理,根据题意列出方程是解题的关键.
23.5
【分析】多边形的内角和可以表示成(n-2) 180°,外角和是固定的360°,从而可根据一个正多边形的一个内角等于一个外角的列方程求解可得.
【详解】解:设此正多边形为正n边形.
∵正多边形的一个内角等于一个外角的,
∴此正多边形的内角和等于其外角和的,
∴×360°=(n-2) 180°,
解得n=5.
答:正多边形的边数为5.
【点睛】本题考查正多边形的内角和与外角和.关键是记住内角和的公式与外角和的特征.
