12.2 三角形全等的判定 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编
文档属性
| 名称 | 12.2 三角形全等的判定 同步练习(含解析) 2022-2023学年上学期广东省八年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 983.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 19:42:46 | ||
图片预览



文档简介
12.2 三角形全等的判定
一、单选题
1.(2022秋·广东汕尾·八年级统考期末)仔细观察用直尺和圆规作一个角等于已知角的示意图,请根据三角形全等的有关知识,说明画出的依据是( )
A. B. C. D.
2.(2022秋·广东惠州·八年级统考期末)如图,,,要使,添加条件正确的是( )
A. B.
C. D.
3.(2022秋·广东汕头·八年级统考期末)如图所示,小明试卷上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与试卷原图完全一样的三角形,那么两个三角形完全一样的依据是( )
A. B. C. D.
4.(2022秋·广东广州·八年级统考期末)如图,E是的边的中点,,连接并延长交于点D,若,则的长为( )
A.1.5 B.2 C.3 D.3.5
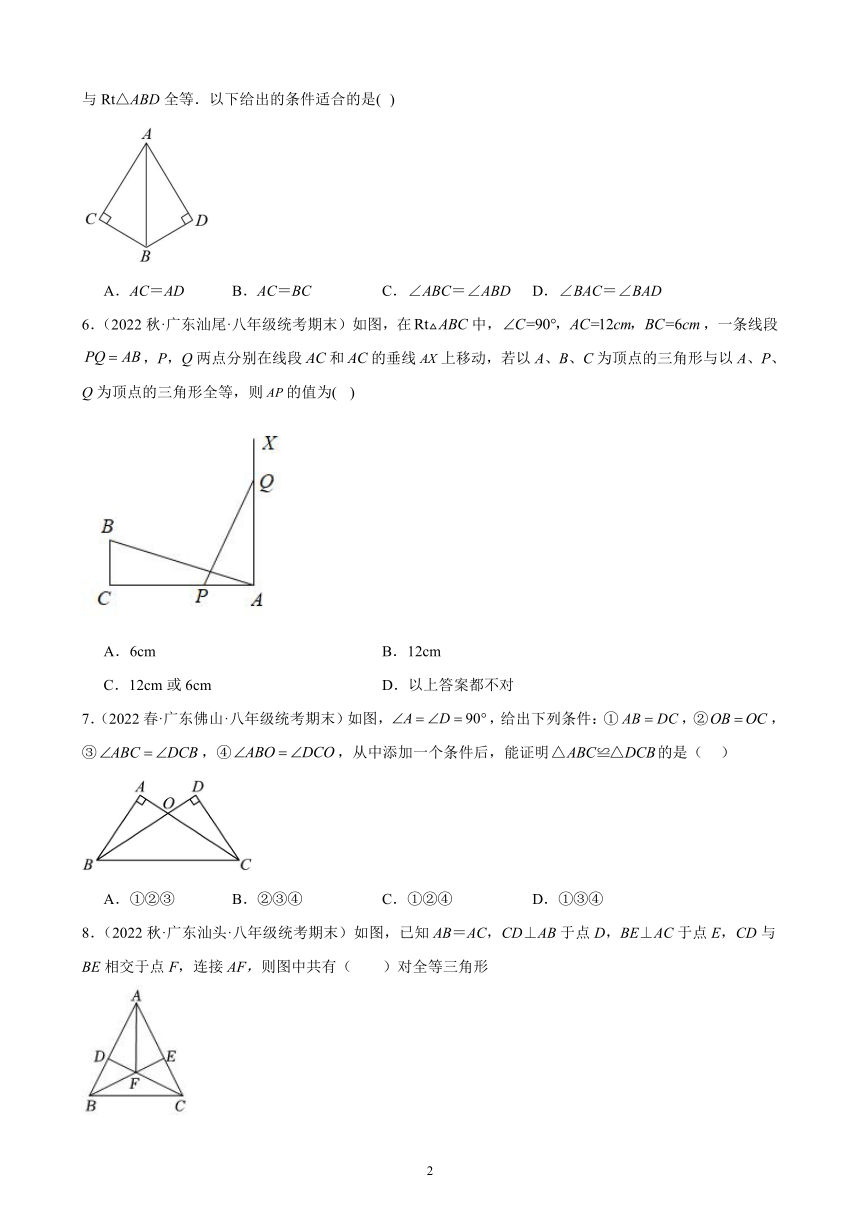
5.(2022秋·广东韶关·八年级统考期末)如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AC=BC C.∠ABC=∠ABD D.∠BAC=∠BAD
6.(2022秋·广东汕尾·八年级统考期末)如图,在中,,一条线段,P,Q两点分别在线段和的垂线上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则的值为( )
A.6cm B.12cm
C.12cm或6cm D.以上答案都不对
7.(2022春·广东佛山·八年级统考期末)如图,,给出下列条件:①,②,③,④,从中添加一个条件后,能证明的是( )
A.①②③ B.②③④ C.①②④ D.①③④
8.(2022秋·广东汕头·八年级统考期末)如图,已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD与BE相交于点F,连接AF,则图中共有( )对全等三角形
A.3 B.4 C.5 D.6
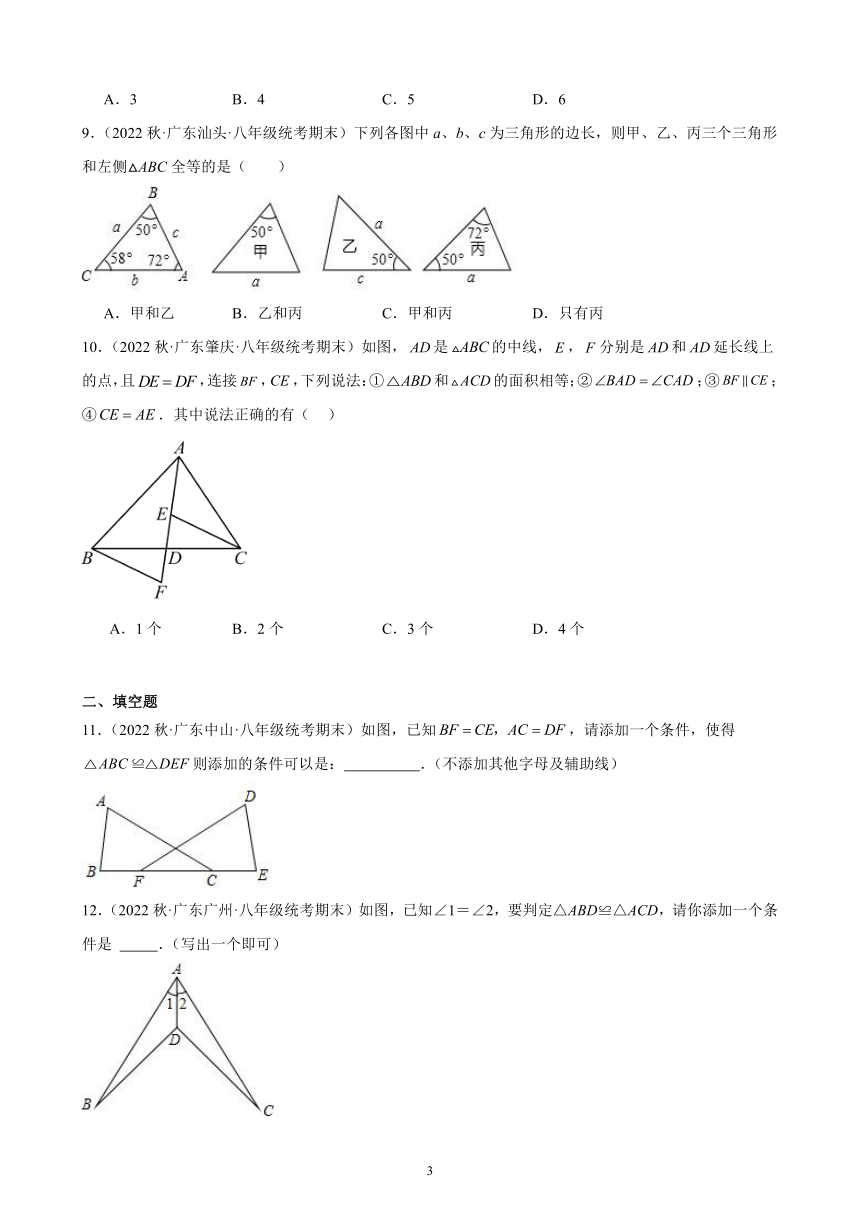
9.(2022秋·广东汕头·八年级统考期末)下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
10.(2022秋·广东肇庆·八年级统考期末)如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和的面积相等;②;③;④.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2022秋·广东中山·八年级统考期末)如图,已知,请添加一个条件,使得则添加的条件可以是: .(不添加其他字母及辅助线)
12.(2022秋·广东广州·八年级统考期末)如图,已知∠1=∠2,要判定△ABD≌△ACD,请你添加一个条件是 .(写出一个即可)
13.(2022秋·广东肇庆·八年级统考期末)如图,在中,,,,,是上一点,交于点,若,则图中阴影部分的面积为 .
14.(2022秋·广东珠海·八年级统考期末)如图,AB=CD,若要判定△ABD≌△CDB,则需要添加的一个条件是 .
15.(2022秋·广东湛江·八年级统考期末)如图,点A在线段DE上,AB⊥AC,垂足为A,且AB=AC,BD⊥DE,CE⊥DE,垂足分别为D、E,若ED=12,BD=8,则CE长为 .
16.(2022春·广东清远·八年级统考期末)如图,∠A=∠D=90°,请添加一个条件: ,使得△ABC≌△DCB.
17.(2022秋·广东广州·八年级统考期末)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 .(只需写一个,不添加辅助线)
18.(2022春·广东梅州·八年级统考期末)如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= .
三、解答题
19.(2022秋·广东云浮·八年级统考期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,,,他发现不仅平分,且平分,你觉得他的发现正确吗?请说明理由.
20.(2022秋·广东韶关·八年级统考期末)如图,点B,F,C,E在一直线上,.求证:.
21.(2022秋·广东茂名·八年级统考期末)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:;
(2)若,连接,平分,平分,求的度数.
22.(2022秋·广东云浮·八年级统考期末)如图,已知:中,为中线,且.求证:.
23.(2022秋·广东深圳·八年级统考期末)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:.
(2)若,,,求的度数.
24.(2022秋·广东江门·八年级统考期末)如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
25.(2022秋·广东肇庆·八年级统考期末)如图,点 B、F、C、E在直线l上(F、C之间不能直接测量),点 A、D在l异侧,测得, ,.求证:.
26.(2022秋·广东茂名·八年级统考期末)如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,ABCE,求∠A的度数.
27.(2022秋·广东阳江·八年级统考期末)如图,点C、E、B、F在一条直线上,于B,于E,,,求证:.
28.(2022秋·广东湛江·八年级统考期末)如图,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.
(1)求证:△OAB是等腰三角形;
(2)若∠CBA=60°,求证AC=3OC.
29.(2022春·广东揭阳·八年级统考期末)如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O,
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
30.(2022秋·广东韶关·八年级统考期末)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF.老师说:还添加一个条件就可使△ABC≌△DEF.下面是课堂上三个同学的发言:
甲:添加BE=CF,
乙:添加ACDF,
丙:添加∠A=∠D.
(1)甲、乙、丙三个同学的说法正确的是 ;
(2)请你从正确的说法中,选取一种给予证明.
31.(2022秋·广东惠州·八年级期末)如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
32.(2022秋·广东阳江·八年级统考期末)如图,已知,,连接,过点作的垂线段,使,连接.
(1)如图1,求点坐标;
(2)如图2,若点从点出发沿轴向左平移,连接,作等腰直角,连接,当点在线段上,求证:.
参考答案:
1.D
【分析】结合已知条件根据“”证明,可得答案.
【详解】解:由作法易得,,,
在与中,
,
∴,
∴(全等三角形的对应角相等).
故选:D.
【点睛】本题主要考查了作图-基本作图,全等三角形的判定与性质,灵活选择全等三角形的判定定理是正确解答本题的关键.
2.B
【分析】分别根据全等三角形的判定定理逐个判断即可.
【详解】∵,
∴,
即.
,,,不符合全等三角形的判定定理,不能推出,故A选项不符合题意;
,,,符合全等三角形的判定定理SAS,能推出,故B选项符合题意;
,,,不符合全等三角形的判定定理,不能推出,故C选项不符合题意;
,,,不符合全等三角形的判定定理.不能推出,故D选项不符合题意;
故选:B.
【点睛】本题主要考查了全等三角形的判定定理,灵活选择判定定理是解题的关键.
3.A
【分析】根据图像,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【详解】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:A.
【点睛】本题考查三角形全等的判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.
4.C
【分析】根据平行线性质得出,求出,再根据证,得,即可得出结论.
【详解】证明:∵,
∴,
∵点E为的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定与性质,平行线的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
5.A
【分析】由已知两三角形为直角三角形,且斜边为公共边,若利用HL证明两直角三角形全等,需要添加的条件为一对直角边相等,即BC=BD或AC=AD.
【详解】解: 需要添加条件为:BC= BD或AC= AD,理由为:
若添加的条件为:BC= BD
在Rt△ABC与Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL) ;
若添加的条件为:AC=AD
在Rt△ABC与Rt△ABD中,
∴Rt△ABC≌Rt△ABD( HL).
故选:A.
【点睛】本题考查了利用HL公理判定直角三角形全等,熟练运用HL公理是解题的关键
6.C
【分析】分两种情况:①当时,,②当P运动到与C点重合时,,,分别求解即可.
【详解】解:①当时,,
在与中,
,
∴,
即;
②当P运动到与C点重合时,,,
在与中,
,
∴,
即.
综上所述,或12cm.
故选:C
【点睛】本题主要考查全等三角形的判定和性质,掌握证明三角形全等,分类讨论思想方法是关键.
7.A
【分析】将条件分别代入条件中依次判断即可.
【详解】解:,
与均为直角三角形,
,,
,故①正确;
在与中,
,
,
,
,
,
,即
在与中,
,
,故②正确;
在与中,
,
,故③正确;
当时,不能推出,故④错误.
故选:A.
【点睛】本题主要考查三角形全等的判定,掌握三角形全等的判定定理是解题的关键.
8.C
【分析】由题意可直接利用“AAS”证明,得出,,.即还可利用“HL”证明,得出.从而可利用“ASA”证明,得出.进而可利用“AAS”证明,得出,最后可利用“HL”证明,由此即可选择.
【详解】由题意可知在和中,,
∴,
∴,,,
∴在和中,,
∴,
∴,即,
∴在和中,,
∴,
∴,
∴在和中,,
∴,
∴,
∴在和中,,
∴.
综上,可知图中共有5对全等三角形.
故选C.
【点睛】本题考查全等三角形的判定和性质.熟练掌握全等三角形的判定方法,证明三角形全等是解答本题的关键.
9.B
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【详解】解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选B.
【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
10.B
【分析】①和是等底同高的两个三角形,其面积相等;②注意区分中线与角平分线的性质;③由全等三角形的判定定理证得结论正确;④由③中的全等三角形的性质得到.
【详解】解:∵是的中线,
∴,
∵点A到、的距离相等,
∴和的面积相等,故①正确;
若在中,当时,不是的平分线,即,故②不一定正确;
在和中,
,
∴,
∴,
∴,故③正确;
无法证明,故④不一定正确;
综上所述,正确的有①③,共2个,
故选:B.
【点睛】本题考查了全等三角形判定和性质,解题的关键是证明.
11.AB=DE或∠ACB=∠DFE
【分析】根据全等三角形的判定定理分析即可,已知两组对应边相等,故添加的条件可以是一组对应边相等或者夹角相等,进而即可求得的答案.
【详解】解:添加的条件是AB=DE或∠ACB=∠DFE,
理由如下:∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF,
①在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
②在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
故答案为:AB=DE或∠ACB=∠DFE.
【点睛】本题考查了三角形全等的判定.解题的关键在于熟练掌握三角形全等的判定方法.
12.AB=AC或∠B=∠C或∠ADB=∠ADC
【分析】判断△ABD≌△ACD,已知的条件是:∠1=∠2,AD=AD,根据全等三角形的判定定理即可确定.
【详解】解:判断△ABD≌△ACD,已知的条件是:∠1=∠2,AD=AD,
因而根据SAS,可以添加条件:AB=AC;
根据AAS,可以添加条件:∠B=∠C;
根据ASA可以添加∠ADB=∠ADC.
故答案是:AB=AC或∠B=∠C或∠ADB=∠ADC.
【点睛】本题考查了全等三角形的判定,正确理解判定方法是关键.
13.24
【分析】证明△BAF≌△EDF(ASA),则△BAF面积等于△DEF面积,利用割补法可求得阴影部分面积.
【详解】解:∵AB∥CD,
∴∠BAD=∠D,
在△BAF和△EDF中,
,
∴△BAF≌△EDF(ASA),
∴,
∴图中阴影部分面积为,
故答案为:24.
【点睛】本题考查了全等三角形的性质和判定,平行线的性质,三角形的面积,熟练掌握全等三角形的判定是解决此题的关键.
14.∠1=∠2(或填AD=CB)
【分析】根据题意知,在△ABD与△CDB中,AB=CD,BD=DB,所以由三角形判定定理SAS可以推知,只需添加∠1=∠2即可.由三角形判定定理SSS可以推知,只需要添加AD=CB即可.
【详解】解:∵在△ABD与△CDB中,AB=CD,BD=DB,
∴添加∠1=∠2时,可以根据SAS判定△ABD≌△CDB,
添加AD=CB时,可以根据SSS判定△ABD≌△CDB,,
故答案为∠1=∠2(或填AD=CB).
【点睛】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
15.4
【分析】根据已知条件及互余关系可证△ABD≌△CAE,得出BD=AE=8,AD=CE,求出AD=4,即可得出答案.
【详解】解:∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,∠ABD+∠BAD=90°,
∵AB⊥AC,
∴∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在△ABD和△CAE中,,
∴△ABD≌△CAE(ASA),
∴BD=AE=8,AD=CE,
∴AD=ED﹣AE=12﹣8=4,
∴CE=4
故答案为:4.
【点睛】本题考查了全等三角形的判定与性质、等角的余角相等.找到证明三角形全等的条件,证明三角形全等是解题的关键.
16.∠ABC=∠DCB.
【分析】有一个直角∠A=∠D=90°相等,有一个公共边相等,可以加角,还可以加边,都行,这里我们选择加角∠ABC=∠DCB
【详解】解:因为∠A=∠D=90°,BC=CB,∠ABC=∠DCB,所以△ABC≌△DCB,故条件成立
【点睛】本题主要考查三角形全等
17.AC=DF(答案不唯一)
【详解】∵BF = CE,
∴BF+FC = CE+FC,即BC=EF;
∵AC∥DF,
∴∠ACB=∠DFE,
△ABC和△DEF中有一角一边对应相等,
∴根据全等三角形的判定,添加AC=DF,可由SAS得△ABC≌△DEF;
添加∠B=∠E,可由ASA得△ABC≌△DEF;
添加∠A=∠D,可由AAS得△ABC≌△DEF.
故答案为:AC=DF.(答案不唯一)
18.7
【详解】由MN∥PQ,AB⊥PQ,可知∠DAE=∠EBC=90°,可判定△ADE≌△BCE,从而得出AE=BC,则AB=AE+BE=AD+BC=7.
故答案为:7.
点睛:本题考查了直角三角形全等的判定和性质以及平行线的性质,是基础知识,比较简单.
19.他的发现正确,理由见解析
【分析】根据全等三角形的判定和性质直接证明即可.
【详解】解:他的发现正确,理由如下:
在与中,
,
∴,
∴,,
∴不仅平分,且平分.
【点睛】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键.
20.证明见解析
【分析】由已知条件利用等量加等量和相等证明,然后利用边角边证明,可得到,即可证得.
【详解】证明:∵,
∴,
∴,
在和中,,
∴,
∴,
∴.
【点睛】本题考查了利用边角边证明三角形全等,平行线的判定等知识点,熟练掌握以上知识点是解题的关键.
21.(1)见解析
(2)
【分析】(1)求出,根据全等三角形的性质得出,根据平行线的判定得出即可;
(2)根据(1)求出,根据三角形内角和定理求出即可.
【详解】(1)解:证明:为中点,
,
在和中,
,
,
,
;
(2)平分,
,
,
,
,,
,
.
【点睛】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点,能综合运用定理进行推理是解此题的关键.
22.见解析
【分析】由为的中线可得,进而利用可证,再利用其性质即可证明结论.
【详解】证明:∵AD是的中线
∴
∵(对顶角相等)
∴
∴.
【点睛】本题考查全等三角形的判定和性质,熟练掌握证明全等三角形的条件是解决问题的关键.
23.(1)证明见解析;
(2).
【分析】(1)求证,根据全等得出,根据平行线的判定得出即可;
(2)利用三角形外角性质求出,根据角得和差关系求出即可.
【详解】(1)证明:∵为中点,
∴,
在和中
∵
∴(SAS),
∴,
∴;
(2)由(1)知,
∴,
又∵,
∴
又∵
∴
∴.
【点睛】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形外角性质等知识点,能综合运用定理进行推理是解此题的关键.
24.(1)58°;(2)详见解析
【分析】(1)根据平行和角平分线,可推导出∠ADC=2∠G,从而得出∠ADC的大小;
(2)证△ABF≌△GCF,从而得出AB=GC,从而证AB=AD+CD.
【详解】证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
【点睛】本题考查平行的性质以及三角形全等的证明,解题关键是找出△ABF与△GCF全等的3组条件.
25.见解析
【分析】先根据得到,再根据全等三角形的判定和性质求证即可.
【详解】证明:∵,
∴,
在与中,
,
∴,
∴.
【点睛】本题考查全等三角形的判定和性质,解题的关键是掌握三角形全等的判定定理,正确寻找三角形全等所需的条件,属于基础题,中考常考题型.
26.(1)见解析
(2)120°
【分析】(1)根据“AAS”证明,即可证明;
(2)根据得到,进而证明,利用直角三角形性质得到,即可求出,,即可求出.
【详解】(1)证明:∵为的角平分线,
∴,
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,即,
∴,
即,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,直角三角形的两锐角互余,理解题意证明,进而根据平行线的性质和全等三角形性质得到是解题关键,
27.见解析
【分析】根据,得到,根据判定即可得到结论;
【详解】证明:∵,,
∴,
在和中,
,
∴,
∴,
∴,
即:.
【点睛】本题主要考查用判定直角三角形全等,解题的关键是熟练掌握直角三角形全等的判定.
28.(1)见解析;(2)见解析
【分析】(1)通过HL证明Rt△ABC≌Rt△BAD,即可得解;
(2)根据等腰三角形的性质和直角三角形的性质证明即可;
【详解】(1)证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴∠CAB=∠DBA,
∴AO=BO,
即△OAB是等腰三角形;
(2)解:由(1)得:∠CAB=∠DBA,
∴AO=BO,
∵∠CBA=60°,∠ACB=90°,
∴∠DBA=∠CAB=90°﹣∠ACB=30°,
∴∠OBC=∠CBA﹣∠DBA=30°,
∴AO=BO=2OC,
∵AC=AO+OC,
∴AC=3OC.
【点睛】本题主要考查了全等三角形的判定与性质,等腰三角形的判定与性质,直角三角形的性质,准确分析证明是解题的关键.
29.(1)见解析;(2)78°
【分析】(1)由AE=DB得出AE+EB=DB+EB,即AB=DE,利用HL即可证明Rt△ABC≌Rt△DEF;
(2)根据直角三角形的两锐角互余得∠ABC=39°,根据全等三角形的性质得∠ABC=∠DEF=39°,由三角形外角的性质即可求解.
【详解】(1)证明:∵AE=DB,
∴AE+EB=DB+EB,即AB=DE.
又∵∠C=∠F=90°,AC=DF,
∴Rt△ABC≌Rt△DEF.
(2)∵∠C=90°,∠A=51°,
∴∠ABC=∠C-∠A=90°-51°=39°.
由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∴∠DEF=39°.
∴∠BOF=∠ABC+∠BEF=39°+39°=78°.
【点睛】本题主要考查直角三角形的两锐角互余,三角形外角的性质,全等三角形的判定与性质,证明三角形全等是解题的关键.
30.(1)甲、丙
(2)选甲的做法,证明见解析
【分析】(1)通过(2),即可得出答案;
(2)利用全等三角形的判定方法:,对甲、丙两个同学的说法分别进行分析,即可得出结论.
【详解】(1)解:说法正确的是:甲、丙,
(2)选甲的做法,
证明:∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
选丙的做法,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
【点睛】本题考查了全等三角形的判定方法,解本题的关键在熟练掌握全等三角形的判定定理.
31.(1)见解析;(2)见解析;(3)∠CFE=∠CAB,见解析
【分析】(1)根据垂直的定义得到∠ACB=∠DCE=90°,由角的和差得到∠BCD=∠ACE,即可得到结论;
(2)根据全等三角形的性质得到∠CBD=∠CAE,根据对顶角的性质得到∠BGC=∠AGE,由三角形的内角和即可得到结论;
(3)过C作CH⊥AE于H,CI⊥BF于I,根据全等三角形的性质得到AE=BD,S△ACE=S△BCD,根据三角形的面积公式得到CH=CI,于是得到CF平分∠BFH,推出△ABC是等腰直角三角形,即可得到结论.
【详解】(1)证明:∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△ACE≌△BCD;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
∵△BCD≌△ACE,
∴,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。作辅助线是在几何题里常用的方法,必须学会应用。
32.(1)
(2)证明过程见详解
【分析】(1)如图所示(见详解),过点作轴于,证明,根据,,可求出,的长,由此即可求出点坐标;
(2),可知,证明,即可求证.
【详解】(1)解:如图所示,
过点作轴于,
∵,,
∴,
∴,且,
∴,且,,
∴,,
∴,.
故点坐标为:.
(2)证明:∵,
∴,
∴,
在和中,
,
∴,
∴.
【点睛】本题主要考查三角形在平面直角坐标系的变换,三角形全等的判定和性质,掌握三角形的判定和性质是解题的关键.
一、单选题
1.(2022秋·广东汕尾·八年级统考期末)仔细观察用直尺和圆规作一个角等于已知角的示意图,请根据三角形全等的有关知识,说明画出的依据是( )
A. B. C. D.
2.(2022秋·广东惠州·八年级统考期末)如图,,,要使,添加条件正确的是( )
A. B.
C. D.
3.(2022秋·广东汕头·八年级统考期末)如图所示,小明试卷上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与试卷原图完全一样的三角形,那么两个三角形完全一样的依据是( )
A. B. C. D.
4.(2022秋·广东广州·八年级统考期末)如图,E是的边的中点,,连接并延长交于点D,若,则的长为( )
A.1.5 B.2 C.3 D.3.5
5.(2022秋·广东韶关·八年级统考期末)如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AC=BC C.∠ABC=∠ABD D.∠BAC=∠BAD
6.(2022秋·广东汕尾·八年级统考期末)如图,在中,,一条线段,P,Q两点分别在线段和的垂线上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则的值为( )
A.6cm B.12cm
C.12cm或6cm D.以上答案都不对
7.(2022春·广东佛山·八年级统考期末)如图,,给出下列条件:①,②,③,④,从中添加一个条件后,能证明的是( )
A.①②③ B.②③④ C.①②④ D.①③④
8.(2022秋·广东汕头·八年级统考期末)如图,已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD与BE相交于点F,连接AF,则图中共有( )对全等三角形
A.3 B.4 C.5 D.6
9.(2022秋·广东汕头·八年级统考期末)下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
10.(2022秋·广东肇庆·八年级统考期末)如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和的面积相等;②;③;④.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2022秋·广东中山·八年级统考期末)如图,已知,请添加一个条件,使得则添加的条件可以是: .(不添加其他字母及辅助线)
12.(2022秋·广东广州·八年级统考期末)如图,已知∠1=∠2,要判定△ABD≌△ACD,请你添加一个条件是 .(写出一个即可)
13.(2022秋·广东肇庆·八年级统考期末)如图,在中,,,,,是上一点,交于点,若,则图中阴影部分的面积为 .
14.(2022秋·广东珠海·八年级统考期末)如图,AB=CD,若要判定△ABD≌△CDB,则需要添加的一个条件是 .
15.(2022秋·广东湛江·八年级统考期末)如图,点A在线段DE上,AB⊥AC,垂足为A,且AB=AC,BD⊥DE,CE⊥DE,垂足分别为D、E,若ED=12,BD=8,则CE长为 .
16.(2022春·广东清远·八年级统考期末)如图,∠A=∠D=90°,请添加一个条件: ,使得△ABC≌△DCB.
17.(2022秋·广东广州·八年级统考期末)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 .(只需写一个,不添加辅助线)
18.(2022春·广东梅州·八年级统考期末)如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= .
三、解答题
19.(2022秋·广东云浮·八年级统考期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,,,他发现不仅平分,且平分,你觉得他的发现正确吗?请说明理由.
20.(2022秋·广东韶关·八年级统考期末)如图,点B,F,C,E在一直线上,.求证:.
21.(2022秋·广东茂名·八年级统考期末)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:;
(2)若,连接,平分,平分,求的度数.
22.(2022秋·广东云浮·八年级统考期末)如图,已知:中,为中线,且.求证:.
23.(2022秋·广东深圳·八年级统考期末)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:.
(2)若,,,求的度数.
24.(2022秋·广东江门·八年级统考期末)如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
25.(2022秋·广东肇庆·八年级统考期末)如图,点 B、F、C、E在直线l上(F、C之间不能直接测量),点 A、D在l异侧,测得, ,.求证:.
26.(2022秋·广东茂名·八年级统考期末)如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,ABCE,求∠A的度数.
27.(2022秋·广东阳江·八年级统考期末)如图,点C、E、B、F在一条直线上,于B,于E,,,求证:.
28.(2022秋·广东湛江·八年级统考期末)如图,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.
(1)求证:△OAB是等腰三角形;
(2)若∠CBA=60°,求证AC=3OC.
29.(2022春·广东揭阳·八年级统考期末)如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O,
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠A=51°,求∠BOF的度数.
30.(2022秋·广东韶关·八年级统考期末)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF.老师说:还添加一个条件就可使△ABC≌△DEF.下面是课堂上三个同学的发言:
甲:添加BE=CF,
乙:添加ACDF,
丙:添加∠A=∠D.
(1)甲、乙、丙三个同学的说法正确的是 ;
(2)请你从正确的说法中,选取一种给予证明.
31.(2022秋·广东惠州·八年级期末)如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
32.(2022秋·广东阳江·八年级统考期末)如图,已知,,连接,过点作的垂线段,使,连接.
(1)如图1,求点坐标;
(2)如图2,若点从点出发沿轴向左平移,连接,作等腰直角,连接,当点在线段上,求证:.
参考答案:
1.D
【分析】结合已知条件根据“”证明,可得答案.
【详解】解:由作法易得,,,
在与中,
,
∴,
∴(全等三角形的对应角相等).
故选:D.
【点睛】本题主要考查了作图-基本作图,全等三角形的判定与性质,灵活选择全等三角形的判定定理是正确解答本题的关键.
2.B
【分析】分别根据全等三角形的判定定理逐个判断即可.
【详解】∵,
∴,
即.
,,,不符合全等三角形的判定定理,不能推出,故A选项不符合题意;
,,,符合全等三角形的判定定理SAS,能推出,故B选项符合题意;
,,,不符合全等三角形的判定定理,不能推出,故C选项不符合题意;
,,,不符合全等三角形的判定定理.不能推出,故D选项不符合题意;
故选:B.
【点睛】本题主要考查了全等三角形的判定定理,灵活选择判定定理是解题的关键.
3.A
【分析】根据图像,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出即可.
【详解】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:A.
【点睛】本题考查三角形全等的判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.
4.C
【分析】根据平行线性质得出,求出,再根据证,得,即可得出结论.
【详解】证明:∵,
∴,
∵点E为的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定与性质,平行线的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
5.A
【分析】由已知两三角形为直角三角形,且斜边为公共边,若利用HL证明两直角三角形全等,需要添加的条件为一对直角边相等,即BC=BD或AC=AD.
【详解】解: 需要添加条件为:BC= BD或AC= AD,理由为:
若添加的条件为:BC= BD
在Rt△ABC与Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL) ;
若添加的条件为:AC=AD
在Rt△ABC与Rt△ABD中,
∴Rt△ABC≌Rt△ABD( HL).
故选:A.
【点睛】本题考查了利用HL公理判定直角三角形全等,熟练运用HL公理是解题的关键
6.C
【分析】分两种情况:①当时,,②当P运动到与C点重合时,,,分别求解即可.
【详解】解:①当时,,
在与中,
,
∴,
即;
②当P运动到与C点重合时,,,
在与中,
,
∴,
即.
综上所述,或12cm.
故选:C
【点睛】本题主要考查全等三角形的判定和性质,掌握证明三角形全等,分类讨论思想方法是关键.
7.A
【分析】将条件分别代入条件中依次判断即可.
【详解】解:,
与均为直角三角形,
,,
,故①正确;
在与中,
,
,
,
,
,
,即
在与中,
,
,故②正确;
在与中,
,
,故③正确;
当时,不能推出,故④错误.
故选:A.
【点睛】本题主要考查三角形全等的判定,掌握三角形全等的判定定理是解题的关键.
8.C
【分析】由题意可直接利用“AAS”证明,得出,,.即还可利用“HL”证明,得出.从而可利用“ASA”证明,得出.进而可利用“AAS”证明,得出,最后可利用“HL”证明,由此即可选择.
【详解】由题意可知在和中,,
∴,
∴,,,
∴在和中,,
∴,
∴,即,
∴在和中,,
∴,
∴,
∴在和中,,
∴,
∴,
∴在和中,,
∴.
综上,可知图中共有5对全等三角形.
故选C.
【点睛】本题考查全等三角形的判定和性质.熟练掌握全等三角形的判定方法,证明三角形全等是解答本题的关键.
9.B
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【详解】解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选B.
【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
10.B
【分析】①和是等底同高的两个三角形,其面积相等;②注意区分中线与角平分线的性质;③由全等三角形的判定定理证得结论正确;④由③中的全等三角形的性质得到.
【详解】解:∵是的中线,
∴,
∵点A到、的距离相等,
∴和的面积相等,故①正确;
若在中,当时,不是的平分线,即,故②不一定正确;
在和中,
,
∴,
∴,
∴,故③正确;
无法证明,故④不一定正确;
综上所述,正确的有①③,共2个,
故选:B.
【点睛】本题考查了全等三角形判定和性质,解题的关键是证明.
11.AB=DE或∠ACB=∠DFE
【分析】根据全等三角形的判定定理分析即可,已知两组对应边相等,故添加的条件可以是一组对应边相等或者夹角相等,进而即可求得的答案.
【详解】解:添加的条件是AB=DE或∠ACB=∠DFE,
理由如下:∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF,
①在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
②在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
故答案为:AB=DE或∠ACB=∠DFE.
【点睛】本题考查了三角形全等的判定.解题的关键在于熟练掌握三角形全等的判定方法.
12.AB=AC或∠B=∠C或∠ADB=∠ADC
【分析】判断△ABD≌△ACD,已知的条件是:∠1=∠2,AD=AD,根据全等三角形的判定定理即可确定.
【详解】解:判断△ABD≌△ACD,已知的条件是:∠1=∠2,AD=AD,
因而根据SAS,可以添加条件:AB=AC;
根据AAS,可以添加条件:∠B=∠C;
根据ASA可以添加∠ADB=∠ADC.
故答案是:AB=AC或∠B=∠C或∠ADB=∠ADC.
【点睛】本题考查了全等三角形的判定,正确理解判定方法是关键.
13.24
【分析】证明△BAF≌△EDF(ASA),则△BAF面积等于△DEF面积,利用割补法可求得阴影部分面积.
【详解】解:∵AB∥CD,
∴∠BAD=∠D,
在△BAF和△EDF中,
,
∴△BAF≌△EDF(ASA),
∴,
∴图中阴影部分面积为,
故答案为:24.
【点睛】本题考查了全等三角形的性质和判定,平行线的性质,三角形的面积,熟练掌握全等三角形的判定是解决此题的关键.
14.∠1=∠2(或填AD=CB)
【分析】根据题意知,在△ABD与△CDB中,AB=CD,BD=DB,所以由三角形判定定理SAS可以推知,只需添加∠1=∠2即可.由三角形判定定理SSS可以推知,只需要添加AD=CB即可.
【详解】解:∵在△ABD与△CDB中,AB=CD,BD=DB,
∴添加∠1=∠2时,可以根据SAS判定△ABD≌△CDB,
添加AD=CB时,可以根据SSS判定△ABD≌△CDB,,
故答案为∠1=∠2(或填AD=CB).
【点睛】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
15.4
【分析】根据已知条件及互余关系可证△ABD≌△CAE,得出BD=AE=8,AD=CE,求出AD=4,即可得出答案.
【详解】解:∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,∠ABD+∠BAD=90°,
∵AB⊥AC,
∴∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在△ABD和△CAE中,,
∴△ABD≌△CAE(ASA),
∴BD=AE=8,AD=CE,
∴AD=ED﹣AE=12﹣8=4,
∴CE=4
故答案为:4.
【点睛】本题考查了全等三角形的判定与性质、等角的余角相等.找到证明三角形全等的条件,证明三角形全等是解题的关键.
16.∠ABC=∠DCB.
【分析】有一个直角∠A=∠D=90°相等,有一个公共边相等,可以加角,还可以加边,都行,这里我们选择加角∠ABC=∠DCB
【详解】解:因为∠A=∠D=90°,BC=CB,∠ABC=∠DCB,所以△ABC≌△DCB,故条件成立
【点睛】本题主要考查三角形全等
17.AC=DF(答案不唯一)
【详解】∵BF = CE,
∴BF+FC = CE+FC,即BC=EF;
∵AC∥DF,
∴∠ACB=∠DFE,
△ABC和△DEF中有一角一边对应相等,
∴根据全等三角形的判定,添加AC=DF,可由SAS得△ABC≌△DEF;
添加∠B=∠E,可由ASA得△ABC≌△DEF;
添加∠A=∠D,可由AAS得△ABC≌△DEF.
故答案为:AC=DF.(答案不唯一)
18.7
【详解】由MN∥PQ,AB⊥PQ,可知∠DAE=∠EBC=90°,可判定△ADE≌△BCE,从而得出AE=BC,则AB=AE+BE=AD+BC=7.
故答案为:7.
点睛:本题考查了直角三角形全等的判定和性质以及平行线的性质,是基础知识,比较简单.
19.他的发现正确,理由见解析
【分析】根据全等三角形的判定和性质直接证明即可.
【详解】解:他的发现正确,理由如下:
在与中,
,
∴,
∴,,
∴不仅平分,且平分.
【点睛】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键.
20.证明见解析
【分析】由已知条件利用等量加等量和相等证明,然后利用边角边证明,可得到,即可证得.
【详解】证明:∵,
∴,
∴,
在和中,,
∴,
∴,
∴.
【点睛】本题考查了利用边角边证明三角形全等,平行线的判定等知识点,熟练掌握以上知识点是解题的关键.
21.(1)见解析
(2)
【分析】(1)求出,根据全等三角形的性质得出,根据平行线的判定得出即可;
(2)根据(1)求出,根据三角形内角和定理求出即可.
【详解】(1)解:证明:为中点,
,
在和中,
,
,
,
;
(2)平分,
,
,
,
,,
,
.
【点睛】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点,能综合运用定理进行推理是解此题的关键.
22.见解析
【分析】由为的中线可得,进而利用可证,再利用其性质即可证明结论.
【详解】证明:∵AD是的中线
∴
∵(对顶角相等)
∴
∴.
【点睛】本题考查全等三角形的判定和性质,熟练掌握证明全等三角形的条件是解决问题的关键.
23.(1)证明见解析;
(2).
【分析】(1)求证,根据全等得出,根据平行线的判定得出即可;
(2)利用三角形外角性质求出,根据角得和差关系求出即可.
【详解】(1)证明:∵为中点,
∴,
在和中
∵
∴(SAS),
∴,
∴;
(2)由(1)知,
∴,
又∵,
∴
又∵
∴
∴.
【点睛】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形外角性质等知识点,能综合运用定理进行推理是解此题的关键.
24.(1)58°;(2)详见解析
【分析】(1)根据平行和角平分线,可推导出∠ADC=2∠G,从而得出∠ADC的大小;
(2)证△ABF≌△GCF,从而得出AB=GC,从而证AB=AD+CD.
【详解】证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
【点睛】本题考查平行的性质以及三角形全等的证明,解题关键是找出△ABF与△GCF全等的3组条件.
25.见解析
【分析】先根据得到,再根据全等三角形的判定和性质求证即可.
【详解】证明:∵,
∴,
在与中,
,
∴,
∴.
【点睛】本题考查全等三角形的判定和性质,解题的关键是掌握三角形全等的判定定理,正确寻找三角形全等所需的条件,属于基础题,中考常考题型.
26.(1)见解析
(2)120°
【分析】(1)根据“AAS”证明,即可证明;
(2)根据得到,进而证明,利用直角三角形性质得到,即可求出,,即可求出.
【详解】(1)证明:∵为的角平分线,
∴,
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,即,
∴,
即,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,直角三角形的两锐角互余,理解题意证明,进而根据平行线的性质和全等三角形性质得到是解题关键,
27.见解析
【分析】根据,得到,根据判定即可得到结论;
【详解】证明:∵,,
∴,
在和中,
,
∴,
∴,
∴,
即:.
【点睛】本题主要考查用判定直角三角形全等,解题的关键是熟练掌握直角三角形全等的判定.
28.(1)见解析;(2)见解析
【分析】(1)通过HL证明Rt△ABC≌Rt△BAD,即可得解;
(2)根据等腰三角形的性质和直角三角形的性质证明即可;
【详解】(1)证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴∠CAB=∠DBA,
∴AO=BO,
即△OAB是等腰三角形;
(2)解:由(1)得:∠CAB=∠DBA,
∴AO=BO,
∵∠CBA=60°,∠ACB=90°,
∴∠DBA=∠CAB=90°﹣∠ACB=30°,
∴∠OBC=∠CBA﹣∠DBA=30°,
∴AO=BO=2OC,
∵AC=AO+OC,
∴AC=3OC.
【点睛】本题主要考查了全等三角形的判定与性质,等腰三角形的判定与性质,直角三角形的性质,准确分析证明是解题的关键.
29.(1)见解析;(2)78°
【分析】(1)由AE=DB得出AE+EB=DB+EB,即AB=DE,利用HL即可证明Rt△ABC≌Rt△DEF;
(2)根据直角三角形的两锐角互余得∠ABC=39°,根据全等三角形的性质得∠ABC=∠DEF=39°,由三角形外角的性质即可求解.
【详解】(1)证明:∵AE=DB,
∴AE+EB=DB+EB,即AB=DE.
又∵∠C=∠F=90°,AC=DF,
∴Rt△ABC≌Rt△DEF.
(2)∵∠C=90°,∠A=51°,
∴∠ABC=∠C-∠A=90°-51°=39°.
由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∴∠DEF=39°.
∴∠BOF=∠ABC+∠BEF=39°+39°=78°.
【点睛】本题主要考查直角三角形的两锐角互余,三角形外角的性质,全等三角形的判定与性质,证明三角形全等是解题的关键.
30.(1)甲、丙
(2)选甲的做法,证明见解析
【分析】(1)通过(2),即可得出答案;
(2)利用全等三角形的判定方法:,对甲、丙两个同学的说法分别进行分析,即可得出结论.
【详解】(1)解:说法正确的是:甲、丙,
(2)选甲的做法,
证明:∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
选丙的做法,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
【点睛】本题考查了全等三角形的判定方法,解本题的关键在熟练掌握全等三角形的判定定理.
31.(1)见解析;(2)见解析;(3)∠CFE=∠CAB,见解析
【分析】(1)根据垂直的定义得到∠ACB=∠DCE=90°,由角的和差得到∠BCD=∠ACE,即可得到结论;
(2)根据全等三角形的性质得到∠CBD=∠CAE,根据对顶角的性质得到∠BGC=∠AGE,由三角形的内角和即可得到结论;
(3)过C作CH⊥AE于H,CI⊥BF于I,根据全等三角形的性质得到AE=BD,S△ACE=S△BCD,根据三角形的面积公式得到CH=CI,于是得到CF平分∠BFH,推出△ABC是等腰直角三角形,即可得到结论.
【详解】(1)证明:∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△ACE≌△BCD;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
∵△BCD≌△ACE,
∴,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。作辅助线是在几何题里常用的方法,必须学会应用。
32.(1)
(2)证明过程见详解
【分析】(1)如图所示(见详解),过点作轴于,证明,根据,,可求出,的长,由此即可求出点坐标;
(2),可知,证明,即可求证.
【详解】(1)解:如图所示,
过点作轴于,
∵,,
∴,
∴,且,
∴,且,,
∴,,
∴,.
故点坐标为:.
(2)证明:∵,
∴,
∴,
在和中,
,
∴,
∴.
【点睛】本题主要考查三角形在平面直角坐标系的变换,三角形全等的判定和性质,掌握三角形的判定和性质是解题的关键.
