鲁教版(五四学制)数学 六年级上册第2.1 有理数 课件(共31张PPT)
文档属性
| 名称 | 鲁教版(五四学制)数学 六年级上册第2.1 有理数 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 20:43:21 | ||
图片预览











文档简介
(共31张PPT)
有 理 数
月球表面白天气温可高达123℃,夜晚可低至-233℃. 图中阿波罗11号的宇航员登上月球后不得不穿着既防寒又御热的太空服。
1、你知道上面123℃和-233℃这两个量分别表示什么吗?
2、你还在哪些地方见到过用带“-”号的数来表示某一种量?
情景导入
我们在小学数学里学过那些数?
这些数能满足我们生活的需要吗?
还会有新的数吗?
想一想 议一议
1.在具体情景中,进一步认识负数,理解有理数的意义。
2.经历用正负数表示具有相反意义的量的过程,体会引
入负数是实际生活的需要。
3.会判断一个数是正数还是负数,能按一定的标准对有
理数进行分类。
学习目标
二、探索新知
某班举行知识竞赛,评分标准是:答对一题加1分,
答错一题扣1分,不回答得0分;每个队的基本分均为0
分.两个代表队答题情况如下表:
答对
答错
不回答
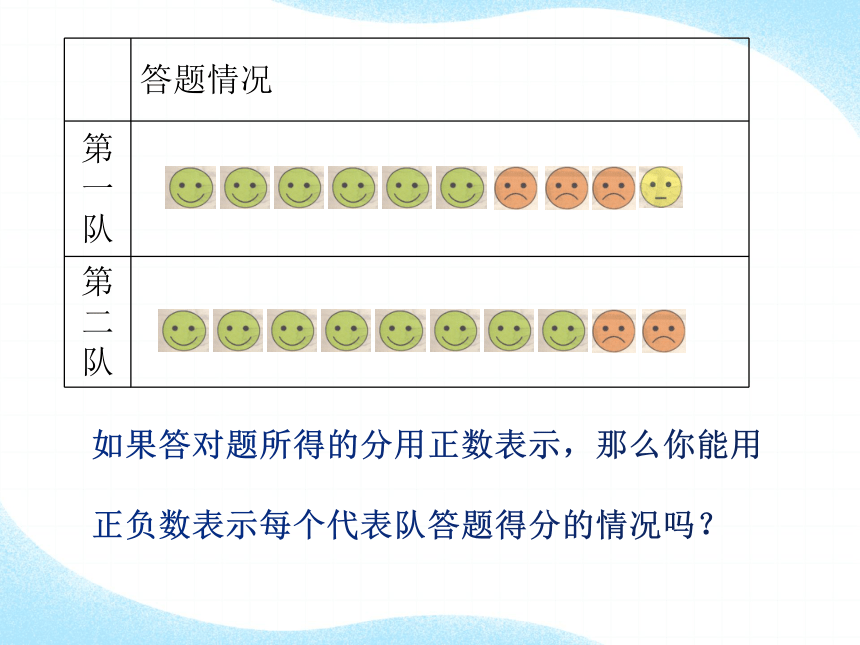
答题情况
第一队
第二队
如果答对题所得的分用正数表示,那么你能用
正负数表示每个代表队答题得分的情况吗?
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2 0
-3
0
+8
预习诊断
1.用正负数表示下列具有相反意义的量:
(1)高于海平面3m记为+3m,则低于海平面88m,记为 。
(2)如果向南走5km记为-5km,那么向北走10km记为 。
2.如果粮食增产500吨记作+500吨,那么-500吨表示什么意义 。
具有相反意义的量
正数 负数
(1)相反意义的量是成对出现的,单独一个量不成为相反意
义的量。
(2)与一个量成相反意义的量不止一个,如与上升2m
成相反意义的量就很多,如:下降1m,下降0.2m
(3)相反意义的量包含两个要素:一是它们的意义要相
反;二是它们都具有数量。如前进8m与前进5m,上升与
下降都不是相反意义的量;因为前者意义相同,后者缺
少数量。
怎么样理解相反意义的量
(4)意义相反的量中的两个量必须是同类量,如节约汽油
3吨与浪费1吨水就不是具有相反意义的量。
(5)对于两个具有相反意义的量,把哪一种意义规定为
正,带有任意性,不过习惯上把上升、增加、收入、
零上等规定为正,而把与它们意义相反的量规定为负。
具有相反意义的量的含义:
注意:
一是两个量,数字部分不一定相等;
二是必须要具有相反的意义。
缺一不可
+6
-3
0
+8
-2
0
0既不是正数,也不是负数。
(1)下列各组量中,不是具有相反意义的量是( )
A、向南走100米和向北走50米 B、零上10℃和零下2℃
C、赢了10局和输了5局 D、伸长10厘米和减少3千克
(2)规定向北为正,某人走了+5千米后,又继续走了-10千米,
那么它实际上( )
A、向北走了15千米 B、向南走了15千米
C、向北走了5千米 D、向南走了5千米
跟踪练习
(3)如果高于海平面105米记作+105米,那么低于海平面102米 记作_______。
(4)如果上升10米记作+10米,那么下降12米记作________。
(5)转动转盘,用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?
(6)在乒乓球质量检测中,一只乒乓球超出标准质量0.02kg记
+0.02kg,那么-0.03kg表示什么?
(7)大米包装袋上标注“净含量:10kg 150g”,这里的“10kg 150g”表示什么?
思考:1.问题(3)(4)的基准分别是什么?
2.所有的基数都必须是0吗?
3.问题(7)中100kg 150g表示什么意思?
差缺补漏
某方便面厂生产的100g袋装方便面的外包装上印有(100 5)g
①请问100 5g表示什么意义?
②某同学购买了一袋这样的方便面,称了一下发现只有97g,问该厂家是否有欺诈行为?
总结一下到现在为止你学习了哪些数?
1,2 ,3 ,4 ,5……
整数
0
加上
自然数
-1,-2 ,-3 ,-4 ,-5……
负整数
正整数
整数
正整数
0
负整数
负分数
正分数
分数
-
-
有理数的分类
我们把正整数、0和负整数统称为整数;如2是整数,而且是正整数,-2是负整数;
正分数和负分数统称为分数。2/3是分数,而且是正分数,-2/3是负分数。
整数和分数统称为有理数。
整数
正整数
零
负整数
负分数
分数
有理数
正分数
整数与分数统称为有理数
按定义分类:
3,无限不循环小数不是有理数;(如 等)不是分数(无理数)
有理数分类的几点注意:
1,如 能约分成整数的数________(填“能”或“不能”)算做分数;
2,两个整数的比(如 等)、有限小数(如0.2,
-3.14等)、无限循环小数(如 等)都是分数;
不能
4,整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
注意:①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
零
按性质分类:
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
(5)一个有理数非负即正( )
(6)一个有理数不是整数就是分数( )
(7)有理数是自然数和负数的统称( )
(8)有理数是整数、分数、正有理数、负
有理数、和零的统称。( )
巩固练习
√
×
√
×
×
√
×
×
1、正整数_________和____统称整数。________和________统称
为分数。
2、_______和_______统称为有理数。
3.甲地的海拔-22m,乙地海拔-18m,则____地比____地要高
些。
4.若a是负数,则-a是_____数,若-a是负数,则a是______数。
负整数
0
正分数
负分数
分数
整数
甲
乙
正
正
5.下列说法错误的是( )
A .负整数和负分数统称负有理数
B.正整数、0、负整数统称为整数
C.正有理数与负有理数组成全体有理数
D.3.14是小数,也是分数
C
6.下列说法正确的是 ( )
A.0既不是正数,也不是负数,也不是整数
B.正整数与负整数统称为整数
C.-3.14既是分数,也是负数,也是有理数
D.0是最小的有理数
C
7.下列说法中正确的个数有( )
①-3是负分数;
②2.4不是整数;
③非负有理数不包括零;
④正整数、负整数统称为整数;
⑤0是最小的有理数。
A.1个 B.2个 C.3个 D.4个
A
8.下列说法正确的个数为( )
①0是整数
②负分数一定是负有理数
③一个数不是正数就是负数
④π是有理数
A.0个 B.2个 C.3个 D.1个
B
反思小结
用一句话“我知道了……我学会了……我还想知道……”小结本课。
有 理 数
月球表面白天气温可高达123℃,夜晚可低至-233℃. 图中阿波罗11号的宇航员登上月球后不得不穿着既防寒又御热的太空服。
1、你知道上面123℃和-233℃这两个量分别表示什么吗?
2、你还在哪些地方见到过用带“-”号的数来表示某一种量?
情景导入
我们在小学数学里学过那些数?
这些数能满足我们生活的需要吗?
还会有新的数吗?
想一想 议一议
1.在具体情景中,进一步认识负数,理解有理数的意义。
2.经历用正负数表示具有相反意义的量的过程,体会引
入负数是实际生活的需要。
3.会判断一个数是正数还是负数,能按一定的标准对有
理数进行分类。
学习目标
二、探索新知
某班举行知识竞赛,评分标准是:答对一题加1分,
答错一题扣1分,不回答得0分;每个队的基本分均为0
分.两个代表队答题情况如下表:
答对
答错
不回答
答题情况
第一队
第二队
如果答对题所得的分用正数表示,那么你能用
正负数表示每个代表队答题得分的情况吗?
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2 0
-3
0
+8
预习诊断
1.用正负数表示下列具有相反意义的量:
(1)高于海平面3m记为+3m,则低于海平面88m,记为 。
(2)如果向南走5km记为-5km,那么向北走10km记为 。
2.如果粮食增产500吨记作+500吨,那么-500吨表示什么意义 。
具有相反意义的量
正数 负数
(1)相反意义的量是成对出现的,单独一个量不成为相反意
义的量。
(2)与一个量成相反意义的量不止一个,如与上升2m
成相反意义的量就很多,如:下降1m,下降0.2m
(3)相反意义的量包含两个要素:一是它们的意义要相
反;二是它们都具有数量。如前进8m与前进5m,上升与
下降都不是相反意义的量;因为前者意义相同,后者缺
少数量。
怎么样理解相反意义的量
(4)意义相反的量中的两个量必须是同类量,如节约汽油
3吨与浪费1吨水就不是具有相反意义的量。
(5)对于两个具有相反意义的量,把哪一种意义规定为
正,带有任意性,不过习惯上把上升、增加、收入、
零上等规定为正,而把与它们意义相反的量规定为负。
具有相反意义的量的含义:
注意:
一是两个量,数字部分不一定相等;
二是必须要具有相反的意义。
缺一不可
+6
-3
0
+8
-2
0
0既不是正数,也不是负数。
(1)下列各组量中,不是具有相反意义的量是( )
A、向南走100米和向北走50米 B、零上10℃和零下2℃
C、赢了10局和输了5局 D、伸长10厘米和减少3千克
(2)规定向北为正,某人走了+5千米后,又继续走了-10千米,
那么它实际上( )
A、向北走了15千米 B、向南走了15千米
C、向北走了5千米 D、向南走了5千米
跟踪练习
(3)如果高于海平面105米记作+105米,那么低于海平面102米 记作_______。
(4)如果上升10米记作+10米,那么下降12米记作________。
(5)转动转盘,用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?
(6)在乒乓球质量检测中,一只乒乓球超出标准质量0.02kg记
+0.02kg,那么-0.03kg表示什么?
(7)大米包装袋上标注“净含量:10kg 150g”,这里的“10kg 150g”表示什么?
思考:1.问题(3)(4)的基准分别是什么?
2.所有的基数都必须是0吗?
3.问题(7)中100kg 150g表示什么意思?
差缺补漏
某方便面厂生产的100g袋装方便面的外包装上印有(100 5)g
①请问100 5g表示什么意义?
②某同学购买了一袋这样的方便面,称了一下发现只有97g,问该厂家是否有欺诈行为?
总结一下到现在为止你学习了哪些数?
1,2 ,3 ,4 ,5……
整数
0
加上
自然数
-1,-2 ,-3 ,-4 ,-5……
负整数
正整数
整数
正整数
0
负整数
负分数
正分数
分数
-
-
有理数的分类
我们把正整数、0和负整数统称为整数;如2是整数,而且是正整数,-2是负整数;
正分数和负分数统称为分数。2/3是分数,而且是正分数,-2/3是负分数。
整数和分数统称为有理数。
整数
正整数
零
负整数
负分数
分数
有理数
正分数
整数与分数统称为有理数
按定义分类:
3,无限不循环小数不是有理数;(如 等)不是分数(无理数)
有理数分类的几点注意:
1,如 能约分成整数的数________(填“能”或“不能”)算做分数;
2,两个整数的比(如 等)、有限小数(如0.2,
-3.14等)、无限循环小数(如 等)都是分数;
不能
4,整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
注意:①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
零
按性质分类:
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
(5)一个有理数非负即正( )
(6)一个有理数不是整数就是分数( )
(7)有理数是自然数和负数的统称( )
(8)有理数是整数、分数、正有理数、负
有理数、和零的统称。( )
巩固练习
√
×
√
×
×
√
×
×
1、正整数_________和____统称整数。________和________统称
为分数。
2、_______和_______统称为有理数。
3.甲地的海拔-22m,乙地海拔-18m,则____地比____地要高
些。
4.若a是负数,则-a是_____数,若-a是负数,则a是______数。
负整数
0
正分数
负分数
分数
整数
甲
乙
正
正
5.下列说法错误的是( )
A .负整数和负分数统称负有理数
B.正整数、0、负整数统称为整数
C.正有理数与负有理数组成全体有理数
D.3.14是小数,也是分数
C
6.下列说法正确的是 ( )
A.0既不是正数,也不是负数,也不是整数
B.正整数与负整数统称为整数
C.-3.14既是分数,也是负数,也是有理数
D.0是最小的有理数
C
7.下列说法中正确的个数有( )
①-3是负分数;
②2.4不是整数;
③非负有理数不包括零;
④正整数、负整数统称为整数;
⑤0是最小的有理数。
A.1个 B.2个 C.3个 D.4个
A
8.下列说法正确的个数为( )
①0是整数
②负分数一定是负有理数
③一个数不是正数就是负数
④π是有理数
A.0个 B.2个 C.3个 D.1个
B
反思小结
用一句话“我知道了……我学会了……我还想知道……”小结本课。
