人教版九年级数学上册21.2.2公式法 学习任务单(公开课2课时导学案)(含部分答案)
文档属性
| 名称 | 人教版九年级数学上册21.2.2公式法 学习任务单(公开课2课时导学案)(含部分答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 378.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 22:11:09 | ||
图片预览

文档简介
人教版九年级数学上册第二十一章
《一元二次方程:公式法》学习任务单及作业设计
第一课时
【学习目标】
1.会用配方法解字母系数的一元二次方程.
2.了解石子对一元二次方程的根的决定作用.
3.注意求根公式的使用条件.
4.会用公式法解一元二次方程,熟悉解题的一般步骤.
5.了解学习公式法的原因.
【课前学习任务】
熟练掌握数字系数的一元二次方程的配方法,会用配方法解数字系数的一元二次方程.
【课上学习任务】
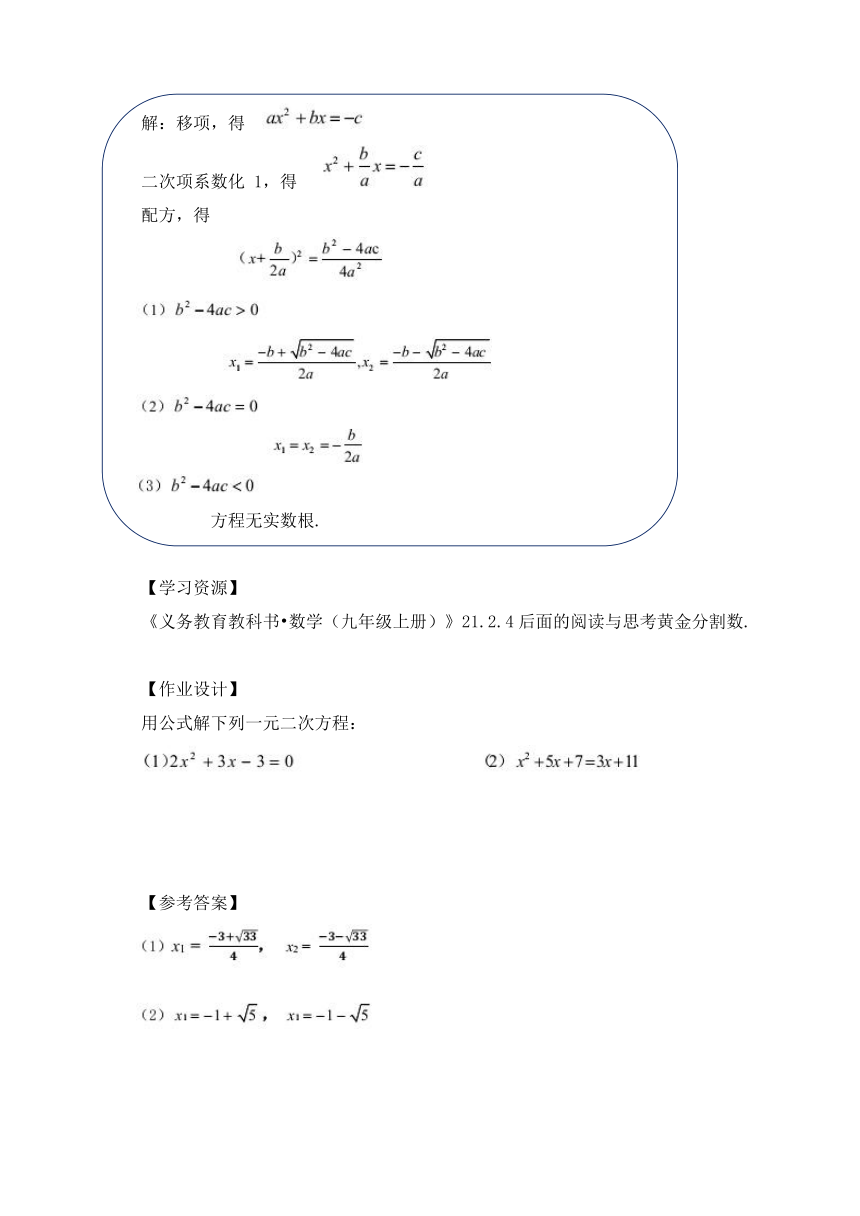
学习任务一:
用配方法解方程.
解:移项,得
合并同类项,得
二次项系数化 1,得
配方,得
学习任务二:
用配方法解关于 x 的一元二次方程.
解:移项,得
二次项系数化 1,得
配方,得
方程无实数根.
【学习资源】
《义务教育教科书 数学(九年级上册)》21.2.4后面的阅读与思考黄金分割数.
【作业设计】
用公式解下列一元二次方程:
【参考答案】
第二课时
【学习目标】
复习求根公式,会用公式法熟练的解一元二次方程; 会用公式法解简单的含字母系数的一元二次方程.
【课前学习任务】
复习之前学过的一元二次方程的解法.
【课上学习任务】
学习任务一:
(1)解方程.
(2)这道题小明和小华也给出了解答,请你看看他们的解答过程,思考:这两种解法有什么关系
小明用的是配方法, 写出了配方的过程, 小华直接应用了配方的结果, 用的是公式法, 操作更为简洁.
学习任务二:
例1:用公式法解下列方程:
分析:看第(1)小题方程的结构,等号左边是二次三项式,右边是0,它是一元二次方程的一般形式,首先明确a、b、c的值;其次把a、b、c的值代入,计算的值,并与 0 比较大小后, 我们得到原方程有两个相等实数根, 再代入求根公式得到方程的解.第(2)小题,显然不是一般形式,先将方程化为一般形式为,再按公式法解方程的步骤进行解答.第(3)小题在化为一般式后,计算的值为-4,-4 小于 0,所以原方程无实数根.答案:
学习任务三:
例2:用公式法解关于x的一元二次方程:
分析:(1)因为它是关于 x 的方程,所以方程中未知数是 x,m 看成常数,其次看方程的结构,它是一般式;再次明确 a、b、c 的值分别为,先将 a、b、 c 的值代入判别式△,计算出它的结果是,原方程有两个实数根.最后将 a、b、c 和判别式△的值代入公式求解.(2)首先可以观察到方程还是含有两个字母m和x,因为它是关于x的方程,所以未知数是x,m看成常数,其次看方程的结构,显然还是需要整理,化为的形式,即 . 这里 a、b、c 的值分别为a=m-2,b=-m,c=2,,所以原方程是一个关于x的一元二次方程,我们同第(1)小题一样用公式法来解答.
【作业设计】
请同学们在作业本上完成下面4道课后作业:
用公式法解下列关于x方程:
【参考答案】
《一元二次方程:公式法》学习任务单及作业设计
第一课时
【学习目标】
1.会用配方法解字母系数的一元二次方程.
2.了解石子对一元二次方程的根的决定作用.
3.注意求根公式的使用条件.
4.会用公式法解一元二次方程,熟悉解题的一般步骤.
5.了解学习公式法的原因.
【课前学习任务】
熟练掌握数字系数的一元二次方程的配方法,会用配方法解数字系数的一元二次方程.
【课上学习任务】
学习任务一:
用配方法解方程.
解:移项,得
合并同类项,得
二次项系数化 1,得
配方,得
学习任务二:
用配方法解关于 x 的一元二次方程.
解:移项,得
二次项系数化 1,得
配方,得
方程无实数根.
【学习资源】
《义务教育教科书 数学(九年级上册)》21.2.4后面的阅读与思考黄金分割数.
【作业设计】
用公式解下列一元二次方程:
【参考答案】
第二课时
【学习目标】
复习求根公式,会用公式法熟练的解一元二次方程; 会用公式法解简单的含字母系数的一元二次方程.
【课前学习任务】
复习之前学过的一元二次方程的解法.
【课上学习任务】
学习任务一:
(1)解方程.
(2)这道题小明和小华也给出了解答,请你看看他们的解答过程,思考:这两种解法有什么关系
小明用的是配方法, 写出了配方的过程, 小华直接应用了配方的结果, 用的是公式法, 操作更为简洁.
学习任务二:
例1:用公式法解下列方程:
分析:看第(1)小题方程的结构,等号左边是二次三项式,右边是0,它是一元二次方程的一般形式,首先明确a、b、c的值;其次把a、b、c的值代入,计算的值,并与 0 比较大小后, 我们得到原方程有两个相等实数根, 再代入求根公式得到方程的解.第(2)小题,显然不是一般形式,先将方程化为一般形式为,再按公式法解方程的步骤进行解答.第(3)小题在化为一般式后,计算的值为-4,-4 小于 0,所以原方程无实数根.答案:
学习任务三:
例2:用公式法解关于x的一元二次方程:
分析:(1)因为它是关于 x 的方程,所以方程中未知数是 x,m 看成常数,其次看方程的结构,它是一般式;再次明确 a、b、c 的值分别为,先将 a、b、 c 的值代入判别式△,计算出它的结果是,原方程有两个实数根.最后将 a、b、c 和判别式△的值代入公式求解.(2)首先可以观察到方程还是含有两个字母m和x,因为它是关于x的方程,所以未知数是x,m看成常数,其次看方程的结构,显然还是需要整理,化为的形式,即 . 这里 a、b、c 的值分别为a=m-2,b=-m,c=2,,所以原方程是一个关于x的一元二次方程,我们同第(1)小题一样用公式法来解答.
【作业设计】
请同学们在作业本上完成下面4道课后作业:
用公式法解下列关于x方程:
【参考答案】
同课章节目录
