【核心素养目标】数学人教版八年级上册11.1.1 三角形的边 教案 (表格式)
文档属性
| 名称 | 【核心素养目标】数学人教版八年级上册11.1.1 三角形的边 教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 691.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 20:58:05 | ||
图片预览


文档简介
11.1三角形
11.1.1三角形的边
教学内容 11.1.1三角形的边 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:通过展示生活中实际案例让学生从中观察抽象出三角形的概念,认识三角形的边、内角、顶点,能用符号语言表示三角形. 能识别不同形状的三角形. 2.会用数学的思维思考现实世界:在对三角形研究中,通过对趣味题目的思考,学习三角形边长的性质,让学生对三角形边长的性质进行猜想、推理和验证,并能运用三角形边长的性质解决实际生活中的数学问题. 3.会用数学的语言表示现实世界:在对三角形概念研究中,通过对三角形的分类和对三角形性质的探索,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1. 认识三角形的边、内角、顶点,能用几何语言表示三角形; 2. 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明; 3. 了解三角形分类的原则和结论.
教学重点 1.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明; 2.了解三角形分类的原则和结论.
教学难点 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明
教学准备 课件、直尺、A4纸。
教学过程 主要师生活动 设计意图
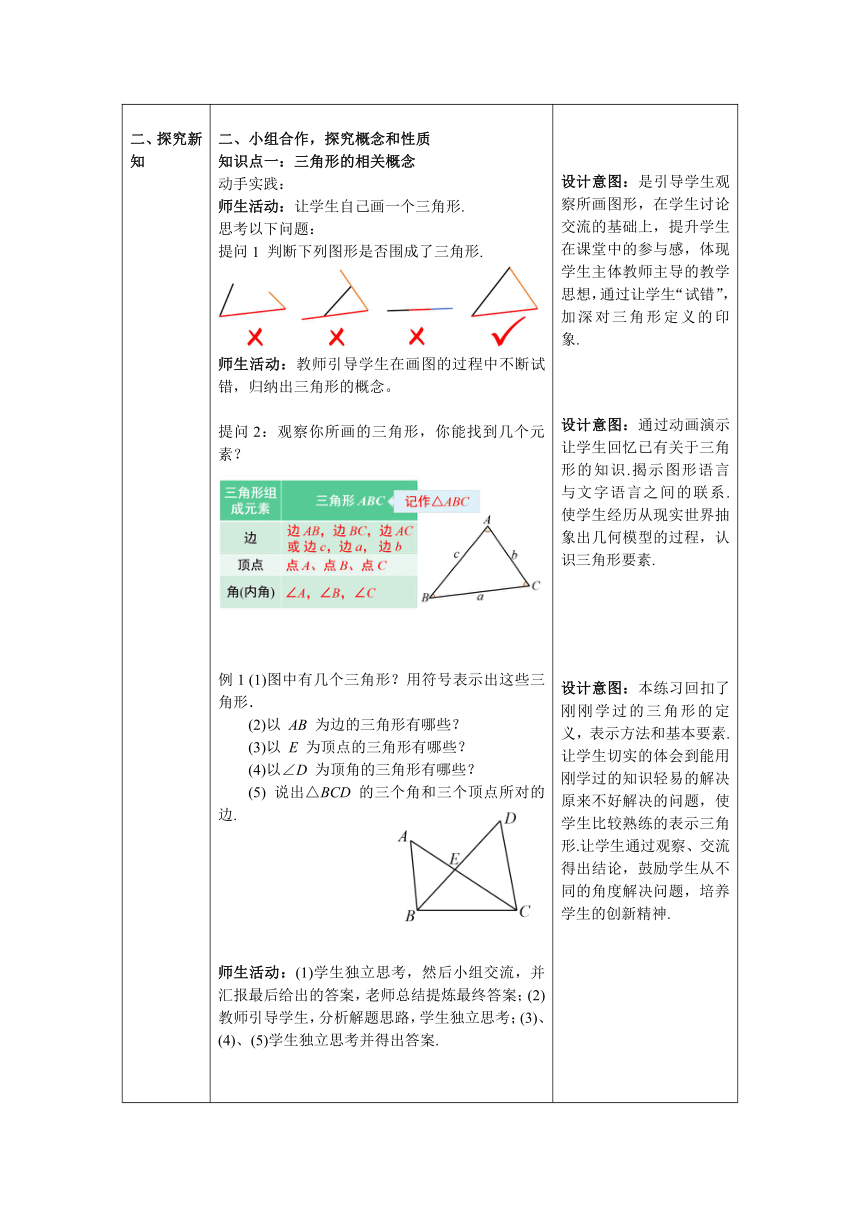
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 你能从下列图形中找出一些三角形吗? (借助多媒体把古埃及的金字塔、钢斜拉桥、塔吊、自行车的投影,给同学放映) 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点一:三角形的相关概念 动手实践: 师生活动:让学生自己画一个三角形. 思考以下问题: 提问1 判断下列图形是否围成了三角形. 师生活动:教师引导学生在画图的过程中不断试错,归纳出三角形的概念。 提问2:观察你所画的三角形,你能找到几个元素? 例1 (1)图中有几个三角形?用符号表示出这些三角形. (2)以 AB 为边的三角形有哪些? (3)以 E 为顶点的三角形有哪些? (4)以∠D 为顶角的三角形有哪些? (5) 说出△BCD 的三个角和三个顶点所对的边. 师生活动:(1)学生独立思考,然后小组交流,并汇报最后给出的答案,老师总结提炼最终答案;(2)教师引导学生,分析解题思路,学生独立思考;(3)、(4)、(5)学生独立思考并得出答案. 知识点二:三角形的分类 问题3:根据三角形的组成元素,尝试对以下三角形进行分类,并说说你的分类标准: 师生活动:先学生独自思考,再引导学生从角度的大小来考虑,然后小组讨论回答问题,师生共同总结: 师追问:还有其他分类标准吗?量一量! 师生活动:先学生独自思考,小组讨论回答问题,师生共同总结: 独立思考: 问题1 三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢? 问题2 三条线段应具备什么条件才能构成三角形呢? 合作探究: 探究 在一个三角形小路上,在 A 点的小狗,为了吃到 B 点的骨头,它有几条路线可以选择?哪条路线最快呢? 师生活动:学生独立思考并回答问题.有两条路线可以选择.教师引导学生,分析解题思路,写出解题模板,交给学生解决其余问题. 例2 下列长度的三条线段能否拼成三角形?为什么? (1) 6 cm、9 cm、3 cm;(2) 4 cm、5 cm、3 cm. 师生活动:教师引导学生,分析解题思路,请一名同学板书,其他学生独立思考解题. 总结:判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可. 例3 用一条长为 18 cm 的细绳围成一个等腰三角形. (1) 如果腰长是底边长的 2 倍,那么各边的长是多少? (2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么? 师生活动:教师引导学生,分析解题思路,学生独立思考解决问题. 三、当堂练习,巩固所学 1.如图,在△ACE 中,∠CEA 的对边是 AC . 2.已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为16 cm . 3.若三角形的两边长分别是 3 和 8,第三边长为奇数,求第三边的长. 设计意图:这样设计的目的是通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,体会到三角形是最简单,最基本的几何图形,在生活中随处可见.激发学生学习三角形的兴趣和热情,同时引出课题. 设计意图:是引导学生观察所画图形,在学生讨论交流的基础上,提升学生在课堂中的参与感,体现学生主体教师主导的教学思想,通过让学生“试错”,加深对三角形定义的印象. 设计意图:通过动画演示让学生回忆已有关于三角形的知识.揭示图形语言与文字语言之间的联系.使学生经历从现实世界抽象出几何模型的过程,认识三角形要素. 设计意图:本练习回扣了刚刚学过的三角形的定义,表示方法和基本要素.让学生切实的体会到能用刚学过的知识轻易的解决原来不好解决的问题,使学生比较熟练的表示三角形.让学生通过观察、交流得出结论,鼓励学生从不同的角度解决问题,培养学生的创新精神. 设计意图:以问题的形式引导学生对三角形按角、边进行分类。通过独立思考和合作探究来构建三角形分类的框架结构。形成对三角形不同类别特征的理性思考和初步感知. 设计意图:设计情景问题,让学生自发观察和讨论,利用两点之间线段最短,解决简单问题,对于学生的回答,只要合理都要予以肯定和鼓励.问题设置由浅入深,增强学生的自信,从解题中获得的满足感,激发对学生学习内驱力. 设计意图:一方面巩固刚刚学习的三角形三边的关系——两边之和大于第三边、两边之差小于第三边,另一方面帮助学生总结更简便的解题方法. 设计意图:巩固刚刚学习的三角形三边的关系的同时,让学生运用所学知识,学会规范答题,感悟几何计算严谨,明白学习本节知识点的意义. 设计意图: 考查学生对三角形的有关概念(边、角、顶点)的掌握. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想.
板书设计 三角形 三角形: 由不在同一条直线上的三条线段首尾顺次相接所组成的图形. 两条较短线段长之和是否大于第三条线段长.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能 为什么不能 初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
11.1.1三角形的边
教学内容 11.1.1三角形的边 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:通过展示生活中实际案例让学生从中观察抽象出三角形的概念,认识三角形的边、内角、顶点,能用符号语言表示三角形. 能识别不同形状的三角形. 2.会用数学的思维思考现实世界:在对三角形研究中,通过对趣味题目的思考,学习三角形边长的性质,让学生对三角形边长的性质进行猜想、推理和验证,并能运用三角形边长的性质解决实际生活中的数学问题. 3.会用数学的语言表示现实世界:在对三角形概念研究中,通过对三角形的分类和对三角形性质的探索,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1. 认识三角形的边、内角、顶点,能用几何语言表示三角形; 2. 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明; 3. 了解三角形分类的原则和结论.
教学重点 1.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明; 2.了解三角形分类的原则和结论.
教学难点 掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明
教学准备 课件、直尺、A4纸。
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 你能从下列图形中找出一些三角形吗? (借助多媒体把古埃及的金字塔、钢斜拉桥、塔吊、自行车的投影,给同学放映) 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点一:三角形的相关概念 动手实践: 师生活动:让学生自己画一个三角形. 思考以下问题: 提问1 判断下列图形是否围成了三角形. 师生活动:教师引导学生在画图的过程中不断试错,归纳出三角形的概念。 提问2:观察你所画的三角形,你能找到几个元素? 例1 (1)图中有几个三角形?用符号表示出这些三角形. (2)以 AB 为边的三角形有哪些? (3)以 E 为顶点的三角形有哪些? (4)以∠D 为顶角的三角形有哪些? (5) 说出△BCD 的三个角和三个顶点所对的边. 师生活动:(1)学生独立思考,然后小组交流,并汇报最后给出的答案,老师总结提炼最终答案;(2)教师引导学生,分析解题思路,学生独立思考;(3)、(4)、(5)学生独立思考并得出答案. 知识点二:三角形的分类 问题3:根据三角形的组成元素,尝试对以下三角形进行分类,并说说你的分类标准: 师生活动:先学生独自思考,再引导学生从角度的大小来考虑,然后小组讨论回答问题,师生共同总结: 师追问:还有其他分类标准吗?量一量! 师生活动:先学生独自思考,小组讨论回答问题,师生共同总结: 独立思考: 问题1 三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢? 问题2 三条线段应具备什么条件才能构成三角形呢? 合作探究: 探究 在一个三角形小路上,在 A 点的小狗,为了吃到 B 点的骨头,它有几条路线可以选择?哪条路线最快呢? 师生活动:学生独立思考并回答问题.有两条路线可以选择.教师引导学生,分析解题思路,写出解题模板,交给学生解决其余问题. 例2 下列长度的三条线段能否拼成三角形?为什么? (1) 6 cm、9 cm、3 cm;(2) 4 cm、5 cm、3 cm. 师生活动:教师引导学生,分析解题思路,请一名同学板书,其他学生独立思考解题. 总结:判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可. 例3 用一条长为 18 cm 的细绳围成一个等腰三角形. (1) 如果腰长是底边长的 2 倍,那么各边的长是多少? (2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么? 师生活动:教师引导学生,分析解题思路,学生独立思考解决问题. 三、当堂练习,巩固所学 1.如图,在△ACE 中,∠CEA 的对边是 AC . 2.已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为16 cm . 3.若三角形的两边长分别是 3 和 8,第三边长为奇数,求第三边的长. 设计意图:这样设计的目的是通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,体会到三角形是最简单,最基本的几何图形,在生活中随处可见.激发学生学习三角形的兴趣和热情,同时引出课题. 设计意图:是引导学生观察所画图形,在学生讨论交流的基础上,提升学生在课堂中的参与感,体现学生主体教师主导的教学思想,通过让学生“试错”,加深对三角形定义的印象. 设计意图:通过动画演示让学生回忆已有关于三角形的知识.揭示图形语言与文字语言之间的联系.使学生经历从现实世界抽象出几何模型的过程,认识三角形要素. 设计意图:本练习回扣了刚刚学过的三角形的定义,表示方法和基本要素.让学生切实的体会到能用刚学过的知识轻易的解决原来不好解决的问题,使学生比较熟练的表示三角形.让学生通过观察、交流得出结论,鼓励学生从不同的角度解决问题,培养学生的创新精神. 设计意图:以问题的形式引导学生对三角形按角、边进行分类。通过独立思考和合作探究来构建三角形分类的框架结构。形成对三角形不同类别特征的理性思考和初步感知. 设计意图:设计情景问题,让学生自发观察和讨论,利用两点之间线段最短,解决简单问题,对于学生的回答,只要合理都要予以肯定和鼓励.问题设置由浅入深,增强学生的自信,从解题中获得的满足感,激发对学生学习内驱力. 设计意图:一方面巩固刚刚学习的三角形三边的关系——两边之和大于第三边、两边之差小于第三边,另一方面帮助学生总结更简便的解题方法. 设计意图:巩固刚刚学习的三角形三边的关系的同时,让学生运用所学知识,学会规范答题,感悟几何计算严谨,明白学习本节知识点的意义. 设计意图: 考查学生对三角形的有关概念(边、角、顶点)的掌握. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想.
板书设计 三角形 三角形: 由不在同一条直线上的三条线段首尾顺次相接所组成的图形. 两条较短线段长之和是否大于第三条线段长.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能 为什么不能 初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
