【核心素养目标】数学人教版八年级上册12.1 全等三角形 教案 (表格式)
文档属性
| 名称 | 【核心素养目标】数学人教版八年级上册12.1 全等三角形 教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 987.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览

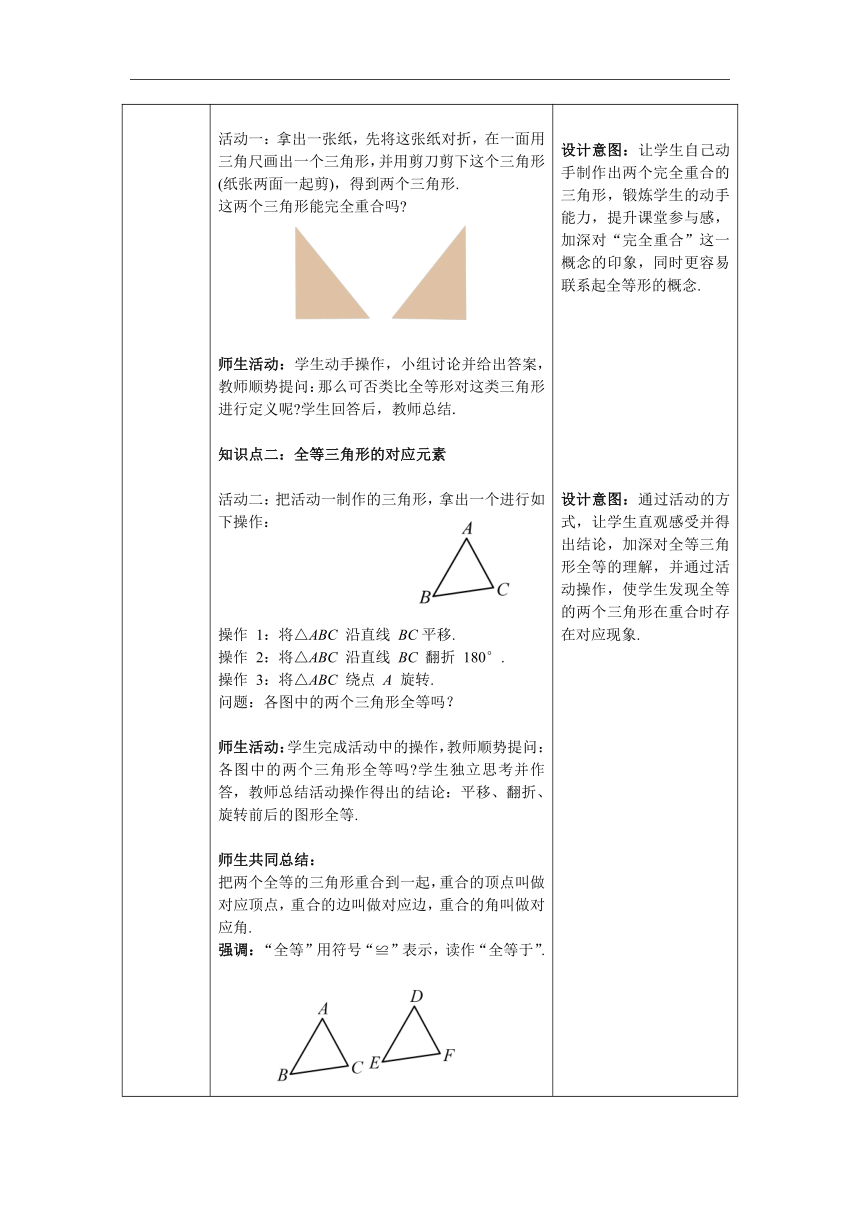
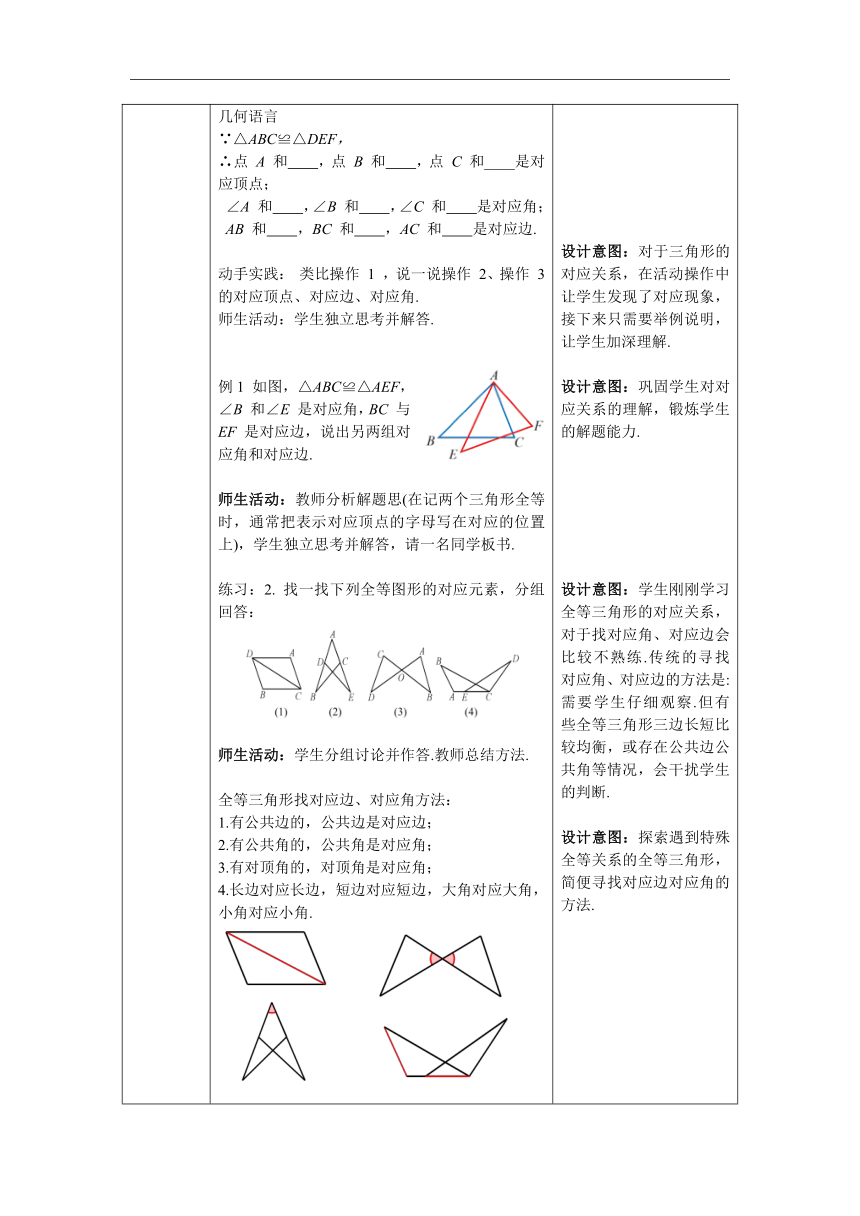
文档简介
12.1 全等三角形
教学内容 12.1 全等三角形 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,学生通过观察,初步理解全等的概念,总结全等形在实际生活中的含义. 2.会用数学的思维思考现实世界:在对全等形和全等三角形的研究中,探究全等形和全等三角形的关系,培养类比推理的数学思维. 3.会用数学的语言表示现实世界:通过对全等三角形概念和性质的学习,在经历猜想、验证、归纳的学习过程中,体会归纳的数学思想方法,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1.理解全等形和全等三角形的概念,能识别全等三角形中的对应顶点、对应边、对应角. 2掌握全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
教学重点 探究全等三角形的性质的过程.
教学难点 正确找出全等三角形中的对应边和对应角.
教学准备 课件,纸,量角器,三角板等
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 教师叙述:观察下面各组图形,说说它们有什么共同特点. 师生活动:学生独立思考并作答,教师总结(都是由形状、大小相同的图形构成的). 二、小组合作,探究概念和性质 知识点一:全等三角形的定义 思考1 翻动课本,把每页纸看作一个图形,那么这些图形有什么样的特点呢 活动一:拿出一张纸,先将这张纸对折,在一面用三角尺画出一个三角形,并用剪刀剪下这个三角形(纸张两面一起剪),得到两个三角形. 这两个三角形能完全重合吗 师生活动:学生动手操作,小组讨论并给出答案,教师顺势提问:那么可否类比全等形对这类三角形进行定义呢 学生回答后,教师总结. 知识点二:全等三角形的对应元素 活动二:把活动一制作的三角形,拿出一个进行如下操作: 操作 1:将△ABC 沿直线 BC平移. 操作 2:将△ABC 沿直线 BC 翻折 180°. 操作 3:将△ABC 绕点 A 旋转. 问题:各图中的两个三角形全等吗? 师生活动:学生完成活动中的操作,教师顺势提问:各图中的两个三角形全等吗 学生独立思考并作答,教师总结活动操作得出的结论:平移、翻折、旋转前后的图形全等. 师生共同总结: 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角. 强调:“全等”用符号“≌”表示,读作“全等于”. 几何语言 ∵△ABC≌△DEF, ∴点 A 和 ,点 B 和 ,点 C 和____是对应顶点; ∠A 和 ,∠B 和 ,∠C 和 是对应角; AB 和 ,BC 和 ,AC 和 是对应边. 动手实践: 类比操作 1 ,说一说操作 2、操作 3 的对应顶点、对应边、对应角. 师生活动:学生独立思考并解答. 例1 如图,△ABC≌△AEF, ∠B 和∠E 是对应角,BC 与 EF 是对应边,说出另两组对应角和对应边. 师生活动:教师分析解题思(在记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上),学生独立思考并解答,请一名同学板书. 练习:2. 找一找下列全等图形的对应元素,分组回答: 师生活动:学生分组讨论并作答.教师总结方法. 全等三角形找对应边、对应角方法: 1.有公共边的,公共边是对应边; 2.有公共角的,公共角是对应角; 3.有对顶角的,对顶角是对应角; 4.长边对应长边,短边对应短边,大角对应大角,小角对应小角. 思考2在操作 1 中,将△ABC 沿直线 BC 平移得到△DEF,对应边有什么关系,对应角呢 师生活动:教师引导学生,分析思路(猜一猜→想一想),请同学们思考对应边和对应角可能存在的数量关系. 猜一猜:全等三角形的对应边相等,全等三角形的对应角相等. 量一量:请学生用量角器和刻度尺测量制作的两个三角形的角度及边长. 师生共同归纳: 全等三角形的性质: 全等三角形的对应边______,全等三角形的对应角______. 几何语言: ∵△ABC≌△FDE, ∴A B = F D,A C = F E,B C = D E,(对应边相等) ∠A =∠F,∠B =∠D,∠C =∠E.(对应角相等) 例2 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠E 的度数和 CF 的长. 师生活动:学生独立思考解题,教师板书并理清解题思路. 三、当堂练习,巩固所学 1.下列说法中,不正确的是 ( ) A. 两个全等形的对应边相等,对应角相等 B. 两个全等三角形的周长一定相等 C. 两个全等形一定关于某条直线翻折后重合 D. 两个全等三角形的面积一定相等 2. (德城区校级期末)如图,点 E 在 AC,△ABC≌△DAE,BC = 3,DE = 7,则 C的长为 ( ) A. 2 B. 3 C. 4 D. 5 (南昌期末)如图,将△ABC 绕点 A 顺时针旋转,得到△ADE,点 E 落在 BC 上,猜想∠BAD 和∠BED 之间的数量关系,并说明理由. 设计意图:这样设计的目的是通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,学生通过观察,初步理解全等的概念. 设计意图:由身边最常见的事物入手,学生翻动书本,很容易联想到书面每一页都会重合起来,从而引出全等的概念和性质. 设计意图:让学生自己动手制作出两个完全重合的三角形,锻炼学生的动手能力,提升课堂参与感,加深对“完全重合”这一概念的印象,同时更容易联系起全等形的概念. 设计意图:通过活动的方式,让学生直观感受并得出结论,加深对全等三角形全等的理解,并通过活动操作,使学生发现全等的两个三角形在重合时存在对应现象. 设计意图:对于三角形的对应关系,在活动操作中让学生发现了对应现象,接下来只需要举例说明,让学生加深理解. 设计意图:巩固学生对对应关系的理解,锻炼学生的解题能力. 设计意图:学生刚刚学习全等三角形的对应关系,对于找对应角、对应边会比较不熟练.传统的寻找对应角、对应边的方法是:需要学生仔细观察.但有些全等三角形三边长短比较均衡,或存在公共边公共角等情况,会干扰学生的判断. 设计意图:探索遇到特殊全等关系的全等三角形,简便寻找对应边对应角的方法. 设计意图:学生学习了对应边和对应角,这时猜测对应边、对应角之间的关系并不难,这里只让学生进行简单测量,认识客观性质. 设计意图:巩固刚学习的全等三角形的性质,教师板书规范学生学习正确的几何语言解题方式. 设计意图: 考查学生对全等三角形性质的掌握. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想.
板书设计 全等三角形 全等三角形: ∵△ABC≌△FDE, ∴A B = F D,A C = F E,B C = D E,(对应边相等) ∠A =∠F,∠B =∠D,∠C =∠E.(对应角相等)
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课是在学习了线段、角、相交线与平行线以及三角形的有关知识的根底上,学习全等三角形的概念和性质,全等三角形的对应边和对应角是后面判定三角形全等、应用三角形全等证明线段相等或角相等时常用到的概念,所以,要根据具体情况,针对两个全等三角形不同的位置关系,准确地找出它们的对应边和对应角. 对应边、对应角、对边、对角容易混淆.对应边、对应角是两个三角形的两条边之间或两个角之间的关系.而对边、对角是同一个三角形中边和角之间的关系,教学时要结合图形说清楚.学生观察、发现生活中的全等形,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.在图形变换以及实际操作的过程中,获得全等三角形的体验,在探索全等三角形性质的过程中,开展学生的空间观念,培养学生的几何直觉,感受到数学的乐趣.
教学内容 12.1 全等三角形 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,学生通过观察,初步理解全等的概念,总结全等形在实际生活中的含义. 2.会用数学的思维思考现实世界:在对全等形和全等三角形的研究中,探究全等形和全等三角形的关系,培养类比推理的数学思维. 3.会用数学的语言表示现实世界:通过对全等三角形概念和性质的学习,在经历猜想、验证、归纳的学习过程中,体会归纳的数学思想方法,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1.理解全等形和全等三角形的概念,能识别全等三角形中的对应顶点、对应边、对应角. 2掌握全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.
教学重点 探究全等三角形的性质的过程.
教学难点 正确找出全等三角形中的对应边和对应角.
教学准备 课件,纸,量角器,三角板等
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 教师叙述:观察下面各组图形,说说它们有什么共同特点. 师生活动:学生独立思考并作答,教师总结(都是由形状、大小相同的图形构成的). 二、小组合作,探究概念和性质 知识点一:全等三角形的定义 思考1 翻动课本,把每页纸看作一个图形,那么这些图形有什么样的特点呢 活动一:拿出一张纸,先将这张纸对折,在一面用三角尺画出一个三角形,并用剪刀剪下这个三角形(纸张两面一起剪),得到两个三角形. 这两个三角形能完全重合吗 师生活动:学生动手操作,小组讨论并给出答案,教师顺势提问:那么可否类比全等形对这类三角形进行定义呢 学生回答后,教师总结. 知识点二:全等三角形的对应元素 活动二:把活动一制作的三角形,拿出一个进行如下操作: 操作 1:将△ABC 沿直线 BC平移. 操作 2:将△ABC 沿直线 BC 翻折 180°. 操作 3:将△ABC 绕点 A 旋转. 问题:各图中的两个三角形全等吗? 师生活动:学生完成活动中的操作,教师顺势提问:各图中的两个三角形全等吗 学生独立思考并作答,教师总结活动操作得出的结论:平移、翻折、旋转前后的图形全等. 师生共同总结: 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角. 强调:“全等”用符号“≌”表示,读作“全等于”. 几何语言 ∵△ABC≌△DEF, ∴点 A 和 ,点 B 和 ,点 C 和____是对应顶点; ∠A 和 ,∠B 和 ,∠C 和 是对应角; AB 和 ,BC 和 ,AC 和 是对应边. 动手实践: 类比操作 1 ,说一说操作 2、操作 3 的对应顶点、对应边、对应角. 师生活动:学生独立思考并解答. 例1 如图,△ABC≌△AEF, ∠B 和∠E 是对应角,BC 与 EF 是对应边,说出另两组对应角和对应边. 师生活动:教师分析解题思(在记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上),学生独立思考并解答,请一名同学板书. 练习:2. 找一找下列全等图形的对应元素,分组回答: 师生活动:学生分组讨论并作答.教师总结方法. 全等三角形找对应边、对应角方法: 1.有公共边的,公共边是对应边; 2.有公共角的,公共角是对应角; 3.有对顶角的,对顶角是对应角; 4.长边对应长边,短边对应短边,大角对应大角,小角对应小角. 思考2在操作 1 中,将△ABC 沿直线 BC 平移得到△DEF,对应边有什么关系,对应角呢 师生活动:教师引导学生,分析思路(猜一猜→想一想),请同学们思考对应边和对应角可能存在的数量关系. 猜一猜:全等三角形的对应边相等,全等三角形的对应角相等. 量一量:请学生用量角器和刻度尺测量制作的两个三角形的角度及边长. 师生共同归纳: 全等三角形的性质: 全等三角形的对应边______,全等三角形的对应角______. 几何语言: ∵△ABC≌△FDE, ∴A B = F D,A C = F E,B C = D E,(对应边相等) ∠A =∠F,∠B =∠D,∠C =∠E.(对应角相等) 例2 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠E 的度数和 CF 的长. 师生活动:学生独立思考解题,教师板书并理清解题思路. 三、当堂练习,巩固所学 1.下列说法中,不正确的是 ( ) A. 两个全等形的对应边相等,对应角相等 B. 两个全等三角形的周长一定相等 C. 两个全等形一定关于某条直线翻折后重合 D. 两个全等三角形的面积一定相等 2. (德城区校级期末)如图,点 E 在 AC,△ABC≌△DAE,BC = 3,DE = 7,则 C的长为 ( ) A. 2 B. 3 C. 4 D. 5 (南昌期末)如图,将△ABC 绕点 A 顺时针旋转,得到△ADE,点 E 落在 BC 上,猜想∠BAD 和∠BED 之间的数量关系,并说明理由. 设计意图:这样设计的目的是通过展示学生熟知的实际生活图片,让学生经历几何模型的抽象过程,学生通过观察,初步理解全等的概念. 设计意图:由身边最常见的事物入手,学生翻动书本,很容易联想到书面每一页都会重合起来,从而引出全等的概念和性质. 设计意图:让学生自己动手制作出两个完全重合的三角形,锻炼学生的动手能力,提升课堂参与感,加深对“完全重合”这一概念的印象,同时更容易联系起全等形的概念. 设计意图:通过活动的方式,让学生直观感受并得出结论,加深对全等三角形全等的理解,并通过活动操作,使学生发现全等的两个三角形在重合时存在对应现象. 设计意图:对于三角形的对应关系,在活动操作中让学生发现了对应现象,接下来只需要举例说明,让学生加深理解. 设计意图:巩固学生对对应关系的理解,锻炼学生的解题能力. 设计意图:学生刚刚学习全等三角形的对应关系,对于找对应角、对应边会比较不熟练.传统的寻找对应角、对应边的方法是:需要学生仔细观察.但有些全等三角形三边长短比较均衡,或存在公共边公共角等情况,会干扰学生的判断. 设计意图:探索遇到特殊全等关系的全等三角形,简便寻找对应边对应角的方法. 设计意图:学生学习了对应边和对应角,这时猜测对应边、对应角之间的关系并不难,这里只让学生进行简单测量,认识客观性质. 设计意图:巩固刚学习的全等三角形的性质,教师板书规范学生学习正确的几何语言解题方式. 设计意图: 考查学生对全等三角形性质的掌握. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想. 设计意图: 考查学生分类讨论和运用三角形三边不等的关系解决问题的思想.
板书设计 全等三角形 全等三角形: ∵△ABC≌△FDE, ∴A B = F D,A C = F E,B C = D E,(对应边相等) ∠A =∠F,∠B =∠D,∠C =∠E.(对应角相等)
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课是在学习了线段、角、相交线与平行线以及三角形的有关知识的根底上,学习全等三角形的概念和性质,全等三角形的对应边和对应角是后面判定三角形全等、应用三角形全等证明线段相等或角相等时常用到的概念,所以,要根据具体情况,针对两个全等三角形不同的位置关系,准确地找出它们的对应边和对应角. 对应边、对应角、对边、对角容易混淆.对应边、对应角是两个三角形的两条边之间或两个角之间的关系.而对边、对角是同一个三角形中边和角之间的关系,教学时要结合图形说清楚.学生观察、发现生活中的全等形,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.在图形变换以及实际操作的过程中,获得全等三角形的体验,在探索全等三角形性质的过程中,开展学生的空间观念,培养学生的几何直觉,感受到数学的乐趣.
