【核心素养目标】数学人教版八年级上册13.3.1 第1课时 等腰三角形的性质 教案 (表格式)
文档属性
| 名称 | 【核心素养目标】数学人教版八年级上册13.3.1 第1课时 等腰三角形的性质 教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 596.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览


文档简介
13.3.1 等腰三角形
第1课时 等腰三角形的性质
教学内容 第1课时 等腰三角形的性质 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:用实际生活中的景物导入,吸引学生的注意力的同时,感悟等腰三角形在实际生活中的应用,激发学生的兴趣,让学生感受到生活中处处有数学. 2.会用数学的思维思考现实世界:用生活情境导入,提高学生的分析问题和用数学语言总结生活问题的能力,让学生体会数学的应用价值,培养类比、分类讨论的数学思维. 3.会用数学的语言表示现实世界:通过对用等腰三角形的性质的学习,在经历猜想、验证、归纳的学习过程中,体会归纳的数学思想方法,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1.探索并证明等腰三角形的两个性质. 2.能利用等腰三角形的性质证明两个角相等或两条线段相等. 3.结合等腰三角形性质的探索与证明过程,体会轴对称在研究几何问题中的作用.
教学重点 探索并证明等腰三角形性质.
教学难点 性质1证明中辅助线的添加和对性质2的理解.
教学准备 课件
教学过程 主要师生活动 设计意图
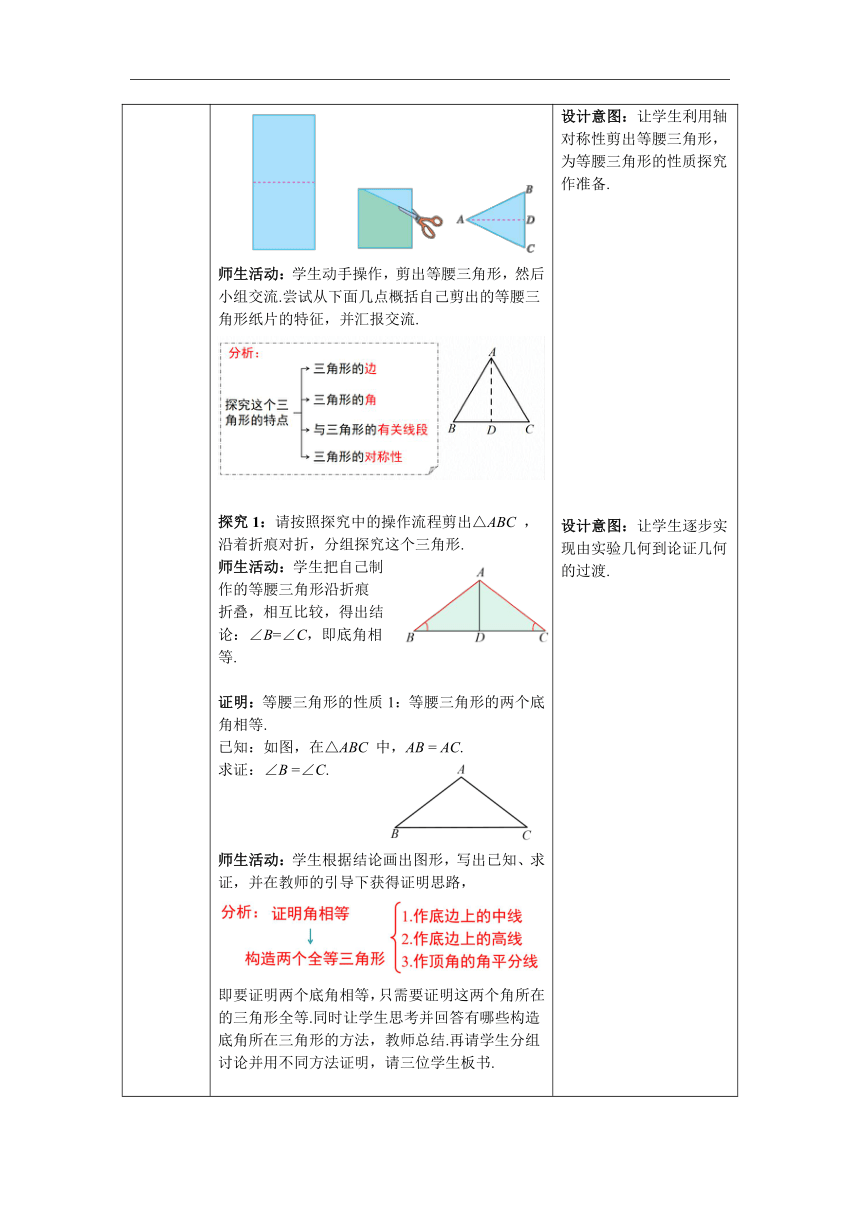
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 新课导入:在故宫博物馆中,有很多建筑设计成等腰三角形,例如下图的中和殿的屋檐设计,你能说说为什么吗? 二、小组合作,探究概念和性质 知识点:等腰三角形的性质 活动:如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC 有什么特点? 师生活动:学生动手操作,剪出等腰三角形,然后小组交流.尝试从下面几点概括自己剪出的等腰三角形纸片的特征,并汇报交流. 探究1:请按照探究中的操作流程剪出△ABC ,沿着折痕对折,分组探究这个三角形. 师生活动:学生把自己制作的等腰三角形沿折痕折叠,相互比较,得出结论:∠B=∠C,即底角相等. 证明:等腰三角形的性质1:等腰三角形的两个底角相等. 已知:如图,在△ABC 中,AB = AC. 求证:∠B =∠C. 师生活动:学生根据结论画出图形,写出已知、求证,并在教师的引导下获得证明思路, 即要证明两个底角相等,只需要证明这两个角所在的三角形全等.同时让学生思考并回答有哪些构造底角所在三角形的方法,教师总结.再请学生分组讨论并用不同方法证明,请三位学生板书. 师生共同得出: 等腰三角形的性质1: 等腰三角形的两个底角______(简写成“等边对等角”). 几何语言: ∵ △ABC 是等腰三角形, ∴ ____=____(等角对等边). 探究2:在上述不同方法的证明过程中,由三角形顶角作的底边上的中线、高线、顶角角平分线有什么特点? 师生活动:让学生观察并得出猜想——完全重合. 证明:等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合. 已知:如图,在△ABC 中,AB = AC,BD = DC,求证 AD⊥BC,DA 平分∠BAC. 师生活动:学生在教师的引导下,分析证明思路——证明三线合一,可以假设任意一种线段为已知条件,再证明该线段符合其他线段的定义.学生独立思考完成证明, 师追问:这三条线是否在任意边上都重合? 师生活动:让学生独立思考,回答问题. 教师总结:等腰三角形的性质2. 追问:你能翻译成几何语言吗? 师生活动:教师留实践给学生思考随后播放PPT,让学生完成如下填空: (1)∵△ABC是等腰三角形, BD = CD (已知) ∴______________,________ (等腰三角形的“三线合一”) (2)∵△ABC是等腰三角形,∠BAD=∠CAD (已知) ∴_________,AD⊥BC,_________________________ (3)∵△ABC 是等腰三角形,AD⊥BC ∴BD = CD,______________(等腰三角形的“三线合一”) 师生共同总结: 典例精析: 例1 如图,在△ABC 中,AB = AC,点 D 在 AC 上,且 BD = BC = AD, 求 △ABC 各角的度数. 师生活动:学生分析题中条件和解题思路,云何永方程知识和三角形内角和定理即可求出△ABC各角的度数.学生解答,师生共同交流. 例2 已知点 D、E 在△ABC 的边 BC 上,AB=AC. (1) 如图①,若 AD=AE,求证:BD=CE; (2) 如图②,若 BD=CE,F 为 DE 的中点,求证:AF⊥BC. 师生活动:学生分析题中条件和解题思路,独立完成解答. 三、当堂练习,巩固所学 1. 等腰三角形的一个角为 70° ,则这个等腰三角形的顶角是 ( ) A. 70° B. 40°
C. 55° 或 70° D. 70° 或 40° 2.如图,已知 OA=OB=OC,且∠ACB=25°,求 ∠AOB 的大小. 3. (1) 等腰三角形一个底角为 75°,它的另外两个角的度数为__________; (2) 等腰三角形的一个角为 36°,它的另外两个角的度数为____________________; (3) 等腰三角形的一个角为 120°,它的另外两个角的度数为__________. 如图,已知 AB=AC,D 是 BC 边上的中点,求 ∠B= 30°,求 ∠BAD 和 ∠ADC 的度数. 设计意图:用实际生活中的景物导入,吸引学生的注意力的同时,感悟数学知识在实际生活中的应用. 设计意图:让学生利用轴对称性剪出等腰三角形,为等腰三角形的性质探究作准备. 设计意图:让学生逐步实现由实验几何到论证几何的过渡. 设计意图:通过自主独立的猜想,让学生在反复比较的过程中发现等腰三角形共同的、本质的特征;体会认识事物的一般方法——由特殊到一般,进一步培养学生抽象概括能力;让学生真正理“三线合一”的含义,并在严谨的证明过程中,体会等腰三角形性质2的内容实质. 设计意图:回扣课前一起讨论的问题,用精简的语言总结出本节课所探讨的问题的结论,前后相互对应,让学生对本节课学习的思维逻辑更加的清晰. 设计意图:通过逻辑推理和方程思想求出等腰三角形中的角的度数,让学生进一步巩固等腰三角形的性质1. 设计意图:让学生进一步巩固等腰三角形的性质1的同时,加强对等腰三角形性质2的运用,培养学生添加辅助线的能力. 设计意图:考查学生对等腰三角形性质1的掌握,运用等腰三角形性质1进行简单计算的能力. 设计意图:考查学生对等腰三角形性质1的掌握,和分类讨论的能力. 设计意图:考查学生对等腰三角形性质2的掌握,综合运用性质1和性质2解解决数学问题的能力.
板书设计 等腰三角形的性质1:等腰三角形的两个底角 相等 (简写成“等边对等角”). 等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高 相互重合 (简写成“三线合一”,注意:腰上的高和中线与底角的平分线不具有这一性质.).
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课是在学生已经学习了三角形的基本概念、全等三角形和轴对称知识的基础上,进一步研究特殊的三角形——等腰三角形、等腰三角形的性质为证明两个角相等、两条线段相等、两条直线垂直提供了方法,也是后续学习等边三角形、菱形、正方形、圆等内容的重要基础. 等腰三角形性质的探索是通过轴对称进行的,借助于轴对称发现了等腰三角形的性质,也获得了添加辅助线证明性质的方法.性质的证明是将欲证明相等的两个角(或线段)置于两个全等三角形之中,这是证明两个角相等或两条线段相等的基本策略之一.等腰三角形性质的探索与证明体现了转化的思想.
第1课时 等腰三角形的性质
教学内容 第1课时 等腰三角形的性质 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:用实际生活中的景物导入,吸引学生的注意力的同时,感悟等腰三角形在实际生活中的应用,激发学生的兴趣,让学生感受到生活中处处有数学. 2.会用数学的思维思考现实世界:用生活情境导入,提高学生的分析问题和用数学语言总结生活问题的能力,让学生体会数学的应用价值,培养类比、分类讨论的数学思维. 3.会用数学的语言表示现实世界:通过对用等腰三角形的性质的学习,在经历猜想、验证、归纳的学习过程中,体会归纳的数学思想方法,逐步养成用数学语言表达与交流的习惯,感悟数据的意义与价值.
知识目标 1.探索并证明等腰三角形的两个性质. 2.能利用等腰三角形的性质证明两个角相等或两条线段相等. 3.结合等腰三角形性质的探索与证明过程,体会轴对称在研究几何问题中的作用.
教学重点 探索并证明等腰三角形性质.
教学难点 性质1证明中辅助线的添加和对性质2的理解.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 新课导入:在故宫博物馆中,有很多建筑设计成等腰三角形,例如下图的中和殿的屋檐设计,你能说说为什么吗? 二、小组合作,探究概念和性质 知识点:等腰三角形的性质 活动:如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC 有什么特点? 师生活动:学生动手操作,剪出等腰三角形,然后小组交流.尝试从下面几点概括自己剪出的等腰三角形纸片的特征,并汇报交流. 探究1:请按照探究中的操作流程剪出△ABC ,沿着折痕对折,分组探究这个三角形. 师生活动:学生把自己制作的等腰三角形沿折痕折叠,相互比较,得出结论:∠B=∠C,即底角相等. 证明:等腰三角形的性质1:等腰三角形的两个底角相等. 已知:如图,在△ABC 中,AB = AC. 求证:∠B =∠C. 师生活动:学生根据结论画出图形,写出已知、求证,并在教师的引导下获得证明思路, 即要证明两个底角相等,只需要证明这两个角所在的三角形全等.同时让学生思考并回答有哪些构造底角所在三角形的方法,教师总结.再请学生分组讨论并用不同方法证明,请三位学生板书. 师生共同得出: 等腰三角形的性质1: 等腰三角形的两个底角______(简写成“等边对等角”). 几何语言: ∵ △ABC 是等腰三角形, ∴ ____=____(等角对等边). 探究2:在上述不同方法的证明过程中,由三角形顶角作的底边上的中线、高线、顶角角平分线有什么特点? 师生活动:让学生观察并得出猜想——完全重合. 证明:等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合. 已知:如图,在△ABC 中,AB = AC,BD = DC,求证 AD⊥BC,DA 平分∠BAC. 师生活动:学生在教师的引导下,分析证明思路——证明三线合一,可以假设任意一种线段为已知条件,再证明该线段符合其他线段的定义.学生独立思考完成证明, 师追问:这三条线是否在任意边上都重合? 师生活动:让学生独立思考,回答问题. 教师总结:等腰三角形的性质2. 追问:你能翻译成几何语言吗? 师生活动:教师留实践给学生思考随后播放PPT,让学生完成如下填空: (1)∵△ABC是等腰三角形, BD = CD (已知) ∴______________,________ (等腰三角形的“三线合一”) (2)∵△ABC是等腰三角形,∠BAD=∠CAD (已知) ∴_________,AD⊥BC,_________________________ (3)∵△ABC 是等腰三角形,AD⊥BC ∴BD = CD,______________(等腰三角形的“三线合一”) 师生共同总结: 典例精析: 例1 如图,在△ABC 中,AB = AC,点 D 在 AC 上,且 BD = BC = AD, 求 △ABC 各角的度数. 师生活动:学生分析题中条件和解题思路,云何永方程知识和三角形内角和定理即可求出△ABC各角的度数.学生解答,师生共同交流. 例2 已知点 D、E 在△ABC 的边 BC 上,AB=AC. (1) 如图①,若 AD=AE,求证:BD=CE; (2) 如图②,若 BD=CE,F 为 DE 的中点,求证:AF⊥BC. 师生活动:学生分析题中条件和解题思路,独立完成解答. 三、当堂练习,巩固所学 1. 等腰三角形的一个角为 70° ,则这个等腰三角形的顶角是 ( ) A. 70° B. 40°
C. 55° 或 70° D. 70° 或 40° 2.如图,已知 OA=OB=OC,且∠ACB=25°,求 ∠AOB 的大小. 3. (1) 等腰三角形一个底角为 75°,它的另外两个角的度数为__________; (2) 等腰三角形的一个角为 36°,它的另外两个角的度数为____________________; (3) 等腰三角形的一个角为 120°,它的另外两个角的度数为__________. 如图,已知 AB=AC,D 是 BC 边上的中点,求 ∠B= 30°,求 ∠BAD 和 ∠ADC 的度数. 设计意图:用实际生活中的景物导入,吸引学生的注意力的同时,感悟数学知识在实际生活中的应用. 设计意图:让学生利用轴对称性剪出等腰三角形,为等腰三角形的性质探究作准备. 设计意图:让学生逐步实现由实验几何到论证几何的过渡. 设计意图:通过自主独立的猜想,让学生在反复比较的过程中发现等腰三角形共同的、本质的特征;体会认识事物的一般方法——由特殊到一般,进一步培养学生抽象概括能力;让学生真正理“三线合一”的含义,并在严谨的证明过程中,体会等腰三角形性质2的内容实质. 设计意图:回扣课前一起讨论的问题,用精简的语言总结出本节课所探讨的问题的结论,前后相互对应,让学生对本节课学习的思维逻辑更加的清晰. 设计意图:通过逻辑推理和方程思想求出等腰三角形中的角的度数,让学生进一步巩固等腰三角形的性质1. 设计意图:让学生进一步巩固等腰三角形的性质1的同时,加强对等腰三角形性质2的运用,培养学生添加辅助线的能力. 设计意图:考查学生对等腰三角形性质1的掌握,运用等腰三角形性质1进行简单计算的能力. 设计意图:考查学生对等腰三角形性质1的掌握,和分类讨论的能力. 设计意图:考查学生对等腰三角形性质2的掌握,综合运用性质1和性质2解解决数学问题的能力.
板书设计 等腰三角形的性质1:等腰三角形的两个底角 相等 (简写成“等边对等角”). 等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高 相互重合 (简写成“三线合一”,注意:腰上的高和中线与底角的平分线不具有这一性质.).
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课是在学生已经学习了三角形的基本概念、全等三角形和轴对称知识的基础上,进一步研究特殊的三角形——等腰三角形、等腰三角形的性质为证明两个角相等、两条线段相等、两条直线垂直提供了方法,也是后续学习等边三角形、菱形、正方形、圆等内容的重要基础. 等腰三角形性质的探索是通过轴对称进行的,借助于轴对称发现了等腰三角形的性质,也获得了添加辅助线证明性质的方法.性质的证明是将欲证明相等的两个角(或线段)置于两个全等三角形之中,这是证明两个角相等或两条线段相等的基本策略之一.等腰三角形性质的探索与证明体现了转化的思想.
