【核心素养目标】数学人教版八年级上册14.1.3 积的乘方 教案 (表格式)
文档属性
| 名称 | 【核心素养目标】数学人教版八年级上册14.1.3 积的乘方 教案 (表格式) | 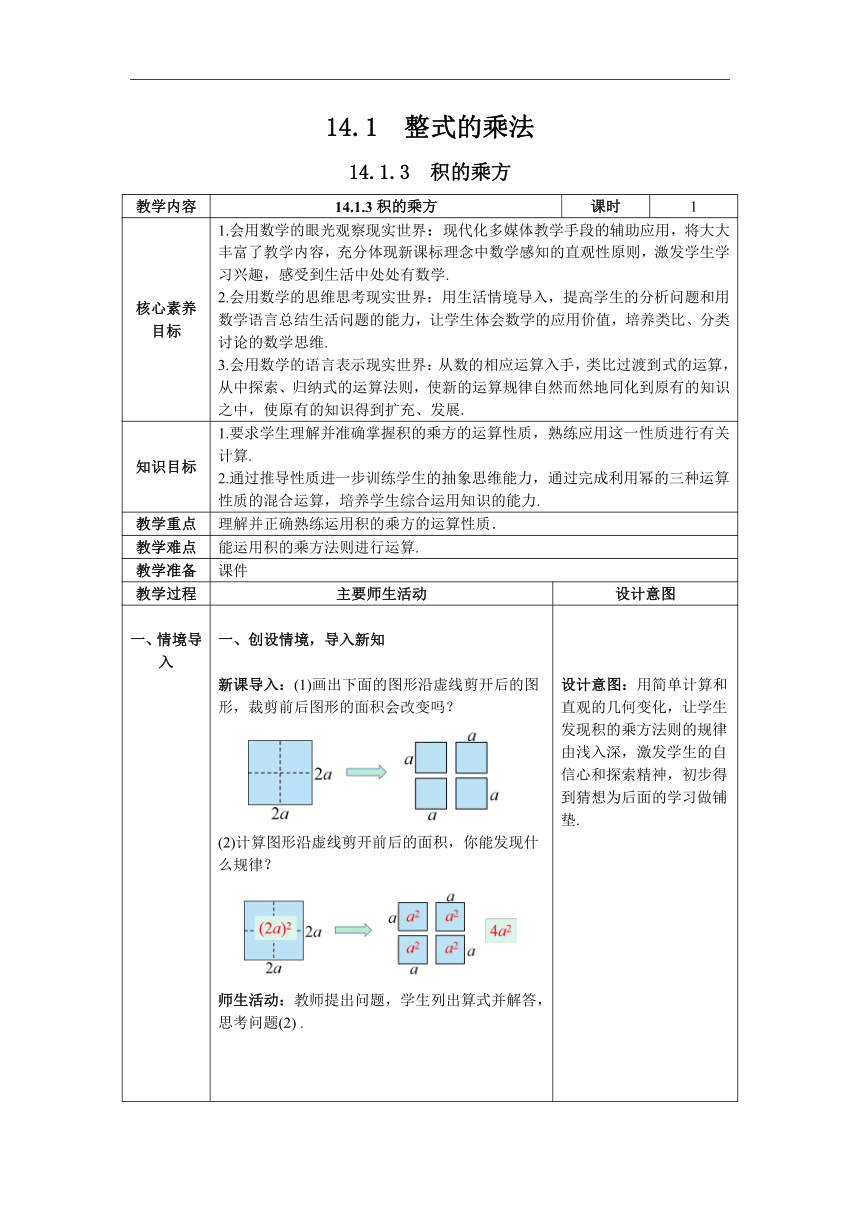 | |
| 格式 | docx | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 21:36:47 | ||
图片预览


文档简介
14.1 整式的乘法
14.1.3 积的乘方
教学内容 14.1.3积的乘方 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:现代化多媒体教学手段的辅助应用,将大大丰富了教学内容,充分体现新课标理念中数学感知的直观性原则,激发学生学习兴趣,感受到生活中处处有数学. 2.会用数学的思维思考现实世界:用生活情境导入,提高学生的分析问题和用数学语言总结生活问题的能力,让学生体会数学的应用价值,培养类比、分类讨论的数学思维. 3.会用数学的语言表示现实世界:从数的相应运算入手,类比过渡到式的运算,从中探索、归纳式的运算法则,使新的运算规律自然而然地同化到原有的知识之中,使原有的知识得到扩充、发展.
知识目标 1.要求学生理解并准确掌握积的乘方的运算性质,熟练应用这一性质进行有关计算. 2.通过推导性质进一步训练学生的抽象思维能力,通过完成利用幂的三种运算性质的混合运算,培养学生综合运用知识的能力.
教学重点 理解并正确熟练运用积的乘方的运算性质.
教学难点 能运用积的乘方法则进行运算.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 新课导入:(1)画出下面的图形沿虚线剪开后的图形,裁剪前后图形的面积会改变吗? (2)计算图形沿虚线剪开前后的面积,你能发现什么规律? 师生活动:教师提出问题,学生列出算式并解答,思考问题(2) . 二、小组合作,探究概念和性质 探究1:(1)计算下列各式. 观察两者有什么关系? (1)(2×3)2 =______; 22×32 =______ ; (2)(2×5)3 =______; 23×53 =______ ; (3)(3×5)2 =______; 32×52 =______ ; 师生活动:教师提出问题,学生带着问题完成填空. (2)观察三组式子的结果,我们得到三个等式:你发现了什么规律? 师生活动:学生独立思考并回答,教师总结猜想——积的乘方:等于把积的每一个因式分别 乘方 ,再把所得的幂 相乘 . (3)你能证明你的猜想吗? 师生活动:教师提出问题,学生先独立思考并写出推导过程,然后小组交流,学生代表展示推导过程: 一般地,对于任意底数a,b与任意正整数n , 追问2:通过上面的探索和推导,你能用文字语言概括出积的乘方的运算性质吗 师生活动:学生尝试用数学语言概括出积的乘方法则:(ab)n = a n b n. 教师引导学生完成文字说明:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘. 例1计算: ( 2a )3 ; (2) ( -5b )3 ; (3) ( xy2 )2 ; (4) ( -2x3 )4. 师生活动:师生共同分析解答,教师板书(1),学生板书(2)(3)(4).教师着重让学生说明底是什么,指数是什么,让学生注意计算时单项式的系数不要忘记乘方,以及要注意符号乘方的问题. 练习1.下列算式计算正确吗?如果不正确请写出正确答案. (1)(3x)3= 3x9; (2) (2ab)3 = 6a3b3 ; (3)(-3x2y2)3 = 27x6y6; (4) (-xy3)2 = x2y6. 师生活动:学生独立完成计算,并给出计算结果,在教师的引导下师生一起完成总结. 练习2.计算:(1) (-6ab)3; (2) -(3x2y)2; (3) (-3×102)3; (4) (-xny3m)2. 师生活动:学生回答,并相互补充.教师要重点提醒学生分析题目条件,能否应用积的乘方的运算性质以及如何正确应用. 例2 计算下列各式: (1) (2x2)3 + 2x·x5 - (-3x)2·x4; (2) -xy2 · (xy2)2 + (-2x2)3; (3) (-a3b6)2 + (-a2b4)3. 师生活动:师生共同分析解题步骤,学生独立解答,小组讨论后派代表给出答案. 想一想:根据积的乘方法则填空. 计算. (1) 82023×0.1252023 ; (2) (0.5)2023 ×(2)2024. 师生活动:学生独立解答,小组讨论后派代表给出答案. 练习 3. 计算:(0.25)4 ×(2)10. 师生活动:学生独立解答,学生代表板书,学生相互评价. 三、当堂练习,巩固所学 1. (武汉模拟) 计算 (4a2b3)2 的结果是( ) A. 6a4b5 B. 8a4b5 C. 12a4b5 D. 16a4b6 2. 判断正误: (1) (ab2)2 = ab4 ( ) (2) (2xy)4 = 8x4y4 ( ) (3) (-a2)2 = a4 ( ) (4) -(-ab2)2 = a2b4 ( ) 3. 计算: (1) 2(x3)2 · x3-(3x3)3 + (5x)2 · x7; (2) (3xy2)2 + (-4xy3) · (-xy). 4. 计算:(0.04)2023×[(-5)2023]2 设计意图:用简单计算和直观的几何变化,让学生发现积的乘方法则的规律由浅入深,激发学生的自信心和探索精神,初步得到猜想为后面的学习做铺垫. 设计意图:通过推导得出积的乘方的运算性质.让学生认识到,只有通过推理,才能最终确认结论.体验数式通性、从具体到抽象的思想方法对解决问题的价值. 设计意图:通过利用文字语言概括性质以及对性质进行推广的过程,促进学生对公式结构特征的深层理解. 设计意图:让学生运用性质进行计算,积累解题经验的,巩固对积的乘方法则的理解. 设计意图:让学生运用性质判断计算的正误,巩固积累解题经验. 设计意图:通过练习巩固积的乘方的运算性质. 设计意图:巩固积的乘方的运算性质,锻炼学生熟练地综合积的乘方的运算性质,整式的加减法运算性质进行混合运算的能力. 设计意图:对积的乘方运算性质的掌握情况,推广积的乘方的运算性质逆向运用的解题方法. 设计意图:锻炼学生根据积的乘方法则逆运用,将所求式子变形为已知式子,然后整体代换计算求值的能力. 设计意图:考查学生对积的乘方的运算性质的理解和应用. 设计意图:考查学生运用积的乘方的运算性质进行混合运算的计算能力. 设计意图:考查学生运用积的乘方的运算性质的逆向运用.
板书设计 14.1.3积的乘方 积的乘方:等于把积的每一个因式分别 乘方 ,再把所得的幂 相乘 .
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 这节课的重点是把握住积的乘方(ab)n = an bn(n是正整数)的使用范围:底数是积的乘方. 方法:把积的每一个因式分别乘方,再把所得的幂相乘. 在运用幂的运算法则时,注意知识拓展,底数和指数可以是数,也可以是整式,对三个以上因式的积也适用. 在运算的过程中要注意每一步依据,还应防止符号上的错误. 在建构新的法则时应注意前面学过的法则与新法则的区别和联系. 积的乘方是幂的第三个运算法则,也是整式乘法的基础,在内容处理上仍然先通过数字指数为例让学生计算,而后引导学生自主探索,讨论交流,归纳出一般指数情形的性质,即:概括出:(ab)n = an bn 尽可能让学生主动建构,获取新知,通过动脑、动口、动手提高自我总结能力,教学时引导学生关注每一步的根据. 不要把积的乘方性质与同底数幂的乘法性质混淆. 积的乘方运算,是转化为指数的乘法运算(底数不变);同底数幂的乘法,是转化为指数的加法运算(底数不变).同底数幂的乘法、积的乘方、积的乘方的三个运算性质是整式乘法的基础,也是整式乘法的主要依据. 对三个性质的数学表达式和语言表述,不仅要记住,更重要的是理解. 在这三个幂的运算中,要防止符号错误,还要防止运算性质发生混淆.
14.1.3 积的乘方
教学内容 14.1.3积的乘方 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:现代化多媒体教学手段的辅助应用,将大大丰富了教学内容,充分体现新课标理念中数学感知的直观性原则,激发学生学习兴趣,感受到生活中处处有数学. 2.会用数学的思维思考现实世界:用生活情境导入,提高学生的分析问题和用数学语言总结生活问题的能力,让学生体会数学的应用价值,培养类比、分类讨论的数学思维. 3.会用数学的语言表示现实世界:从数的相应运算入手,类比过渡到式的运算,从中探索、归纳式的运算法则,使新的运算规律自然而然地同化到原有的知识之中,使原有的知识得到扩充、发展.
知识目标 1.要求学生理解并准确掌握积的乘方的运算性质,熟练应用这一性质进行有关计算. 2.通过推导性质进一步训练学生的抽象思维能力,通过完成利用幂的三种运算性质的混合运算,培养学生综合运用知识的能力.
教学重点 理解并正确熟练运用积的乘方的运算性质.
教学难点 能运用积的乘方法则进行运算.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 新课导入:(1)画出下面的图形沿虚线剪开后的图形,裁剪前后图形的面积会改变吗? (2)计算图形沿虚线剪开前后的面积,你能发现什么规律? 师生活动:教师提出问题,学生列出算式并解答,思考问题(2) . 二、小组合作,探究概念和性质 探究1:(1)计算下列各式. 观察两者有什么关系? (1)(2×3)2 =______; 22×32 =______ ; (2)(2×5)3 =______; 23×53 =______ ; (3)(3×5)2 =______; 32×52 =______ ; 师生活动:教师提出问题,学生带着问题完成填空. (2)观察三组式子的结果,我们得到三个等式:你发现了什么规律? 师生活动:学生独立思考并回答,教师总结猜想——积的乘方:等于把积的每一个因式分别 乘方 ,再把所得的幂 相乘 . (3)你能证明你的猜想吗? 师生活动:教师提出问题,学生先独立思考并写出推导过程,然后小组交流,学生代表展示推导过程: 一般地,对于任意底数a,b与任意正整数n , 追问2:通过上面的探索和推导,你能用文字语言概括出积的乘方的运算性质吗 师生活动:学生尝试用数学语言概括出积的乘方法则:(ab)n = a n b n. 教师引导学生完成文字说明:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘. 例1计算: ( 2a )3 ; (2) ( -5b )3 ; (3) ( xy2 )2 ; (4) ( -2x3 )4. 师生活动:师生共同分析解答,教师板书(1),学生板书(2)(3)(4).教师着重让学生说明底是什么,指数是什么,让学生注意计算时单项式的系数不要忘记乘方,以及要注意符号乘方的问题. 练习1.下列算式计算正确吗?如果不正确请写出正确答案. (1)(3x)3= 3x9; (2) (2ab)3 = 6a3b3 ; (3)(-3x2y2)3 = 27x6y6; (4) (-xy3)2 = x2y6. 师生活动:学生独立完成计算,并给出计算结果,在教师的引导下师生一起完成总结. 练习2.计算:(1) (-6ab)3; (2) -(3x2y)2; (3) (-3×102)3; (4) (-xny3m)2. 师生活动:学生回答,并相互补充.教师要重点提醒学生分析题目条件,能否应用积的乘方的运算性质以及如何正确应用. 例2 计算下列各式: (1) (2x2)3 + 2x·x5 - (-3x)2·x4; (2) -xy2 · (xy2)2 + (-2x2)3; (3) (-a3b6)2 + (-a2b4)3. 师生活动:师生共同分析解题步骤,学生独立解答,小组讨论后派代表给出答案. 想一想:根据积的乘方法则填空. 计算. (1) 82023×0.1252023 ; (2) (0.5)2023 ×(2)2024. 师生活动:学生独立解答,小组讨论后派代表给出答案. 练习 3. 计算:(0.25)4 ×(2)10. 师生活动:学生独立解答,学生代表板书,学生相互评价. 三、当堂练习,巩固所学 1. (武汉模拟) 计算 (4a2b3)2 的结果是( ) A. 6a4b5 B. 8a4b5 C. 12a4b5 D. 16a4b6 2. 判断正误: (1) (ab2)2 = ab4 ( ) (2) (2xy)4 = 8x4y4 ( ) (3) (-a2)2 = a4 ( ) (4) -(-ab2)2 = a2b4 ( ) 3. 计算: (1) 2(x3)2 · x3-(3x3)3 + (5x)2 · x7; (2) (3xy2)2 + (-4xy3) · (-xy). 4. 计算:(0.04)2023×[(-5)2023]2 设计意图:用简单计算和直观的几何变化,让学生发现积的乘方法则的规律由浅入深,激发学生的自信心和探索精神,初步得到猜想为后面的学习做铺垫. 设计意图:通过推导得出积的乘方的运算性质.让学生认识到,只有通过推理,才能最终确认结论.体验数式通性、从具体到抽象的思想方法对解决问题的价值. 设计意图:通过利用文字语言概括性质以及对性质进行推广的过程,促进学生对公式结构特征的深层理解. 设计意图:让学生运用性质进行计算,积累解题经验的,巩固对积的乘方法则的理解. 设计意图:让学生运用性质判断计算的正误,巩固积累解题经验. 设计意图:通过练习巩固积的乘方的运算性质. 设计意图:巩固积的乘方的运算性质,锻炼学生熟练地综合积的乘方的运算性质,整式的加减法运算性质进行混合运算的能力. 设计意图:对积的乘方运算性质的掌握情况,推广积的乘方的运算性质逆向运用的解题方法. 设计意图:锻炼学生根据积的乘方法则逆运用,将所求式子变形为已知式子,然后整体代换计算求值的能力. 设计意图:考查学生对积的乘方的运算性质的理解和应用. 设计意图:考查学生运用积的乘方的运算性质进行混合运算的计算能力. 设计意图:考查学生运用积的乘方的运算性质的逆向运用.
板书设计 14.1.3积的乘方 积的乘方:等于把积的每一个因式分别 乘方 ,再把所得的幂 相乘 .
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 这节课的重点是把握住积的乘方(ab)n = an bn(n是正整数)的使用范围:底数是积的乘方. 方法:把积的每一个因式分别乘方,再把所得的幂相乘. 在运用幂的运算法则时,注意知识拓展,底数和指数可以是数,也可以是整式,对三个以上因式的积也适用. 在运算的过程中要注意每一步依据,还应防止符号上的错误. 在建构新的法则时应注意前面学过的法则与新法则的区别和联系. 积的乘方是幂的第三个运算法则,也是整式乘法的基础,在内容处理上仍然先通过数字指数为例让学生计算,而后引导学生自主探索,讨论交流,归纳出一般指数情形的性质,即:概括出:(ab)n = an bn 尽可能让学生主动建构,获取新知,通过动脑、动口、动手提高自我总结能力,教学时引导学生关注每一步的根据. 不要把积的乘方性质与同底数幂的乘法性质混淆. 积的乘方运算,是转化为指数的乘法运算(底数不变);同底数幂的乘法,是转化为指数的加法运算(底数不变).同底数幂的乘法、积的乘方、积的乘方的三个运算性质是整式乘法的基础,也是整式乘法的主要依据. 对三个性质的数学表达式和语言表述,不仅要记住,更重要的是理解. 在这三个幂的运算中,要防止符号错误,还要防止运算性质发生混淆.
