【核心素养目标】人教版数学七年级上册1.2.2 数轴 教案(表格式)
文档属性
| 名称 | 【核心素养目标】人教版数学七年级上册1.2.2 数轴 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览


文档简介
1.2 有理数
1.2.2 数轴
教学内容 1.2.2 数轴 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:让学生用几何符号表示实际问题,再将点用数表示,实现数学抽象,为定义数轴概念提供直观基础. 2.会用数学的思维思考现实世界:对学生渗透数形结合的重要思想方法. 3.会用数学的语言表示现实世界:使学生受到把实际问题抽象成数学问题的训练,逐步形成应用数学的意识;使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点.
知识目标 1. 掌握数轴的概念,理解数轴上的点和有理数的对应关系. 2. 会正确的画出数轴,利用数轴上的点表示有理数.
教学重点 掌握数轴的概念,理解数轴上的点和有理数的对应关系.
教学难点 会正确的画出数轴,利用数轴上的点表示有理数.
教学准备 课件.
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处分别有一棵柳树和一颗杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境. 师生活动: 分组讨论解决问题的方法,学生代表画图表示 追问1:马路可以用什么几何图形代表?(直线) 追问2:你认为站牌起到了什么作用?站牌、树、电线杆可以表示什么?(基准点)(直线上的点) 追问3:你是怎么确定问题中各物体的位置的 (方向与站牌的距离) 追问4:到站牌的方向与距离可以抽象成什么? (点的相对位置) 小组合作,探究概念和性质
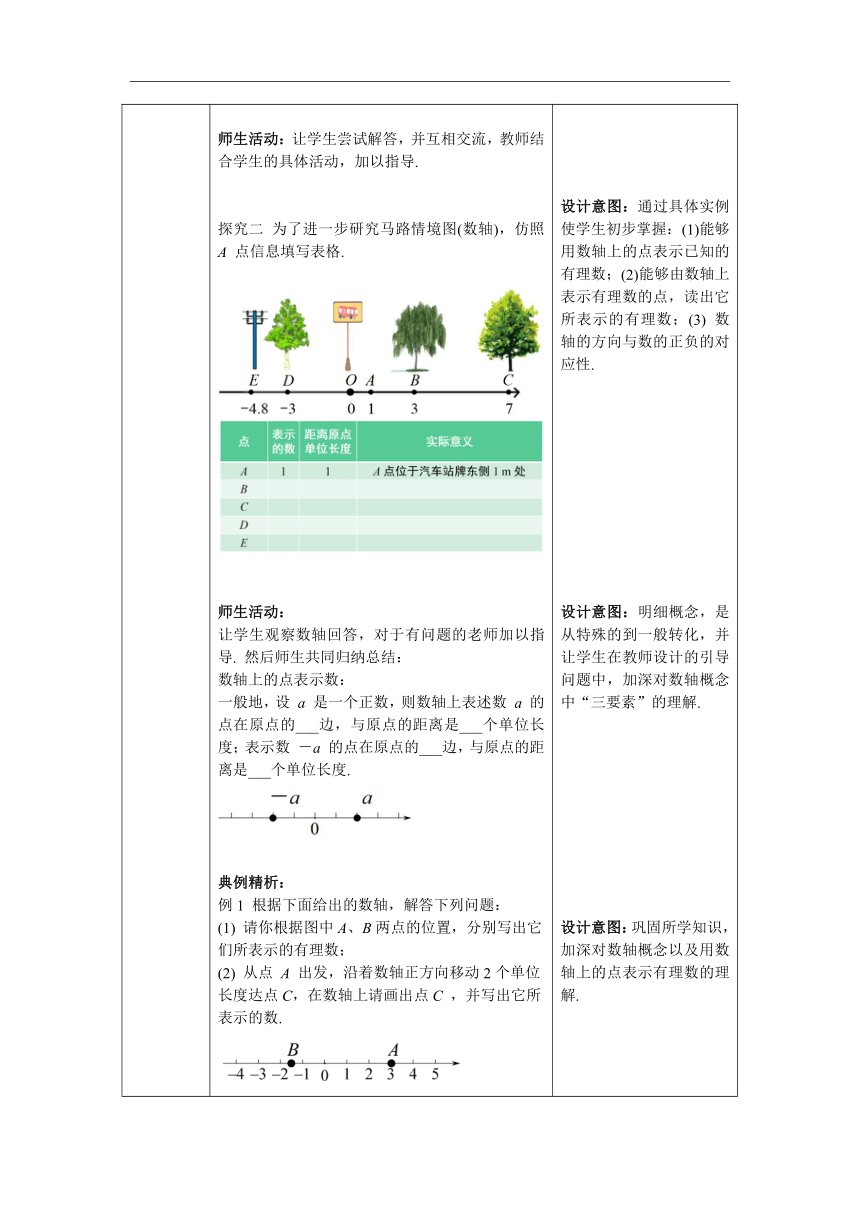
知识点一:数轴的画法及概念 探究一 怎样用数简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)? 师生活动: 学生画图表示后提问: 追问1: 0代表什么 (基准点) 追问1:数的符号的实际意义是什么 (方向) 追问3:上述方法表示了这些树、电线杆与汽车站牌的相对位围关系例如,-4.8表示位于汽车站牌西 侧4.8 m处的电线杆,你能再举个例子吗 合作探究: 你能联想到生活中的哪些用直线上的点表示数的工具,请举例说明. 师生活动:教师可以先解释0℃的含义(冰水混合物的温度规定为0℃一基准点) ,同理让学生仔细观看注射器和直尺的刻度. 追问:它们有什么共同特点? 师生活动:引导学生思索,进而给出数轴的定义. 同时引导学生探究共同得出数轴三要素 1.原点0——在直线上任意一点表示数“0” 2.正方向——通常取向右为正方向,画上箭头; 3.单位长度——选取适当的长度作为单位长度,单位长度要统一. 练一练: (松北区校级月考改编)关于数轴的图示,画法正确的是 ( ) 师生活动:让学生尝试解答,并互相交流,教师结合学生的具体活动,加以指导. 探究二 为了进一步研究马路情境图(数轴),仿照 A 点信息填写表格. 师生活动: 让学生观察数轴回答,对于有问题的老师加以指导. 然后师生共同归纳总结: 数轴上的点表示数: 一般地,设 a 是一个正数,则数轴上表述数 a 的点在原点的___边,与原点的距离是___个单位长度;表示数 -a 的点在原点的___边,与原点的距离是___个单位长度. 典例精析: 例1 根据下面给出的数轴,解答下列问题: (1) 请你根据图中A、B两点的位置,分别写出它们所表示的有理数; (2) 从点 A 出发,沿着数轴正方向移动2个单位长度达点C,在数轴上请画出点C ,并写出它所表示的数. 师生活动:教师应向学生强调,所有的有理数都可以在数轴. 上找个点与它对应,原点右边的点表示正数,原点左边的点表示负数. 数与数轴上的点结合,这是一种数形结合的重要数学思想. 练一练: 1.(滨州)在数轴上,点 A 表示-2 . 若从点 A 出发,沿数轴的正方向移动4个单位长度到达点 B,则点B表示的数是( ) A. -6 B. -4 C. 2 D. 4 2.(题1变式)点 A 表示数轴上的一个数,将点 A 向右平移 7 个单位长度,再向左平移 4 个单位长度,终点恰好是原点,则点 A 表示的数是_________. 师生活动: 1.两名学生板演,画出数轴解答,其余学生在练习本上做题. 2小组内批阅. 3.对板演的内容进行评价纠错. 三、当堂练习,巩固所学 1.在数轴上,原点及原点右边的点表示的数是( ) A. 正数 B. 负数 C. 非正数 D. 非负数 2.在数轴上表示 -3 的点与表示 4 的点之间的距离是( ) A. 7 B. -7 C. 1 D. -1 3. 画出数轴并表示下列有理数: 能力提升: 4.在数轴上,一只蚂蚁从原点出发,它先向右爬了4 个单位长度到达点 A,再向右爬了 2 个单位长度到达点 B,然后又向左爬了 10 个单位长度到达点 C. (1) 将 A,B,C 三点所表示的数在下图中的数轴上表示出来; (2) 根据点 C 在数轴上的位置,点 C 可以看作是蚂蚁从原点出发,向哪个方向爬了几个单位长度所到达的点 (3) 如果移动点 A,B,C 中的两个点,使得三个点重合,你有几种移动方法 请分别求出移动的长度之和. 拓展: 数轴上有两个固定点 A、B,有一动点 C ,请问点 C 在什么位置时,动点 C 到两定点距离之和最小 设计意图:“三要素”为定向,用直线、点、方向、距离等几何符号表示实际问题,这是实际问题的第一次数学抽象.
设计意图:继续以“三要素”为定向,将点用数表示,实现第二次抽象,为定义数轴概念提供直观基础. 设计意图:借用生活中的常用工具,说明正数、负数的作用,引导学生用“三要素”表达,为定义数轴概念提供又一个直观基础. 设计意图:复习巩固数轴的“三要素”. 设计意图:通过具体实例使学生初步掌握:(1)能够用数轴上的点表示已知的有理数;(2)能够由数轴上表示有理数的点,读出它所表示的有理数;(3) 数轴的方向与数的正负的对应性. 设计意图:明细概念,是从特殊的到一般转化,并让学生在教师设计的引导问题中,加深对数轴概念中“三要素”的理解. 设计意图:巩固所学知识,加深对数轴概念以及用数轴上的点表示有理数的理解. 设计意图:通过两道题的训练,使学生体会数轴上的点与有理数的对应的关系,并会规范地画出数轴. 设计意图:巩固所学知识,加深对数轴概念以及用数轴上的点表示有理数的理解. 设计意图:拓展用数轴上的两定点求解距离之和,就是求解移动的单位长度,注意分类讨论.
板书设计 数轴 数轴三要素: 原点; 2.正方向;3.单位长度
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 数轴是数形结合的基本知识,是学生难以理解的难点,教学过程应从贴近学生的实际出发,学生才易于接受和体验,让学生通过观察、思考和动手操作、经历数轴的形成过程,加深对数轴概念的理解,同时可培养抽象概括能力. 教学过程可突出“情境——抽象——概括”的主线,体现从特殊到一般研究问题的方法,注意从学生已有经验出发,发挥学生主体作用,会达到事半功倍的效果.
1.2.2 数轴
教学内容 1.2.2 数轴 课时 1
核心素养目标 1.会用数学的眼光观察现实世界:让学生用几何符号表示实际问题,再将点用数表示,实现数学抽象,为定义数轴概念提供直观基础. 2.会用数学的思维思考现实世界:对学生渗透数形结合的重要思想方法. 3.会用数学的语言表示现实世界:使学生受到把实际问题抽象成数学问题的训练,逐步形成应用数学的意识;使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点.
知识目标 1. 掌握数轴的概念,理解数轴上的点和有理数的对应关系. 2. 会正确的画出数轴,利用数轴上的点表示有理数.
教学重点 掌握数轴的概念,理解数轴上的点和有理数的对应关系.
教学难点 会正确的画出数轴,利用数轴上的点表示有理数.
教学准备 课件.
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处分别有一棵柳树和一颗杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境. 师生活动: 分组讨论解决问题的方法,学生代表画图表示 追问1:马路可以用什么几何图形代表?(直线) 追问2:你认为站牌起到了什么作用?站牌、树、电线杆可以表示什么?(基准点)(直线上的点) 追问3:你是怎么确定问题中各物体的位置的 (方向与站牌的距离) 追问4:到站牌的方向与距离可以抽象成什么? (点的相对位置) 小组合作,探究概念和性质
知识点一:数轴的画法及概念 探究一 怎样用数简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)? 师生活动: 学生画图表示后提问: 追问1: 0代表什么 (基准点) 追问1:数的符号的实际意义是什么 (方向) 追问3:上述方法表示了这些树、电线杆与汽车站牌的相对位围关系例如,-4.8表示位于汽车站牌西 侧4.8 m处的电线杆,你能再举个例子吗 合作探究: 你能联想到生活中的哪些用直线上的点表示数的工具,请举例说明. 师生活动:教师可以先解释0℃的含义(冰水混合物的温度规定为0℃一基准点) ,同理让学生仔细观看注射器和直尺的刻度. 追问:它们有什么共同特点? 师生活动:引导学生思索,进而给出数轴的定义. 同时引导学生探究共同得出数轴三要素 1.原点0——在直线上任意一点表示数“0” 2.正方向——通常取向右为正方向,画上箭头; 3.单位长度——选取适当的长度作为单位长度,单位长度要统一. 练一练: (松北区校级月考改编)关于数轴的图示,画法正确的是 ( ) 师生活动:让学生尝试解答,并互相交流,教师结合学生的具体活动,加以指导. 探究二 为了进一步研究马路情境图(数轴),仿照 A 点信息填写表格. 师生活动: 让学生观察数轴回答,对于有问题的老师加以指导. 然后师生共同归纳总结: 数轴上的点表示数: 一般地,设 a 是一个正数,则数轴上表述数 a 的点在原点的___边,与原点的距离是___个单位长度;表示数 -a 的点在原点的___边,与原点的距离是___个单位长度. 典例精析: 例1 根据下面给出的数轴,解答下列问题: (1) 请你根据图中A、B两点的位置,分别写出它们所表示的有理数; (2) 从点 A 出发,沿着数轴正方向移动2个单位长度达点C,在数轴上请画出点C ,并写出它所表示的数. 师生活动:教师应向学生强调,所有的有理数都可以在数轴. 上找个点与它对应,原点右边的点表示正数,原点左边的点表示负数. 数与数轴上的点结合,这是一种数形结合的重要数学思想. 练一练: 1.(滨州)在数轴上,点 A 表示-2 . 若从点 A 出发,沿数轴的正方向移动4个单位长度到达点 B,则点B表示的数是( ) A. -6 B. -4 C. 2 D. 4 2.(题1变式)点 A 表示数轴上的一个数,将点 A 向右平移 7 个单位长度,再向左平移 4 个单位长度,终点恰好是原点,则点 A 表示的数是_________. 师生活动: 1.两名学生板演,画出数轴解答,其余学生在练习本上做题. 2小组内批阅. 3.对板演的内容进行评价纠错. 三、当堂练习,巩固所学 1.在数轴上,原点及原点右边的点表示的数是( ) A. 正数 B. 负数 C. 非正数 D. 非负数 2.在数轴上表示 -3 的点与表示 4 的点之间的距离是( ) A. 7 B. -7 C. 1 D. -1 3. 画出数轴并表示下列有理数: 能力提升: 4.在数轴上,一只蚂蚁从原点出发,它先向右爬了4 个单位长度到达点 A,再向右爬了 2 个单位长度到达点 B,然后又向左爬了 10 个单位长度到达点 C. (1) 将 A,B,C 三点所表示的数在下图中的数轴上表示出来; (2) 根据点 C 在数轴上的位置,点 C 可以看作是蚂蚁从原点出发,向哪个方向爬了几个单位长度所到达的点 (3) 如果移动点 A,B,C 中的两个点,使得三个点重合,你有几种移动方法 请分别求出移动的长度之和. 拓展: 数轴上有两个固定点 A、B,有一动点 C ,请问点 C 在什么位置时,动点 C 到两定点距离之和最小 设计意图:“三要素”为定向,用直线、点、方向、距离等几何符号表示实际问题,这是实际问题的第一次数学抽象.
设计意图:继续以“三要素”为定向,将点用数表示,实现第二次抽象,为定义数轴概念提供直观基础. 设计意图:借用生活中的常用工具,说明正数、负数的作用,引导学生用“三要素”表达,为定义数轴概念提供又一个直观基础. 设计意图:复习巩固数轴的“三要素”. 设计意图:通过具体实例使学生初步掌握:(1)能够用数轴上的点表示已知的有理数;(2)能够由数轴上表示有理数的点,读出它所表示的有理数;(3) 数轴的方向与数的正负的对应性. 设计意图:明细概念,是从特殊的到一般转化,并让学生在教师设计的引导问题中,加深对数轴概念中“三要素”的理解. 设计意图:巩固所学知识,加深对数轴概念以及用数轴上的点表示有理数的理解. 设计意图:通过两道题的训练,使学生体会数轴上的点与有理数的对应的关系,并会规范地画出数轴. 设计意图:巩固所学知识,加深对数轴概念以及用数轴上的点表示有理数的理解. 设计意图:拓展用数轴上的两定点求解距离之和,就是求解移动的单位长度,注意分类讨论.
板书设计 数轴 数轴三要素: 原点; 2.正方向;3.单位长度
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 数轴是数形结合的基本知识,是学生难以理解的难点,教学过程应从贴近学生的实际出发,学生才易于接受和体验,让学生通过观察、思考和动手操作、经历数轴的形成过程,加深对数轴概念的理解,同时可培养抽象概括能力. 教学过程可突出“情境——抽象——概括”的主线,体现从特殊到一般研究问题的方法,注意从学生已有经验出发,发挥学生主体作用,会达到事半功倍的效果.
