【核心素养目标】人教版 数学七年级上册1.2.4 第1课时 绝对值 教案(表格式)
文档属性
| 名称 | 【核心素养目标】人教版 数学七年级上册1.2.4 第1课时 绝对值 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 258.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 22:41:06 | ||
图片预览


文档简介
1.2.4 绝对值
第 1 课时 绝对值
教学内容 第 1 课时 绝对值 课时 1
核心素养目标 会用数学的眼光观察现实世界:感悟数学的审美价值形成对数学的好奇心与想象力,主动参与数学探究活动,发展创新意识. 会用数学的思维思考现实世界:通过数轴使学生经历实践、观察、思考的过程,和教师一起建构有理数的绝对值的定义,直观地理解绝对值的概念. 3.会用数学的语言表示现实世界:通过数形转化的模型理解绝对值概念的几何意义.
知识目标 1. 理解绝对值的概念及性质; 2. 会求一个有理数的绝对值.
教学重点 理解绝对值的概念及性质.
教学难点 理解绝对值的概念及性质.
教学准备 课件.
教学过程 主要师生活动 设计意图
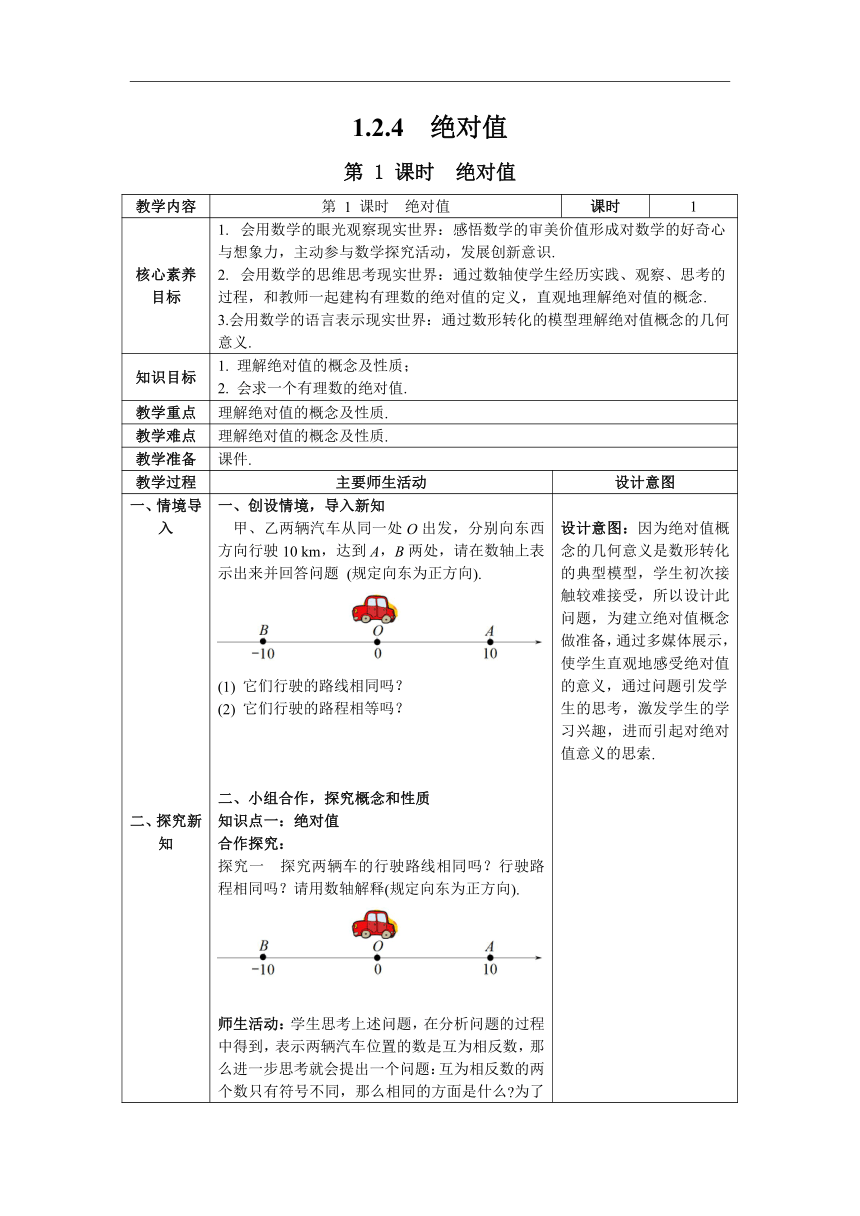
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 甲、乙两辆汽车从同一处O出发,分别向东西方向行驶10 km,达到A,B两处,请在数轴上表示出来并回答问题 (规定向东为正方向). (1) 它们行驶的路线相同吗? (2) 它们行驶的路程相等吗? 小组合作,探究概念和性质
知识点一:绝对值 合作探究: 探究一 探究两辆车的行驶路线相同吗?行驶路程相同吗?请用数轴解释(规定向东为正方向). 师生活动:学生思考上述问题,在分析问题的过程中得到,表示两辆汽车位置的数是互为相反数,那 么进一步思考就会提出一个问题:互为相反数的两个数只有符号不同,那么相同的方面是什么 为了解决这一问题,先请同学们观察两个点的位置关系,并请同学在讨论后说出它们的位置关系. 学生小组内交流:位置关系是两个点分别在原点的两侧,两个点到原点的距离相等或者说两个点到原 点有相同倍的单位长度. 教师引出新课:两个点到原点的距离相等表明相应的有理数具有什么样的性质呢?今天我们就来研究这个问题. 绝对值的定义: 一般地,数轴上表示数 a 的点与原点的距离叫做数a 的绝对值,记作 | a |. 教材挖掘: 例:因为点 A 表示10,与原点的距离是 10 个单位长度, 所以 | 10 | = 10. 师生活动:这样我们就进一步明确一个数是由它的符号和绝对值两部分组成. 教师强调:这里的数a可以是正数、负数和0. 练一练: 利用数轴,口答下列问题: 师生活动:学生根据绝对值的定义直接求出各数的绝对值,然后观察每个问题中的绝对值符号内的数和相应的结果之间的关系,进行归纳、总结. 探究二 对于任意数 a,你能求出它的绝对值? 师生活动:教师引导学生确定数轴上a的位置是需要考虑a 的正负性,需要分类讨论. 然后共同归纳总结: 数学语言: 当a > 0时,| a | =_____ ; 当a < 0时,| a | =_____ ; 当a = 0时,| a | =______. 总结:一个正数的绝对值是它______;一个负数的绝对值是它的_______;0 的绝对值是_____. 练一练: 写出下列各数的相反数: |-(+5)|、|-(-3.5)|、|-(-)|、|-(-(- ) )| 3. 已知 | x-4 |+| y-3 | = 0,求 x + y 的值. 三、当堂练习,巩固所学 1. 判断对错: (1) 一个数的绝对值等于本身,则该数一定是正数; ( ) (2) 一个数的绝对值等于它的相反数,这个数一定是负数; ( ) (3) 如果两个数的绝对值相等,那么这两个数一定 相等; ( ) (4) 如果两个数不相等,那么这两个数的绝对值 一定不等;( ) (5) 有理数的绝对值一定是非负数.( ) 2. 化简: | 0 | = ; | x | = (x<0); | m – n | = (m>n). 3. 某工厂生产一批螺帽,根据产品质量要求,螺帽的内径可以有 0.02 毫米的误差,抽查 5 只螺帽,超过规定内径的毫米数记作正数,不足规定内径的毫米数记作负数,检查结果如下表: (1) 根据调查结果,指出哪些产品是合乎要求的(即在误差范围内的); (2) 指出合乎要求的产品中哪一个质量好一些,并用绝对值的知识说明. 设计意图:因为绝对值概念的几何意义是数形转化的典型模型,学生初次接触较难接受,所以设计此问题,为建立绝对值概念做准备,通过多媒体展示,使学生直观地感受绝对值的意义,通过问题引发学 生的思考,激发学生的学习兴趣,进而引起对绝对值意义的思索.
设计意图:绝对值的概念是一个主要概念,也是一个难点,通过数轴使学生经历实践、观察、思考的过程,和教师一起建构有理数的绝对值的定义,直观地理解绝对值的概念. 设计意图:通过数形结合的形式更能直观的理解绝对值的代数含义,同时为后面学习“用字母代表数”作铺垫. 设计意图:由已知一个数会求其绝对值到已知一个数的绝对值求这个数,通过进行逆向思维训练,培养思维的灵活性和深刻性. 设计意图:通过练习使学生对绝对值的概念和求绝对值的方法及时得到巩固,强化基本概念的落实, 进而突破难点.
板书设计 绝对值 数学语言: 当a > 0时,| a | =_____ ; 当a < 0时,| a | =_____ ; 当a = 0时,| a | =______.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 课时应从生活中的实际问题出发,引导学生探索绝对值的概念、表示方法,根据绝对值的意义会求一个数的绝对值,通过观察和分析知道一个数的绝对值会求这个数.教学中,以问题为载体给学生提供探索的空间,强调学生的自主学习和小组交流,在形成一定的认识后,教师出示相应习题,指导学生完成以巩固所学知识.
第 1 课时 绝对值
教学内容 第 1 课时 绝对值 课时 1
核心素养目标 会用数学的眼光观察现实世界:感悟数学的审美价值形成对数学的好奇心与想象力,主动参与数学探究活动,发展创新意识. 会用数学的思维思考现实世界:通过数轴使学生经历实践、观察、思考的过程,和教师一起建构有理数的绝对值的定义,直观地理解绝对值的概念. 3.会用数学的语言表示现实世界:通过数形转化的模型理解绝对值概念的几何意义.
知识目标 1. 理解绝对值的概念及性质; 2. 会求一个有理数的绝对值.
教学重点 理解绝对值的概念及性质.
教学难点 理解绝对值的概念及性质.
教学准备 课件.
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 甲、乙两辆汽车从同一处O出发,分别向东西方向行驶10 km,达到A,B两处,请在数轴上表示出来并回答问题 (规定向东为正方向). (1) 它们行驶的路线相同吗? (2) 它们行驶的路程相等吗? 小组合作,探究概念和性质
知识点一:绝对值 合作探究: 探究一 探究两辆车的行驶路线相同吗?行驶路程相同吗?请用数轴解释(规定向东为正方向). 师生活动:学生思考上述问题,在分析问题的过程中得到,表示两辆汽车位置的数是互为相反数,那 么进一步思考就会提出一个问题:互为相反数的两个数只有符号不同,那么相同的方面是什么 为了解决这一问题,先请同学们观察两个点的位置关系,并请同学在讨论后说出它们的位置关系. 学生小组内交流:位置关系是两个点分别在原点的两侧,两个点到原点的距离相等或者说两个点到原 点有相同倍的单位长度. 教师引出新课:两个点到原点的距离相等表明相应的有理数具有什么样的性质呢?今天我们就来研究这个问题. 绝对值的定义: 一般地,数轴上表示数 a 的点与原点的距离叫做数a 的绝对值,记作 | a |. 教材挖掘: 例:因为点 A 表示10,与原点的距离是 10 个单位长度, 所以 | 10 | = 10. 师生活动:这样我们就进一步明确一个数是由它的符号和绝对值两部分组成. 教师强调:这里的数a可以是正数、负数和0. 练一练: 利用数轴,口答下列问题: 师生活动:学生根据绝对值的定义直接求出各数的绝对值,然后观察每个问题中的绝对值符号内的数和相应的结果之间的关系,进行归纳、总结. 探究二 对于任意数 a,你能求出它的绝对值? 师生活动:教师引导学生确定数轴上a的位置是需要考虑a 的正负性,需要分类讨论. 然后共同归纳总结: 数学语言: 当a > 0时,| a | =_____ ; 当a < 0时,| a | =_____ ; 当a = 0时,| a | =______. 总结:一个正数的绝对值是它______;一个负数的绝对值是它的_______;0 的绝对值是_____. 练一练: 写出下列各数的相反数: |-(+5)|、|-(-3.5)|、|-(-)|、|-(-(- ) )| 3. 已知 | x-4 |+| y-3 | = 0,求 x + y 的值. 三、当堂练习,巩固所学 1. 判断对错: (1) 一个数的绝对值等于本身,则该数一定是正数; ( ) (2) 一个数的绝对值等于它的相反数,这个数一定是负数; ( ) (3) 如果两个数的绝对值相等,那么这两个数一定 相等; ( ) (4) 如果两个数不相等,那么这两个数的绝对值 一定不等;( ) (5) 有理数的绝对值一定是非负数.( ) 2. 化简: | 0 | = ; | x | = (x<0); | m – n | = (m>n). 3. 某工厂生产一批螺帽,根据产品质量要求,螺帽的内径可以有 0.02 毫米的误差,抽查 5 只螺帽,超过规定内径的毫米数记作正数,不足规定内径的毫米数记作负数,检查结果如下表: (1) 根据调查结果,指出哪些产品是合乎要求的(即在误差范围内的); (2) 指出合乎要求的产品中哪一个质量好一些,并用绝对值的知识说明. 设计意图:因为绝对值概念的几何意义是数形转化的典型模型,学生初次接触较难接受,所以设计此问题,为建立绝对值概念做准备,通过多媒体展示,使学生直观地感受绝对值的意义,通过问题引发学 生的思考,激发学生的学习兴趣,进而引起对绝对值意义的思索.
设计意图:绝对值的概念是一个主要概念,也是一个难点,通过数轴使学生经历实践、观察、思考的过程,和教师一起建构有理数的绝对值的定义,直观地理解绝对值的概念. 设计意图:通过数形结合的形式更能直观的理解绝对值的代数含义,同时为后面学习“用字母代表数”作铺垫. 设计意图:由已知一个数会求其绝对值到已知一个数的绝对值求这个数,通过进行逆向思维训练,培养思维的灵活性和深刻性. 设计意图:通过练习使学生对绝对值的概念和求绝对值的方法及时得到巩固,强化基本概念的落实, 进而突破难点.
板书设计 绝对值 数学语言: 当a > 0时,| a | =_____ ; 当a < 0时,| a | =_____ ; 当a = 0时,| a | =______.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 课时应从生活中的实际问题出发,引导学生探索绝对值的概念、表示方法,根据绝对值的意义会求一个数的绝对值,通过观察和分析知道一个数的绝对值会求这个数.教学中,以问题为载体给学生提供探索的空间,强调学生的自主学习和小组交流,在形成一定的认识后,教师出示相应习题,指导学生完成以巩固所学知识.
