【核心素养目标】人教版数学七年级上册4.3.2 角的比较与运算 教案 (表格式)
文档属性
| 名称 | 【核心素养目标】人教版数学七年级上册4.3.2 角的比较与运算 教案 (表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 546.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览



文档简介
4.3 角
4.3.2 角的比较与运算
教学内容 4.3.2 角的比较与运算 课时 1
核心素养目标 会用数学的眼光观察世界:学会应用几何模型,能结合几何模型或身边环境,指出角. 会用数学的思维思考问题:通过类比学习,提升学生的迁移能力,不同切入点思考,助力学生养成谨慎思考的习惯. 会用数学的语言表达思想:培意识到几何语言中任何一种表述方式一定要准确唯一,使学生认识数学语言的严谨性;但一个对象可以用不同的方式表示,体会数学语言的多样性.
知识目标 1. 掌握角的大小的比较方法. 2. 理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题. 3. 会进行涉及度、分、秒的角度的计算.
教学重点 掌握角的大小的比较方法,理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述.
教学难点 能够解答角平分线和角的和、差、倍、分有关的问题,会进行涉及度、分、秒的角度的计算.
教学准备 课件、纸片
教学过程 主要师生活动 设计意图
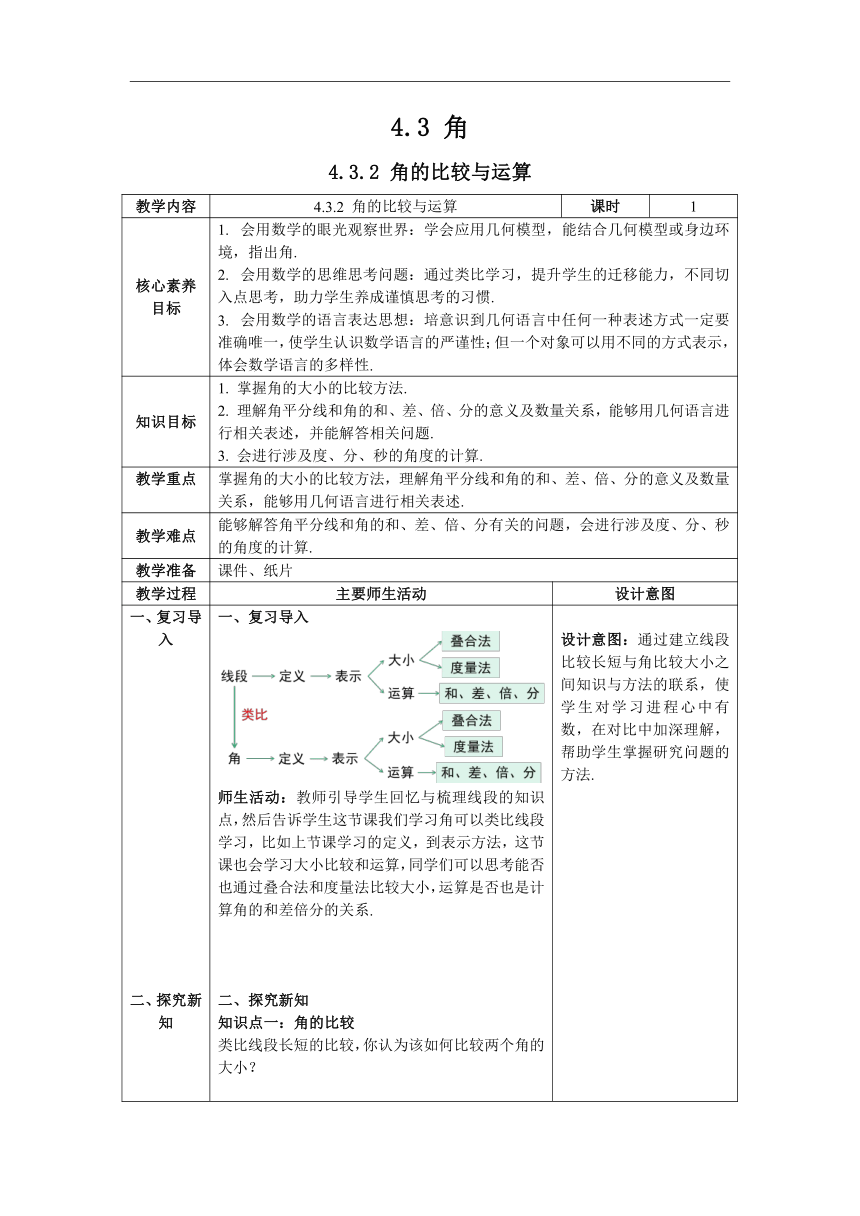
一、复习导入 二、探究新知 当堂练习 一、复习导入 师生活动:教师引导学生回忆与梳理线段的知识点,然后告诉学生这节课我们学习角可以类比线段学习,比如上节课学习的定义,到表示方法,这节课也会学习大小比较和运算,同学们可以思考能否也通过叠合法和度量法比较大小,运算是否也是计算角的和差倍分的关系. 二、探究新知 知识点一:角的比较 类比线段长短的比较,你认为该如何比较两个角的大小? 师生活动:学生先自主思考并小组交流,再由小组代表发言,预测会有两种方法,度量法和叠合法.教师引导和规范学生操作步骤,得出结果如下: 度量法: 因为 55°>40°,所以∠1>∠2. 叠合法: 想一想:你能用图形和几何语言说明两个角的大小关系吗 (两个角分别记作∠AOB,∠A'O'B' )? 师生活动:学生画出图形,并用符号表示,指出两个角的大小关系有且仅有三种情况. 知识点二:角的运算 探究1:如图,图中共有几个角?它们之间有什么关系? 师生活动: 预测学生能确定角的个数,明确角之间的和差关系如下: 3个:∠AOB、∠AOC、∠BOC ∠AOC =∠AOB +∠BOC ∠AOB =∠AOC -∠BOC ∠BOC =∠AOC -∠AOB 教师关注学生是否能发现角的和差关系,教师可引导学生类比线段的和与差,发现角的和差关系. 然后教师引导学生总结:共顶点的几个角,可进行加减. 探究2 :如图,借助三角尺画出15°,75°的角.用一副三角尺,你还能画出哪些度数的角?试一试. 师生活动:学生动手操作,小组合作探究,师生归纳,如下: 用三角尺画特殊角,关键在于把它写成30°,45°,60°,90°角的和或差. 凡是15的整数倍的角,都能用三角尺画出,而能用三角尺画出的,也只限于这样的角. 例题精析: 例1 如图,O是直线AB上一点,∠AOC = 53°17′,求∠BOC的度数. 师生活动:学生独立思考,请学生代表发言,教师予以适当的评价并整理板书. 解:由题意可知,∠AOB是平角, ∠AOB =∠AOC +∠BOC 所以∠BOC =∠AOB -∠AOC = 180° - 53°17′ = 126°43′ 总结: ①同单位加减(度与度、分与分、秒与秒分别相加、减); ②度分秒是60进制(相加时逢60要进位,相减时要借1作60). 师生活动:教师引导学生思考与总结解题思路与过程. 例2 把一个周角7等分,每一份是多少度的角 (精确到分)? 师生活动:学生独立思考,由学生代表发言,教师与学生共同完成板书: 解:360°÷7 = 51°+ 3°÷7 = 51° + 180′÷7 ≈ 51°26′ 答:每份是 51°26′的角. 教师引导学生总结:注意度、分、秒是60进制的,要把剩余的度数化成分. 探究3:你能在∠AOC内找一条射线OB,使∠AOB =∠BOC吗? 师生活动:教师提问,学生自主思考,教师巡堂指导,预测会有不同方法,教师可让这些学生代表分别展示,预测两种方法(如下): 对折法: 度量法: 教师追问:同学们知道图中三个角的数量关系吗? 学生思考,学生代表回答,师生共同总结与填空. 教师再以此引出角平分线的定义. 定义总结: 师生活动:教师讲解,再让学生朗读定义,加深印象. 类比:仿照角平分线的结论,你能写出角的三等分线的结论吗? 师生活动:学生独立思考,由学生代表发言,教师予以适当评价,帮助学生正确规范完成几何书写. 例3 如图OC是∠AOB的平分线,OB是∠COD的三等平分线,∠BOD = 15°.则∠AOB等于 ( ) A. 75 B. 70 C. 65 D. 60 师生活动:学生独立思考,学生代表发言,教师适时评价与引导. 思考:除此题所给图片的情况,你还能想出其他情况与答案吗? 师生活动:学生独立思考,学生代表上台展示,教师予以评价与指导,得出另一种结果,∠AOB = 15°. 三、当堂练习 1. 比较大小:60°25′ 60.25°(填“>”,“<” 或“=”). 2. 计算: (1) 180° - 98°24′30″ (2) 62°24′17″×4 3. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOB = 50°,∠DOE = 30°,那么∠BOD是多少度? 设计意图:通过建立线段比较长短与角比较大小之间知识与方法的联系,使学生对学习进程心中有数,在对比中加深理解,帮助学生掌握研究问题的方法. 设计意图:采用类比的方法,按照“几何模型--图形--文字--符号”的学习程序,学生动手操作,自主探究. 设计意图:指出对于两个角的大小关系和两个实数的大小关系一样,有且仅有三种情况: ∠AOB <∠A′O′B′, ∠AOB =∠A′O′B′, ∠AOB>∠A′O′B′, 为以后分类研究一些有关角的问题奠定基础. 设计意图:针对同一图形变换审视角度提出问题,可以提高学生的读图能力,用符号表示角的和差关系,仍遵循“几何模型——图形——文字——符号”的学习过程,在图形与等式之间建立一种关系. 设计意图:用一副三角尺画出一些特殊角,除让学生巩固角的和与差概念外,也使学生对这些特殊角的大小有直观的认识,培养对角的大小的估计能力和动手操作能力,加深学生对角的认识. 设计意图:通过题目锻炼学生运算能力,初步学习几何语言在解题中的运用,体会几何与代数之间的联系与不同,加深学生的数形结合思想. 设计意图:从角的和差问题中,将射线OB的位置特殊化,并类比线段的中点,引出角的平分线的概念,不仅知识的产生、发展自然连续,也体现了由一般到特殊,由特殊到一般的研究方法,同时,也能建立知识间的联系,完善认知结构. 设计意图:进一步明晰角平分线的概念,为后续学习轴对称和研究有关图形的翻折问题打下基础. 设计意图:通过类比让学生学会举一反三,体会几何知识的关联性,巩固几何语言的书写. 设计意图:通过题目帮助学生巩固角平分线的知识与角的运算,提高学生的识图能力和运算能力. 又通过思考题启发学生思考其他可能性,建立分类讨论思想,养成严谨思考的习惯. 设计意图:通过练习巩固角的大小比较. 设计意图:通过练习巩固角度的运算. 设计意图:通过练习强化试图能力和运算能力.
板书设计 4.3.2 角的比较与运算 角的概念 角的表示 角的度量和单位
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 数形结合,培养识图能力 角的比较大小、角的和与差、角平分线研究与研究线段的大小比较、和与差、中点的内容和方法很相似,教学时把两者作对比,学生在学习方法和学习内容的理解上,不会有困难.困难在于正确地完成图形语言、文字语言、符号语言之间的转化,究其原因,一方面,语言是思维的产物,图形是实物和模型第一次抽象,是对研究对象的直观反映,文字语言是对图形的描述、理解和讨论,符号语言则是对文字语言的简化和再次抽象.它们的综合运用,要求学生必须对研究对象从数和形上有着深刻的理解,并具有读图和画图的能力;二是需要培养和训练,对于图形、文字、符号语言的综合运用,虽然在学习线段知识时已有接触,但要达到融会贯通的程度还需要经过一段时间的学习和训练.
4.3.2 角的比较与运算
教学内容 4.3.2 角的比较与运算 课时 1
核心素养目标 会用数学的眼光观察世界:学会应用几何模型,能结合几何模型或身边环境,指出角. 会用数学的思维思考问题:通过类比学习,提升学生的迁移能力,不同切入点思考,助力学生养成谨慎思考的习惯. 会用数学的语言表达思想:培意识到几何语言中任何一种表述方式一定要准确唯一,使学生认识数学语言的严谨性;但一个对象可以用不同的方式表示,体会数学语言的多样性.
知识目标 1. 掌握角的大小的比较方法. 2. 理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题. 3. 会进行涉及度、分、秒的角度的计算.
教学重点 掌握角的大小的比较方法,理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述.
教学难点 能够解答角平分线和角的和、差、倍、分有关的问题,会进行涉及度、分、秒的角度的计算.
教学准备 课件、纸片
教学过程 主要师生活动 设计意图
一、复习导入 二、探究新知 当堂练习 一、复习导入 师生活动:教师引导学生回忆与梳理线段的知识点,然后告诉学生这节课我们学习角可以类比线段学习,比如上节课学习的定义,到表示方法,这节课也会学习大小比较和运算,同学们可以思考能否也通过叠合法和度量法比较大小,运算是否也是计算角的和差倍分的关系. 二、探究新知 知识点一:角的比较 类比线段长短的比较,你认为该如何比较两个角的大小? 师生活动:学生先自主思考并小组交流,再由小组代表发言,预测会有两种方法,度量法和叠合法.教师引导和规范学生操作步骤,得出结果如下: 度量法: 因为 55°>40°,所以∠1>∠2. 叠合法: 想一想:你能用图形和几何语言说明两个角的大小关系吗 (两个角分别记作∠AOB,∠A'O'B' )? 师生活动:学生画出图形,并用符号表示,指出两个角的大小关系有且仅有三种情况. 知识点二:角的运算 探究1:如图,图中共有几个角?它们之间有什么关系? 师生活动: 预测学生能确定角的个数,明确角之间的和差关系如下: 3个:∠AOB、∠AOC、∠BOC ∠AOC =∠AOB +∠BOC ∠AOB =∠AOC -∠BOC ∠BOC =∠AOC -∠AOB 教师关注学生是否能发现角的和差关系,教师可引导学生类比线段的和与差,发现角的和差关系. 然后教师引导学生总结:共顶点的几个角,可进行加减. 探究2 :如图,借助三角尺画出15°,75°的角.用一副三角尺,你还能画出哪些度数的角?试一试. 师生活动:学生动手操作,小组合作探究,师生归纳,如下: 用三角尺画特殊角,关键在于把它写成30°,45°,60°,90°角的和或差. 凡是15的整数倍的角,都能用三角尺画出,而能用三角尺画出的,也只限于这样的角. 例题精析: 例1 如图,O是直线AB上一点,∠AOC = 53°17′,求∠BOC的度数. 师生活动:学生独立思考,请学生代表发言,教师予以适当的评价并整理板书. 解:由题意可知,∠AOB是平角, ∠AOB =∠AOC +∠BOC 所以∠BOC =∠AOB -∠AOC = 180° - 53°17′ = 126°43′ 总结: ①同单位加减(度与度、分与分、秒与秒分别相加、减); ②度分秒是60进制(相加时逢60要进位,相减时要借1作60). 师生活动:教师引导学生思考与总结解题思路与过程. 例2 把一个周角7等分,每一份是多少度的角 (精确到分)? 师生活动:学生独立思考,由学生代表发言,教师与学生共同完成板书: 解:360°÷7 = 51°+ 3°÷7 = 51° + 180′÷7 ≈ 51°26′ 答:每份是 51°26′的角. 教师引导学生总结:注意度、分、秒是60进制的,要把剩余的度数化成分. 探究3:你能在∠AOC内找一条射线OB,使∠AOB =∠BOC吗? 师生活动:教师提问,学生自主思考,教师巡堂指导,预测会有不同方法,教师可让这些学生代表分别展示,预测两种方法(如下): 对折法: 度量法: 教师追问:同学们知道图中三个角的数量关系吗? 学生思考,学生代表回答,师生共同总结与填空. 教师再以此引出角平分线的定义. 定义总结: 师生活动:教师讲解,再让学生朗读定义,加深印象. 类比:仿照角平分线的结论,你能写出角的三等分线的结论吗? 师生活动:学生独立思考,由学生代表发言,教师予以适当评价,帮助学生正确规范完成几何书写. 例3 如图OC是∠AOB的平分线,OB是∠COD的三等平分线,∠BOD = 15°.则∠AOB等于 ( ) A. 75 B. 70 C. 65 D. 60 师生活动:学生独立思考,学生代表发言,教师适时评价与引导. 思考:除此题所给图片的情况,你还能想出其他情况与答案吗? 师生活动:学生独立思考,学生代表上台展示,教师予以评价与指导,得出另一种结果,∠AOB = 15°. 三、当堂练习 1. 比较大小:60°25′ 60.25°(填“>”,“<” 或“=”). 2. 计算: (1) 180° - 98°24′30″ (2) 62°24′17″×4 3. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOB = 50°,∠DOE = 30°,那么∠BOD是多少度? 设计意图:通过建立线段比较长短与角比较大小之间知识与方法的联系,使学生对学习进程心中有数,在对比中加深理解,帮助学生掌握研究问题的方法. 设计意图:采用类比的方法,按照“几何模型--图形--文字--符号”的学习程序,学生动手操作,自主探究. 设计意图:指出对于两个角的大小关系和两个实数的大小关系一样,有且仅有三种情况: ∠AOB <∠A′O′B′, ∠AOB =∠A′O′B′, ∠AOB>∠A′O′B′, 为以后分类研究一些有关角的问题奠定基础. 设计意图:针对同一图形变换审视角度提出问题,可以提高学生的读图能力,用符号表示角的和差关系,仍遵循“几何模型——图形——文字——符号”的学习过程,在图形与等式之间建立一种关系. 设计意图:用一副三角尺画出一些特殊角,除让学生巩固角的和与差概念外,也使学生对这些特殊角的大小有直观的认识,培养对角的大小的估计能力和动手操作能力,加深学生对角的认识. 设计意图:通过题目锻炼学生运算能力,初步学习几何语言在解题中的运用,体会几何与代数之间的联系与不同,加深学生的数形结合思想. 设计意图:从角的和差问题中,将射线OB的位置特殊化,并类比线段的中点,引出角的平分线的概念,不仅知识的产生、发展自然连续,也体现了由一般到特殊,由特殊到一般的研究方法,同时,也能建立知识间的联系,完善认知结构. 设计意图:进一步明晰角平分线的概念,为后续学习轴对称和研究有关图形的翻折问题打下基础. 设计意图:通过类比让学生学会举一反三,体会几何知识的关联性,巩固几何语言的书写. 设计意图:通过题目帮助学生巩固角平分线的知识与角的运算,提高学生的识图能力和运算能力. 又通过思考题启发学生思考其他可能性,建立分类讨论思想,养成严谨思考的习惯. 设计意图:通过练习巩固角的大小比较. 设计意图:通过练习巩固角度的运算. 设计意图:通过练习强化试图能力和运算能力.
板书设计 4.3.2 角的比较与运算 角的概念 角的表示 角的度量和单位
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.
教学反思 数形结合,培养识图能力 角的比较大小、角的和与差、角平分线研究与研究线段的大小比较、和与差、中点的内容和方法很相似,教学时把两者作对比,学生在学习方法和学习内容的理解上,不会有困难.困难在于正确地完成图形语言、文字语言、符号语言之间的转化,究其原因,一方面,语言是思维的产物,图形是实物和模型第一次抽象,是对研究对象的直观反映,文字语言是对图形的描述、理解和讨论,符号语言则是对文字语言的简化和再次抽象.它们的综合运用,要求学生必须对研究对象从数和形上有着深刻的理解,并具有读图和画图的能力;二是需要培养和训练,对于图形、文字、符号语言的综合运用,虽然在学习线段知识时已有接触,但要达到融会贯通的程度还需要经过一段时间的学习和训练.
