柱、锥、台、球的表面积与体积精例(广东)
文档属性
| 名称 | 柱、锥、台、球的表面积与体积精例(广东) |  | |
| 格式 | rar | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-18 23:41:00 | ||
图片预览




文档简介
课件19张PPT。柱、锥、台、球体的
表面积与体积一. 棱柱的侧面积、表面积与体积1. 直棱柱的侧面积、表面积与体积S侧=C?hS表= S侧+2S底2. 斜棱柱的侧面积、表面积与体积S侧=C’?LS表= S侧+2S底二. 棱锥的侧面积、表面积与体积S表= S侧+S底S侧= S△1+S △2 +S △3 +…三. 棱台的侧面积、表面积与体积S表= S侧+S上底+S下底S侧= S梯形1+S梯形2 +S梯形3 +…V棱柱= S?h四. 圆柱的侧面积、表面积与体积S侧=2?rLS表= 2?r(r+L)S表= 4?R2 五. 圆锥的侧面积、表面积与体积S表= ?r(r+L) S侧= ?rL六. 圆台的侧面积、表面积与体积S表=? (r’2+r2+r’ L +r L )
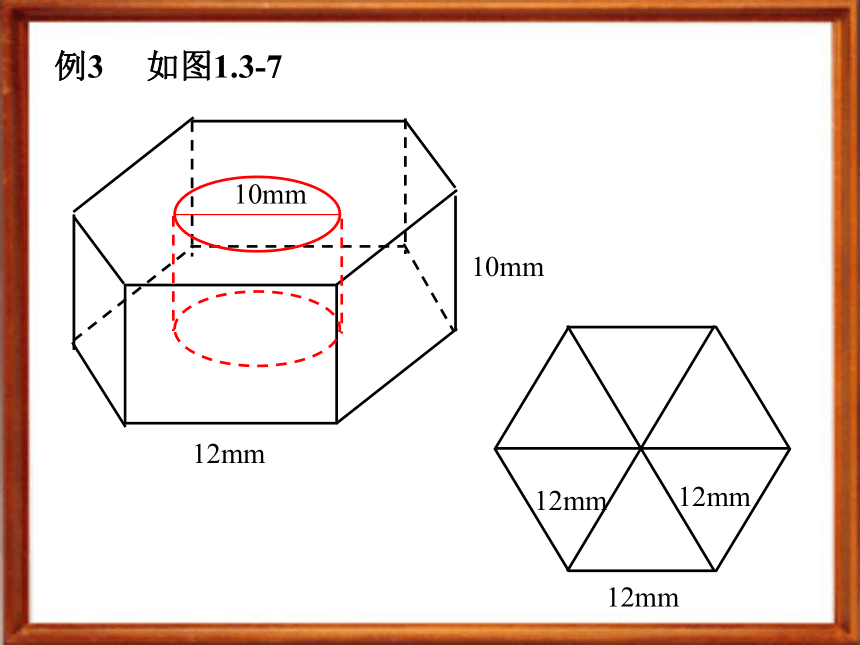
S侧= ? (r’+r) LV圆柱= ?r2h七. 球的表面积与体积典例精析:例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积与体积。D例2 如图1.3-6 例3 如图1.3-712mm10mm10mm12mm12mm12mm例4RRL=2R例1:
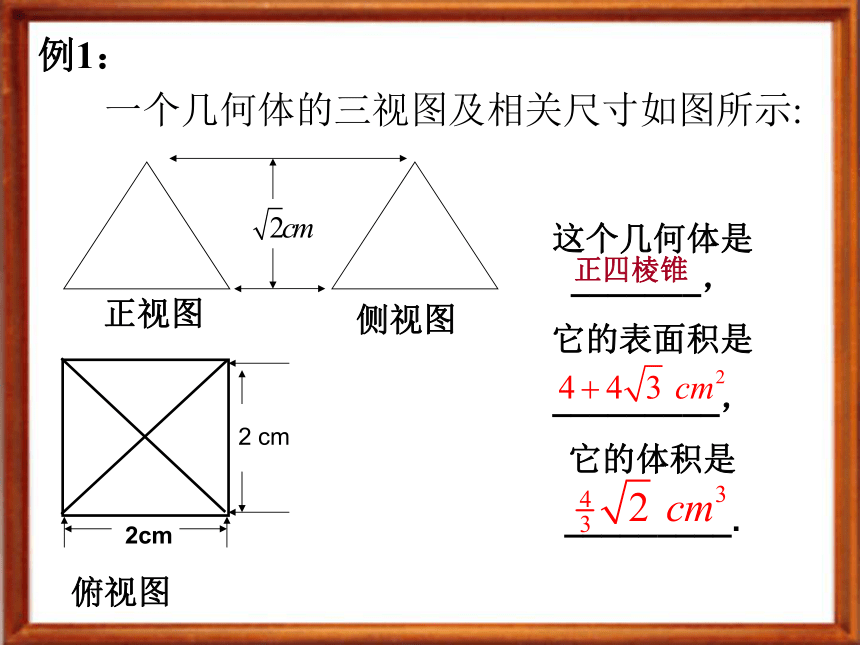
一个几何体的三视图及相关尺寸如图所示:俯视图
这个几何体是_______,
它的表面积是
_________,
它的体积是
_________.正视图侧视图 2 cm2cm正四棱锥变式1:一几何体的三视图及相关尺寸如图所示:俯视图这个几何体是
____ ___,
它的表面积是
_________,
它的体积是
_________.正视图侧视图 2 cm2cm由正四棱锥和长方体组合而成 1 cm例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。32A1BCDA1D1C1B112例2
已知长方体ABCD-A1B1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。32A1aBCDA1D1C1B121例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。 32A1BCDA1D1C1B1变式2
已知正方体的棱长为a,有一只蚂蚁从点A出发经正方体的侧面走一周到达点A1,求蚂蚁走的最短距离。例3 在底面边长为a,侧棱长为2a的正四棱柱ABCD-A1B1C1D1中,求:此棱柱的体积V;
点B到平面AB1C的距离。VB-AB1C= VB1-ABC
= VA-BB1C
= VC-ABB1 变式3
已知正三棱锥S-ABC的侧棱两两垂直,侧棱长为 ,求:此棱锥的体积V;
点S到底面ABC的距离。VS-ABC= VB-SAC
= VA-SBC
= VC-SABSABC例4:
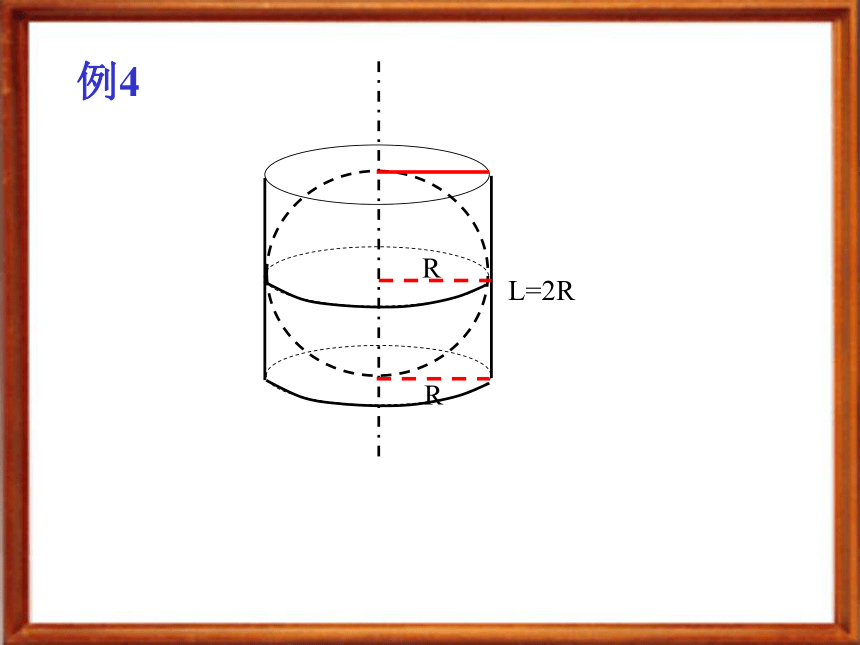
设正方体的表面积为24cm2,一个球内切于该正方体,另一球外接于该正方体,求两球的体积。Ra=2R例4Ra=2RL=2R
L2=3a2例5:
在Rt△ABC中,AC=3,BC=4,AB=5,求分别以三角形的三边为旋转轴旋转一周所成的旋转体的表面积与体积。543543354ABCBACCAB思考:2.一个正方体和一个圆柱等高,并且侧面积相等。比较它们的体积哪个大?为什么?3.求证:经过长方体相对两个面的中心的任意平面,把长方体分成体积相等的两个柱体。1.用棱长为1的正方体的体积作为单位体积,下图长方体的体积的数值为24.假如将体积单位改用棱长为2的正方体的体积,这个长方体的体积变为多少?
表面积与体积一. 棱柱的侧面积、表面积与体积1. 直棱柱的侧面积、表面积与体积S侧=C?hS表= S侧+2S底2. 斜棱柱的侧面积、表面积与体积S侧=C’?LS表= S侧+2S底二. 棱锥的侧面积、表面积与体积S表= S侧+S底S侧= S△1+S △2 +S △3 +…三. 棱台的侧面积、表面积与体积S表= S侧+S上底+S下底S侧= S梯形1+S梯形2 +S梯形3 +…V棱柱= S?h四. 圆柱的侧面积、表面积与体积S侧=2?rLS表= 2?r(r+L)S表= 4?R2 五. 圆锥的侧面积、表面积与体积S表= ?r(r+L) S侧= ?rL六. 圆台的侧面积、表面积与体积S表=? (r’2+r2+r’ L +r L )
S侧= ? (r’+r) LV圆柱= ?r2h七. 球的表面积与体积典例精析:例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积与体积。D例2 如图1.3-6 例3 如图1.3-712mm10mm10mm12mm12mm12mm例4RRL=2R例1:
一个几何体的三视图及相关尺寸如图所示:俯视图
这个几何体是_______,
它的表面积是
_________,
它的体积是
_________.正视图侧视图 2 cm2cm正四棱锥变式1:一几何体的三视图及相关尺寸如图所示:俯视图这个几何体是
____ ___,
它的表面积是
_________,
它的体积是
_________.正视图侧视图 2 cm2cm由正四棱锥和长方体组合而成 1 cm例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。32A1BCDA1D1C1B112例2
已知长方体ABCD-A1B1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。32A1aBCDA1D1C1B121例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,求沿其表面从点A到点C1的最短距离。 32A1BCDA1D1C1B1变式2
已知正方体的棱长为a,有一只蚂蚁从点A出发经正方体的侧面走一周到达点A1,求蚂蚁走的最短距离。例3 在底面边长为a,侧棱长为2a的正四棱柱ABCD-A1B1C1D1中,求:此棱柱的体积V;
点B到平面AB1C的距离。VB-AB1C= VB1-ABC
= VA-BB1C
= VC-ABB1 变式3
已知正三棱锥S-ABC的侧棱两两垂直,侧棱长为 ,求:此棱锥的体积V;
点S到底面ABC的距离。VS-ABC= VB-SAC
= VA-SBC
= VC-SABSABC例4:
设正方体的表面积为24cm2,一个球内切于该正方体,另一球外接于该正方体,求两球的体积。Ra=2R例4Ra=2RL=2R
L2=3a2例5:
在Rt△ABC中,AC=3,BC=4,AB=5,求分别以三角形的三边为旋转轴旋转一周所成的旋转体的表面积与体积。543543354ABCBACCAB思考:2.一个正方体和一个圆柱等高,并且侧面积相等。比较它们的体积哪个大?为什么?3.求证:经过长方体相对两个面的中心的任意平面,把长方体分成体积相等的两个柱体。1.用棱长为1的正方体的体积作为单位体积,下图长方体的体积的数值为24.假如将体积单位改用棱长为2的正方体的体积,这个长方体的体积变为多少?
