2.4 二次函数的应用——最大面积是多少 教学设计(表格式) 北师大版数学九年级下册
文档属性
| 名称 | 2.4 二次函数的应用——最大面积是多少 教学设计(表格式) 北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 30.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 09:43:26 | ||
图片预览

文档简介
数学九年级下北师大版
2.4节《二次函数的应用(1)》教学设计
一、教学目标
知识与技能:
能够分析和表示实际问题中变量之间的二次函数关系,并且能够运用二次函数的知识解决实际问题中的最大(小)值,增强解决问题的能力。
过程与方法:
通过分析和表示实际问题中变量之间的二次函数关系,经历求最大面积问题的探索过程,提高学生用数学知识解决实际问题的能力,培养学生的数学应用能力。
情感态度与价值观:
1.经历探究矩形最大面积问题的过程,获得利用数学方法解决实际问题的经验,并进一步感受数学模型思想和数学的应用价值.
2.在独立思考问题的基础上,敢于发表自己的观点,从交流讨论中获得成功的体验,增进学生对数学的理解和学好数学的信心。
二、 教学重点
能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题中的最大(小)值.
三、 教学难点
把实际问题转化成“二次函数”模型,从而解决问题
课程类型
新授课
教学方法
分组交流讨论法、自主探究法.
六、 教学工具
多媒体课件
教学过程
教师活动 学生活动 设计意图
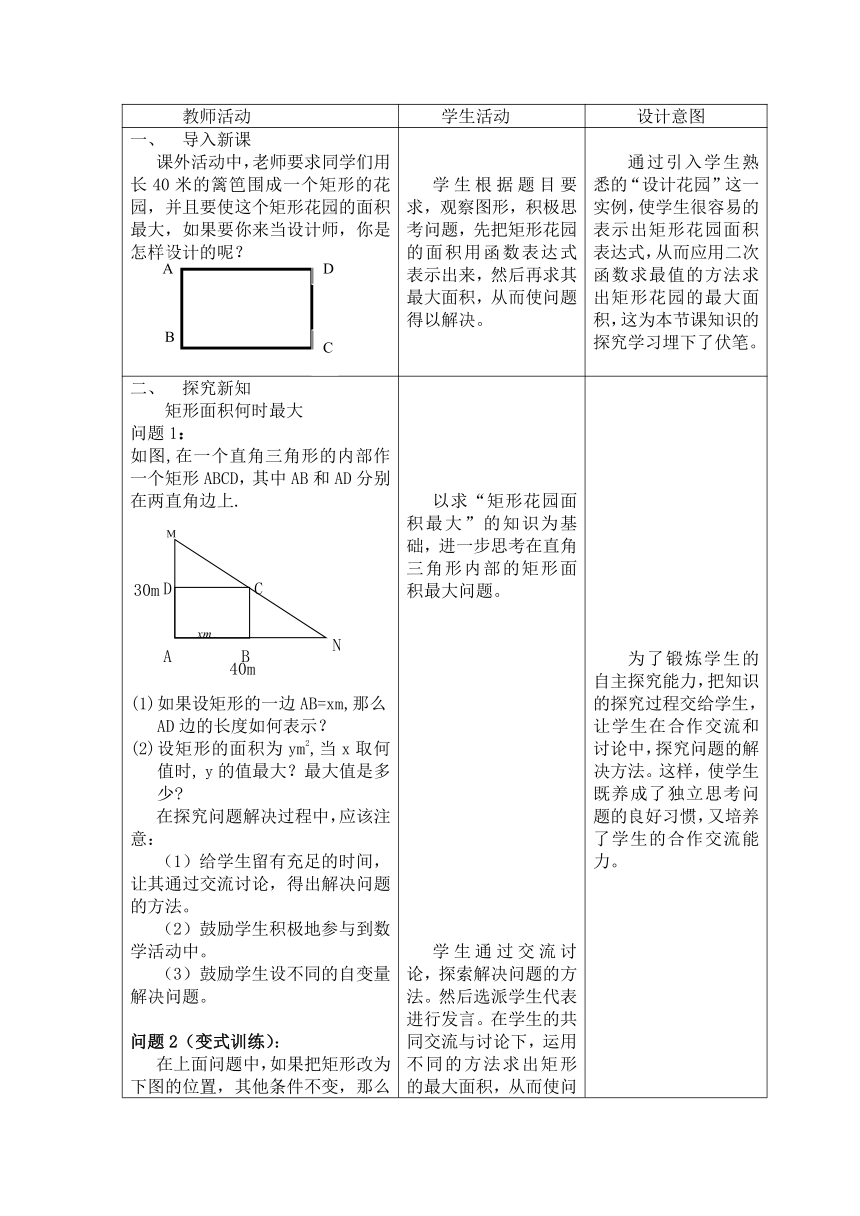
导入新课 课外活动中,老师要求同学们用长40米的篱笆围成一个矩形的花园,并且要使这个矩形花园的面积最大,如果要你来当设计师,你是怎样设计的呢? (
A
D
B
C
) 学生根据题目要求,观察图形,积极思考问题,先把矩形花园的面积用函数表达式表示出来,然后再求其最大面积,从而使问题得以解决。 通过引入学生熟悉的“设计花园”这一实例,使学生很容易的表示出矩形花园面积表达式,从而应用二次函数求最值的方法求出矩形花园的最大面积,这为本节课知识的探究学习埋下了伏笔。
探究新知 矩形面积何时最大 问题1: 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上. (
N
) (
D
B
A
C
M
4
0
m
30
m
m
m
) 如果设矩形的一边AB=xm,那么AD边的长度如何表示? 设矩形的面积为ym2,当x取何值时, y的值最大?最大值是多少 在探究问题解决过程中,应该注意: (1)给学生留有充足的时间,让其通过交流讨论,得出解决问题的方法。 (2)鼓励学生积极地参与到数学活动中。 (3)鼓励学生设不同的自变量解决问题。 问题2(变式训练): 在上面问题中,如果把矩形改为下图的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样解决这个问题的? (
D
A
B
C
M
P
N
) 在此问题的解决过程中,教师同样要给学生留有充分的时间进行探究,如果学生探究问题的解决方法时有困难,那么就要引导学生进行问题的思考与解决。 。 以求“矩形花园面积最大”的知识为基础,进一步思考在直角三角形内部的矩形面积最大问题。 学生通过交流讨论,探索解决问题的方法。然后选派学生代表进行发言。在学生的共同交流与讨论下,运用不同的方法求出矩形的最大面积,从而使问题得以解决。 学生以前面问题的探究经验为基础,探究变化后的图形和前面图形的区别与联系,类比前一问题的解决方法,解决此问题。然后请学生代表发言,其他学生给与补充和指正。 为了锻炼学生的自主探究能力,把知识的探究过程交给学生,让学生在合作交流和讨论中,探究问题的解决方法。这样,使学生既养成了独立思考问题的良好习惯,又培养了学生的合作交流能力。 经过观察、思考、类比等数学活动,培养学生解决问题的能力,让学生在问题的解决中体会知识的应用方法,使学生获得成功的体验。
归纳总结 请同学们根据解决“矩形面积最大问题”的经验,尝试总结解决此类问题的基本思路是什么? 根据自己解决问题的经验和见解,总结解决此类问题的基本思路。 培养学生的总结归纳能力和语言表达能力。
四、巩固新知 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多 (结果精确到0.01m) 此时,窗户的面积是多少 (结果精确到0.01m) (
x
x
y
) 在“最大面积”问题的解决基础上再次引导学生探究“何时窗户通过的光线最多”问题,使学生能够清楚地认识到这两类问题的关系 鼓励学生根据前面知识的经验,独立思考并探究问题的解决方法,完成解题过程的书写。 使学生进一步巩固所学知识,达到学以致用的目的,提高学生的知识应用能力。
课堂小结 谈谈你本节课的收获 学生畅所欲言,谈自己本节课的收获。 锻炼学生的语言组织和叙述能力。
作业布置: 习题2.8 2、3、4题
八、板书设计
二次函数的应用 ——最大面积是多少 一、情景引入 三、课堂小结 二、探究新知 四、作业布置 矩形最大面积问题 “变式训练” 解决面积最大问题的基本思路
2.4节《二次函数的应用(1)》教学设计
一、教学目标
知识与技能:
能够分析和表示实际问题中变量之间的二次函数关系,并且能够运用二次函数的知识解决实际问题中的最大(小)值,增强解决问题的能力。
过程与方法:
通过分析和表示实际问题中变量之间的二次函数关系,经历求最大面积问题的探索过程,提高学生用数学知识解决实际问题的能力,培养学生的数学应用能力。
情感态度与价值观:
1.经历探究矩形最大面积问题的过程,获得利用数学方法解决实际问题的经验,并进一步感受数学模型思想和数学的应用价值.
2.在独立思考问题的基础上,敢于发表自己的观点,从交流讨论中获得成功的体验,增进学生对数学的理解和学好数学的信心。
二、 教学重点
能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题中的最大(小)值.
三、 教学难点
把实际问题转化成“二次函数”模型,从而解决问题
课程类型
新授课
教学方法
分组交流讨论法、自主探究法.
六、 教学工具
多媒体课件
教学过程
教师活动 学生活动 设计意图
导入新课 课外活动中,老师要求同学们用长40米的篱笆围成一个矩形的花园,并且要使这个矩形花园的面积最大,如果要你来当设计师,你是怎样设计的呢? (
A
D
B
C
) 学生根据题目要求,观察图形,积极思考问题,先把矩形花园的面积用函数表达式表示出来,然后再求其最大面积,从而使问题得以解决。 通过引入学生熟悉的“设计花园”这一实例,使学生很容易的表示出矩形花园面积表达式,从而应用二次函数求最值的方法求出矩形花园的最大面积,这为本节课知识的探究学习埋下了伏笔。
探究新知 矩形面积何时最大 问题1: 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上. (
N
) (
D
B
A
C
M
4
0
m
30
m
m
m
) 如果设矩形的一边AB=xm,那么AD边的长度如何表示? 设矩形的面积为ym2,当x取何值时, y的值最大?最大值是多少 在探究问题解决过程中,应该注意: (1)给学生留有充足的时间,让其通过交流讨论,得出解决问题的方法。 (2)鼓励学生积极地参与到数学活动中。 (3)鼓励学生设不同的自变量解决问题。 问题2(变式训练): 在上面问题中,如果把矩形改为下图的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样解决这个问题的? (
D
A
B
C
M
P
N
) 在此问题的解决过程中,教师同样要给学生留有充分的时间进行探究,如果学生探究问题的解决方法时有困难,那么就要引导学生进行问题的思考与解决。 。 以求“矩形花园面积最大”的知识为基础,进一步思考在直角三角形内部的矩形面积最大问题。 学生通过交流讨论,探索解决问题的方法。然后选派学生代表进行发言。在学生的共同交流与讨论下,运用不同的方法求出矩形的最大面积,从而使问题得以解决。 学生以前面问题的探究经验为基础,探究变化后的图形和前面图形的区别与联系,类比前一问题的解决方法,解决此问题。然后请学生代表发言,其他学生给与补充和指正。 为了锻炼学生的自主探究能力,把知识的探究过程交给学生,让学生在合作交流和讨论中,探究问题的解决方法。这样,使学生既养成了独立思考问题的良好习惯,又培养了学生的合作交流能力。 经过观察、思考、类比等数学活动,培养学生解决问题的能力,让学生在问题的解决中体会知识的应用方法,使学生获得成功的体验。
归纳总结 请同学们根据解决“矩形面积最大问题”的经验,尝试总结解决此类问题的基本思路是什么? 根据自己解决问题的经验和见解,总结解决此类问题的基本思路。 培养学生的总结归纳能力和语言表达能力。
四、巩固新知 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多 (结果精确到0.01m) 此时,窗户的面积是多少 (结果精确到0.01m) (
x
x
y
) 在“最大面积”问题的解决基础上再次引导学生探究“何时窗户通过的光线最多”问题,使学生能够清楚地认识到这两类问题的关系 鼓励学生根据前面知识的经验,独立思考并探究问题的解决方法,完成解题过程的书写。 使学生进一步巩固所学知识,达到学以致用的目的,提高学生的知识应用能力。
课堂小结 谈谈你本节课的收获 学生畅所欲言,谈自己本节课的收获。 锻炼学生的语言组织和叙述能力。
作业布置: 习题2.8 2、3、4题
八、板书设计
二次函数的应用 ——最大面积是多少 一、情景引入 三、课堂小结 二、探究新知 四、作业布置 矩形最大面积问题 “变式训练” 解决面积最大问题的基本思路
