青岛版数学八年级上册 2.4线段的垂直平分线第1课时 (共20张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.4线段的垂直平分线第1课时 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
2.4 线段的垂直平分线
第1课时 线段的垂直平分线的性质与判定
学习目标
1.经历线段的轴对称性质的探索过程,理解线段的垂直平分线的概念;
2.探索线段的垂直平分线的性质;
3.能用尺规作一条线段的垂直平分线.
复习回顾
A
B
C
A′
C′
B′
P
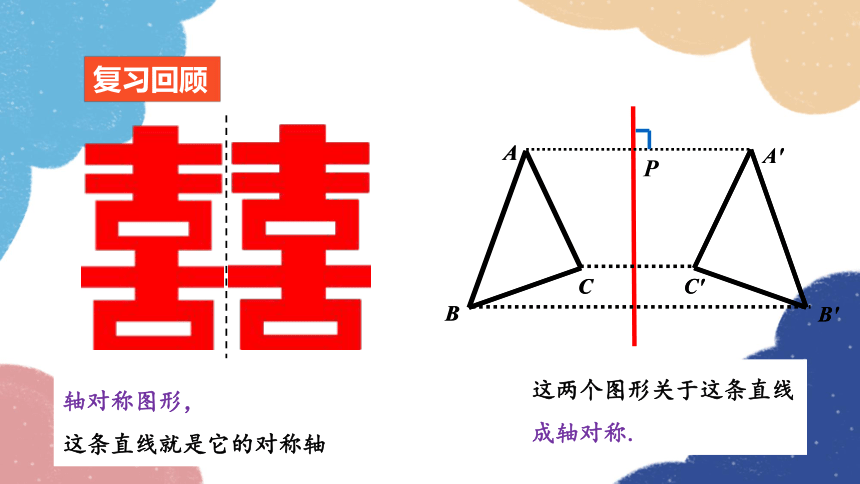
轴对称图形,
这条直线就是它的对称轴
这两个图形关于这条直线
成轴对称.
A
B
C
A′
C′
B′
情境引入
市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等?
B
合作探究
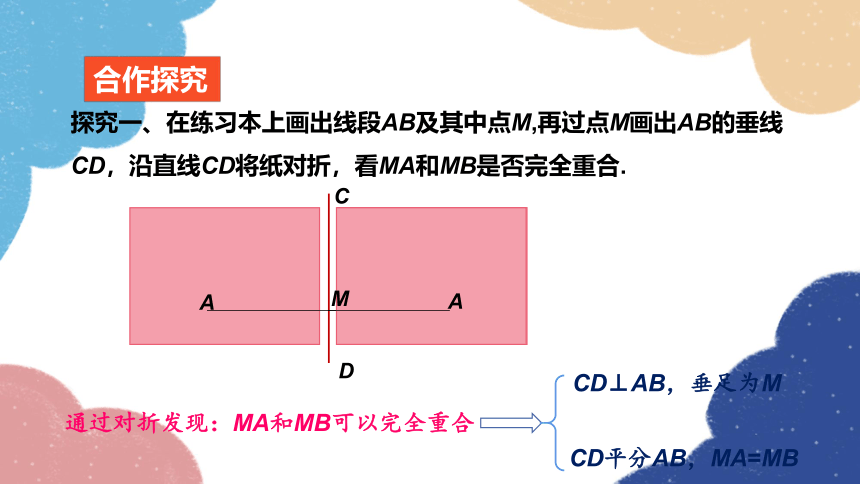
探究一、在练习本上画出线段AB及其中点M,再过点M画出AB的垂线CD,沿直线CD将纸对折,看MA和MB是否完全重合.
通过对折发现:MA和MB可以完全重合
CD⊥AB,垂足为M
CD平分AB,MA=MB
A
C
D
A
M
B
合作探究
通过对折发现:MA和MB可以完全重合
CD⊥AB,垂足为M
CD平分AB,MA=MB
A
C
D
A
M
垂直并且平分一条线段的直线叫做这条线段的垂直平分线.
直线CD即是线段AB的垂直平分线,同时还是线段AB的一条对称轴.
合作探究
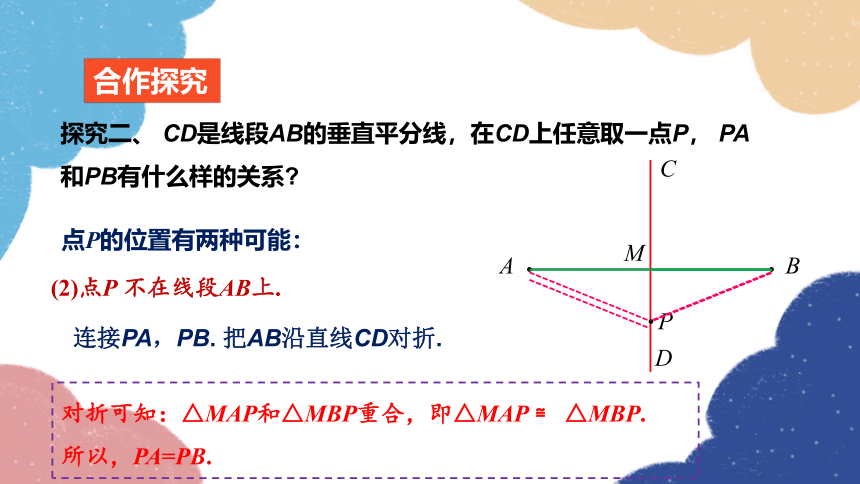
探究二、 CD是线段AB的垂直平分线,在CD上任意取一点P, PA和PB有什么样的关系
A
C
D
B
M
(P)
点P的位置有两种可能:
(1)点P 恰是CD和线段AB的交点.
此时点P与点M重合,所以PA=PB.
合作探究
探究二、 CD是线段AB的垂直平分线,在CD上任意取一点P, PA和PB有什么样的关系
A
C
D
B
M
连接PA,PB. 把AB沿直线CD对折.
P
对折可知:△MAP和△MBP重合,即△MAP ≌ △MBP.
所以,PA=PB.
点P的位置有两种可能:
(2)点P 不在线段AB上.
线段垂直平分线的性质
二
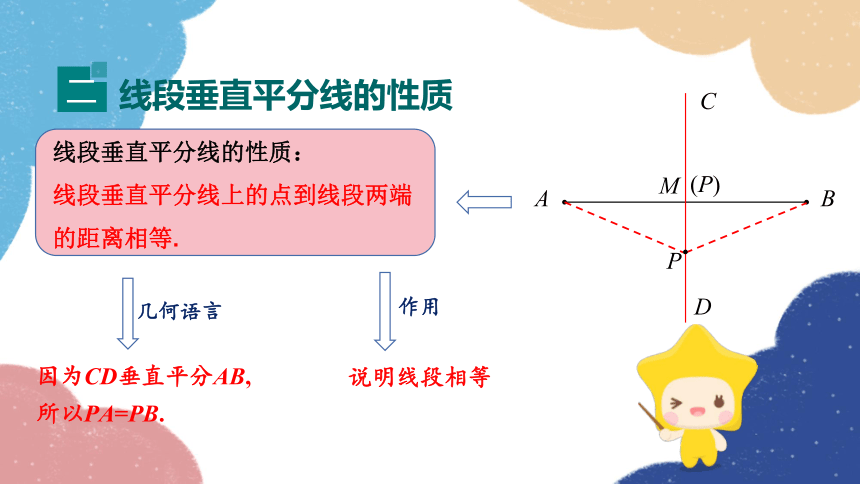
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
A
C
D
B
M
P
(P)
几何语言
因为CD垂直平分AB,
所以PA=PB.
作用
说明线段相等
合作探究
探究三、如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
A
C
D
B
(1)点P 在线段AB上.
点P是AB的中点,
此时点P在线段AB的垂直平分线上.
P
点P的位置有两种可能:
合作探究
(2)点P 在线段AB外.
A
B
P
M
设线段AB的中点为M,则MA=MB.
连接PM,由SSS可知△PMA≌△PMB.
因为∠PMA+∠PMB=180°,
所以∠PMA=90°,即PM⊥AB.
所以点P在线段AB的垂直平分线上.
探究三、如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P的位置有两种可能:
C
D
线段垂直平分线的判定
三
A
C
D
B
M
P
(P)
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
几何语言
作用
因为PA=PB,
所以点P在线段AB的垂直平分线上.
说明点在直线上
合作探究
探究四、如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端距离相等的两点并连接即可.
已知:线段AB.
求作:线段AB的垂直平分线.
合作探究
A
B
(2)过C,D两点作直线CD. CD即为所求.
C
D
合作交流,折纸检验所作直线是否是线段AB的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
合作探究
A
B
C
D
随堂练习
1.如图,已知AB是线段CD的垂直
平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;
如果∠ECD=60°,那么
∠EDC=______.
E
D
A
B
C
7
60°
2.如图所示,在△ABC中,AD垂直平分BC,AC=EC,点B,D,
C,E在同一条直线上,则AB+DB与DE之间的数量关系是( )
A. AB+DB>DE B. AB+DB随堂练习
【解析】因为AD垂直平分BC,所以 AB=AC,BD=CD,
因为AC=EC,所以AB+DB=AC+DC=EC+DC=DE .
C
3.已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是 ( )
A.24 cm和12 cm B.16 cm和22 cm
C.20 cm和16 cm D.22 cm和16 cm
随堂练习
【解析】AB的垂直平分线与边AC交于D,则BD=AD,
故BD+DC=AC,所以AB=60-38=22(cm),AC=22 (cm),
BC=38-22=16(cm).
D
4.已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
说明:PA=PB=PC.
B
A
C
M
N
M′
N′
P
解:因为MN垂直平分AB,
所以PA=PB.
同理 PB=PC.
所以PA=PB=PC.
随堂练习
三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等.
课堂小结
点在线段的垂直平分线上
性质
点到线段两端距离相等
判定
条件
结论
条件
结论
线段垂直平分线的性质与判定之间的关系
2.4 线段的垂直平分线
第1课时 线段的垂直平分线的性质与判定
学习目标
1.经历线段的轴对称性质的探索过程,理解线段的垂直平分线的概念;
2.探索线段的垂直平分线的性质;
3.能用尺规作一条线段的垂直平分线.
复习回顾
A
B
C
A′
C′
B′
P
轴对称图形,
这条直线就是它的对称轴
这两个图形关于这条直线
成轴对称.
A
B
C
A′
C′
B′
情境引入
市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等?
B
合作探究
探究一、在练习本上画出线段AB及其中点M,再过点M画出AB的垂线CD,沿直线CD将纸对折,看MA和MB是否完全重合.
通过对折发现:MA和MB可以完全重合
CD⊥AB,垂足为M
CD平分AB,MA=MB
A
C
D
A
M
B
合作探究
通过对折发现:MA和MB可以完全重合
CD⊥AB,垂足为M
CD平分AB,MA=MB
A
C
D
A
M
垂直并且平分一条线段的直线叫做这条线段的垂直平分线.
直线CD即是线段AB的垂直平分线,同时还是线段AB的一条对称轴.
合作探究
探究二、 CD是线段AB的垂直平分线,在CD上任意取一点P, PA和PB有什么样的关系
A
C
D
B
M
(P)
点P的位置有两种可能:
(1)点P 恰是CD和线段AB的交点.
此时点P与点M重合,所以PA=PB.
合作探究
探究二、 CD是线段AB的垂直平分线,在CD上任意取一点P, PA和PB有什么样的关系
A
C
D
B
M
连接PA,PB. 把AB沿直线CD对折.
P
对折可知:△MAP和△MBP重合,即△MAP ≌ △MBP.
所以,PA=PB.
点P的位置有两种可能:
(2)点P 不在线段AB上.
线段垂直平分线的性质
二
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
A
C
D
B
M
P
(P)
几何语言
因为CD垂直平分AB,
所以PA=PB.
作用
说明线段相等
合作探究
探究三、如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
A
C
D
B
(1)点P 在线段AB上.
点P是AB的中点,
此时点P在线段AB的垂直平分线上.
P
点P的位置有两种可能:
合作探究
(2)点P 在线段AB外.
A
B
P
M
设线段AB的中点为M,则MA=MB.
连接PM,由SSS可知△PMA≌△PMB.
因为∠PMA+∠PMB=180°,
所以∠PMA=90°,即PM⊥AB.
所以点P在线段AB的垂直平分线上.
探究三、如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P的位置有两种可能:
C
D
线段垂直平分线的判定
三
A
C
D
B
M
P
(P)
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
几何语言
作用
因为PA=PB,
所以点P在线段AB的垂直平分线上.
说明点在直线上
合作探究
探究四、如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端距离相等的两点并连接即可.
已知:线段AB.
求作:线段AB的垂直平分线.
合作探究
A
B
(2)过C,D两点作直线CD. CD即为所求.
C
D
合作交流,折纸检验所作直线是否是线段AB的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
合作探究
A
B
C
D
随堂练习
1.如图,已知AB是线段CD的垂直
平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;
如果∠ECD=60°,那么
∠EDC=______.
E
D
A
B
C
7
60°
2.如图所示,在△ABC中,AD垂直平分BC,AC=EC,点B,D,
C,E在同一条直线上,则AB+DB与DE之间的数量关系是( )
A. AB+DB>DE B. AB+DB
【解析】因为AD垂直平分BC,所以 AB=AC,BD=CD,
因为AC=EC,所以AB+DB=AC+DC=EC+DC=DE .
C
3.已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是 ( )
A.24 cm和12 cm B.16 cm和22 cm
C.20 cm和16 cm D.22 cm和16 cm
随堂练习
【解析】AB的垂直平分线与边AC交于D,则BD=AD,
故BD+DC=AC,所以AB=60-38=22(cm),AC=22 (cm),
BC=38-22=16(cm).
D
4.已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
说明:PA=PB=PC.
B
A
C
M
N
M′
N′
P
解:因为MN垂直平分AB,
所以PA=PB.
同理 PB=PC.
所以PA=PB=PC.
随堂练习
三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等.
课堂小结
点在线段的垂直平分线上
性质
点到线段两端距离相等
判定
条件
结论
条件
结论
线段垂直平分线的性质与判定之间的关系
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
