八年级上期中测试数学冀教版2

八年级上册第一学期期中水平测试题（B）
一、选择题：（每小题3分，共30分）
1. “—x不大于—2”用不等式表示为（ ）．
A．—x≥—2 B．—x ≤—2 C．—x ＞—2 D．—x ＜—2
2. 不等式组的最大整数解是（ ）．
A．x =－2 B．x =2 C．x =3 D．x =4
3. 若x、y的值均扩大为原来的2倍，则下列分式的值保持不变的是（ ）
A． B． C． D．
4. 若，则得值为（ ）
A． B. C. D.2
5. 一个圆桶底面直径为24cm，高32cm，则桶内所能容下的最长木棒为（ ）
A．20cm B．50cm C．40cm D．45cm
6. 如图6，四个全等直角三角形与中间的小正方形拼成一个大正方形，如果大正方形的面积是13，小正方形的面积是1，且直角三角形中，短直角边长为a，长直角边长为b，则的值为（ ）
A． 13 B．19 C．25 D．169
7. 下列说法中正确的有（ ）个
①如果∠A＋∠B=∠C，那么△ABC是直角三角形．
②如果∠A∶∠B∶∠C=5∶4∶3，则△ABC是直角三角形．
③如果三角形的三边分别为3k∶4k∶5k（k>0），则△ABC是直角三角形．
④如果三边长分别为，，（n>1），则△ABC是直角三角形．
A. 1个 B. 2个 C. 3个 D.4个
8. 一种灭虫药30㎏含药率15%，现在用含药率较高的同种灭虫药50㎏和它混合，使混合后的含药率大于20%，且小于35%，则所用药粉的含药率x的取值范围是（ ）
A. 15%9. 下列图案是几种名车的标志，是轴对称图形的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图10，∠B与∠C的平分线相交于点O，过点O作MN∥BC，其AB=12，AC=18，BC=24，则△AMN周长为（ ）
A. 30 B. 36 C. 39 D.42
二、填空题：（3×10=30分）
11. 不等式－2x＜1的解集是 ．
12. 代数式的值小于5 且大于0，则x的取值范围是 ．
13. x___________时，分式的值为0．
14. 在电路中两电子元件以并联连接，已知这时的总电阻R=4欧，一电子元件电阻为=6欧，则另一电元的阻值为　　　　欧． （）
15. 小强站在镜子前，镜子中映出他运动服的号码如图所示，你知道小强衣服上的号码是_____________．
16. 一个直角三角形的三边长是不大于10的三个连续偶数，则它的周长是
17. 一座桥长12米，一艘小船自桥北头出发，向正南方向驶去，因水流原因，到达南岸后，发现已偏离桥南头9米，则小船实际行驶了____________米．
18. 若等腰三角形的底角为15°，腰长为2，则腰上的高为
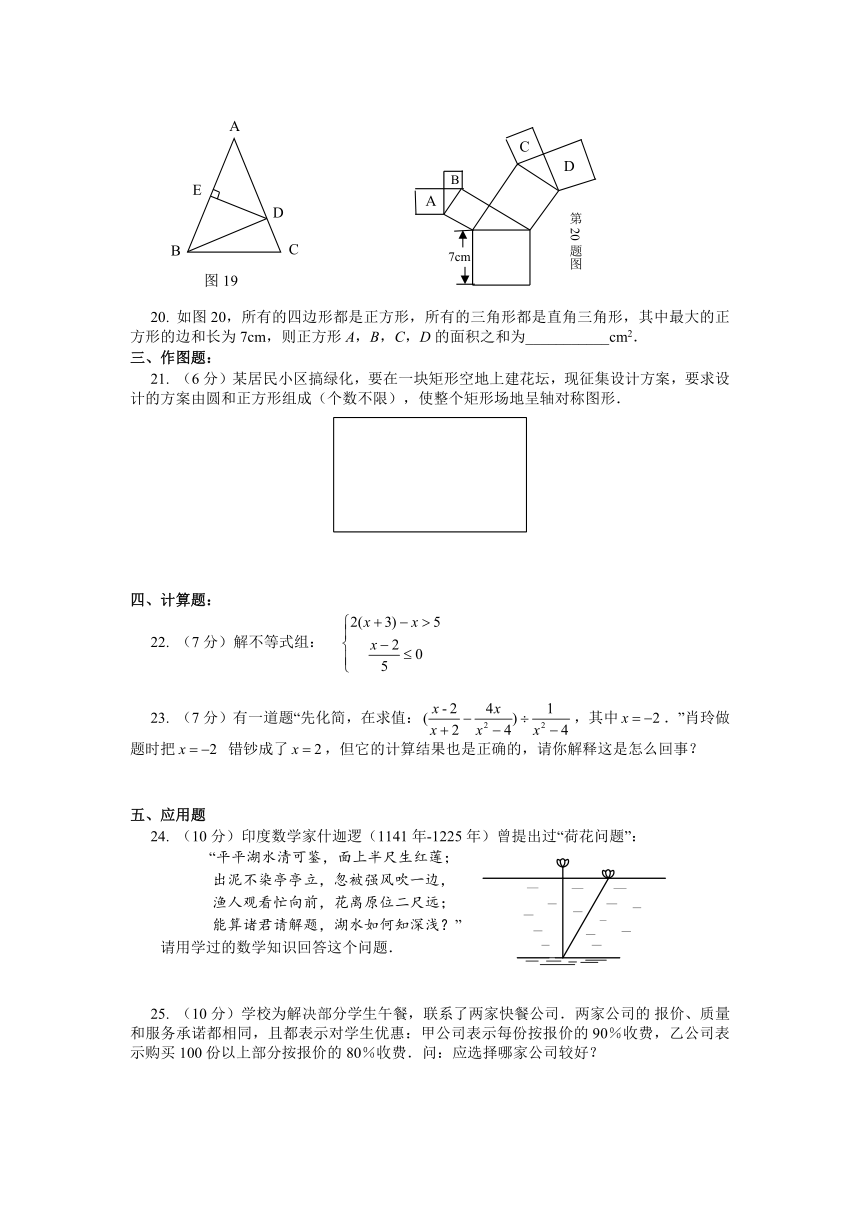
19. 如图19，△ABC中，AB=AC，DE垂直平分AB，△BDC周长是8，且AC－BC=2，则AB=____．
20. 如图20，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm，则正方形A，B，C，D的面积之和为___________cm2．
三、作图题：
21. （6分）某居民小区搞绿化，要在一块矩形空地上建花坛，现征集设计方案，要求设计的方案由圆和正方形组成（个数不限），使整个矩形场地呈轴对称图形．
四、计算题：
22. （7分）解不等式组：
23. （7分）有一道题“先化简，在求值：，其中．”肖玲做题时把 错钞成了，但它的计算结果也是正确的，请你解释这是怎么回事？
五、应用题
24. （10分）印度数学家什迦逻（1141年-1225年）曾提出过“荷花问题”：
“平平湖水清可鉴，面上半尺生红莲；
出泥不染亭亭立，忽被强风吹一边，
渔人观看忙向前，花离原位二尺远；
能算诸君请解题，湖水如何知深浅？”
请用学过的数学知识回答这个问题．
25. （10分）学校为解决部分学生午餐，联系了两家快餐公司．两家公司的 报价、质量和服务承诺都相同，且都表示对学生优惠：甲公司表示每份按报价的90％收费，乙公司表示购买100份以上部分按报价的80％收费．问：应选择哪家公司较好？
26. 如图26，在Rt△ABC中，AB=AC，∠BAC=90°，点O为BC的中点，在AB、AC上有两个动点M和N，在移动中保持AN=BM，请猜想△OMN的形状，并证明你的猜想．
六、探究天地：
27. （10分）小阳暑假到姑姑家去玩，吃早点时，表妹佳佳很淘气，她先从一杯豆浆中取出一勺豆浆，倒入盛牛奶的杯子中搅匀，再从盛牛奶的杯子中取出一勺混合的牛奶和豆浆，放入盛豆浆的杯子中．小阳想，现在两个杯子中都有了牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A C C C C C C A
二、填空题
题号 11 12 13 14 15
答案 3 12 610537
题号 16 17 18 19 20
答案 24 15 1 13 49
三、作图题
略
四、计算题
22.
解不等式（1）得：
解不等式（2）得：
所以不等式组的解：
23.解：
=
=
当时，原式==8
当时，原式==8
所以肖玲做题时把 错钞成了，但它的计算结果也是正确的．
五、应用
24.
解：如图，由题意可知：∠ADC=∠BDC=90°；红莲高出水面AD=1尺；花朵齐及水面说明：AB=BC；红莲移动的水平距离为2尺说明：DC=2尺．
设水深BD=x尺，则AB=BC=(x+1) 尺
在Rt△BDC中，根据勾股定理得：
所以
解得：
答：这里水深是1.5尺
25. 解：设每份午餐a元，学校需购买x份午餐，根据题意得：
甲公司应收费：90％ax
乙公司应收费：100a＋80％a（x－100）
（1）∵90％ax=100a＋80％a（x－100）
90％x=100＋80％（x－100）
0.9x=100＋0.8x－80
0.1x=20
X=200
∴当购买200份时，两家公司的总费用相同，那家公司都可以．
（2）∵90％ax>100a＋80％a（x－100）
∴x>200
∴当购买200份以上时，乙公司的总费用低，选择乙公司较好．
（3）∵90％ax<100a＋80％a（x－100）
∴x<200
∴当购买200份以下时，甲公司的总费用低，选择甲公司较好．
26.如图26，在Rt△ABC中，AB=AC，∠BAC=90°，点O为BC的中点，在AB、AC上有两个动点M和N，在移动中保持AN=BM，请猜想△OMN的形状，并证明你的猜想．
答：△OMN是等腰直角三角形．
理由：如右图，连结OA
∵AB=AC，∠BAC=90°；OB=OC
∴∠B=∠C=∠OAN=45°；AO⊥BC
∴OA=OB=OC
在△OAN和△OBM中
∴△OAN≌△OBM（SAS）
∴ON=OM；∠AON=∠BOM
∵AO⊥BC
∴∠AOB=90°
∴∠MON=∠AON＋∠AOM=∠BOM＋∠AOM=∠AOB=90°
∴△OMN是等腰直角三角形．
六、探究天地
27. 小阳暑假到姑姑家去玩，吃早点时，表妹佳佳很淘气，她先从一杯豆浆中取出一勺豆浆，倒入盛牛奶的杯子中搅匀，再从盛牛奶的杯子中取出一勺混合的牛奶和豆浆，放入盛豆浆的杯子中．小阳想，现在两个杯子中都有了牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？
解：假设混合前两个杯子中盛的牛奶和豆浆的体积相等，均为a，勺的体积为b，混合前后的数量关系列成下面的表格．
　 混合前的体积 第一次混合后的体积 第二次混合后的体积
　 豆浆 牛奶 豆浆 牛奶 豆浆 牛奶
豆浆杯子 a 0 0
牛奶杯子 0 a b a
最后豆浆杯子中的牛奶为，牛奶杯子中的豆浆为
因为：==0
所以=
即：豆浆杯子中的牛奶与牛奶杯子中的豆浆一样多．
B
A
N
M
C
O
图10
A
B
C
E
D
图19
C
B
A
A
N
B
O
7cm
第20题图
D
C
B
A
图26
M
C
A
N
D
N
B
O
图26
M
C
B
O
A
C
M
图26