5.6二次函数的图像与一元二次方程课件
图片预览






文档简介
课件24张PPT。5.6二次函数的图像与一元二次方程中国历史上的方程求解 约公元50~100年编成的《九章算术》,以算法形式给出了求一次方程、二次方程和正系数三次方程根的方法。
7世纪,隋唐数学家王孝通找出了求三次方程正根的数值解法。
11世纪北宋数学家贾宪以“立成释锁法”解三次或三次以上的高次方程式,同时,还提出了一种更简单的“增乘开方法”。
13世纪,南宋数学家秦九韶提出了“正负开方术”,提供了一种用算筹布列解任意数字方程的有效算法。你知道吗?相等(1)抛物线与x轴有几个公共点?
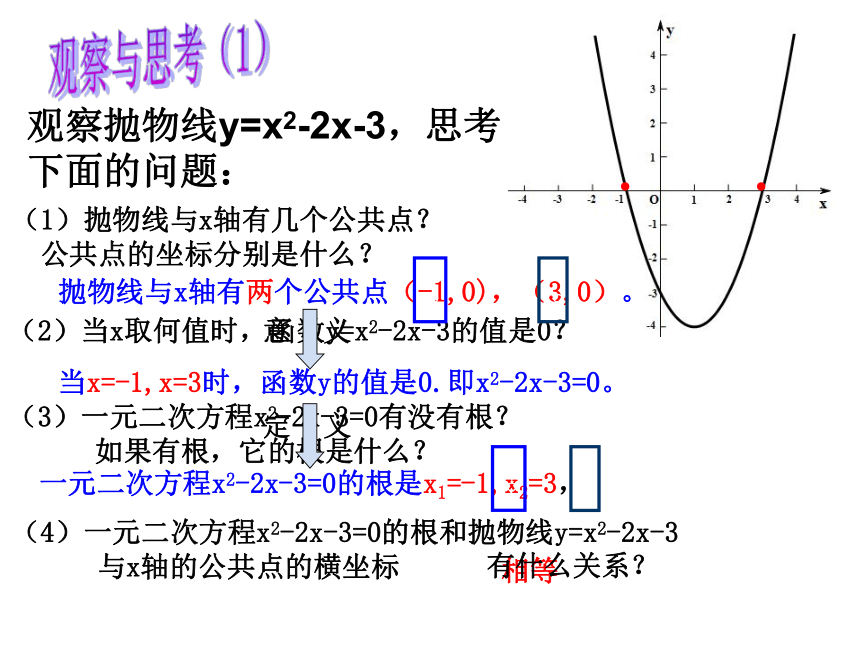
公共点的坐标分别是什么?观察抛物线y=x2-2x-3,思考下面的问题:(2)当x取何值时,函数y=x2-2x-3的值是0?(3)一元二次方程x2-2x-3=0有没有根? 如果有根,它的根是什么?(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3 与x轴的公共点的横坐标观察与思考(1)抛物线与x轴有两个公共点(-1,0),(3,0)。..当x=-1,x=3时,函数y的值是0.即x2-2x-3=0。一元二次方程x2-2x-3=0的根是x1=-1,x2=3,。。。。意 义定 义有什么关系?(1)抛物线与x轴有几个公共点?
交点的坐标分别是什么?观察与思考(2)观察抛物线 ,思考下面的问题:(2)当x取何值时,函数 的值是0?(3)一元二次方程 有没有根?
如果有根,它的根是什么?(4)一元二次方程 的根和抛物线
与x轴的公共点的横坐标有什么关系?定 义意 义。。 相等.y=x2-2x-3(4)一元二次方程x2-2x-3=0的
根和抛物线y=x2-2x-3 与x轴的
公共点的横坐标有什么关系?(4)一元二次方程 的根和抛物线 与x轴的公共点的横坐标有什么关系?通过刚才解答的问题,
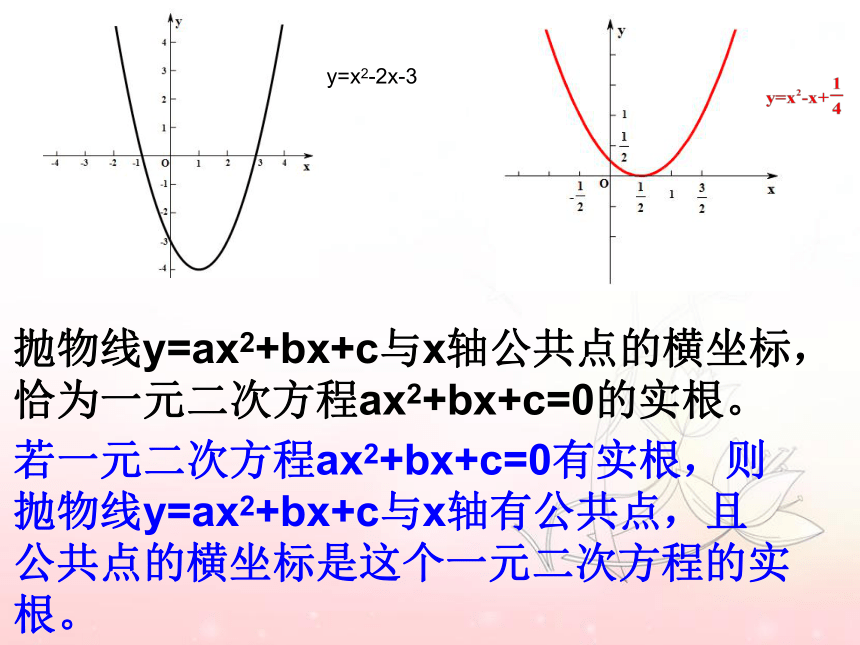
你能得到什么样的结论?抛物线y=ax2+bx+c与x轴公共点的横坐标,
恰为一元二次方程ax2+bx+c=0的实根。若一元二次方程ax2+bx+c=0有实根,则
抛物线y=ax2+bx+c与x轴有公共点,且
公共点的横坐标是这个一元二次方程的实根。y=x2-2x-3抛物线y=ax2+bx+c
与x轴有公共点二次方程ax2+bx+c=0
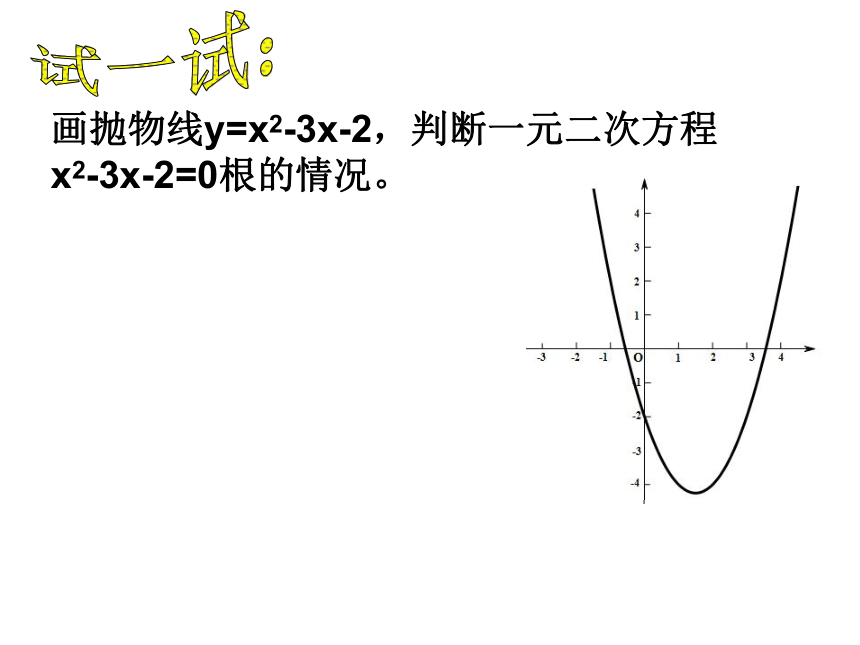
有实根转化为转化为画抛物线y=x2-3x-2,判断一元二次方程x2-3x-2=0根的情况。试一试:例1用图象法讨论一元二次方程x2-3x-2=0的根解:(1)画抛物线y=x2-3x-2.(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.分别计算x=0,x=-1,x=-0.5的函数值,列表如下:xy-1-0.502-0.25-2由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间。由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值(精确到0.1)可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:xy-1.0-0.7-0.9-0.82-0.5-0.61.041.510.160.59-0.25可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5你能求出二次方程
x2-3x-2=0较大根
的近似值吗?试试看!同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:由上表可见,方程的较大根在3.5和3.6之间,
所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6
3.0-0.25-20.163.73.63.51.040.593.93.821.514.0xy例2
用图象法讨论一元二次方程x2-2x+3=0的根。解:(1)画出抛物线y=x2-2x+3
(2)由于图象与x轴没有公共点,所以一元二次方程x2-2x+3=0没有实数根
抛物线y=ax2+bx+c
与x轴无公共点二次方程ax2+bx+c=0
无实根转化为转化为广角镜 对于一元二次方程
ax2+bx+c=0(a,b,c为常数,a≠0), ①
由于一元二次方程的根的个数由代数式b2-4ac的符号决定,因此把b2-4ac叫做一元二次方程根的判别式,通常用希腊字母 表示,即 =b2-4ac 具体来说,一元二次方程的根有三种情况:
(1)当 >0时,方程①有两个不相等的实数根;
(2)当 =0时,方程①有两个相等的实数根;
(3)当 <0时,方程①没有实数根。一元二次方程根的判别式抛物线y=ax2+bx+c
与x轴有公共点二次方程ax2+bx+c=0
有实根二次方程ax2+bx+c=0
的根的判别式 ≥ 0 转化为转化为抛物线y=ax2+bx+c
与x轴无公共点二次方程ax2+bx+c=0
无实根二次方程ax2+bx+c=0
的根的判别式 <0转化为转化为二次函数y=ax2+bx+c的图象二次方程ax2+bx+c=0的根二次函数y=ax2+bx+c的图象与x轴的公共点的个数二次方程ax2+bx+c=0的根的判别式两个公共点一个公共点没有公共点有两个不等实根有两个相等实根没有实根=0>0<0课堂小结:1、二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系。
2、根据二次函数的系数,判断它的图象与x轴的位置关系。
3、利用二次函数的图象求一元二次方程的近似解。课堂小结:当堂检测:2、如果关于x的一元二次方程x2-2x+m=0有
两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与x轴有 个公共点。1、二次方程x2+x-6=0的两根为x1=-3,x2=2,
则二次函数y=x2+x-6的图象与x轴公共点的坐标为 。(-3,0),(2,0)114、用图象法讨论一元二次方程 的根
(精确到0.1)。当堂检测:3、用图象法讨论一元二次方程 的根。01.1330.780.70.60.50.120.450.90.8-0.5-0.20xy17-0.20-0.50.127.37.27.10.780.457.57.41.13xy38计算0与1之间的根:计算7与8之间的根:分析:作业布置:(1)习题5.9 第二题和第三题(2)我们今天所学习的用图象法求一元二次方程的近似解,利用了数形结合及逼近的数学思想,与数学领域的二分法求方程近似解类似,课下有兴趣的同学可以上网查阅资料,了解一下什么是二分法?谢谢大家!小游戏:猜价格礼品盒的价格是0元到12元之间的一个整数,你能快速猜出礼品盒的价格吗?
(规则:在你猜对之前,你每猜出一个价格,只告诉你猜的价格比正确价格高了还是低了)价格在盒子下面!价格:4元。
你猜对了吗?例1
7世纪,隋唐数学家王孝通找出了求三次方程正根的数值解法。
11世纪北宋数学家贾宪以“立成释锁法”解三次或三次以上的高次方程式,同时,还提出了一种更简单的“增乘开方法”。
13世纪,南宋数学家秦九韶提出了“正负开方术”,提供了一种用算筹布列解任意数字方程的有效算法。你知道吗?相等(1)抛物线与x轴有几个公共点?
公共点的坐标分别是什么?观察抛物线y=x2-2x-3,思考下面的问题:(2)当x取何值时,函数y=x2-2x-3的值是0?(3)一元二次方程x2-2x-3=0有没有根? 如果有根,它的根是什么?(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3 与x轴的公共点的横坐标观察与思考(1)抛物线与x轴有两个公共点(-1,0),(3,0)。..当x=-1,x=3时,函数y的值是0.即x2-2x-3=0。一元二次方程x2-2x-3=0的根是x1=-1,x2=3,。。。。意 义定 义有什么关系?(1)抛物线与x轴有几个公共点?
交点的坐标分别是什么?观察与思考(2)观察抛物线 ,思考下面的问题:(2)当x取何值时,函数 的值是0?(3)一元二次方程 有没有根?
如果有根,它的根是什么?(4)一元二次方程 的根和抛物线
与x轴的公共点的横坐标有什么关系?定 义意 义。。 相等.y=x2-2x-3(4)一元二次方程x2-2x-3=0的
根和抛物线y=x2-2x-3 与x轴的
公共点的横坐标有什么关系?(4)一元二次方程 的根和抛物线 与x轴的公共点的横坐标有什么关系?通过刚才解答的问题,
你能得到什么样的结论?抛物线y=ax2+bx+c与x轴公共点的横坐标,
恰为一元二次方程ax2+bx+c=0的实根。若一元二次方程ax2+bx+c=0有实根,则
抛物线y=ax2+bx+c与x轴有公共点,且
公共点的横坐标是这个一元二次方程的实根。y=x2-2x-3抛物线y=ax2+bx+c
与x轴有公共点二次方程ax2+bx+c=0
有实根转化为转化为画抛物线y=x2-3x-2,判断一元二次方程x2-3x-2=0根的情况。试一试:例1用图象法讨论一元二次方程x2-3x-2=0的根解:(1)画抛物线y=x2-3x-2.(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.分别计算x=0,x=-1,x=-0.5的函数值,列表如下:xy-1-0.502-0.25-2由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间。由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值(精确到0.1)可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:xy-1.0-0.7-0.9-0.82-0.5-0.61.041.510.160.59-0.25可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5你能求出二次方程
x2-3x-2=0较大根
的近似值吗?试试看!同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:由上表可见,方程的较大根在3.5和3.6之间,
所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6
3.0-0.25-20.163.73.63.51.040.593.93.821.514.0xy例2
用图象法讨论一元二次方程x2-2x+3=0的根。解:(1)画出抛物线y=x2-2x+3
(2)由于图象与x轴没有公共点,所以一元二次方程x2-2x+3=0没有实数根
抛物线y=ax2+bx+c
与x轴无公共点二次方程ax2+bx+c=0
无实根转化为转化为广角镜 对于一元二次方程
ax2+bx+c=0(a,b,c为常数,a≠0), ①
由于一元二次方程的根的个数由代数式b2-4ac的符号决定,因此把b2-4ac叫做一元二次方程根的判别式,通常用希腊字母 表示,即 =b2-4ac 具体来说,一元二次方程的根有三种情况:
(1)当 >0时,方程①有两个不相等的实数根;
(2)当 =0时,方程①有两个相等的实数根;
(3)当 <0时,方程①没有实数根。一元二次方程根的判别式抛物线y=ax2+bx+c
与x轴有公共点二次方程ax2+bx+c=0
有实根二次方程ax2+bx+c=0
的根的判别式 ≥ 0 转化为转化为抛物线y=ax2+bx+c
与x轴无公共点二次方程ax2+bx+c=0
无实根二次方程ax2+bx+c=0
的根的判别式 <0转化为转化为二次函数y=ax2+bx+c的图象二次方程ax2+bx+c=0的根二次函数y=ax2+bx+c的图象与x轴的公共点的个数二次方程ax2+bx+c=0的根的判别式两个公共点一个公共点没有公共点有两个不等实根有两个相等实根没有实根=0>0<0课堂小结:1、二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系。
2、根据二次函数的系数,判断它的图象与x轴的位置关系。
3、利用二次函数的图象求一元二次方程的近似解。课堂小结:当堂检测:2、如果关于x的一元二次方程x2-2x+m=0有
两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与x轴有 个公共点。1、二次方程x2+x-6=0的两根为x1=-3,x2=2,
则二次函数y=x2+x-6的图象与x轴公共点的坐标为 。(-3,0),(2,0)114、用图象法讨论一元二次方程 的根
(精确到0.1)。当堂检测:3、用图象法讨论一元二次方程 的根。01.1330.780.70.60.50.120.450.90.8-0.5-0.20xy17-0.20-0.50.127.37.27.10.780.457.57.41.13xy38计算0与1之间的根:计算7与8之间的根:分析:作业布置:(1)习题5.9 第二题和第三题(2)我们今天所学习的用图象法求一元二次方程的近似解,利用了数形结合及逼近的数学思想,与数学领域的二分法求方程近似解类似,课下有兴趣的同学可以上网查阅资料,了解一下什么是二分法?谢谢大家!小游戏:猜价格礼品盒的价格是0元到12元之间的一个整数,你能快速猜出礼品盒的价格吗?
(规则:在你猜对之前,你每猜出一个价格,只告诉你猜的价格比正确价格高了还是低了)价格在盒子下面!价格:4元。
你猜对了吗?例1
