北师大版数学九年级下册3.2 圆的对称性教学设计
文档属性
| 名称 | 北师大版数学九年级下册3.2 圆的对称性教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 650.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览



文档简介
北师大版 数学(九年级下册)
第三章 圆
3.2 圆的对称性 教学设计
知识与技能
通过探索理解并掌握:(1)圆的旋转不变性;(2)圆心角、弧、弦之间相等关系的定理。
数学思考
通过动手操作、观察、猜想、归纳,经历探索新知的过程,在数学活动的过程中逐步学会有条理地思考和表达,并培养学生数学基本活动经验。
问题解决
通过对问题的解决,让学生获得分析问题和解决问题的一些基本方法,发展创新意识,进一步培养学生解决问题时的合作能力。
情感态度与价值观
(1)通过引导学生动手操作,对图形的观察发现,激发学生的学习兴趣。
(2)在师生之间、生生之间的合作交流中进一步树立合作意识,培养合作能力,体验获取成功的乐趣,建立学习的自信心。
教学重点:
探索圆心角、弧、弦之间相等关系的定理并利用其解决相关问题。
教学难点:
圆心角、弧、弦之间相等关系定理中的“在同圆或等圆”条件的理解及定理的应用。
教学过程:
一、创设情境,引入新课
在我们的生活中,圆扮演着重要的角色,并成为美的使者和化身,让我们一起来欣赏:(白板出示图片)
向学生展示生活中关于圆的对称性的一些实例,学生欣赏并思考它们的共性,很容易发现圆具有对称性。
教师板书本节课的课题:圆的对称性。
二、合作学习,探究新知:
探究活动一:动手操作,感受圆的对称性
1、巧手折一折,看一看:
(1)圆是轴对称图形吗?
(2)如果是,它的对称轴是什么?
(3)你能找到多少条对称轴?
圆是轴对称图形,其对称轴是任意一条过圆心的直线,有无数条对称轴。
2、巧手转一转,想一想:
(1)一个圆绕着它的圆心旋转任意一个角度,还能与原来的图形重合吗?
(2)如果能重合,那么对称中心是什么?
请观察这两个圆有什么特点
现在把这两个圆叠在一起,使它俩重合,将圆心固定,将上面这个圆旋转任意一个角度,两个圆还重合吗
通过旋转的方法我们知道:圆具有旋转不变的特性。即一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,圆的中心对称性是其旋转不变性的特例,即圆是中心对称图形,对称中心为圆心。
探究活动二:了解圆心角的定义
如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
如:圆心角∠AOB
探究活动三、操作、观察、猜想、说理,初步探索
(1)请利用量角器在准备的同一个圆上画出两个相等且互不重叠的圆心角,分别记作∠AOB和∠A1OB1,并连接弦AB、A1B1。(提醒学生注意:画∠AOB和∠A1OB1时,要使OB相对于OA的方向与OB1相对于OA1的方向一致)
(2)将扇形OAB剪下,将它绕着圆心O旋转,使得OA与OA1重合。
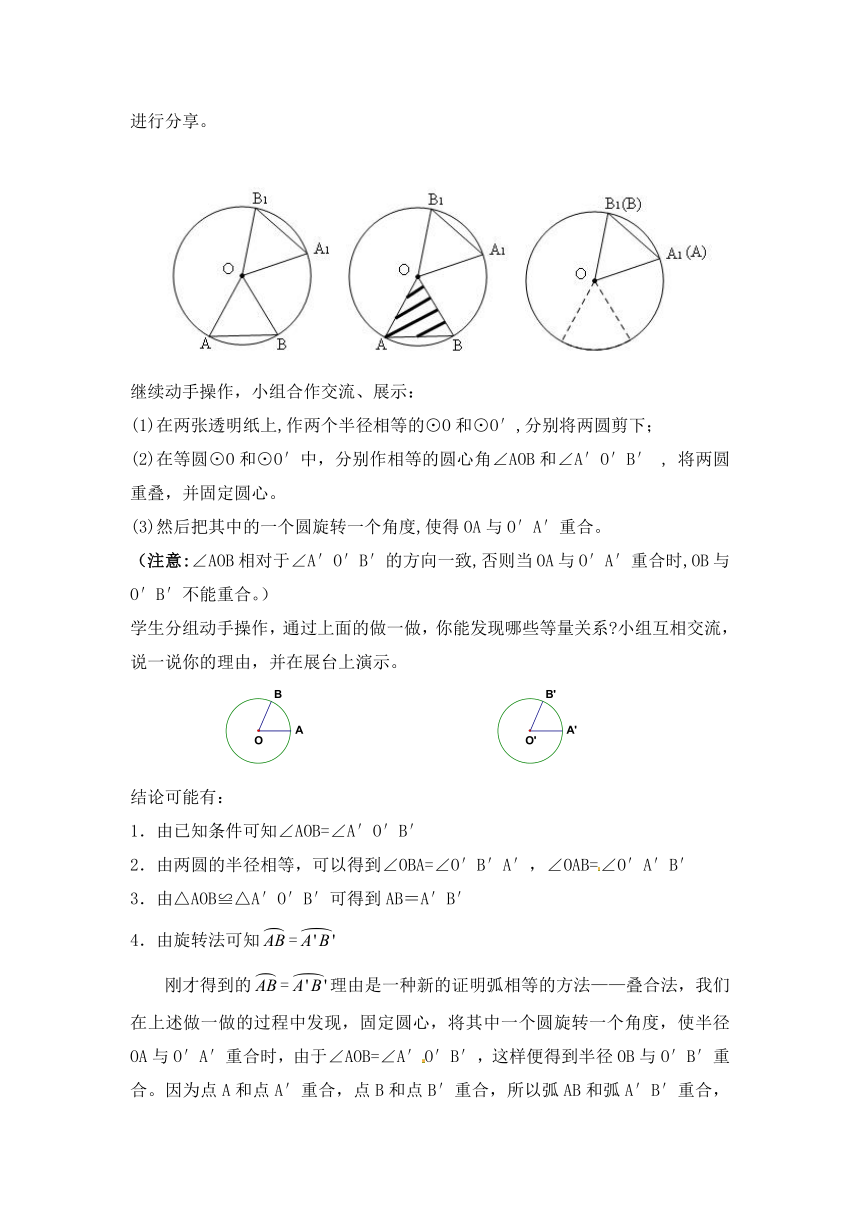
(3)在操作中,仔细观察,你发现了什么?分小组进行合作交流,把各自的想法进行分享。
继续动手操作,小组合作交流、展示:
(1)在两张透明纸上,作两个半径相等的⊙O和⊙O′,分别将两圆剪下;
(2)在等圆⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′ , 将两圆重叠,并固定圆心。
(3)然后把其中的一个圆旋转一个角度,使得OA与O′A′重合。
(注意:∠AOB相对于∠A′O′B′的方向一致,否则当OA与O′A′重合时,OB与O′B′不能重合。)
学生分组动手操作,通过上面的做一做,你能发现哪些等量关系 小组互相交流,说一说你的理由,并在展台上演示。
结论可能有:
1.由已知条件可知∠AOB=∠A′O′B′
2.由两圆的半径相等,可以得到∠OBA=∠O′B′A′,∠OAB=∠O′A′B′
3.由△AOB≌△A′O′B′可得到AB=A′B′
4.由旋转法可知=
刚才得到的=理由是一种新的证明弧相等的方法——叠合法,我们在上述做一做的过程中发现,固定圆心,将其中一个圆旋转一个角度,使半径OA与O′A′重合时,由于∠AOB=∠A′O′B′,这样便得到半径OB与O′B′重合。因为点A和点A′重合,点B和点B′重合,所以弧AB和弧A′B′重合,弦AB与弦A′B′重合,即AB=A′B′。
根据对刚才的操作、观察以及你们所发现的情况,你们能从数学的角度猜想出一个数学结论吗?
在等圆中,相等的圆心角所对的弧相等,所对的弦相等.
上面的结论,在同圆中也成立.于是得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
这就是我们通过实验利用圆的旋转不变性探索到的圆的另一个特性:圆心角、弧、弦之间相等关系定理.
注意:在运用这个定理时,一定不能忘记“在同圆或等圆中”这个前提.否则也不一定有所对的弧相等、弦相等这样的结论.
(通过举反例强化对定理的理解)请同学们画一个只能是圆心角相等的这个条件的图.如下图示.虽然∠AOB=∠A′O′B′,但AB≠A′B′≠,
下面我们共同想一想:
在同圆或等圆中 所对的弧相等
相等的圆心角 所对的弦相等
这个猜想出来的结论对吗?如果正确,你能根据前面所学习的数学知识,对你的这个猜想进行证明吗?请同学们互相讨论,然后尝试着写一写。
在同圆或等圆中,因为∠AOB=∠A′O′B′
所以AB=A′B′,=
探究活动四:思考、探索,形成知识升华
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?
在同圆或等圆中,如果两条弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?为什么?
对于这两个问题,教师应鼓励学生用刚才前面的研究方法,猜一猜,证一证由学生合作探究,并模仿活动三,将两个结论得出。
2、我们上面所涉及的问题都是在同圆或等圆中,都是针对的关于圆心角、圆心角所对的弧与弦的关系,我们发现,它们三者之间,只要有一组量是相等的,其余两个量就都相等了,那你能不能用一句话总结一下?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
注意:(1)不能忽略“在同圆或等圆中”这个前提条件,否则,丢掉这个前提,虽然圆心角相等,但所对的弧、弦不一定相等;
(2)此定理中的“弧”一般指劣弧;
3、我们在做题目的时候通常都需要用数学符号语言来描述,能不能根据所画的图,用数学符号语言把这个结论描述出来?
4、教师指出,今后,在圆中,若要证明圆心角相等、弦相等、弧相等就要想到我们刚刚学习过的知识,即利用圆心角和它所对的弧、弦之间的关系。
归纳小结:(看视频)
三、学以致用,巩固新知
例1、如图,AB,DE是⊙O的直径,C是⊙O的一点,且,BE与CE的大小有什么关系?为什么?
四、课堂练习,强化应用
五、当堂检测:
(
C
1
2
A
B
D
O
)1.如图,在⊙O中, = ,∠1=40°,则∠2=__________
2.如图,点A、B、C、D在⊙O上,AB=DC,AC与BD相等吗?为什么?
3. 如图,在⊙O中, AB=AC,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
(
O
) (
C
) (
B
) (
A
)
六、梳理小结,盘点收获
通过本节课的学习,你收获了哪些知识?
推导本节课知识,你用了哪些数学方法
七、分层作业
A组: 习题3.2 第2题,第3题
B组:习题3.2 第1题,第2题
C组: 习题3.2 第1题
板书设计:
圆的对称性
圆是轴对称图形,也是中心对称图形。
在同圆或等圆中
相等的圆心角
所对的弦相等 所对的弧相等
第三章 圆
3.2 圆的对称性 教学设计
知识与技能
通过探索理解并掌握:(1)圆的旋转不变性;(2)圆心角、弧、弦之间相等关系的定理。
数学思考
通过动手操作、观察、猜想、归纳,经历探索新知的过程,在数学活动的过程中逐步学会有条理地思考和表达,并培养学生数学基本活动经验。
问题解决
通过对问题的解决,让学生获得分析问题和解决问题的一些基本方法,发展创新意识,进一步培养学生解决问题时的合作能力。
情感态度与价值观
(1)通过引导学生动手操作,对图形的观察发现,激发学生的学习兴趣。
(2)在师生之间、生生之间的合作交流中进一步树立合作意识,培养合作能力,体验获取成功的乐趣,建立学习的自信心。
教学重点:
探索圆心角、弧、弦之间相等关系的定理并利用其解决相关问题。
教学难点:
圆心角、弧、弦之间相等关系定理中的“在同圆或等圆”条件的理解及定理的应用。
教学过程:
一、创设情境,引入新课
在我们的生活中,圆扮演着重要的角色,并成为美的使者和化身,让我们一起来欣赏:(白板出示图片)
向学生展示生活中关于圆的对称性的一些实例,学生欣赏并思考它们的共性,很容易发现圆具有对称性。
教师板书本节课的课题:圆的对称性。
二、合作学习,探究新知:
探究活动一:动手操作,感受圆的对称性
1、巧手折一折,看一看:
(1)圆是轴对称图形吗?
(2)如果是,它的对称轴是什么?
(3)你能找到多少条对称轴?
圆是轴对称图形,其对称轴是任意一条过圆心的直线,有无数条对称轴。
2、巧手转一转,想一想:
(1)一个圆绕着它的圆心旋转任意一个角度,还能与原来的图形重合吗?
(2)如果能重合,那么对称中心是什么?
请观察这两个圆有什么特点
现在把这两个圆叠在一起,使它俩重合,将圆心固定,将上面这个圆旋转任意一个角度,两个圆还重合吗
通过旋转的方法我们知道:圆具有旋转不变的特性。即一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,圆的中心对称性是其旋转不变性的特例,即圆是中心对称图形,对称中心为圆心。
探究活动二:了解圆心角的定义
如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.
如:圆心角∠AOB
探究活动三、操作、观察、猜想、说理,初步探索
(1)请利用量角器在准备的同一个圆上画出两个相等且互不重叠的圆心角,分别记作∠AOB和∠A1OB1,并连接弦AB、A1B1。(提醒学生注意:画∠AOB和∠A1OB1时,要使OB相对于OA的方向与OB1相对于OA1的方向一致)
(2)将扇形OAB剪下,将它绕着圆心O旋转,使得OA与OA1重合。
(3)在操作中,仔细观察,你发现了什么?分小组进行合作交流,把各自的想法进行分享。
继续动手操作,小组合作交流、展示:
(1)在两张透明纸上,作两个半径相等的⊙O和⊙O′,分别将两圆剪下;
(2)在等圆⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′ , 将两圆重叠,并固定圆心。
(3)然后把其中的一个圆旋转一个角度,使得OA与O′A′重合。
(注意:∠AOB相对于∠A′O′B′的方向一致,否则当OA与O′A′重合时,OB与O′B′不能重合。)
学生分组动手操作,通过上面的做一做,你能发现哪些等量关系 小组互相交流,说一说你的理由,并在展台上演示。
结论可能有:
1.由已知条件可知∠AOB=∠A′O′B′
2.由两圆的半径相等,可以得到∠OBA=∠O′B′A′,∠OAB=∠O′A′B′
3.由△AOB≌△A′O′B′可得到AB=A′B′
4.由旋转法可知=
刚才得到的=理由是一种新的证明弧相等的方法——叠合法,我们在上述做一做的过程中发现,固定圆心,将其中一个圆旋转一个角度,使半径OA与O′A′重合时,由于∠AOB=∠A′O′B′,这样便得到半径OB与O′B′重合。因为点A和点A′重合,点B和点B′重合,所以弧AB和弧A′B′重合,弦AB与弦A′B′重合,即AB=A′B′。
根据对刚才的操作、观察以及你们所发现的情况,你们能从数学的角度猜想出一个数学结论吗?
在等圆中,相等的圆心角所对的弧相等,所对的弦相等.
上面的结论,在同圆中也成立.于是得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
这就是我们通过实验利用圆的旋转不变性探索到的圆的另一个特性:圆心角、弧、弦之间相等关系定理.
注意:在运用这个定理时,一定不能忘记“在同圆或等圆中”这个前提.否则也不一定有所对的弧相等、弦相等这样的结论.
(通过举反例强化对定理的理解)请同学们画一个只能是圆心角相等的这个条件的图.如下图示.虽然∠AOB=∠A′O′B′,但AB≠A′B′≠,
下面我们共同想一想:
在同圆或等圆中 所对的弧相等
相等的圆心角 所对的弦相等
这个猜想出来的结论对吗?如果正确,你能根据前面所学习的数学知识,对你的这个猜想进行证明吗?请同学们互相讨论,然后尝试着写一写。
在同圆或等圆中,因为∠AOB=∠A′O′B′
所以AB=A′B′,=
探究活动四:思考、探索,形成知识升华
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?
在同圆或等圆中,如果两条弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?为什么?
对于这两个问题,教师应鼓励学生用刚才前面的研究方法,猜一猜,证一证由学生合作探究,并模仿活动三,将两个结论得出。
2、我们上面所涉及的问题都是在同圆或等圆中,都是针对的关于圆心角、圆心角所对的弧与弦的关系,我们发现,它们三者之间,只要有一组量是相等的,其余两个量就都相等了,那你能不能用一句话总结一下?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
注意:(1)不能忽略“在同圆或等圆中”这个前提条件,否则,丢掉这个前提,虽然圆心角相等,但所对的弧、弦不一定相等;
(2)此定理中的“弧”一般指劣弧;
3、我们在做题目的时候通常都需要用数学符号语言来描述,能不能根据所画的图,用数学符号语言把这个结论描述出来?
4、教师指出,今后,在圆中,若要证明圆心角相等、弦相等、弧相等就要想到我们刚刚学习过的知识,即利用圆心角和它所对的弧、弦之间的关系。
归纳小结:(看视频)
三、学以致用,巩固新知
例1、如图,AB,DE是⊙O的直径,C是⊙O的一点,且,BE与CE的大小有什么关系?为什么?
四、课堂练习,强化应用
五、当堂检测:
(
C
1
2
A
B
D
O
)1.如图,在⊙O中, = ,∠1=40°,则∠2=__________
2.如图,点A、B、C、D在⊙O上,AB=DC,AC与BD相等吗?为什么?
3. 如图,在⊙O中, AB=AC,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
(
O
) (
C
) (
B
) (
A
)
六、梳理小结,盘点收获
通过本节课的学习,你收获了哪些知识?
推导本节课知识,你用了哪些数学方法
七、分层作业
A组: 习题3.2 第2题,第3题
B组:习题3.2 第1题,第2题
C组: 习题3.2 第1题
板书设计:
圆的对称性
圆是轴对称图形,也是中心对称图形。
在同圆或等圆中
相等的圆心角
所对的弦相等 所对的弧相等
