北师大版数学九年级下册3.6直线和圆的位置关系第2课时教学设计
文档属性
| 名称 | 北师大版数学九年级下册3.6直线和圆的位置关系第2课时教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 96.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览

文档简介
第2课时 直线和圆的位置关系
教学目标:
知识与技能
1.掌握切线的判定定理,能判定一条直线是否为圆的切线;
2.掌握切线的性质定理;
过程与方法:
经历探究切线的判定方法,培养学生学数学,用数学的意识;
能综合运用圆的切线的判定和性质解决问题.
情感态度价值观
能过对圆的切线的判定方法的探究,引导学生既能独立思考问题,同时也能积极参与讨论,培养学生合作学习、共同进步;
培养学生进行几何推理,数形结合的思想。
重点难点:
1.探索圆的切线的判定和性质,并能运用(重点).
2.探索圆的切线的判定方法(难点).
教学过程:
在纸上画一个⊙O和圆上一点A,根据所学知识,如何画出这个圆的过点A的一条切线?
⑴能画几条?
⑵有几种画法?
⑶你怎么确定你所画的这条直线是⊙O的切线?
这就是这节课要研究的问题——切线的判断.
复习旧知
直线和圆的位置关系的判定方法
1、判断 (1)直线与圆最多有两个公共点. ( )
(2)若直线与圆相交,则直线上的点都在圆内.( )
(3)若A是⊙O上一点,则直线AB与⊙O相切.( )
(4)若C为⊙O外的一点,则过点C的直线CD与⊙O相交或相离。( )
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
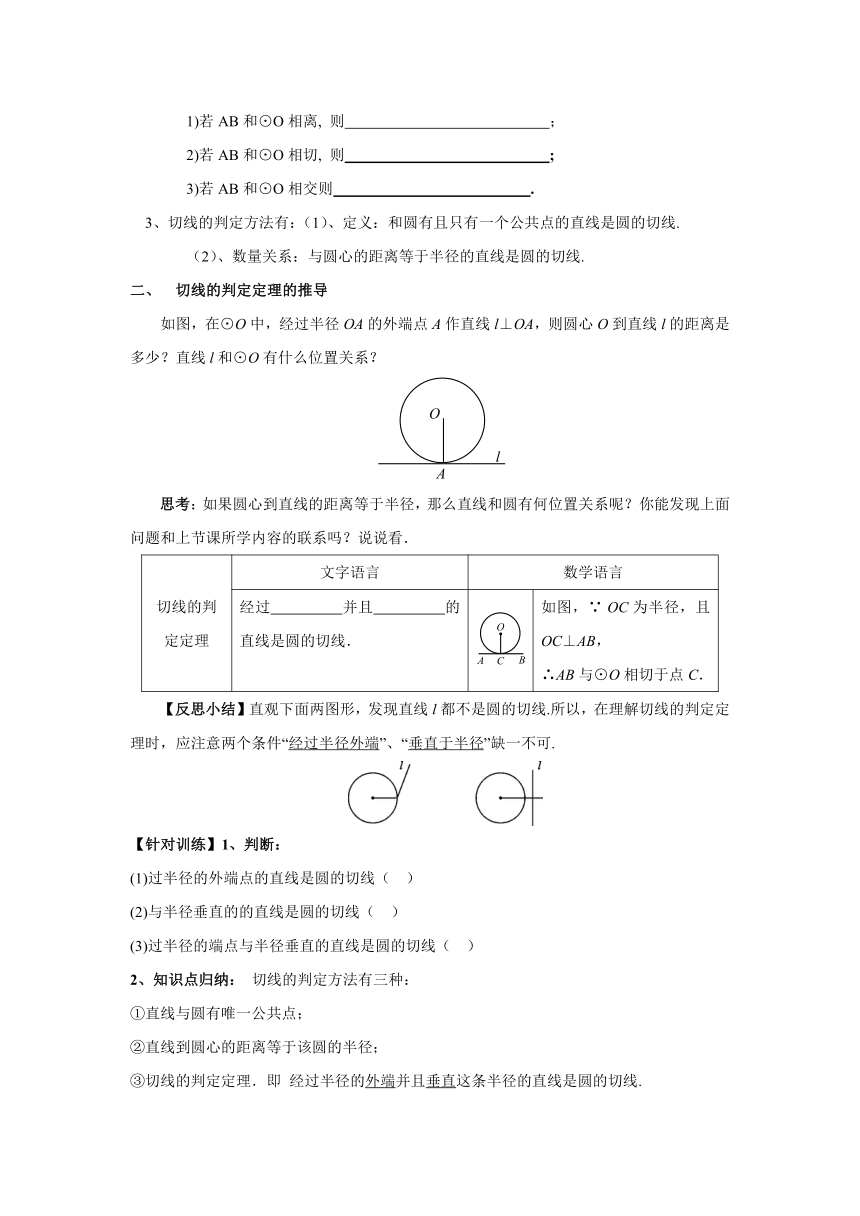
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交则 .
3、切线的判定方法有:(1)、定义:和圆有且只有一个公共点的直线是圆的切线.
(2)、数量关系:与圆心的距离等于半径的直线是圆的切线.
二、 切线的判定定理的推导
如图,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?
(
l
O
A
)
思考:如果圆心到直线的距离等于半径,那么直线和圆有何位置关系呢?你能发现上面问题和上节课所学内容的联系吗?说说看.
切线的判定定理 文字语言 数学语言
经过 并且 的直线是圆的切线. (
O
A
C
B
) 如图,∵ OC为半径,且OC⊥AB, ∴AB与⊙O相切于点C.
【反思小结】直观下面两图形,发现直线l都不是圆的切线.所以,在理解切线的判定定理时,应注意两个条件“经过半径外端”、“垂直于半径”缺一不可.
【针对训练】1、判断:
(1)过半径的外端点的直线是圆的切线( )
(2)与半径垂直的的直线是圆的切线( )
(3)过半径的端点与半径垂直的直线是圆的切线( )
2、知识点归纳: 切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即 经过半径的外端并且垂直这条半径的直线是圆的切线.
三、 切线判定定理的应用
例1?如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证直线AB是⊙O的切线.? ???
思考: AB已经过⊙O上的点C,如果连接OC,那么就满足了"经过半径的外端"这一条件,接着根据切线的判定定理,只要再证明什么即可?
【反思小结】证明某直线与圆相切时,如果已知直线与圆有公共点,即可作出过该点的半径,证明直线垂直于该半径,即“知半径,证垂直”.
例2 如图,已知OC平分∠AOB,点D是OC上任意一点,⊙D与OA相切于点E,求证:OB与⊙D相切.
思考:如果过点O作DF垂直OB,那么就满足了"垂直于这条直线"这一条件,接着根据切线的判定定理,只要再证明什么即可?
【反思小结】证明某直线与圆相切时, 当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.
【针对训练】
1、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
2、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.求证:AB是⊙O的切线.
合作探究:生活中的数学
1. 当你在下雨天,快速转动雨伞时水飞出的方向是什么方向?
2. 砂轮打磨工件飞出火星的方向是什么方向?
四、课堂小结问题:
1.两个定理:切线的判定定理是 .
切线的性质定理是 .
2.数学思想方法:
(1)证明切线的性质定理所用的方法是反证法.
(2)证明切线的方法:
①当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“连半径,证垂直”.
②当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.
(3)在运用切线的性质时,连接圆心和切点是常作的辅助线,这样可以产生半径和垂直条件.
五、课后作业
完成对应练习
教学目标:
知识与技能
1.掌握切线的判定定理,能判定一条直线是否为圆的切线;
2.掌握切线的性质定理;
过程与方法:
经历探究切线的判定方法,培养学生学数学,用数学的意识;
能综合运用圆的切线的判定和性质解决问题.
情感态度价值观
能过对圆的切线的判定方法的探究,引导学生既能独立思考问题,同时也能积极参与讨论,培养学生合作学习、共同进步;
培养学生进行几何推理,数形结合的思想。
重点难点:
1.探索圆的切线的判定和性质,并能运用(重点).
2.探索圆的切线的判定方法(难点).
教学过程:
在纸上画一个⊙O和圆上一点A,根据所学知识,如何画出这个圆的过点A的一条切线?
⑴能画几条?
⑵有几种画法?
⑶你怎么确定你所画的这条直线是⊙O的切线?
这就是这节课要研究的问题——切线的判断.
复习旧知
直线和圆的位置关系的判定方法
1、判断 (1)直线与圆最多有两个公共点. ( )
(2)若直线与圆相交,则直线上的点都在圆内.( )
(3)若A是⊙O上一点,则直线AB与⊙O相切.( )
(4)若C为⊙O外的一点,则过点C的直线CD与⊙O相交或相离。( )
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交则 .
3、切线的判定方法有:(1)、定义:和圆有且只有一个公共点的直线是圆的切线.
(2)、数量关系:与圆心的距离等于半径的直线是圆的切线.
二、 切线的判定定理的推导
如图,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?
(
l
O
A
)
思考:如果圆心到直线的距离等于半径,那么直线和圆有何位置关系呢?你能发现上面问题和上节课所学内容的联系吗?说说看.
切线的判定定理 文字语言 数学语言
经过 并且 的直线是圆的切线. (
O
A
C
B
) 如图,∵ OC为半径,且OC⊥AB, ∴AB与⊙O相切于点C.
【反思小结】直观下面两图形,发现直线l都不是圆的切线.所以,在理解切线的判定定理时,应注意两个条件“经过半径外端”、“垂直于半径”缺一不可.
【针对训练】1、判断:
(1)过半径的外端点的直线是圆的切线( )
(2)与半径垂直的的直线是圆的切线( )
(3)过半径的端点与半径垂直的直线是圆的切线( )
2、知识点归纳: 切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即 经过半径的外端并且垂直这条半径的直线是圆的切线.
三、 切线判定定理的应用
例1?如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证直线AB是⊙O的切线.? ???
思考: AB已经过⊙O上的点C,如果连接OC,那么就满足了"经过半径的外端"这一条件,接着根据切线的判定定理,只要再证明什么即可?
【反思小结】证明某直线与圆相切时,如果已知直线与圆有公共点,即可作出过该点的半径,证明直线垂直于该半径,即“知半径,证垂直”.
例2 如图,已知OC平分∠AOB,点D是OC上任意一点,⊙D与OA相切于点E,求证:OB与⊙D相切.
思考:如果过点O作DF垂直OB,那么就满足了"垂直于这条直线"这一条件,接着根据切线的判定定理,只要再证明什么即可?
【反思小结】证明某直线与圆相切时, 当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.
【针对训练】
1、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
2、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.求证:AB是⊙O的切线.
合作探究:生活中的数学
1. 当你在下雨天,快速转动雨伞时水飞出的方向是什么方向?
2. 砂轮打磨工件飞出火星的方向是什么方向?
四、课堂小结问题:
1.两个定理:切线的判定定理是 .
切线的性质定理是 .
2.数学思想方法:
(1)证明切线的性质定理所用的方法是反证法.
(2)证明切线的方法:
①当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“连半径,证垂直”.
②当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.
(3)在运用切线的性质时,连接圆心和切点是常作的辅助线,这样可以产生半径和垂直条件.
五、课后作业
完成对应练习
