第二十二章 二次函数专题卷B——核心考点归纳一点通(含答案)
文档属性
| 名称 | 第二十二章 二次函数专题卷B——核心考点归纳一点通(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 325.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 10:01:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
8.九年级数学(上)第22章《二次函数》专题卷B——核心思想方法归纳一点通
核心考点1 二次函数与面积
方法归纳1 面积→方程→坐标
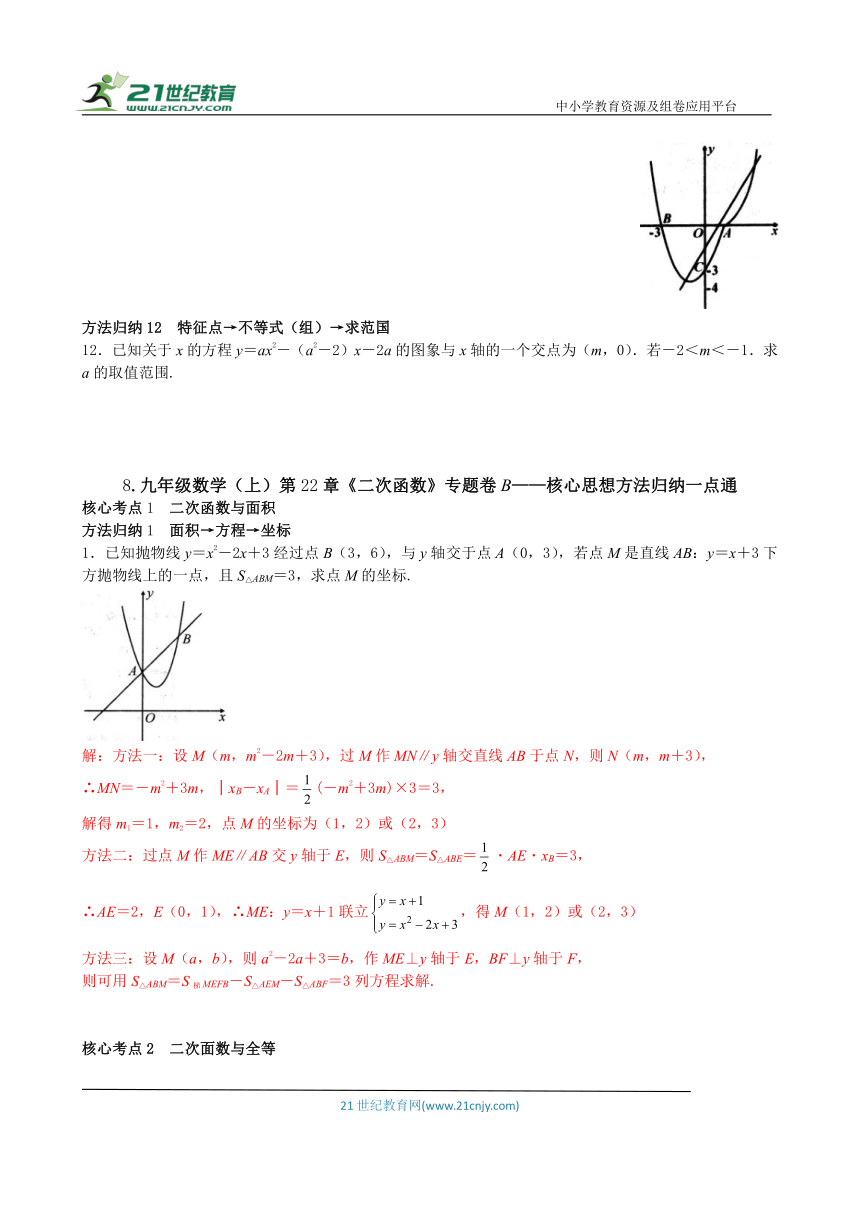
1.已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
核心考点2 二次面数与全等
方法归纳2 全等→等线段→方程→坐标
2.如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A,B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
核心考点3 二次函数与勾股定理
方法归的3 勾股→方程→坐标
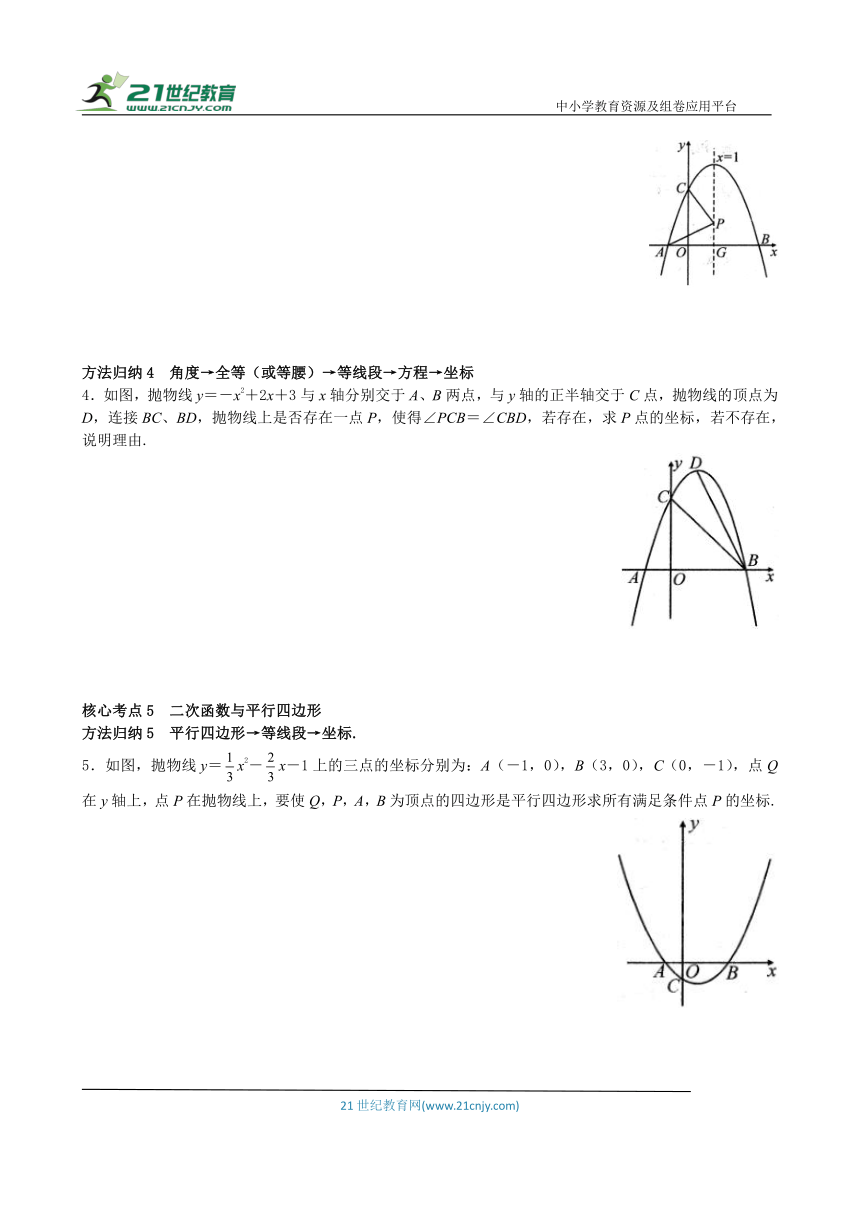
3.如图,抛物线y=ax2+bx+3交x轴于点A,B,点A的坐标为(-1,0),交y轴于点C,其对称轴为x=1.
(1)求抛物线的解析式.
(2)点P为直线x=1上一点,当PA=PC时,求y点P的坐标.
方法归纳4 角度→全等(或等腰)→等线段→方程→坐标
4.如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD,若存在,求P点的坐标,若不存在,说明理由.
核心考点5 二次函数与平行四边形
方法归纳5 平行四边形→等线段→坐标.
5.如图,抛物线y=x2-x-1上的三点的坐标分别为:A(-1,0),B(3,0),C(0,-1),点Q在y轴上,点P在抛物线上,要使Q,P,A,B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
核心考点6 二次函数与根的判别式
方法归纳6 联立消y→判别式→求参数
抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,已知点B的坐标为(4,0),直线∥BC且与该抛物线有唯一公共点M,求点M的坐标.
核心考点7 二次函数与根与系数的关系
方法归纳7 联立消y→根与系数的关系→求参数
7.已知抛物线y=-x2-2x+3与x轴交于A,B(1,0)两点,与y轴交于点C(0,3),将直线BC向下平移,与抛物线交于点B',C'(B与B'对应,C与C'对应),与y轴交于点D,当点D是线段B'C'的三等分点时,求点D的坐标.
核心考点8 二次函数与最值
方法归納8 设参数→几何性质→二次函数→最值
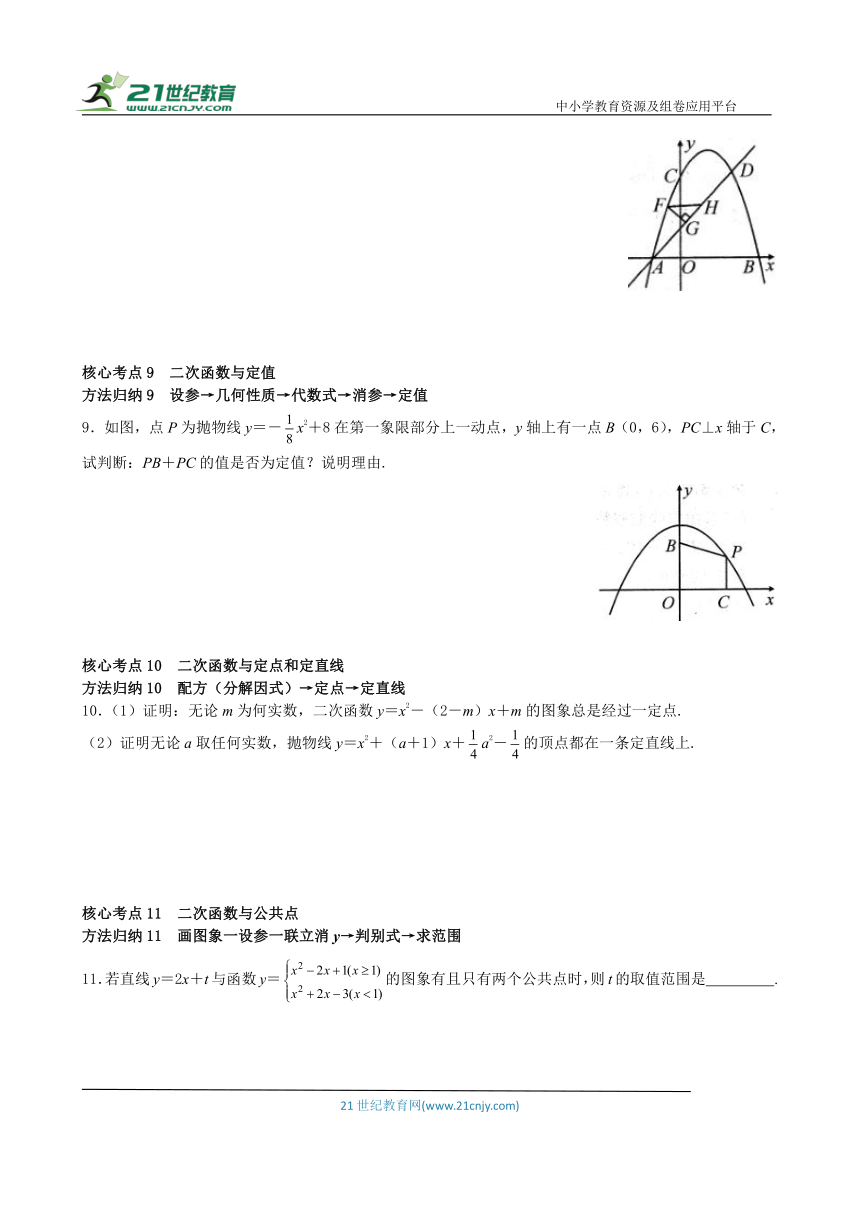
8.如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,直线y=x+1过点A,交抛物线于另一点D.在AD上方抛物线上有一点F,过点F作FG⊥AD于G,作FH∥x轴交直线AD于H,求△FGH的周长的最大值
核心考点9 二次函数与定值
方法归纳9 设参→几何性质→代数式→消参→定值
9.如图,点P为抛物线y=-x2+8在第一象限部分上一动点,y轴上有一点B(0,6),PC⊥x轴于C,试判断:PB+PC的值是否为定值?说明理由.
核心考点10 二次函数与定点和定直线
方法归纳10 配方(分解因式)→定点→定直线
10.(1)证明:无论m为何实数,二次函数y=x2-(2-m)x+m的图象总是经过一定点.
(2)证明无论a取任何实数,抛物线y=x2+(a+1)x+a2-的顶点都在一条定直线上.
核心考点11 二次函数与公共点
方法归纳11 画图象一设参一联立消y→判别式→求范围
11.若直线y=2x+t与函数y=的图象有且只有两个公共点时,则t的取值范围是 .
方法归纳12 特征点→不等式(组)→求范国
12.已知关于x的方程y=ax2-(a2-2)x-2a的图象与x轴的一个交点为(m,0).若-2<m<-1.求a的取值范围.
8.九年级数学(上)第22章《二次函数》专题卷B——核心思想方法归纳一点通
核心考点1 二次函数与面积
方法归纳1 面积→方程→坐标
1.已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
解:方法一:设M(m,m2-2m+3),过M作MN∥y轴交直线AB于点N,则N(m,m+3),
∴MN=-m2+3m,│xB-xA│=(-m2+3m)×3=3,
解得m1=1,m2=2,点M的坐标为(1,2)或(2,3)
方法二:过点M作ME∥AB交y轴于E,则S△ABM=S△ABE= AE xB=3,
∴AE=2,E(0,1),∴ME:y=x+1联立,得M(1,2)或(2,3)
方法三:设M(a,b),则a2-2a+3=b,作ME⊥y轴于E,BF⊥y轴于F,
则可用S△ABM=S梯MEFB-S△AEM-S△ABF=3列方程求解.
核心考点2 二次面数与全等
方法归纳2 全等→等线段→方程→坐标
2.如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A,B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
解:易求y=-x2+4x-3,C(0、-3),M(2,1),作ME⊥y轴于E,作PF⊥x轴于F,
易证△PDF≌△CME,∴PF=CE=4,∴yp=-4,
由-x2+4x-3=-4得xp=2+,∴P(2+,-4).
核心考点3 二次函数与勾股定理
方法归的3 勾股→方程→坐标
3.如图,抛物线y=ax2+bx+3交x轴于点A,B,点A的坐标为(-1,0),交y轴于点C,其对称轴为x=1.
(1)求抛物线的解析式.
(2)点P为直线x=1上一点,当PA=PC时,求y点P的坐标.
解:(1)=-x2+2x+3
(2)设直线x=1与x轴交于点G,过点C作CH⊥PG,垂足为H,HG=OC=3,
设P(1,m),在Rt△APG中,AG=2,PG=m,AP2=m2+4,
在RI△CPH中,PC2=CH+PH2=12+(3m)2=m2-6m+10,
∵PA=PC,∴4+m2=m2-6m+10,m=1,∴P(1,1)
方法归纳4 角度→全等(或等腰)→等线段→方程→坐标
4.如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD,若存在,求P点的坐标,若不存在,说明理由.
解:(,)点(4,-5),分两种情况:
①作∠BCP1=∠CBD交第四象限的物线于P1,则CP1∥BD,∵B(3,0),C(0,3),D(1,4),BD:y=-2x+6,易求:CP1:y=-2x+3,联立得P1(4,-5).
②作∠BCP2=∠CBD交第一象限的抛物线于P2交x轴于E,设直线BD交y轴于F,易证∠∠OBD=∠OCE,△OCE≌△OBF,∵F(0,6),∴E(6,0),∴CE:y=-x+3,联立,得P2(,)
核心考点5 二次函数与平行四边形
方法归纳5 平行四边形→等线段→坐标.
5.如图,抛物线y=x2-x-1上的三点的坐标分别为:A(-1,0),B(3,0),C(0,-1),点Q在y轴上,点P在抛物线上,要使Q,P,A,B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
解:①AB为边时,只要PQ∥AB且PQ=AB=4即可,
又知点Q在y轴上,点P的横坐标为4或-4,
这时合条件的点P有两个,分别记为P1,P2,
而当x=4时,y=;当x=-4时,y=7,此时P1(4,),P2(-4,7).
②当AB为对角线时,只要线段PQ与线段AB互相平分即可,
又知点Q在y轴上,且线段AB中点的横坐标为1,
∴点P的横坐标为2,这时符合条件的P只有一个记为P3,
而且当x=2时y=-1,此时P(2,-1),
满足条件的P为P1(4,),P2(-4,7),P3(2,-1).
核心考点6 二次函数与根的判别式
方法归纳6 联立消y→判别式→求参数
抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,已知点B的坐标为(4,0),直线∥BC且与该抛物线有唯一公共点M,求点M的坐标.
解:可得直线BC的解析式为y=x-2,直线l∥BC,则该直线的解析式可表示为y=x+b。当直线l与抛物线只有一个交点时,可列方程x+b=x2-x-2,由△=0,知b=-4.联立方程组可求交点M(2,-3).
核心考点7 二次函数与根与系数的关系
方法归纳7 联立消y→根与系数的关系→求参数
7.已知抛物线y=-x2-2x+3与x轴交于A,B(1,0)两点,与y轴交于点C(0,3),将直线BC向下平移,与抛物线交于点B',C'(B与B'对应,C与C'对应),与y轴交于点D,当点D是线段B'C'的三等分点时,求点D的坐标.
解:BC的解析式为y=-3x+3,设直线B'C'的解析式为y=-3x+t ,
则D(0,t)由得x2-x+t-3=0,
设B'(x1,y1),C'(x2,y2),则x1+x2=1,x1x2=t-3,
∵点D是线段B'C'的三等分点,∴x2=-3x1或x1=-3x2;
当x2=3x1时,x1-3x1=1,求出t=,D点坐标为(0,);
当x1=-3x2时;-3x2+x2=1,∴x2=-(不符合题意,舍去),∴D(0,)
核心考点8 二次函数与最值
方法归納8 设参数→几何性质→二次函数→最值
8.如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,直线y=x+1过点A,交抛物线于另一点D.在AD上方抛物线上有一点F,过点F作FG⊥AD于G,作FH∥x轴交直线AD于H,求△FGH的周长的最大值
解:思路一:∠DAB=45°,△FGH为等腰直角三角形,FG: HG: FH=1:1:2,
设F(m,-m2+m+3),把y=-m2+2m+3
代入y=x+1,xH=-m2+2m+2,FH=-m2+2m+2-m=-m2+m+2,
C△FGH=FH+FG+HG=(+1)FH=-(+1)(m-)2+,
当m=时,△FGH周长的最大值为.
思路二:将直线AD向上平移至与抛物线只有一个公共F时,FG最大,故△FGH周长最大,再用判别式△=0求解.
核心考点9 二次函数与定值
方法归纳9 设参→几何性质→代数式→消参→定值
9.如图,点P为抛物线y=-x2+8在第一象限部分上一动点,y轴上有一点B(0,6),PC⊥x轴于C,试判断:PB+PC的值是否为定值?说明理由.
解;过点P作PQ⊥y轴于Q.设P(x,x2+8),
则PQ=x,PC=x2+8,PB=x2+2,PB+PC=10,故PB+PC的值为定值.
核心考点10 二次函数与定点和定直线
方法归纳10 配方(分解因式)→定点→定直线
10.(1)证明:无论m为何实数,二次函数y=x2-(2-m)x+m的图象总是经过一定点.
(2)证明无论a取任何实数,抛物线y=x2+(a+1)x+a2-的顶点都在一条定直线上.
证明:(1)可证x=-1时,y=3,故图早过定点(-1,3)
(2)可得项点(-,-),故顶点在直线y=x上.
核心考点11 二次函数与公共点
方法归纳11 画图象一设参一联立消y→判别式→求范围
11.若直线y=2x+t与函数y=的图象有且只有两个公共点时,则t的取值范围是t=-3或t>-2
解:如图,图象与x交于A(1,0),B(-3,0),与y轴交于C(0,-3),
①当直线y=2x+t过点A(1,0)时,t=-2,此时图象与直y=2x+t有3个公点,
②由得:x2-4x+1-t=0,△=16-4(1-t)=0,t=-3,由得:x2-3-t=0,△=0-4(-3-t)=0.t=-3,当t=-3时,图象与直线y=2x+t只有两个公共点:
综上所述,t的取值范围是t=-3或t>-2
方法归纳12 特征点→不等式(组)→求范国
12.已知关于x的方程y=ax2-(a2-2)x-2a的图象与x轴的一个交点为(m,0).若-2<m<-1.求a的取值范围.
解:今y=0,得-(a2-2)x-2a=0,得x1=a,x2=,
①当a>0时,-2<<-1,得1<a<2,
②当a<0时,-2<a<-1.
综上a的范围为1<a<2或-2<a<-1
21世纪教育网(www.21cnjy.com)
8.九年级数学(上)第22章《二次函数》专题卷B——核心思想方法归纳一点通
核心考点1 二次函数与面积
方法归纳1 面积→方程→坐标
1.已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
核心考点2 二次面数与全等
方法归纳2 全等→等线段→方程→坐标
2.如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A,B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
核心考点3 二次函数与勾股定理
方法归的3 勾股→方程→坐标
3.如图,抛物线y=ax2+bx+3交x轴于点A,B,点A的坐标为(-1,0),交y轴于点C,其对称轴为x=1.
(1)求抛物线的解析式.
(2)点P为直线x=1上一点,当PA=PC时,求y点P的坐标.
方法归纳4 角度→全等(或等腰)→等线段→方程→坐标
4.如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD,若存在,求P点的坐标,若不存在,说明理由.
核心考点5 二次函数与平行四边形
方法归纳5 平行四边形→等线段→坐标.
5.如图,抛物线y=x2-x-1上的三点的坐标分别为:A(-1,0),B(3,0),C(0,-1),点Q在y轴上,点P在抛物线上,要使Q,P,A,B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
核心考点6 二次函数与根的判别式
方法归纳6 联立消y→判别式→求参数
抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,已知点B的坐标为(4,0),直线∥BC且与该抛物线有唯一公共点M,求点M的坐标.
核心考点7 二次函数与根与系数的关系
方法归纳7 联立消y→根与系数的关系→求参数
7.已知抛物线y=-x2-2x+3与x轴交于A,B(1,0)两点,与y轴交于点C(0,3),将直线BC向下平移,与抛物线交于点B',C'(B与B'对应,C与C'对应),与y轴交于点D,当点D是线段B'C'的三等分点时,求点D的坐标.
核心考点8 二次函数与最值
方法归納8 设参数→几何性质→二次函数→最值
8.如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,直线y=x+1过点A,交抛物线于另一点D.在AD上方抛物线上有一点F,过点F作FG⊥AD于G,作FH∥x轴交直线AD于H,求△FGH的周长的最大值
核心考点9 二次函数与定值
方法归纳9 设参→几何性质→代数式→消参→定值
9.如图,点P为抛物线y=-x2+8在第一象限部分上一动点,y轴上有一点B(0,6),PC⊥x轴于C,试判断:PB+PC的值是否为定值?说明理由.
核心考点10 二次函数与定点和定直线
方法归纳10 配方(分解因式)→定点→定直线
10.(1)证明:无论m为何实数,二次函数y=x2-(2-m)x+m的图象总是经过一定点.
(2)证明无论a取任何实数,抛物线y=x2+(a+1)x+a2-的顶点都在一条定直线上.
核心考点11 二次函数与公共点
方法归纳11 画图象一设参一联立消y→判别式→求范围
11.若直线y=2x+t与函数y=的图象有且只有两个公共点时,则t的取值范围是 .
方法归纳12 特征点→不等式(组)→求范国
12.已知关于x的方程y=ax2-(a2-2)x-2a的图象与x轴的一个交点为(m,0).若-2<m<-1.求a的取值范围.
8.九年级数学(上)第22章《二次函数》专题卷B——核心思想方法归纳一点通
核心考点1 二次函数与面积
方法归纳1 面积→方程→坐标
1.已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
解:方法一:设M(m,m2-2m+3),过M作MN∥y轴交直线AB于点N,则N(m,m+3),
∴MN=-m2+3m,│xB-xA│=(-m2+3m)×3=3,
解得m1=1,m2=2,点M的坐标为(1,2)或(2,3)
方法二:过点M作ME∥AB交y轴于E,则S△ABM=S△ABE= AE xB=3,
∴AE=2,E(0,1),∴ME:y=x+1联立,得M(1,2)或(2,3)
方法三:设M(a,b),则a2-2a+3=b,作ME⊥y轴于E,BF⊥y轴于F,
则可用S△ABM=S梯MEFB-S△AEM-S△ABF=3列方程求解.
核心考点2 二次面数与全等
方法归纳2 全等→等线段→方程→坐标
2.如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A,B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
解:易求y=-x2+4x-3,C(0、-3),M(2,1),作ME⊥y轴于E,作PF⊥x轴于F,
易证△PDF≌△CME,∴PF=CE=4,∴yp=-4,
由-x2+4x-3=-4得xp=2+,∴P(2+,-4).
核心考点3 二次函数与勾股定理
方法归的3 勾股→方程→坐标
3.如图,抛物线y=ax2+bx+3交x轴于点A,B,点A的坐标为(-1,0),交y轴于点C,其对称轴为x=1.
(1)求抛物线的解析式.
(2)点P为直线x=1上一点,当PA=PC时,求y点P的坐标.
解:(1)=-x2+2x+3
(2)设直线x=1与x轴交于点G,过点C作CH⊥PG,垂足为H,HG=OC=3,
设P(1,m),在Rt△APG中,AG=2,PG=m,AP2=m2+4,
在RI△CPH中,PC2=CH+PH2=12+(3m)2=m2-6m+10,
∵PA=PC,∴4+m2=m2-6m+10,m=1,∴P(1,1)
方法归纳4 角度→全等(或等腰)→等线段→方程→坐标
4.如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD,若存在,求P点的坐标,若不存在,说明理由.
解:(,)点(4,-5),分两种情况:
①作∠BCP1=∠CBD交第四象限的物线于P1,则CP1∥BD,∵B(3,0),C(0,3),D(1,4),BD:y=-2x+6,易求:CP1:y=-2x+3,联立得P1(4,-5).
②作∠BCP2=∠CBD交第一象限的抛物线于P2交x轴于E,设直线BD交y轴于F,易证∠∠OBD=∠OCE,△OCE≌△OBF,∵F(0,6),∴E(6,0),∴CE:y=-x+3,联立,得P2(,)
核心考点5 二次函数与平行四边形
方法归纳5 平行四边形→等线段→坐标.
5.如图,抛物线y=x2-x-1上的三点的坐标分别为:A(-1,0),B(3,0),C(0,-1),点Q在y轴上,点P在抛物线上,要使Q,P,A,B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
解:①AB为边时,只要PQ∥AB且PQ=AB=4即可,
又知点Q在y轴上,点P的横坐标为4或-4,
这时合条件的点P有两个,分别记为P1,P2,
而当x=4时,y=;当x=-4时,y=7,此时P1(4,),P2(-4,7).
②当AB为对角线时,只要线段PQ与线段AB互相平分即可,
又知点Q在y轴上,且线段AB中点的横坐标为1,
∴点P的横坐标为2,这时符合条件的P只有一个记为P3,
而且当x=2时y=-1,此时P(2,-1),
满足条件的P为P1(4,),P2(-4,7),P3(2,-1).
核心考点6 二次函数与根的判别式
方法归纳6 联立消y→判别式→求参数
抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,已知点B的坐标为(4,0),直线∥BC且与该抛物线有唯一公共点M,求点M的坐标.
解:可得直线BC的解析式为y=x-2,直线l∥BC,则该直线的解析式可表示为y=x+b。当直线l与抛物线只有一个交点时,可列方程x+b=x2-x-2,由△=0,知b=-4.联立方程组可求交点M(2,-3).
核心考点7 二次函数与根与系数的关系
方法归纳7 联立消y→根与系数的关系→求参数
7.已知抛物线y=-x2-2x+3与x轴交于A,B(1,0)两点,与y轴交于点C(0,3),将直线BC向下平移,与抛物线交于点B',C'(B与B'对应,C与C'对应),与y轴交于点D,当点D是线段B'C'的三等分点时,求点D的坐标.
解:BC的解析式为y=-3x+3,设直线B'C'的解析式为y=-3x+t ,
则D(0,t)由得x2-x+t-3=0,
设B'(x1,y1),C'(x2,y2),则x1+x2=1,x1x2=t-3,
∵点D是线段B'C'的三等分点,∴x2=-3x1或x1=-3x2;
当x2=3x1时,x1-3x1=1,求出t=,D点坐标为(0,);
当x1=-3x2时;-3x2+x2=1,∴x2=-(不符合题意,舍去),∴D(0,)
核心考点8 二次函数与最值
方法归納8 设参数→几何性质→二次函数→最值
8.如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,直线y=x+1过点A,交抛物线于另一点D.在AD上方抛物线上有一点F,过点F作FG⊥AD于G,作FH∥x轴交直线AD于H,求△FGH的周长的最大值
解:思路一:∠DAB=45°,△FGH为等腰直角三角形,FG: HG: FH=1:1:2,
设F(m,-m2+m+3),把y=-m2+2m+3
代入y=x+1,xH=-m2+2m+2,FH=-m2+2m+2-m=-m2+m+2,
C△FGH=FH+FG+HG=(+1)FH=-(+1)(m-)2+,
当m=时,△FGH周长的最大值为.
思路二:将直线AD向上平移至与抛物线只有一个公共F时,FG最大,故△FGH周长最大,再用判别式△=0求解.
核心考点9 二次函数与定值
方法归纳9 设参→几何性质→代数式→消参→定值
9.如图,点P为抛物线y=-x2+8在第一象限部分上一动点,y轴上有一点B(0,6),PC⊥x轴于C,试判断:PB+PC的值是否为定值?说明理由.
解;过点P作PQ⊥y轴于Q.设P(x,x2+8),
则PQ=x,PC=x2+8,PB=x2+2,PB+PC=10,故PB+PC的值为定值.
核心考点10 二次函数与定点和定直线
方法归纳10 配方(分解因式)→定点→定直线
10.(1)证明:无论m为何实数,二次函数y=x2-(2-m)x+m的图象总是经过一定点.
(2)证明无论a取任何实数,抛物线y=x2+(a+1)x+a2-的顶点都在一条定直线上.
证明:(1)可证x=-1时,y=3,故图早过定点(-1,3)
(2)可得项点(-,-),故顶点在直线y=x上.
核心考点11 二次函数与公共点
方法归纳11 画图象一设参一联立消y→判别式→求范围
11.若直线y=2x+t与函数y=的图象有且只有两个公共点时,则t的取值范围是t=-3或t>-2
解:如图,图象与x交于A(1,0),B(-3,0),与y轴交于C(0,-3),
①当直线y=2x+t过点A(1,0)时,t=-2,此时图象与直y=2x+t有3个公点,
②由得:x2-4x+1-t=0,△=16-4(1-t)=0,t=-3,由得:x2-3-t=0,△=0-4(-3-t)=0.t=-3,当t=-3时,图象与直线y=2x+t只有两个公共点:
综上所述,t的取值范围是t=-3或t>-2
方法归纳12 特征点→不等式(组)→求范国
12.已知关于x的方程y=ax2-(a2-2)x-2a的图象与x轴的一个交点为(m,0).若-2<m<-1.求a的取值范围.
解:今y=0,得-(a2-2)x-2a=0,得x1=a,x2=,
①当a>0时,-2<<-1,得1<a<2,
②当a<0时,-2<a<-1.
综上a的范围为1<a<2或-2<a<-1
21世纪教育网(www.21cnjy.com)
同课章节目录
