第二十二章 二次函数单元检测题(含答案)
文档属性
| 名称 | 第二十二章 二次函数单元检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 10:34:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
9.九年级数学(上)第22章《二次函数》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟满分120分)
―、选择题(每小题3分,共30分)
1.拋物线y=2(x+3)2-1的顶点坐标是( )
A.(3,1) B.(3,-1) C.(-3,1) D.(-3,-1)
2.抛物线与y=ax2的形状相同,而开口方向相反, 则a的值是( )
A. B.3 C.-3 D.
3. 二次函数:y=x2+4x+5的图象的对称轴为( )
A.x=4 B.x=-4 C.x=2 D.x=—2
4.在二次函数y=x2+2x+1的图象上,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
5.把二次函数y=x2+2x-1配方成顶点式为( )
A.y=(x-1)2 B.y=(x—1)2-2
C.y=(x+1)2+1 D.y=(x+1)2-2
6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.图象的对称轴是直线
C.当x<,随x的增大而增大 D.当一1<x<2 时,y<0
第6题图 第9题图
7.二次函数y=kx2-6x+3的图象与x轴有两个不同的交点,则k的取值范围是( )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
8.把拋物线y=(x-1)2+3绕原点旋转180°后得到的拋物线为( )
A.y=-(x-1)2+3 B.y=-(x+1)2+3
C. y=-(x+1)2-3 D.y=-(x-1)2-3
9. 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC的时间是( )
A.36秒 B.42秒 C.38秒 D.44秒
10.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx-t=0 (t为实数)在一1<x<4的范围内有解,则t的取值范围是( )
A. t<8 B.t<3 C.-1≤t<8 D. —1≤t<3
二、填空题(每小题3分,共18分)
11.拋物线y=-x2+10有最 点(填“高”或“低”),其坐标是 .
12.若拋物线y=x2-2x-3与x轴分别交于A,B两点,A,B两点的坐标分别是 和 .
13.已知拋物线y=x2-(m-4)x+2m-3的对称轴是x=-2,则m的值为 .
14.若拋物线y=x2-6x+c的顶点与原点的距离为5,则c的值为 .
15.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:s=v0t-gt2(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面 m.
16. 当x≤3时,函数y=x2-2x-3的图象记为G,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M,若直线y=x+b与图象M有且只有两个公共点,则b的取值范围是 .
三、解答题(共8题,共72分)
17.(本题8分)已知二次函数y=2x2-4x.
(1) 求它的开口方向、对称轴和顶点坐标;
(2) 判断点A(-1,6)是否在此二次函数的图象上?
18.(本题8分)已知拋物线经过点(2,3),且顶点坐标为(1,1),求这条拋物线的解析式.
19.(本题8分)如图,已知拋物线:y=x2+bx+c经过A(-1,0)、B(3,0) 两点.
(1) 求拋物线的解析式和顶点坐标;
(2) 当0<x<3时,求y的取值范围.
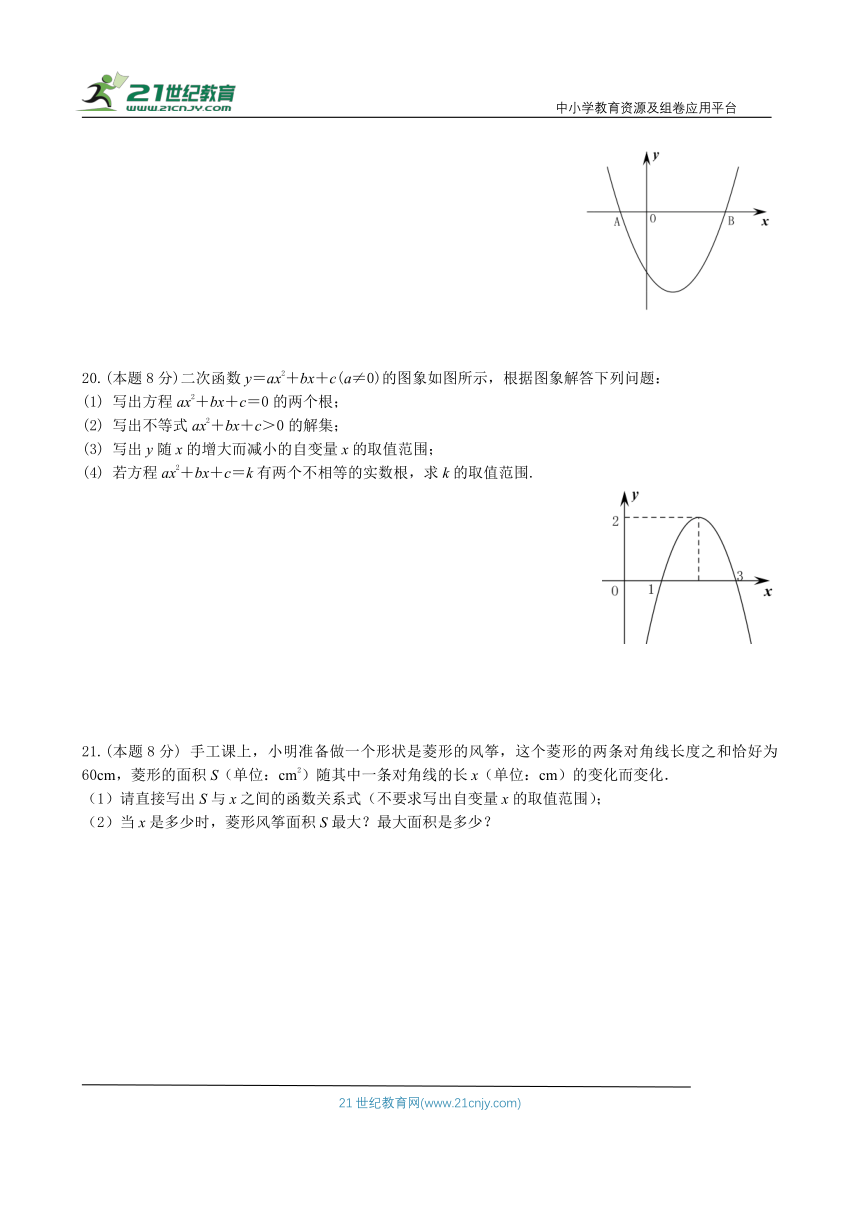
20.(本题8分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1) 写出方程ax2+bx+c=0的两个根;
(2) 写出不等式ax2+bx+c>0的解集;
(3) 写出y随x的增大而减小的自变量x的取值范围;
(4) 若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
21.(本题8分) 手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?
22.(本题10分)已知二次函数y=-x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求的值.
23.(本题10分) 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
24.(本小题12分)已知拋物线y=-x2+bx+c与x轴交于A,B两点与y轴交于C点.
(1) 当B与A重合,且OC=2OA时,
① 求拋物线的解析式;
② 如图1,F为拋物线上一点,FE丄x轴于点E,P是线段FE上一点,PA交拋物线于点M,MN丄EF于点N.当MN=OA时, 求PF—PN的值;
(2) 如图2,过A作x轴的垂线交于点P,当AB=3时,求直线OP的解析式.
9.九年级数学(上)第22章《二次函数》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟满分120分)
―、选择题(每小题3分,共30分)
1.拋物线y=2(x+3)2-1的顶点坐标是( D )
A.(3,1) B.(3,-1) C.(-3,1) D.(-3,-1)
2.抛物线与y=ax2的形状相同,而开口方向相反, 则a的值是( D )
A. B.3 C.-3 D.
3. 二次函数:y=x2+4x+5的图象的对称轴为( D )
A.x=4 B.x=—4 C.x=2 D.x=—2
4.在二次函数y=x2+2x+1的图象上,若y随x的增大而增大,则x的取值范围是( D )
A.x<1 B.x>1 C.x<-1 D.x>-1
5.把二次函数y=x2+2x-1配方成顶点式为( D )
A.y=(x-1)2 B.y=(x—1)2-2
C.y=(x+1)2+1 D.y=(x+1)2-2
6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( C )
A.函数有最小值 B.图象的对称轴是直线
C.当x<,随x的增大而增大 D.当一1<x<2 时,y<0
7.二次函数y=kx2-6x+3的图象与x轴有两个不同的交点,则k的取值范围是( B )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
8.把拋物线y=(x-1)2+3绕原点旋转180°后得到的拋物线为( C )
A.y=-(x-1)2+3 B.y=-(x+1)2+3
C. y=-(x+1)2-3 D.y=-(x-1)2-3
9. 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC的时间是( A )
A.36秒 B.42秒 C.38秒 D.44秒
10.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx-t=0 (t为实数)在一1<x<4的范围内有解,则t的取值范围是( C )
A. t<8 B.t<3 C.-1≤t<8 D. —1≤t<3
二、填空题(每小题3分,共18分)
11.拋物线y=-x2+10有最 高 点(填“高”或“低”),其坐标是 (0,10) .
12.若拋物线y=x2-2x-3与x轴分别交于A,B两点,A,B两点的坐标分别是(3,0 )和(-1,0 ).
13.已知拋物线y=x2-(m-4)x+2m-3的对称轴是x=-2,则m的值为 0 .
14.若拋物线y=x2-6x+c的顶点与原点的距离为5,则c的值为 5或13 .
15.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:s=v0t-gt2(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面 7 m.
16. 当x≤3时,函数y=x2-2x-3的图象记为G,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M,若直线y=x+b与图象M有且只有两个公共点,则b的取值范围是 b=或-3<<1 .
解:∵y=x2-2x-3,当y=0,则0=x2-2x-3,
解得:x1=-1,x2=3,
当直线y=x+b过(-1,0)时,b=1,
当直线y=x+b过(3,0)时,b=-3,
故当-3<b<1时,直线y=x+b与图象M有且只有两个公共点,
当直线y=x+b与抛物线y=x2-2x-3有一个交点,
则x2-3x-3-b=0有两个相等的实数根,
故△=b2-4ac=21+4b=0,
解得:b=,
综上所述:直线y=x+b与图象M有且只有两个公共点,则b的取值范是:-3<b<1或b=.
三、解答题(共8题,共72分)
17.(本题8分)已知二次函数y=2x2-4x.
(1) 求它的开口方向、对称轴和顶点坐标;
(2) 判断点A(-1,6)是否在此二次函数的图象上?
解:(1) ∵y=2x2-4x=2(x-1)2-2,
∴对称轴为直线x=1,顶点坐标为(1,-2).
(2)点A(-1,6)在此二次函数的图象上.
18.(本题8分)已知拋物线经过点(2,3),且顶点坐标为(1,1),求这条拋物线的解析式.
解:∵顶点坐标为(1,1),∴设抛物线为y=a(x-1)2+1,
∵抛物线经过点(2,3),
∴3=a(2-1)2+1,解得a=2.
∴y=2(x-1)2+1=2x2-4x+3.
19.(本题8分)如图,已知拋物线:y=x2+bx+c经过A(-1,0)、B(3,0) 两点.
(1) 求拋物线的解析式和顶点坐标;
(2) 当0<x<3时,求y的取值范围.
解:⑴抛物线的解析式为y=x2-2x-3.顶点坐标为(1,-4);
(2)由图可得当0<x<3时,-4≤y<0.
20.(本题8分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1) 写出方程ax2+bx+c=0的两个根;
(2) 写出不等式ax2+bx+c>0的解集;
(3) 写出y随x的增大而减小的自变量x的取值范围;
(4) 若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
解:x1=1,x2=3;
(2)1<x<3;
(3)x>2;
⑷k<2.
21.(本题8分) 手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?
解:(1)S=;
(2)∵S=,且<0,
∴当 x=30时,S有最大值,最大值为450.
即当为30cm时,菱形风筝的面积最大,最大 面积是450cm2.
22.(本题10分)已知二次函数y=-x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求的值.
解:解:(1)∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0,∴m>﹣1;
(2)∵二次函数的图象过点A(3,0),
∴0=﹣9+6+m,∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,∴B(0,3),
∴直线AB的解析式为y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).∴BP=,AP=,∴.
23.(本题10分) 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
解:(1)设y与x满足的函数关系式为:y=kx+b.
由题意可得:,解得,
故y与x的函数关系式为:y=-3x+108.
(2)每天获得的利润为:
P=(-3x+108)(x-20)=-3x2+168x-2160=-3(x-28)2+192.
故当销售价定为28元时,每天获得的利润最大.
24.(本小题12分)已知拋物线y=-x2+bx+c与x轴交于A,B两点与y轴交于C点.
(1) 当B与A重合,且OC=2OA时,
① 求拋物线的解析式;
② 如图1,F为拋物线上一点,FE丄x轴于点E,P是线段FE上一点,PA交拋物线于点M,MN丄EF于点N.当MN=OA时, 求PF—PN的值;
(2) 如图2,过A作x轴的垂线交于点P,当AB=3时,求直线OP的解析式.
解:⑴①=b2+4c=0,∴c=b2,
∴y=-x2+bxb2=,
∴OA=,OC=2OA=b,∴b2=b,又b≠0,
∴b=4,c=-4,∴y=-x2+4x-4.
②设AP的解析式为y=k(x-2),∴,可求xM=2-k,∴yM=-k2,
又MN=OA=1,∴N(3-k,-k2),F(3-k,-(1-k)2),P(3-k,k(1-k),
∴PF=yP-yF=k(1-k)+(1-k)2=1-k,
PN=yN-yP=-k2-k(1-k)=-k,∴PF-PN=1-k-(-k)=1.
⑵设BC的解析式为y=kx+c,A(a,0),B(t,0),则kt+c=0,∴k=,∴y=x+c,
当x=a时,y=+c.
∴P(a, +c),设OP的解析式为y=mx,得+c=ma,∴mat=-ac+tc=c(t-a),
∴m=,又含y=-x2+bx+c=0,则xAxB=at=-c,AB=t-a=3,
∴m=-3,∴OP的解析式为y=-3x.
21世纪教育网(www.21cnjy.com)
9.九年级数学(上)第22章《二次函数》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟满分120分)
―、选择题(每小题3分,共30分)
1.拋物线y=2(x+3)2-1的顶点坐标是( )
A.(3,1) B.(3,-1) C.(-3,1) D.(-3,-1)
2.抛物线与y=ax2的形状相同,而开口方向相反, 则a的值是( )
A. B.3 C.-3 D.
3. 二次函数:y=x2+4x+5的图象的对称轴为( )
A.x=4 B.x=-4 C.x=2 D.x=—2
4.在二次函数y=x2+2x+1的图象上,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
5.把二次函数y=x2+2x-1配方成顶点式为( )
A.y=(x-1)2 B.y=(x—1)2-2
C.y=(x+1)2+1 D.y=(x+1)2-2
6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.图象的对称轴是直线
C.当x<,随x的增大而增大 D.当一1<x<2 时,y<0
第6题图 第9题图
7.二次函数y=kx2-6x+3的图象与x轴有两个不同的交点,则k的取值范围是( )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
8.把拋物线y=(x-1)2+3绕原点旋转180°后得到的拋物线为( )
A.y=-(x-1)2+3 B.y=-(x+1)2+3
C. y=-(x+1)2-3 D.y=-(x-1)2-3
9. 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC的时间是( )
A.36秒 B.42秒 C.38秒 D.44秒
10.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx-t=0 (t为实数)在一1<x<4的范围内有解,则t的取值范围是( )
A. t<8 B.t<3 C.-1≤t<8 D. —1≤t<3
二、填空题(每小题3分,共18分)
11.拋物线y=-x2+10有最 点(填“高”或“低”),其坐标是 .
12.若拋物线y=x2-2x-3与x轴分别交于A,B两点,A,B两点的坐标分别是 和 .
13.已知拋物线y=x2-(m-4)x+2m-3的对称轴是x=-2,则m的值为 .
14.若拋物线y=x2-6x+c的顶点与原点的距离为5,则c的值为 .
15.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:s=v0t-gt2(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面 m.
16. 当x≤3时,函数y=x2-2x-3的图象记为G,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M,若直线y=x+b与图象M有且只有两个公共点,则b的取值范围是 .
三、解答题(共8题,共72分)
17.(本题8分)已知二次函数y=2x2-4x.
(1) 求它的开口方向、对称轴和顶点坐标;
(2) 判断点A(-1,6)是否在此二次函数的图象上?
18.(本题8分)已知拋物线经过点(2,3),且顶点坐标为(1,1),求这条拋物线的解析式.
19.(本题8分)如图,已知拋物线:y=x2+bx+c经过A(-1,0)、B(3,0) 两点.
(1) 求拋物线的解析式和顶点坐标;
(2) 当0<x<3时,求y的取值范围.
20.(本题8分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1) 写出方程ax2+bx+c=0的两个根;
(2) 写出不等式ax2+bx+c>0的解集;
(3) 写出y随x的增大而减小的自变量x的取值范围;
(4) 若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
21.(本题8分) 手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?
22.(本题10分)已知二次函数y=-x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求的值.
23.(本题10分) 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
24.(本小题12分)已知拋物线y=-x2+bx+c与x轴交于A,B两点与y轴交于C点.
(1) 当B与A重合,且OC=2OA时,
① 求拋物线的解析式;
② 如图1,F为拋物线上一点,FE丄x轴于点E,P是线段FE上一点,PA交拋物线于点M,MN丄EF于点N.当MN=OA时, 求PF—PN的值;
(2) 如图2,过A作x轴的垂线交于点P,当AB=3时,求直线OP的解析式.
9.九年级数学(上)第22章《二次函数》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟满分120分)
―、选择题(每小题3分,共30分)
1.拋物线y=2(x+3)2-1的顶点坐标是( D )
A.(3,1) B.(3,-1) C.(-3,1) D.(-3,-1)
2.抛物线与y=ax2的形状相同,而开口方向相反, 则a的值是( D )
A. B.3 C.-3 D.
3. 二次函数:y=x2+4x+5的图象的对称轴为( D )
A.x=4 B.x=—4 C.x=2 D.x=—2
4.在二次函数y=x2+2x+1的图象上,若y随x的增大而增大,则x的取值范围是( D )
A.x<1 B.x>1 C.x<-1 D.x>-1
5.把二次函数y=x2+2x-1配方成顶点式为( D )
A.y=(x-1)2 B.y=(x—1)2-2
C.y=(x+1)2+1 D.y=(x+1)2-2
6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( C )
A.函数有最小值 B.图象的对称轴是直线
C.当x<,随x的增大而增大 D.当一1<x<2 时,y<0
7.二次函数y=kx2-6x+3的图象与x轴有两个不同的交点,则k的取值范围是( B )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
8.把拋物线y=(x-1)2+3绕原点旋转180°后得到的拋物线为( C )
A.y=-(x-1)2+3 B.y=-(x+1)2+3
C. y=-(x+1)2-3 D.y=-(x-1)2-3
9. 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC的时间是( A )
A.36秒 B.42秒 C.38秒 D.44秒
10.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx-t=0 (t为实数)在一1<x<4的范围内有解,则t的取值范围是( C )
A. t<8 B.t<3 C.-1≤t<8 D. —1≤t<3
二、填空题(每小题3分,共18分)
11.拋物线y=-x2+10有最 高 点(填“高”或“低”),其坐标是 (0,10) .
12.若拋物线y=x2-2x-3与x轴分别交于A,B两点,A,B两点的坐标分别是(3,0 )和(-1,0 ).
13.已知拋物线y=x2-(m-4)x+2m-3的对称轴是x=-2,则m的值为 0 .
14.若拋物线y=x2-6x+c的顶点与原点的距离为5,则c的值为 5或13 .
15.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:s=v0t-gt2(其中g是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面 7 m.
16. 当x≤3时,函数y=x2-2x-3的图象记为G,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M,若直线y=x+b与图象M有且只有两个公共点,则b的取值范围是 b=或-3<<1 .
解:∵y=x2-2x-3,当y=0,则0=x2-2x-3,
解得:x1=-1,x2=3,
当直线y=x+b过(-1,0)时,b=1,
当直线y=x+b过(3,0)时,b=-3,
故当-3<b<1时,直线y=x+b与图象M有且只有两个公共点,
当直线y=x+b与抛物线y=x2-2x-3有一个交点,
则x2-3x-3-b=0有两个相等的实数根,
故△=b2-4ac=21+4b=0,
解得:b=,
综上所述:直线y=x+b与图象M有且只有两个公共点,则b的取值范是:-3<b<1或b=.
三、解答题(共8题,共72分)
17.(本题8分)已知二次函数y=2x2-4x.
(1) 求它的开口方向、对称轴和顶点坐标;
(2) 判断点A(-1,6)是否在此二次函数的图象上?
解:(1) ∵y=2x2-4x=2(x-1)2-2,
∴对称轴为直线x=1,顶点坐标为(1,-2).
(2)点A(-1,6)在此二次函数的图象上.
18.(本题8分)已知拋物线经过点(2,3),且顶点坐标为(1,1),求这条拋物线的解析式.
解:∵顶点坐标为(1,1),∴设抛物线为y=a(x-1)2+1,
∵抛物线经过点(2,3),
∴3=a(2-1)2+1,解得a=2.
∴y=2(x-1)2+1=2x2-4x+3.
19.(本题8分)如图,已知拋物线:y=x2+bx+c经过A(-1,0)、B(3,0) 两点.
(1) 求拋物线的解析式和顶点坐标;
(2) 当0<x<3时,求y的取值范围.
解:⑴抛物线的解析式为y=x2-2x-3.顶点坐标为(1,-4);
(2)由图可得当0<x<3时,-4≤y<0.
20.(本题8分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1) 写出方程ax2+bx+c=0的两个根;
(2) 写出不等式ax2+bx+c>0的解集;
(3) 写出y随x的增大而减小的自变量x的取值范围;
(4) 若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
解:x1=1,x2=3;
(2)1<x<3;
(3)x>2;
⑷k<2.
21.(本题8分) 手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?
解:(1)S=;
(2)∵S=,且<0,
∴当 x=30时,S有最大值,最大值为450.
即当为30cm时,菱形风筝的面积最大,最大 面积是450cm2.
22.(本题10分)已知二次函数y=-x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求的值.
解:解:(1)∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0,∴m>﹣1;
(2)∵二次函数的图象过点A(3,0),
∴0=﹣9+6+m,∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,∴B(0,3),
∴直线AB的解析式为y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).∴BP=,AP=,∴.
23.(本题10分) 在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
解:(1)设y与x满足的函数关系式为:y=kx+b.
由题意可得:,解得,
故y与x的函数关系式为:y=-3x+108.
(2)每天获得的利润为:
P=(-3x+108)(x-20)=-3x2+168x-2160=-3(x-28)2+192.
故当销售价定为28元时,每天获得的利润最大.
24.(本小题12分)已知拋物线y=-x2+bx+c与x轴交于A,B两点与y轴交于C点.
(1) 当B与A重合,且OC=2OA时,
① 求拋物线的解析式;
② 如图1,F为拋物线上一点,FE丄x轴于点E,P是线段FE上一点,PA交拋物线于点M,MN丄EF于点N.当MN=OA时, 求PF—PN的值;
(2) 如图2,过A作x轴的垂线交于点P,当AB=3时,求直线OP的解析式.
解:⑴①=b2+4c=0,∴c=b2,
∴y=-x2+bxb2=,
∴OA=,OC=2OA=b,∴b2=b,又b≠0,
∴b=4,c=-4,∴y=-x2+4x-4.
②设AP的解析式为y=k(x-2),∴,可求xM=2-k,∴yM=-k2,
又MN=OA=1,∴N(3-k,-k2),F(3-k,-(1-k)2),P(3-k,k(1-k),
∴PF=yP-yF=k(1-k)+(1-k)2=1-k,
PN=yN-yP=-k2-k(1-k)=-k,∴PF-PN=1-k-(-k)=1.
⑵设BC的解析式为y=kx+c,A(a,0),B(t,0),则kt+c=0,∴k=,∴y=x+c,
当x=a时,y=+c.
∴P(a, +c),设OP的解析式为y=mx,得+c=ma,∴mat=-ac+tc=c(t-a),
∴m=,又含y=-x2+bx+c=0,则xAxB=at=-c,AB=t-a=3,
∴m=-3,∴OP的解析式为y=-3x.
21世纪教育网(www.21cnjy.com)
同课章节目录
