数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 578.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 17:33:12 | ||
图片预览






文档简介
(共18张PPT)
1.1.2 空间向量的数量积运算
1.了解空间向量夹角的概念及表示方法.
2.掌握空间向量数量积的计算方法及应用.(重点)
3.能将立体几何问题转化为向量运算问题.(难点)
学习目标
O
A
B
∠AOB
[0,π]
1.空间向量夹角
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积都等于零.
2.空间两个向量的数量积
注:性质①是证明两向量垂直的依据; 性质②是求向量的长度(模)的依据.
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b = ______;若反向,则a·b = ________.
特别地,a·a =____或 |a| =
③若θ为a,b的夹角,则cos θ=_______
④|a·b| ≤ |a|·|b|
a·b=0
|a|·|b|
-|a|·|b|
|a|2
两个向量数量积的性质
如图所示,在空间四边形OABC中,OA=8,AB=6,AC=4,
BC=5,∠OAC=45°,∠OAB=60°,求OA与BC夹角的余弦值.
例题
D
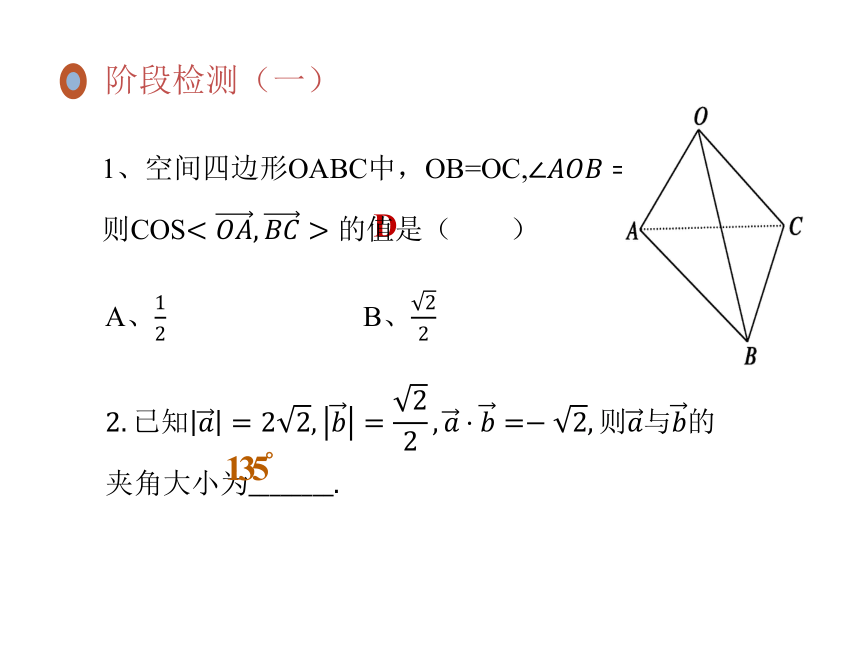
阶段检测(一)
1、空间四边形OABC中,OB=OC,=,
则COS值是( )
A、 B、 C、 - D、 0
D
A. 12 B.8
C.4 D.13
阶段检测(一)
(2)
(1)
如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c = |a|cos,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线 l 投影 (图1.1-11 (2))
空间向量的投影
如图1.1-11(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量,向量称为向量a在平面β上的投影向量.这时,向量a,的夹角就是向量a所在直线与平面β所成的角.
(3)
注:向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立.
空间向量的运算律
在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
例1
已知:如图,PO,PA分别是平面的垂线、斜线,AO是PA在平面内的射影,,且.
求证:.
在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.
逆命题成立吗
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
m
n
g
取已知平面内的任一条直线g,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件 要证的目标可以转化为向量的什么目标 怎样建立向量的条件与向量的目标的联系
例2
m
n
g
以上命题中的真命题是 ( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(2)(4)
阶段检测(二)
___________
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1.证明两直线垂直.
2.求两点之间的距离或线段长度.
3.证明线面垂直.
4.求两直线所成角的余弦值等.
课堂小结
1.1.2 空间向量的数量积运算
1.了解空间向量夹角的概念及表示方法.
2.掌握空间向量数量积的计算方法及应用.(重点)
3.能将立体几何问题转化为向量运算问题.(难点)
学习目标
O
A
B
∠AOB
[0,π]
1.空间向量夹角
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积都等于零.
2.空间两个向量的数量积
注:性质①是证明两向量垂直的依据; 性质②是求向量的长度(模)的依据.
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b = ______;若反向,则a·b = ________.
特别地,a·a =____或 |a| =
③若θ为a,b的夹角,则cos θ=_______
④|a·b| ≤ |a|·|b|
a·b=0
|a|·|b|
-|a|·|b|
|a|2
两个向量数量积的性质
如图所示,在空间四边形OABC中,OA=8,AB=6,AC=4,
BC=5,∠OAC=45°,∠OAB=60°,求OA与BC夹角的余弦值.
例题
D
阶段检测(一)
1、空间四边形OABC中,OB=OC,=,
则COS值是( )
A、 B、 C、 - D、 0
D
A. 12 B.8
C.4 D.13
阶段检测(一)
(2)
(1)
如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c = |a|cos
空间向量的投影
如图1.1-11(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量,向量称为向量a在平面β上的投影向量.这时,向量a,的夹角就是向量a所在直线与平面β所成的角.
(3)
注:向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立.
空间向量的运算律
在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
例1
已知:如图,PO,PA分别是平面的垂线、斜线,AO是PA在平面内的射影,,且.
求证:.
在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.
逆命题成立吗
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
m
n
g
取已知平面内的任一条直线g,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件 要证的目标可以转化为向量的什么目标 怎样建立向量的条件与向量的目标的联系
例2
m
n
g
以上命题中的真命题是 ( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(2)(4)
阶段检测(二)
___________
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1.证明两直线垂直.
2.求两点之间的距离或线段长度.
3.证明线面垂直.
4.求两直线所成角的余弦值等.
课堂小结
