§26.2 求二次函数的函数关系式(广东省惠州市惠东县)
文档属性
| 名称 | §26.2 求二次函数的函数关系式(广东省惠州市惠东县) |
|
|
| 格式 | rar | ||
| 文件大小 | 10.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-03 17:26:00 | ||
图片预览


文档简介
§26.2 求二次函数的函数关系式
科任:韦文杰
一、教学目标?
(一)知识与能力?
1.能通过待定系数法求二次函数的关系式.?
2.根据实际问题的不同条件建立相应的二次函数关系式.?
(二)过程与方法?
1.体会实际问题转化为数学模型的过程.?
2.培养学生分析问题、善于思考的能力.?
(三)情感、态度与价值观
体会数学知识与实际生活的紧密联系,体会生活中处处有数学,数学是非常有用的工具.
二、教学重点、难点及教学突破?
(一)教学重点?
用待定系数法求二次函数关系式.?
(二)教学难点?
根据实际问题中的条件,选择适当形式的二次函数关系式.?
(三)教学突破?
教学中注意要引导学生提炼问题式,方便地建立坐标系,从而简化问题的解决.
三、教学过程?
(一)复习引入?
1. 若已知抛物线的顶点为(0,0),则二次函数的关系式可为y=ax (a≠0).
2.若已知抛物线的顶点在y轴上,则二次函数的关系式为y=ax+k(a≠0).
3.若已知抛物线的顶点在x轴上,则二次函数的关系式为y=a(x-h)(a≠0).
4.若已知抛物线的顶点为(h,k),则二次函数的关系式为y=a(x-h)+k(a≠0).?
(二)解决问题,学习新知
1、创设情境,初探教材
(1)阅读分析教材第17页问题2.
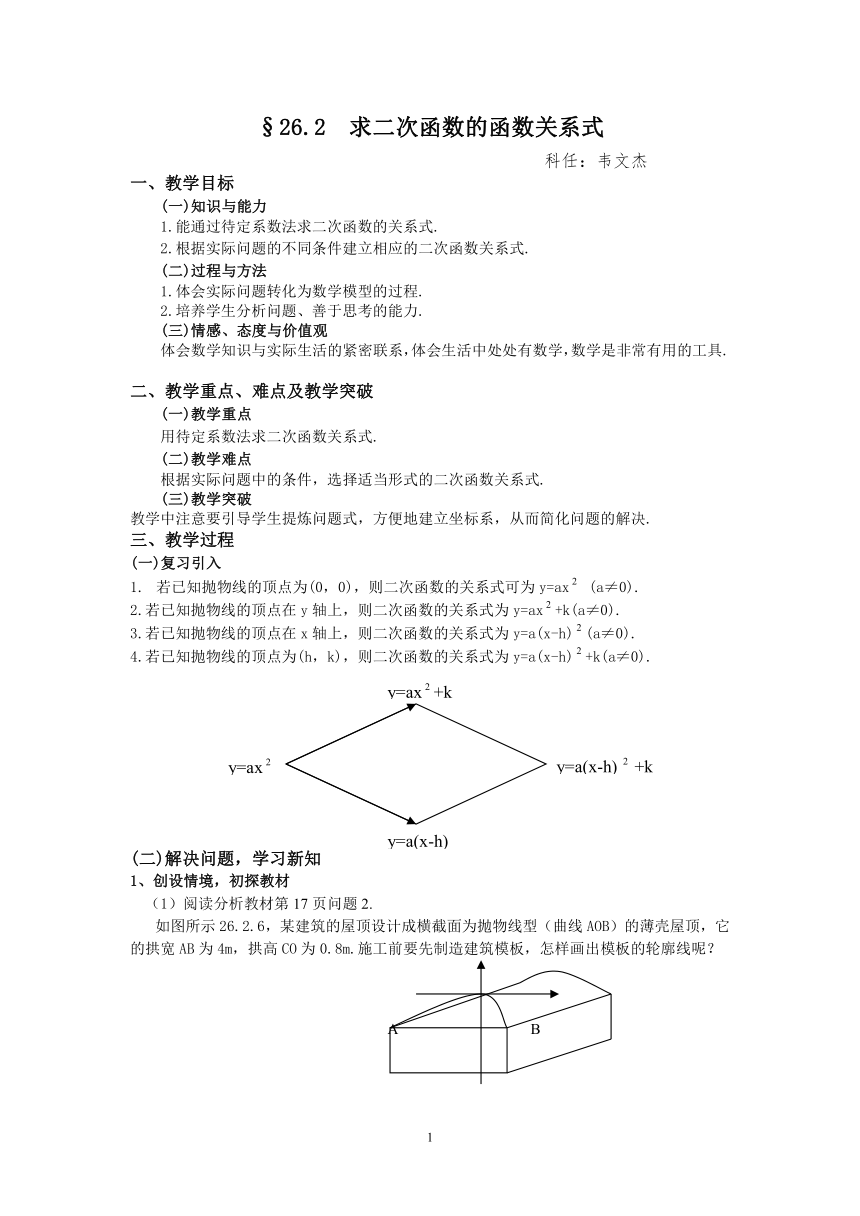
如图所示26.2.6,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶,它的拱宽AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
分析:让学生讨论、交流、分析。通过分析,作出多种建立直角坐标系的方案,并由学生发言,叙述建立各自坐标系的方法及对解决问题的作用.尽量引导学生选择最简单的方案(见教材第17页),并解决问题.
解:
点评:根据建立的直角坐标系,抛物线的顶点在原点,设函数关系式为y= ax(a≠0)
(2)循序渐进,逐步深入
①教材18页例6:已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式。
分析:引导学生分析,由于二次函数过(8,9)是顶点,因此可设函数关系式为y=a(x-8)+9.
解:
点评:当已知抛物线的顶点和抛物线上另一点时,通常设函数关系式为顶点式:y=a(x-h)+k(a≠0)
②教材第18页例7:已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式。
分析:引导学生分析,图象过的三点(0,1)、(2,4)、(3,10),其中有无特殊点 应怎样设函数关系式
解:
点评:当已知抛物线上任意三点时,通常设函数关系式为一般式:y= ax+bx+c(a≠0)
③回顾教材第17页问题2:以AB所在的直线为x轴,以AB的垂直平分线分y轴,建立平面直角坐标系,又可以怎样设函数关系式
分析:如图所示抛物线与x轴的两个交点横坐标为x1 ,x2,即交点A(x1 ,0),交点B(x2,0),
解:
点评:当已知抛物线与x轴的两个交点或交点的横坐标时,通常设函数关系式为交点式:
y=a(x-x1)(x-x2)(a, x1 ,x2为常数,且a≠0)
(3)反馈矫正,突破难点
①二次函数关系式常见有三种形式:
一般式:y=ax+bx+c(a,b,c为常数,且a≠0),关系式的右边是二次三项式,当的一般形式,当已知抛物线上任意三点时,通常设函数关系式为一般式,然后列出a,b,c的三元一次方程组求解,从而求出二次函数的解析式。——(如教材第18页例7)
顶点式:y=a(x-h)+k(a,h,k为常数,且a≠0),由关系式的右边可知,抛物线顶点坐标为(h,k),当已知抛物线的顶点和抛物线上另一点时,通常设函数关系式为顶点式,然后代入另一点的坐标,解关于a的一元一次方程求解,从而求出二次函数的解析式。——(教材18页例6)
交点式(两根式):y=a(x-x1)(x-x2)(a, x1 ,x2为常数,且a≠0),由关系式的右边可知,抛物线与x轴的两个交点横坐标为x1 ,x2,即交点A(x1 ,0),交点B(x2,0),当已知抛物线与x轴的两个交点或交点的横坐标时,通常设函数关系式为交点式,利用第三个条件求解,从而求出二次函数的解析式。——(教材第17页问题2)
②从上述三种关系式可知:要确定二次函数的关系式,必须先确定关系式中的待定系数(常数),而每一种形式中都含有三个待定系数,需要已知三个独立的条件,注重正确地依据相关条件灵活设函数关系式,显得尤为重要。
(三)课堂巩固 基础创关
1、P学案22页知识点一、第5题:已知二次函数y=ax+bx+c经过点M(3,),且经过直线y=3x-6与x轴、y轴的交点A、B,求这个二次函数的关系式。
解:
2、知识点二、第5题:已知抛物线y=ax+bx+c的最高点的坐标为(1,-6),且经过点(2,-8),求此抛物线的解析式。
解:
3、知识点三、第5题:已知抛物线y=ax+bx+c与x轴的两个交点的横坐标为-1、3,与y轴交点的纵坐标为-,求抛物线的解析式。
解:
(四)小结与提高
确定二次函数解析式的主要方法是待定系数法:①当已知抛物线上任意三个点的坐标时,选用一般式较为方便;②当已知抛物线的顶点或对称轴时,选用顶点式较为方便;③当已知抛物线与x轴的两个交点的坐标时,(或横坐标时x1 ,x2)时,选用交点式较为方便。
(五)课后拓展 能力提升
P学案23-25整合训练
(六)作业布置
习题26.2 P课本19页 A类学生做: 第4题:(1)、(2)、(3)
B类学生加做:第5题
(七)下节课主要讲练习:P学案23-25整合训练
(八)课后反思:
y=ax
y=ax+k
y=a(x-h)
y=a(x-h)+k
A
B
PAGE
2
科任:韦文杰
一、教学目标?
(一)知识与能力?
1.能通过待定系数法求二次函数的关系式.?
2.根据实际问题的不同条件建立相应的二次函数关系式.?
(二)过程与方法?
1.体会实际问题转化为数学模型的过程.?
2.培养学生分析问题、善于思考的能力.?
(三)情感、态度与价值观
体会数学知识与实际生活的紧密联系,体会生活中处处有数学,数学是非常有用的工具.
二、教学重点、难点及教学突破?
(一)教学重点?
用待定系数法求二次函数关系式.?
(二)教学难点?
根据实际问题中的条件,选择适当形式的二次函数关系式.?
(三)教学突破?
教学中注意要引导学生提炼问题式,方便地建立坐标系,从而简化问题的解决.
三、教学过程?
(一)复习引入?
1. 若已知抛物线的顶点为(0,0),则二次函数的关系式可为y=ax (a≠0).
2.若已知抛物线的顶点在y轴上,则二次函数的关系式为y=ax+k(a≠0).
3.若已知抛物线的顶点在x轴上,则二次函数的关系式为y=a(x-h)(a≠0).
4.若已知抛物线的顶点为(h,k),则二次函数的关系式为y=a(x-h)+k(a≠0).?
(二)解决问题,学习新知
1、创设情境,初探教材
(1)阅读分析教材第17页问题2.
如图所示26.2.6,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶,它的拱宽AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
分析:让学生讨论、交流、分析。通过分析,作出多种建立直角坐标系的方案,并由学生发言,叙述建立各自坐标系的方法及对解决问题的作用.尽量引导学生选择最简单的方案(见教材第17页),并解决问题.
解:
点评:根据建立的直角坐标系,抛物线的顶点在原点,设函数关系式为y= ax(a≠0)
(2)循序渐进,逐步深入
①教材18页例6:已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式。
分析:引导学生分析,由于二次函数过(8,9)是顶点,因此可设函数关系式为y=a(x-8)+9.
解:
点评:当已知抛物线的顶点和抛物线上另一点时,通常设函数关系式为顶点式:y=a(x-h)+k(a≠0)
②教材第18页例7:已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式。
分析:引导学生分析,图象过的三点(0,1)、(2,4)、(3,10),其中有无特殊点 应怎样设函数关系式
解:
点评:当已知抛物线上任意三点时,通常设函数关系式为一般式:y= ax+bx+c(a≠0)
③回顾教材第17页问题2:以AB所在的直线为x轴,以AB的垂直平分线分y轴,建立平面直角坐标系,又可以怎样设函数关系式
分析:如图所示抛物线与x轴的两个交点横坐标为x1 ,x2,即交点A(x1 ,0),交点B(x2,0),
解:
点评:当已知抛物线与x轴的两个交点或交点的横坐标时,通常设函数关系式为交点式:
y=a(x-x1)(x-x2)(a, x1 ,x2为常数,且a≠0)
(3)反馈矫正,突破难点
①二次函数关系式常见有三种形式:
一般式:y=ax+bx+c(a,b,c为常数,且a≠0),关系式的右边是二次三项式,当的一般形式,当已知抛物线上任意三点时,通常设函数关系式为一般式,然后列出a,b,c的三元一次方程组求解,从而求出二次函数的解析式。——(如教材第18页例7)
顶点式:y=a(x-h)+k(a,h,k为常数,且a≠0),由关系式的右边可知,抛物线顶点坐标为(h,k),当已知抛物线的顶点和抛物线上另一点时,通常设函数关系式为顶点式,然后代入另一点的坐标,解关于a的一元一次方程求解,从而求出二次函数的解析式。——(教材18页例6)
交点式(两根式):y=a(x-x1)(x-x2)(a, x1 ,x2为常数,且a≠0),由关系式的右边可知,抛物线与x轴的两个交点横坐标为x1 ,x2,即交点A(x1 ,0),交点B(x2,0),当已知抛物线与x轴的两个交点或交点的横坐标时,通常设函数关系式为交点式,利用第三个条件求解,从而求出二次函数的解析式。——(教材第17页问题2)
②从上述三种关系式可知:要确定二次函数的关系式,必须先确定关系式中的待定系数(常数),而每一种形式中都含有三个待定系数,需要已知三个独立的条件,注重正确地依据相关条件灵活设函数关系式,显得尤为重要。
(三)课堂巩固 基础创关
1、P学案22页知识点一、第5题:已知二次函数y=ax+bx+c经过点M(3,),且经过直线y=3x-6与x轴、y轴的交点A、B,求这个二次函数的关系式。
解:
2、知识点二、第5题:已知抛物线y=ax+bx+c的最高点的坐标为(1,-6),且经过点(2,-8),求此抛物线的解析式。
解:
3、知识点三、第5题:已知抛物线y=ax+bx+c与x轴的两个交点的横坐标为-1、3,与y轴交点的纵坐标为-,求抛物线的解析式。
解:
(四)小结与提高
确定二次函数解析式的主要方法是待定系数法:①当已知抛物线上任意三个点的坐标时,选用一般式较为方便;②当已知抛物线的顶点或对称轴时,选用顶点式较为方便;③当已知抛物线与x轴的两个交点的坐标时,(或横坐标时x1 ,x2)时,选用交点式较为方便。
(五)课后拓展 能力提升
P学案23-25整合训练
(六)作业布置
习题26.2 P课本19页 A类学生做: 第4题:(1)、(2)、(3)
B类学生加做:第5题
(七)下节课主要讲练习:P学案23-25整合训练
(八)课后反思:
y=ax
y=ax+k
y=a(x-h)
y=a(x-h)+k
A
B
PAGE
2
