12.1 全等三角形 同步练习(含答案)
文档属性
| 名称 | 12.1 全等三角形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 00:00:00 | ||
图片预览

文档简介
12.1 全等三角形
【知识重点】
知识点1 全等形
1. 定义 能够完全重合的两个图形叫做全等形.
全等形的特征 “两相同”与“两无关”.
(1)“两相同”:①形状相同;②大小相同.
(2)“两无关”:①与位置无关;②与方向无关.
2. 全等变换的常见方式 平移、翻折、旋转.
特别解读
●完全重合说明两个图形的周长和面积相等;
●周长或面积相等的两个图形不一定是全等形.
知识点2 全等三角形
1. 全等三角形的相关概念
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形.
(2)全等三角形的对应元素:
①对应顶点:全等三角形中,能够重合的顶点;
②对应边:全等三角形中,能够重合的边;
③对应角:全等三角形中,能够重合的角.
2. 全等三角形的表示方法
全等用符号“≌”表示,读作“全等于”. 记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系,“对边”是指三角形中某个角所对的边,“对角”是指三角形中某条边所对的角.
知识点3 全等三角形的性质
1. 性质 全等三角形的对应边相等,对应角相等.
几何语言:∵△ABC≌△DEF,
∴
2. 拓展 全等三角形的对应元素相等.
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等.
要点提醒
1. 应用全等三角形的性质时,要先确定两个条件:
(1) 两个三角形全等;
(2) 找对应元素.
2. 全等三角形的性质是证明线段、角相等的常用方法.
【经典例题】
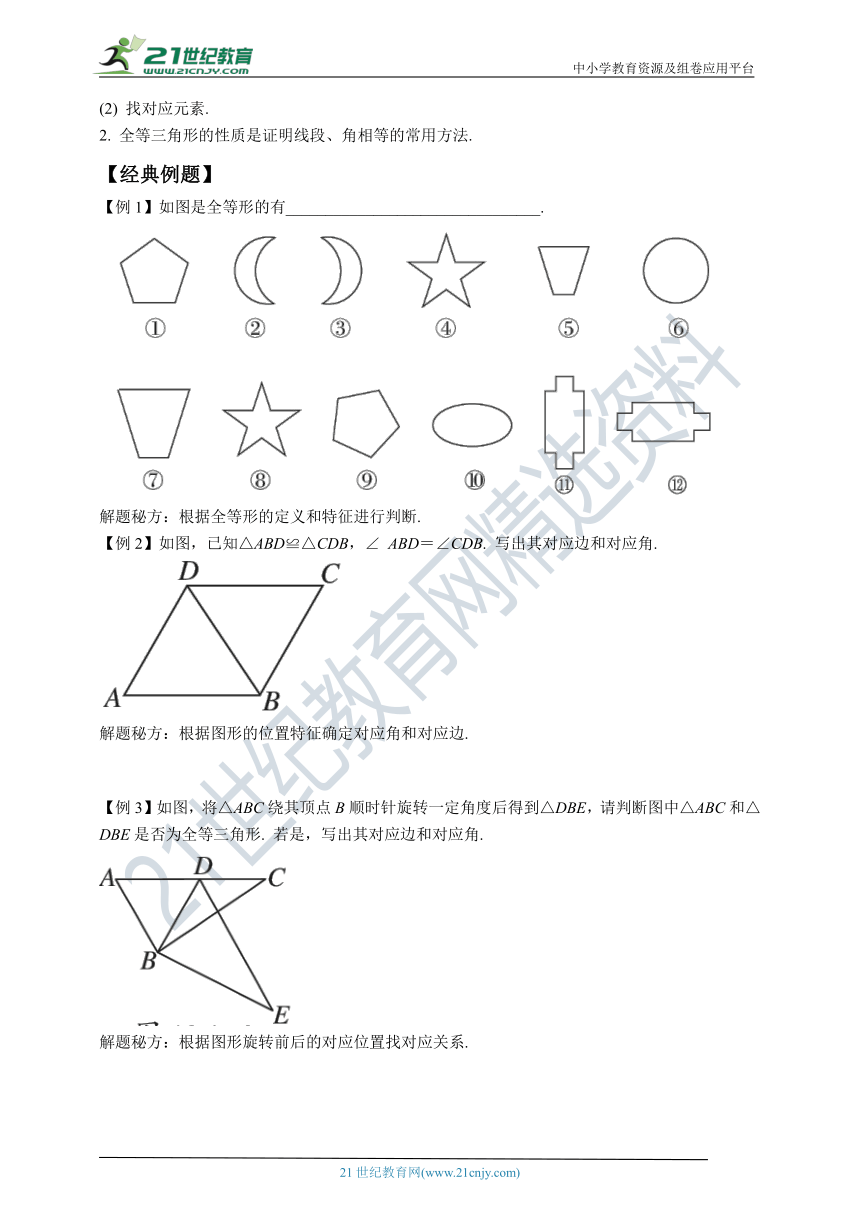
【例1】如图是全等形的有________________________________.
解题秘方:根据全等形的定义和特征进行判断.
【例2】如图,已知△ABD≌△CDB,∠ ABD=∠CDB. 写出其对应边和对应角.
解题秘方:根据图形的位置特征确定对应角和对应边.
【例3】如图,将△ABC绕其顶点B顺时针旋转一定角度后得到△DBE,请判断图中△ABC和△DBE是否为全等三角形. 若是,写出其对应边和对应角.
解题秘方:根据图形旋转前后的对应位置找对应关系.
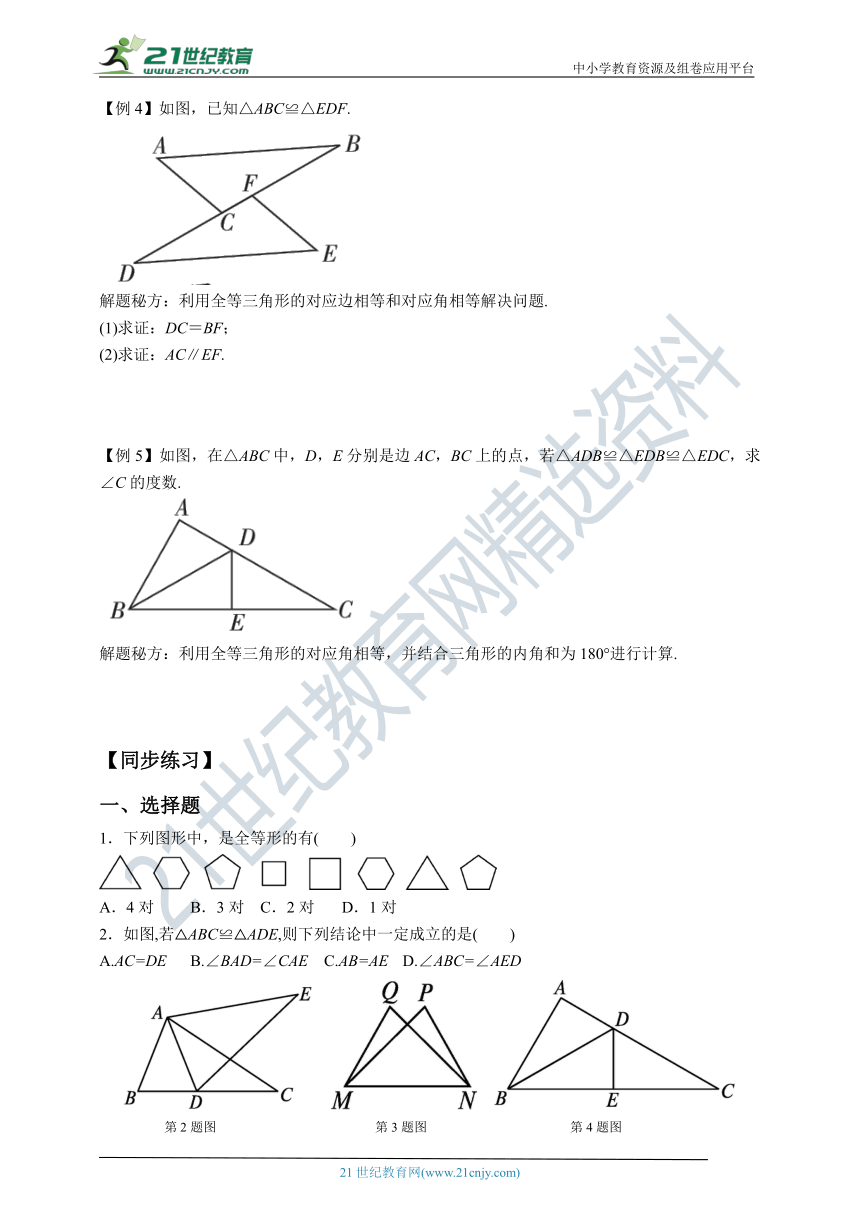
【例4】如图,已知△ABC≌△EDF.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
(1)求证:DC=BF;
(2)求证:AC∥EF.
【例5】如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解题秘方:利用全等三角形的对应角相等,并结合三角形的内角和为180°进行计算.
【同步练习】
一、选择题
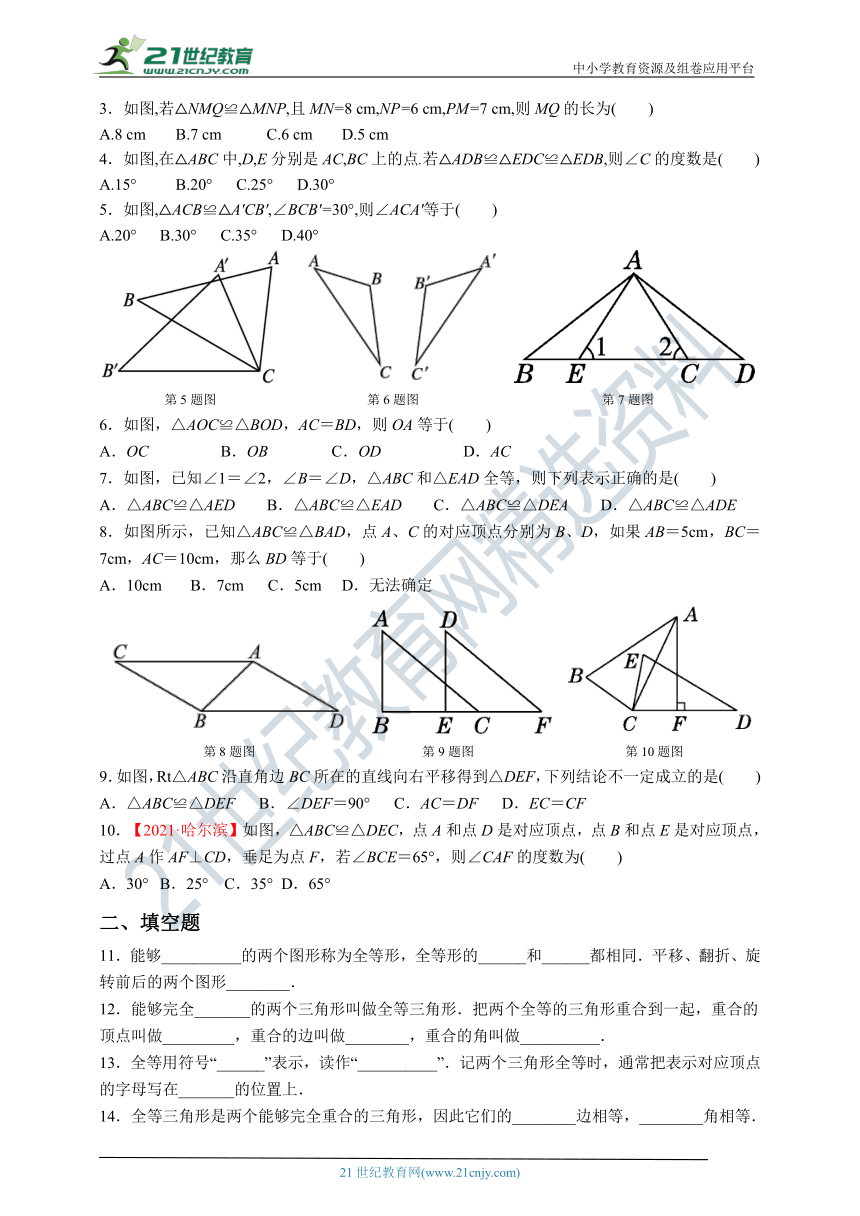
1.下列图形中,是全等形的有( )
A.4对 B.3对 C.2对 D.1对
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
第2题图 第3题图 第4题图
3.如图,若△NMQ≌△MNP,且MN=8 cm,NP=6 cm,PM=7 cm,则MQ的长为( )
A.8 cm B.7 cm C.6 cm D.5 cm
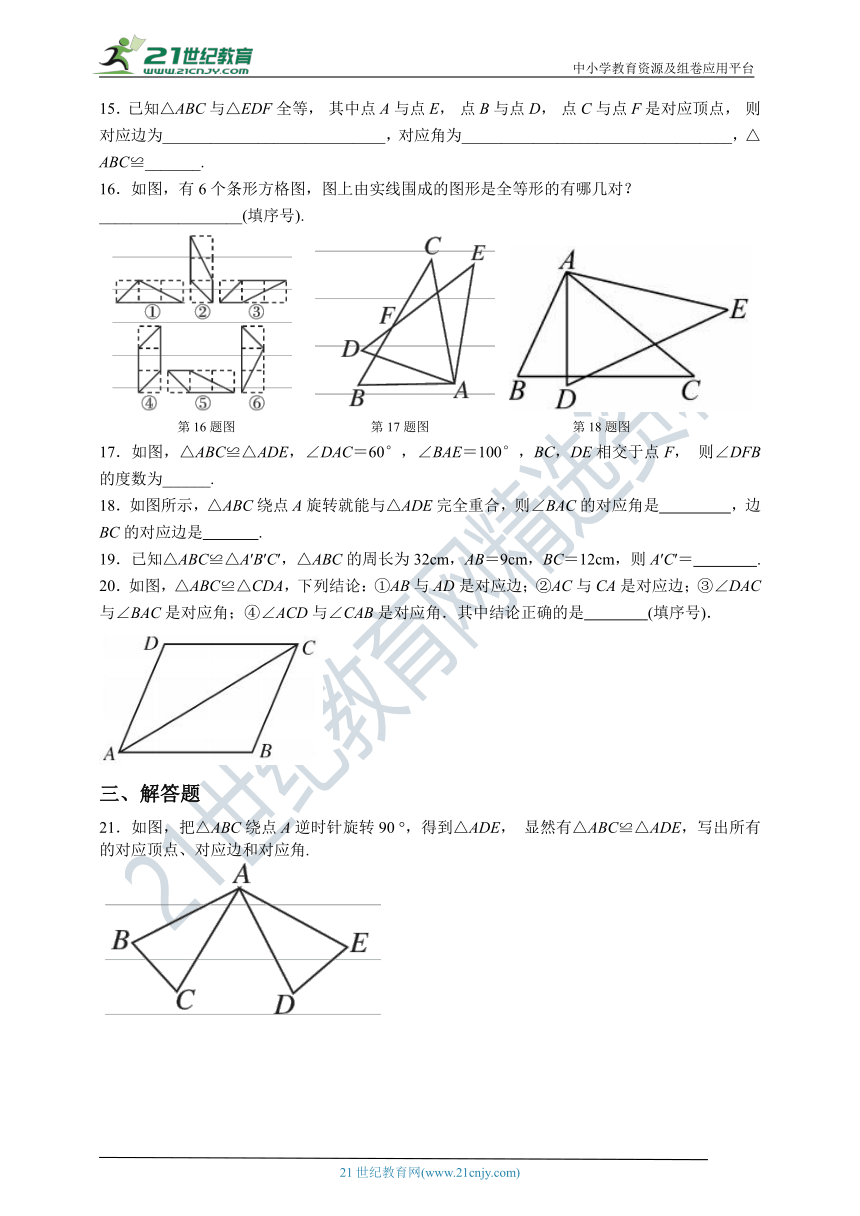
4.如图,在△ABC中,D,E分别是AC,BC上的点.若△ADB≌△EDC≌△EDB,则∠C的度数是( )
A.15° B.20° C.25° D.30°
5.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'等于( )
A.20° B.30° C.35° D.40°
第5题图 第6题图 第7题图
6.如图,△AOC≌△BOD,AC=BD,则OA等于( )
A.OC B.OB C.OD D.AC
7.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列表示正确的是( )
A.△ABC≌△AED B.△ABC≌△EAD C.△ABC≌△DEA D.△ABC≌△ADE
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.10cm B.7cm C.5cm D.无法确定
第8题图 第9题图 第10题图
9.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
10.【2021·哈尔滨】如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
二、填空题
11.能够__________的两个图形称为全等形,全等形的______和______都相同.平移、翻折、旋转前后的两个图形________.
12.能够完全_______的两个三角形叫做全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做_________,重合的边叫做________,重合的角叫做__________.
13.全等用符号“______”表示,读作“__________”.记两个三角形全等时,通常把表示对应顶点的字母写在_______的位置上.
14.全等三角形是两个能够完全重合的三角形,因此它们的________边相等,________角相等.
15.已知△ABC与△EDF全等, 其中点A与点E, 点B与点D, 点C与点F是对应顶点, 则对应边为____________________________,对应角为__________________________________,△ABC≌_______.
16.如图,有6个条形方格图,图上由实线围成的图形是全等形的有哪几对?__________________(填序号).
第16题图 第17题图 第18题图
17.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F, 则∠DFB的度数为______.
18.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
19.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
20.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
三、解答题
21.如图,把△ABC绕点A逆时针旋转90 °,得到△ADE, 显然有△ABC≌△ADE,写出所有的对应顶点、对应边和对应角.
22.如图,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
23.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
24.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2 cm,BC=5 cm.
(1)求DE的长.
(2)DB与AC垂直吗?为什么?
25.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°.
①求∠DBC的度数;
②求∠AFD的度数.
26.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
27.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
(2)若AD=DC=3 cm,BC=4.5 cm,求△DCP与△BPE的周长之和.
28.如图,把两个形状、大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;
(2)判断△AFC的形状.
29.如图,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)求证:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
30.阅读下面的文字,然后回答相关问题:
如图①,若把△ACD沿着直线AC平行移动,它就能和△CBE重合,像这种变换图形位置的方法,叫做平移变换;如图②,若把△ABC沿着直线BC翻折,它就能和△DBC重合,像这种变换图形位置的方法,叫做翻折(或翻转)变换;如图③,若把△AOC绕着点O旋转一定的角度,它将与△EOD重合,像这种变换图形位置的方法,叫做旋转变换.
想一想:(1)如图④,若△ABC≌△DEF,且点B与点E,点C与点F是对应顶点,则进行怎样的图形变换可以使这两个三角形重合
(2)如图⑤,已知△ABF≌△DCE,点E与点F是对应顶点,则△DCE可以看成是由△ABF通过怎样的图形变换得到的
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图是全等形的有________________________________.
【答案】①和⑨、②和③、④和⑧、 和
解题秘方:根据全等形的定义和特征进行判断.
解:上述图形中,⑤和⑦形状相同,但大小不同;⑥和⑩大小、形状都不同. ①和⑨、②和③、 和 尽管方向不同,但大小、形状完全相同,所以它们是全等形;④和⑧都是五角星,大小、形状都相同,是全等形.
确定两个图形全等的方法.
1. 条件判断法:(1) 形状相同;(2) 大小相等,是不是全等形与位置无关.
2. 重合判断法:通过平移、翻折、旋转等方法把两个图形叠合在一起,看它们能否完全重合.
【例2】如图,已知△ABD≌△CDB,∠ ABD=∠CDB. 写出其对应边和对应角.
解题秘方:根据图形的位置特征确定对应角和对应边.
解:BD和DB,AD和CB,AB和CD是对应边;∠A 和∠C,∠ABD和∠CDB,∠ADB和∠CBD是对应角.
方法点拨:利用图形位置关系找对应边和对应角:
①公共角(对顶角)为对应角,公共边为对应边;
②对应角的对边为对应边,两个对应角所夹的边是对应边;
③对应边的对角为对应角,两条对应边所夹的角是对应角.
【例3】如图,将△ABC绕其顶点B顺时针旋转一定角度后得到△DBE,请判断图中△ABC和△DBE是否为全等三角形. 若是,写出其对应边和对应角.
解题秘方:根据图形旋转前后的对应位置找对应关系.
解:△ABC≌△DBE.
AB和DB,AC和DE,BC和BE是对应边;
∠A和∠BDE,∠ABC和∠DBE,∠C和∠E是对应角.
【例4】如图,已知△ABC≌△EDF.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
(1)求证:DC=BF;
证明:∵△ABC≌△EDF,∴ DF=BC.
∴ DF-CF=BC-CF,即DC=BF.
(2)求证:AC∥EF.
∵△ABC≌△EDF,∴∠ACB=∠EFD.
∴ AC∥EF.
【例5】如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解题秘方:利用全等三角形的对应角相等,并结合三角形的内角和为180°进行计算.
解:∵△ADB≌△EDB≌△EDC,
∴∠ABD=∠EBD=∠C,∠A=∠BED=∠CED.
又∵∠BED+∠CED=180°,∴∠BED=∠CED=90°.
∴∠A=90°.
∴∠ABD+∠EBD+∠C=180°-∠A=90°.
∴ 3∠C=90°.∴∠C=30°.
【同步练习】
一、选择题
1.下列图形中,是全等形的有( B )
A.4对 B.3对 C.2对 D.1对
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( B )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
【答案】∵△ABC≌△ADE,∴AB=AD,AC=AE,∠ABC=∠ADE,∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故选B.
第2题图 第3题图 第4题图
3.如图,若△NMQ≌△MNP,且MN=8 cm,NP=6 cm,PM=7 cm,则MQ的长为( C )
A.8 cm B.7 cm C.6 cm D.5 cm
【答案】因为△NMQ≌△MNP,所以MQ与NP是对应边,即MQ=NP=6 cm.
4.如图,在△ABC中,D,E分别是AC,BC上的点.若△ADB≌△EDC≌△EDB,则∠C的度数是( D )
A.15° B.20° C.25° D.30°
【答案】 ∵△EDB≌△EDC,
∴∠DEB=∠DEC=90°.
∵△ADB≌△EDB,
∴∠DAB=∠DEB=90°.
∵△ADB≌△EDB≌△EDC,
∴∠C=∠ABD=∠CBD=30°.
5.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'等于( B )
A.20° B.30° C.35° D.40°
【答案】因为△ACB≌△A'CB',所以∠ACB=∠A'CB',所以∠ACB-∠A'CB=∠A'CB'-∠A'CB,即∠ACA'=∠BCB'=30°.
第5题图 第6题图 第7题图
6.如图,△AOC≌△BOD,AC=BD,则OA等于( B )
A.OC B.OB C.OD D.AC
7.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列表示正确的是( D )
A.△ABC≌△AED B.△ABC≌△EAD C.△ABC≌△DEA D.△ABC≌△ADE
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( A )
A.10cm B.7cm C.5cm D.无法确定
第8题图 第9题图 第10题图
9.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( D )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
10.【2021·哈尔滨】如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( B )
A.30° B.25° C.35° D.65°
二、填空题
11.能够__________的两个图形称为全等形,全等形的______和______都相同.平移、翻折、旋转前后的两个图形________.
【答案】完全重合 形状 大小 全等
12.能够完全_______的两个三角形叫做全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做_________,重合的边叫做________,重合的角叫做__________.
【答案】重合 对应顶点 对应边 对应角
13.全等用符号“______”表示,读作“__________”.记两个三角形全等时,通常把表示对应顶点的字母写在_______的位置上.
【答案】≌ 全等于 对应
14.全等三角形是两个能够完全重合的三角形,因此它们的________边相等,________角相等.
【答案】对应 对应
15.已知△ABC与△EDF全等, 其中点A与点E, 点B与点D, 点C与点F是对应顶点, 则对应边为____________________________,对应角为__________________________________,△ABC≌_______.
【答案】AB与ED,AC与EF,BC与DF
∠A与∠E,∠B与∠D,∠C与∠F
△EDF
16.如图,有6个条形方格图,图上由实线围成的图形是全等形的有哪几对?__________________(填序号).
【答案】①和⑥,②③和⑤
第16题图 第17题图 第18题图
17.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F, 则∠DFB的度数为______.
【答案】20°
18.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
【答案】∠DAE DE
19.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
【答案】11cm
20.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
【答案】②④
三、解答题
21.如图,把△ABC绕点A逆时针旋转90 °,得到△ADE, 显然有△ABC≌△ADE,写出所有的对应顶点、对应边和对应角.
解:对应顶点:A对应A,B对应D,C对应E;
对应边:AB对应AD,AC对应AE,BC对应DE;对应角:∠BAC对应∠DAE,∠B对应∠D,∠C对应∠E.
22.如图,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
解:AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.∴AD⊥BC.
23.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解:∵△EDB≌△EDC,∴∠DEB=∠DEC.
∵∠DEB+∠DEC=180°,∴∠DEB=∠DEC=90°.
∵△ADB≌△EDB≌△EDC,∴∠ADB=∠EDB=∠EDC.
∵∠ADB+∠EDB+∠EDC=180°,
∴∠ADB=∠EDB=∠EDC=60°.
∴∠C=30°.
24.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2 cm,BC=5 cm.
(1)求DE的长.
解:∵△ABD≌△EBC,
∴BD=BC=5 cm,BE=AB=2 cm.
∴DE=BD-BE=3 cm.
(2)DB与AC垂直吗?为什么?
解:DB与AC垂直.理由如下:
∵△ABD≌△EBC,∴∠ABD=∠EBC.
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°.
∴∠EBC=90°,即DB与AC垂直.
25.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°.
①求∠DBC的度数;
②求∠AFD的度数.
解:(1)3;
(2)①∵△ABC≌△DEB,∴∠A=∠D=35°,∠EBD=∠C=60°,∴∠ABC=180°-∠A-∠C=85°,∴∠DBC=∠ABC-∠EBD=85°-60°=25°;②∠AFD=∠A+∠AED=∠A+∠EBD+∠D=35°+60°+35°=130°.
26.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
解:(1)∠BAF=∠DCE,∠AFB=∠CED,AB=CD,BF=DE;
(2)∵△ABF≌△CDE,∴∠D=∠B=30°,∴∠EFC=∠D+∠DCF=70°;
(3)BF=6.
27.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
解:∵△ABC≌△DBE,∴∠ABC=∠DBE.
∴∠ABC-∠DBC=∠DBE-∠DBC,
即∠ABD=∠CBE.
∴∠CBE=(∠ABE-∠DBC)=×(160°-30°)=65°.
(2)若AD=DC=3 cm,BC=4.5 cm,求△DCP与△BPE的周长之和.
解:∵△ABC≌△DBE,
∴BE=BC=4.5 cm,DE=AC=AD+DC=6 cm.
∴△DCP与△BPE的周长之和为DC+DP+PC+BP+PE+BE
=(DP+PE)+(BP+PC)+DC+BE=DE+BC+DC+BE
=6+4.5+3+4.5=18(cm).
28.如图,把两个形状、大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;
解:四边形ABCD≌四边形AEFG,
△AFG≌△FAE≌△ACD≌△CAB.
(2)判断△AFC的形状.
解:∵△FAE≌△ACD,
∴AF=AC,∠FAE=∠ACD.
∵四边形ABCD是长方形,
∴∠ADC=90°.∴∠ACD+∠CAD=90°.
∴∠FAE+∠CAD=90°,即∠FAC=90°.
∴△AFC是等腰直角三角形.
29.如图,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)求证:BD=DE+CE.
证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE.
∵AE=AD+DE,∴BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
【解析】要使BD∥CE,则需∠BDE=∠CEA,而由△BAD≌△ACE可知∠ADB=∠CEA,由此可得结果.
解:当△ABD满足∠ADB=90°时,
BD∥CE.理由:∵△BAD≌△ACE,
∴∠ADB=∠CEA=90°.
易知∠BDE=90°,
∴∠CEA=∠BDE=90°.∴BD∥CE.
30.阅读下面的文字,然后回答相关问题:
如图①,若把△ACD沿着直线AC平行移动,它就能和△CBE重合,像这种变换图形位置的方法,叫做平移变换;如图②,若把△ABC沿着直线BC翻折,它就能和△DBC重合,像这种变换图形位置的方法,叫做翻折(或翻转)变换;如图③,若把△AOC绕着点O旋转一定的角度,它将与△EOD重合,像这种变换图形位置的方法,叫做旋转变换.
想一想:(1)如图④,若△ABC≌△DEF,且点B与点E,点C与点F是对应顶点,则进行怎样的图形变换可以使这两个三角形重合
(2)如图⑤,已知△ABF≌△DCE,点E与点F是对应顶点,则△DCE可以看成是由△ABF通过怎样的图形变换得到的
解 (1)先将△ABC沿着直线BF平移,使点B与点E重合,点C与点F重合,再将此三角形沿着EF所在直线翻折便能与△DEF重合.
(2)先将△ABF沿着直线BC平移,使点F与点E重合,再将此三角形绕着点E逆时针旋转180°,便可得到△DCE.(答案均不唯一)
【知识重点】
知识点1 全等形
1. 定义 能够完全重合的两个图形叫做全等形.
全等形的特征 “两相同”与“两无关”.
(1)“两相同”:①形状相同;②大小相同.
(2)“两无关”:①与位置无关;②与方向无关.
2. 全等变换的常见方式 平移、翻折、旋转.
特别解读
●完全重合说明两个图形的周长和面积相等;
●周长或面积相等的两个图形不一定是全等形.
知识点2 全等三角形
1. 全等三角形的相关概念
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形.
(2)全等三角形的对应元素:
①对应顶点:全等三角形中,能够重合的顶点;
②对应边:全等三角形中,能够重合的边;
③对应角:全等三角形中,能够重合的角.
2. 全等三角形的表示方法
全等用符号“≌”表示,读作“全等于”. 记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系,“对边”是指三角形中某个角所对的边,“对角”是指三角形中某条边所对的角.
知识点3 全等三角形的性质
1. 性质 全等三角形的对应边相等,对应角相等.
几何语言:∵△ABC≌△DEF,
∴
2. 拓展 全等三角形的对应元素相等.
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等.
要点提醒
1. 应用全等三角形的性质时,要先确定两个条件:
(1) 两个三角形全等;
(2) 找对应元素.
2. 全等三角形的性质是证明线段、角相等的常用方法.
【经典例题】
【例1】如图是全等形的有________________________________.
解题秘方:根据全等形的定义和特征进行判断.
【例2】如图,已知△ABD≌△CDB,∠ ABD=∠CDB. 写出其对应边和对应角.
解题秘方:根据图形的位置特征确定对应角和对应边.
【例3】如图,将△ABC绕其顶点B顺时针旋转一定角度后得到△DBE,请判断图中△ABC和△DBE是否为全等三角形. 若是,写出其对应边和对应角.
解题秘方:根据图形旋转前后的对应位置找对应关系.
【例4】如图,已知△ABC≌△EDF.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
(1)求证:DC=BF;
(2)求证:AC∥EF.
【例5】如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解题秘方:利用全等三角形的对应角相等,并结合三角形的内角和为180°进行计算.
【同步练习】
一、选择题
1.下列图形中,是全等形的有( )
A.4对 B.3对 C.2对 D.1对
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
第2题图 第3题图 第4题图
3.如图,若△NMQ≌△MNP,且MN=8 cm,NP=6 cm,PM=7 cm,则MQ的长为( )
A.8 cm B.7 cm C.6 cm D.5 cm
4.如图,在△ABC中,D,E分别是AC,BC上的点.若△ADB≌△EDC≌△EDB,则∠C的度数是( )
A.15° B.20° C.25° D.30°
5.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'等于( )
A.20° B.30° C.35° D.40°
第5题图 第6题图 第7题图
6.如图,△AOC≌△BOD,AC=BD,则OA等于( )
A.OC B.OB C.OD D.AC
7.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列表示正确的是( )
A.△ABC≌△AED B.△ABC≌△EAD C.△ABC≌△DEA D.△ABC≌△ADE
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.10cm B.7cm C.5cm D.无法确定
第8题图 第9题图 第10题图
9.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
10.【2021·哈尔滨】如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
二、填空题
11.能够__________的两个图形称为全等形,全等形的______和______都相同.平移、翻折、旋转前后的两个图形________.
12.能够完全_______的两个三角形叫做全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做_________,重合的边叫做________,重合的角叫做__________.
13.全等用符号“______”表示,读作“__________”.记两个三角形全等时,通常把表示对应顶点的字母写在_______的位置上.
14.全等三角形是两个能够完全重合的三角形,因此它们的________边相等,________角相等.
15.已知△ABC与△EDF全等, 其中点A与点E, 点B与点D, 点C与点F是对应顶点, 则对应边为____________________________,对应角为__________________________________,△ABC≌_______.
16.如图,有6个条形方格图,图上由实线围成的图形是全等形的有哪几对?__________________(填序号).
第16题图 第17题图 第18题图
17.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F, 则∠DFB的度数为______.
18.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
19.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
20.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
三、解答题
21.如图,把△ABC绕点A逆时针旋转90 °,得到△ADE, 显然有△ABC≌△ADE,写出所有的对应顶点、对应边和对应角.
22.如图,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
23.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
24.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2 cm,BC=5 cm.
(1)求DE的长.
(2)DB与AC垂直吗?为什么?
25.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°.
①求∠DBC的度数;
②求∠AFD的度数.
26.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
27.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
(2)若AD=DC=3 cm,BC=4.5 cm,求△DCP与△BPE的周长之和.
28.如图,把两个形状、大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;
(2)判断△AFC的形状.
29.如图,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)求证:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
30.阅读下面的文字,然后回答相关问题:
如图①,若把△ACD沿着直线AC平行移动,它就能和△CBE重合,像这种变换图形位置的方法,叫做平移变换;如图②,若把△ABC沿着直线BC翻折,它就能和△DBC重合,像这种变换图形位置的方法,叫做翻折(或翻转)变换;如图③,若把△AOC绕着点O旋转一定的角度,它将与△EOD重合,像这种变换图形位置的方法,叫做旋转变换.
想一想:(1)如图④,若△ABC≌△DEF,且点B与点E,点C与点F是对应顶点,则进行怎样的图形变换可以使这两个三角形重合
(2)如图⑤,已知△ABF≌△DCE,点E与点F是对应顶点,则△DCE可以看成是由△ABF通过怎样的图形变换得到的
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图是全等形的有________________________________.
【答案】①和⑨、②和③、④和⑧、 和
解题秘方:根据全等形的定义和特征进行判断.
解:上述图形中,⑤和⑦形状相同,但大小不同;⑥和⑩大小、形状都不同. ①和⑨、②和③、 和 尽管方向不同,但大小、形状完全相同,所以它们是全等形;④和⑧都是五角星,大小、形状都相同,是全等形.
确定两个图形全等的方法.
1. 条件判断法:(1) 形状相同;(2) 大小相等,是不是全等形与位置无关.
2. 重合判断法:通过平移、翻折、旋转等方法把两个图形叠合在一起,看它们能否完全重合.
【例2】如图,已知△ABD≌△CDB,∠ ABD=∠CDB. 写出其对应边和对应角.
解题秘方:根据图形的位置特征确定对应角和对应边.
解:BD和DB,AD和CB,AB和CD是对应边;∠A 和∠C,∠ABD和∠CDB,∠ADB和∠CBD是对应角.
方法点拨:利用图形位置关系找对应边和对应角:
①公共角(对顶角)为对应角,公共边为对应边;
②对应角的对边为对应边,两个对应角所夹的边是对应边;
③对应边的对角为对应角,两条对应边所夹的角是对应角.
【例3】如图,将△ABC绕其顶点B顺时针旋转一定角度后得到△DBE,请判断图中△ABC和△DBE是否为全等三角形. 若是,写出其对应边和对应角.
解题秘方:根据图形旋转前后的对应位置找对应关系.
解:△ABC≌△DBE.
AB和DB,AC和DE,BC和BE是对应边;
∠A和∠BDE,∠ABC和∠DBE,∠C和∠E是对应角.
【例4】如图,已知△ABC≌△EDF.
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题.
(1)求证:DC=BF;
证明:∵△ABC≌△EDF,∴ DF=BC.
∴ DF-CF=BC-CF,即DC=BF.
(2)求证:AC∥EF.
∵△ABC≌△EDF,∴∠ACB=∠EFD.
∴ AC∥EF.
【例5】如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解题秘方:利用全等三角形的对应角相等,并结合三角形的内角和为180°进行计算.
解:∵△ADB≌△EDB≌△EDC,
∴∠ABD=∠EBD=∠C,∠A=∠BED=∠CED.
又∵∠BED+∠CED=180°,∴∠BED=∠CED=90°.
∴∠A=90°.
∴∠ABD+∠EBD+∠C=180°-∠A=90°.
∴ 3∠C=90°.∴∠C=30°.
【同步练习】
一、选择题
1.下列图形中,是全等形的有( B )
A.4对 B.3对 C.2对 D.1对
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( B )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
【答案】∵△ABC≌△ADE,∴AB=AD,AC=AE,∠ABC=∠ADE,∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故选B.
第2题图 第3题图 第4题图
3.如图,若△NMQ≌△MNP,且MN=8 cm,NP=6 cm,PM=7 cm,则MQ的长为( C )
A.8 cm B.7 cm C.6 cm D.5 cm
【答案】因为△NMQ≌△MNP,所以MQ与NP是对应边,即MQ=NP=6 cm.
4.如图,在△ABC中,D,E分别是AC,BC上的点.若△ADB≌△EDC≌△EDB,则∠C的度数是( D )
A.15° B.20° C.25° D.30°
【答案】 ∵△EDB≌△EDC,
∴∠DEB=∠DEC=90°.
∵△ADB≌△EDB,
∴∠DAB=∠DEB=90°.
∵△ADB≌△EDB≌△EDC,
∴∠C=∠ABD=∠CBD=30°.
5.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'等于( B )
A.20° B.30° C.35° D.40°
【答案】因为△ACB≌△A'CB',所以∠ACB=∠A'CB',所以∠ACB-∠A'CB=∠A'CB'-∠A'CB,即∠ACA'=∠BCB'=30°.
第5题图 第6题图 第7题图
6.如图,△AOC≌△BOD,AC=BD,则OA等于( B )
A.OC B.OB C.OD D.AC
7.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列表示正确的是( D )
A.△ABC≌△AED B.△ABC≌△EAD C.△ABC≌△DEA D.△ABC≌△ADE
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( A )
A.10cm B.7cm C.5cm D.无法确定
第8题图 第9题图 第10题图
9.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( D )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
10.【2021·哈尔滨】如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( B )
A.30° B.25° C.35° D.65°
二、填空题
11.能够__________的两个图形称为全等形,全等形的______和______都相同.平移、翻折、旋转前后的两个图形________.
【答案】完全重合 形状 大小 全等
12.能够完全_______的两个三角形叫做全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做_________,重合的边叫做________,重合的角叫做__________.
【答案】重合 对应顶点 对应边 对应角
13.全等用符号“______”表示,读作“__________”.记两个三角形全等时,通常把表示对应顶点的字母写在_______的位置上.
【答案】≌ 全等于 对应
14.全等三角形是两个能够完全重合的三角形,因此它们的________边相等,________角相等.
【答案】对应 对应
15.已知△ABC与△EDF全等, 其中点A与点E, 点B与点D, 点C与点F是对应顶点, 则对应边为____________________________,对应角为__________________________________,△ABC≌_______.
【答案】AB与ED,AC与EF,BC与DF
∠A与∠E,∠B与∠D,∠C与∠F
△EDF
16.如图,有6个条形方格图,图上由实线围成的图形是全等形的有哪几对?__________________(填序号).
【答案】①和⑥,②③和⑤
第16题图 第17题图 第18题图
17.如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F, 则∠DFB的度数为______.
【答案】20°
18.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
【答案】∠DAE DE
19.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
【答案】11cm
20.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
【答案】②④
三、解答题
21.如图,把△ABC绕点A逆时针旋转90 °,得到△ADE, 显然有△ABC≌△ADE,写出所有的对应顶点、对应边和对应角.
解:对应顶点:A对应A,B对应D,C对应E;
对应边:AB对应AD,AC对应AE,BC对应DE;对应角:∠BAC对应∠DAE,∠B对应∠D,∠C对应∠E.
22.如图,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
解:AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.∴AD⊥BC.
23.如图,D,E分别是△ABC的边AC,BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数.
解:∵△EDB≌△EDC,∴∠DEB=∠DEC.
∵∠DEB+∠DEC=180°,∴∠DEB=∠DEC=90°.
∵△ADB≌△EDB≌△EDC,∴∠ADB=∠EDB=∠EDC.
∵∠ADB+∠EDB+∠EDC=180°,
∴∠ADB=∠EDB=∠EDC=60°.
∴∠C=30°.
24.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2 cm,BC=5 cm.
(1)求DE的长.
解:∵△ABD≌△EBC,
∴BD=BC=5 cm,BE=AB=2 cm.
∴DE=BD-BE=3 cm.
(2)DB与AC垂直吗?为什么?
解:DB与AC垂直.理由如下:
∵△ABD≌△EBC,∴∠ABD=∠EBC.
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°.
∴∠EBC=90°,即DB与AC垂直.
25.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°.
①求∠DBC的度数;
②求∠AFD的度数.
解:(1)3;
(2)①∵△ABC≌△DEB,∴∠A=∠D=35°,∠EBD=∠C=60°,∴∠ABC=180°-∠A-∠C=85°,∴∠DBC=∠ABC-∠EBD=85°-60°=25°;②∠AFD=∠A+∠AED=∠A+∠EBD+∠D=35°+60°+35°=130°.
26.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
解:(1)∠BAF=∠DCE,∠AFB=∠CED,AB=CD,BF=DE;
(2)∵△ABF≌△CDE,∴∠D=∠B=30°,∴∠EFC=∠D+∠DCF=70°;
(3)BF=6.
27.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
解:∵△ABC≌△DBE,∴∠ABC=∠DBE.
∴∠ABC-∠DBC=∠DBE-∠DBC,
即∠ABD=∠CBE.
∴∠CBE=(∠ABE-∠DBC)=×(160°-30°)=65°.
(2)若AD=DC=3 cm,BC=4.5 cm,求△DCP与△BPE的周长之和.
解:∵△ABC≌△DBE,
∴BE=BC=4.5 cm,DE=AC=AD+DC=6 cm.
∴△DCP与△BPE的周长之和为DC+DP+PC+BP+PE+BE
=(DP+PE)+(BP+PC)+DC+BE=DE+BC+DC+BE
=6+4.5+3+4.5=18(cm).
28.如图,把两个形状、大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;
解:四边形ABCD≌四边形AEFG,
△AFG≌△FAE≌△ACD≌△CAB.
(2)判断△AFC的形状.
解:∵△FAE≌△ACD,
∴AF=AC,∠FAE=∠ACD.
∵四边形ABCD是长方形,
∴∠ADC=90°.∴∠ACD+∠CAD=90°.
∴∠FAE+∠CAD=90°,即∠FAC=90°.
∴△AFC是等腰直角三角形.
29.如图,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)求证:BD=DE+CE.
证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE.
∵AE=AD+DE,∴BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
【解析】要使BD∥CE,则需∠BDE=∠CEA,而由△BAD≌△ACE可知∠ADB=∠CEA,由此可得结果.
解:当△ABD满足∠ADB=90°时,
BD∥CE.理由:∵△BAD≌△ACE,
∴∠ADB=∠CEA=90°.
易知∠BDE=90°,
∴∠CEA=∠BDE=90°.∴BD∥CE.
30.阅读下面的文字,然后回答相关问题:
如图①,若把△ACD沿着直线AC平行移动,它就能和△CBE重合,像这种变换图形位置的方法,叫做平移变换;如图②,若把△ABC沿着直线BC翻折,它就能和△DBC重合,像这种变换图形位置的方法,叫做翻折(或翻转)变换;如图③,若把△AOC绕着点O旋转一定的角度,它将与△EOD重合,像这种变换图形位置的方法,叫做旋转变换.
想一想:(1)如图④,若△ABC≌△DEF,且点B与点E,点C与点F是对应顶点,则进行怎样的图形变换可以使这两个三角形重合
(2)如图⑤,已知△ABF≌△DCE,点E与点F是对应顶点,则△DCE可以看成是由△ABF通过怎样的图形变换得到的
解 (1)先将△ABC沿着直线BF平移,使点B与点E重合,点C与点F重合,再将此三角形沿着EF所在直线翻折便能与△DEF重合.
(2)先将△ABF沿着直线BC平移,使点F与点E重合,再将此三角形绕着点E逆时针旋转180°,便可得到△DCE.(答案均不唯一)
