12.2.1 运用“边边边”证三角形全等 同步练习(含答案)
文档属性
| 名称 | 12.2.1 运用“边边边”证三角形全等 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 22:15:45 | ||
图片预览



文档简介
12.2 三角形全等的判定
第1课时 运用“边边边”证三角形全等
【知识重点】
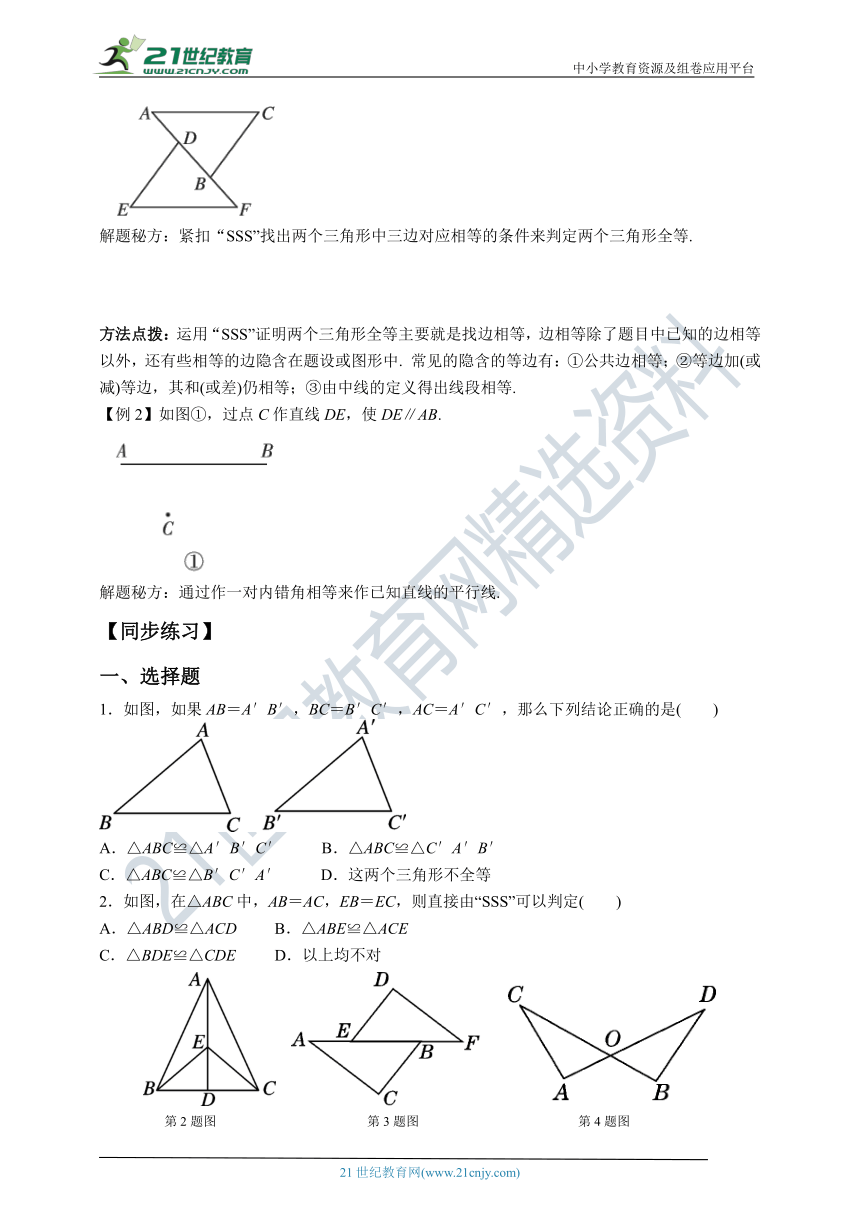
知识点1 利用“SSS”判定三角形全等
1.基本事实 三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2.书写格式 如图,
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SSS).
特别提醒
在列举两个三角形全等的条件时,应把三个条件按顺序排列(一般是把同一个三角形的三个条件放在等号的同一侧),并用大括号将其括起来.
知识点2 用尺规作一个角等于已知角
作一个角等于已知角 已知∠AOB(如图①),求作∠A′O′B′,使∠A′O′B′=∠AOB.
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与(2)中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′即为所求作的角(如图②).
特别解读
作一个角等于已知角,是利用尺规作一个三角形与已知三角形全等,利用的判定方法是“SSS”,然后利用全等三角形的性质——对应角相等,说明作出的角等于已知角.
【经典例题】
【例1】如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB. 求证:△ABC≌△FDE.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
方法点拨:运用“SSS”证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的隐含的等边有:①公共边相等;②等边加(或减)等边,其和(或差)仍相等;③由中线的定义得出线段相等.
【例2】如图①,过点C作直线DE,使DE∥AB.
解题秘方:通过作一对内错角相等来作已知直线的平行线.
【同步练习】
一、选择题
1.如图,如果AB=A′B′,BC=B′C′,AC=A′C′,那么下列结论正确的是( )
A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′ D.这两个三角形不全等
2.如图,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上均不对
第2题图 第3题图 第4题图
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC≌△FED时,下面的4个条件:
①AE=FB;②AB=FE;③AE=BE;④BF=BE.
其中可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )
A.120° B.125° C.130° D.135°
5.如图,已知AB=CD,BC=DA,下列结论:
①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD,BC∥DA.
其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图 第7题图
6.如图,已知AB=6,AC=9,DC=6,要使△ABD≌△DCA,还需添加的条件是( )
A.DA=5 B.DA=6 C.DB=9 D.DB=6
7.如图,AB=AD,AC=AE,BC=DE,∠A=60°,∠E=30°,则∠EBC的度数为( )
A.30° B.45° C.60° D.90°
8.如图,已知AB=AC,D为BC的中点,下列结论:
①∠B=∠C;②AD平分∠BAC;③AD⊥BC;④△ABD≌△ACD.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
第8题图 第9题图 第10题图
9.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠ACE=30° D.∠1=70°
10.如图,在△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
二、填空题
11.如图,下列三角形中,与△ABC全等的是___.
12.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB的依据是_________.
13.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= .
第13题图 第14题图 第15题图
14.如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为 ,∠APB的度数为 .
15.如图,已知AB=AD,AC=AE,BC=DE,直线BC与AD,DE分别交于点F,G,且∠DGB=65°,∠EAB=120°,则∠CAD的度数为_________.
三、解答题
16.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC. 求证:△ABC≌△CDA.
17.如图,AC=BD,BC=AD.求证:△ABC≌△BAD.
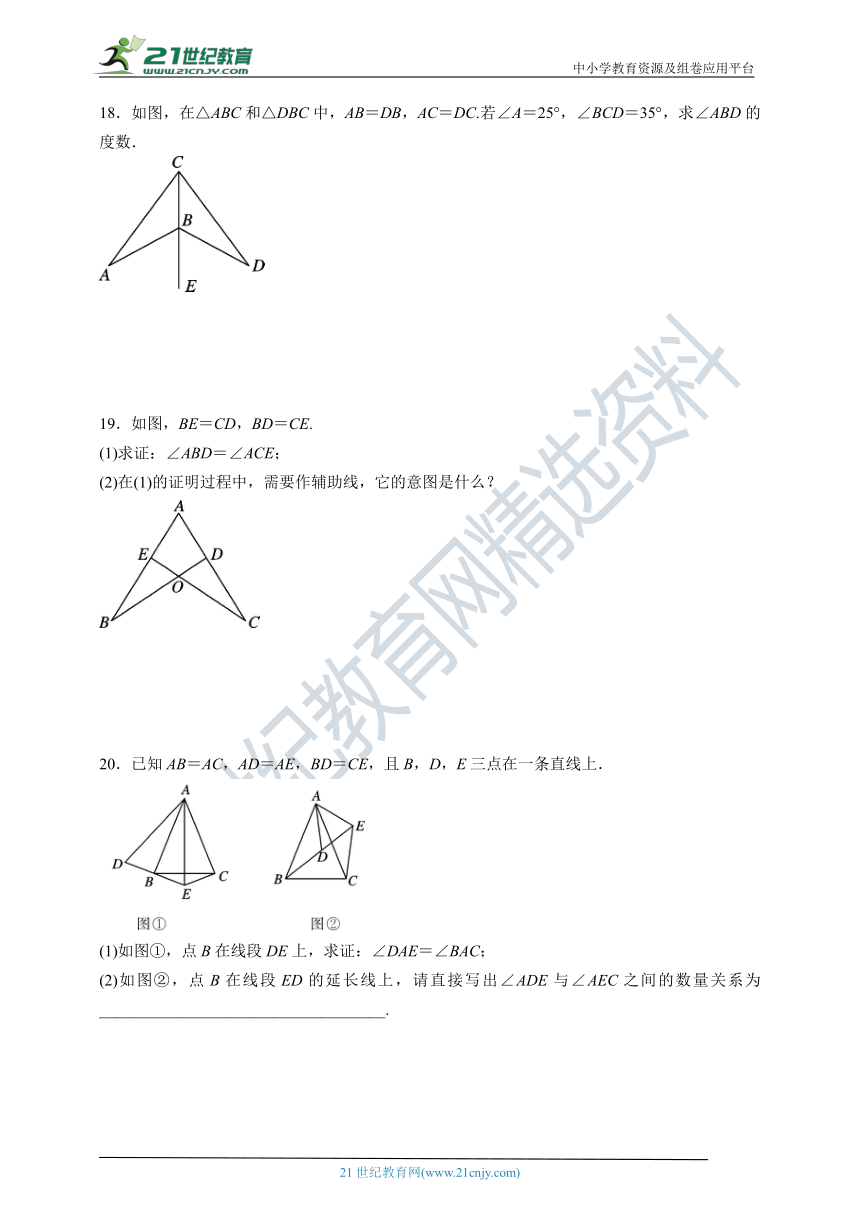
18.如图,在△ABC和△DBC中,AB=DB,AC=DC.若∠A=25°,∠BCD=35°,求∠ABD的度数.
19.如图,BE=CD,BD=CE.
(1)求证:∠ABD=∠ACE;
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
20.已知AB=AC,AD=AE,BD=CE,且B,D,E三点在一条直线上.
(1)如图①,点B在线段DE上,求证:∠DAE=∠BAC;
(2)如图②,点B在线段ED的延长线上,请直接写出∠ADE与∠AEC之间的数量关系为____________________________________.
21.如图,在△ABC中,AC=BC,D是边AB上一点,AE⊥CD于点E,BF⊥CD交CD的延长线于点F,若CE=BF,AE=EF+BF.
(1)求证:∠ACE=∠CBF.
(2)判断直线AC与BC的位置关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB. 求证:△ABC≌△FDE.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
证明:∵ AD=FB,∴ AD+DB=FB+DB,即AB=FD.
在△ABC和△FDE中,
∴△ABC≌△FDE(SSS).
方法点拨:运用“SSS”证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的隐含的等边有:①公共边相等;②等边加(或减)等边,其和(或差)仍相等;③由中线的定义得出线段相等.
【例2】如图①,过点C作直线DE,使DE∥AB.
解题秘方:通过作一对内错角相等来作已知直线的平行线.
解:作法如下:
(1)过点C作直线MN与AB相交,交点为F;
(2)在直线MN的右侧作∠FCE,使∠FCE=∠AFC;
(3)反向延长CE,则直线DE即为所求(如图②).
【同步练习】
一、选择题
1.如图,如果AB=A′B′,BC=B′C′,AC=A′C′,那么下列结论正确的是( A )
A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′ D.这两个三角形不全等
2.如图,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( B )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上均不对
第2题图 第3题图 第4题图
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC≌△FED时,下面的4个条件:
①AE=FB;②AB=FE;③AE=BE;④BF=BE.
其中可利用的是( A )
A.①或② B.②或③ C.①或③ D.①或④
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( B )
A.120° B.125° C.130° D.135°
5.如图,已知AB=CD,BC=DA,下列结论:
①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD,BC∥DA.
其中正确的结论有( D )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图 第7题图
6.如图,已知AB=6,AC=9,DC=6,要使△ABD≌△DCA,还需添加的条件是( C )
A.DA=5 B.DA=6 C.DB=9 D.DB=6
7.如图,AB=AD,AC=AE,BC=DE,∠A=60°,∠E=30°,则∠EBC的度数为( D )
A.30° B.45° C.60° D.90°
8.如图,已知AB=AC,D为BC的中点,下列结论:
①∠B=∠C;②AD平分∠BAC;③AD⊥BC;④△ABD≌△ACD.
其中正确的个数为( D )
A.1个 B.2个 C.3个 D.4个
第8题图 第9题图 第10题图
9.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( C )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠ACE=30° D.∠1=70°
10.如图,在△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有( C )
A.2对 B.3对 C.4对 D.5对
二、填空题
11.如图,下列三角形中,与△ABC全等的是___.
【答案】③
12.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB的依据是_________.
【答案】SSS
13.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= .
【答案】40°
第13题图 第14题图 第15题图
14.如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为 ,∠APB的度数为 .
【答案】40° 40°
15.如图,已知AB=AD,AC=AE,BC=DE,直线BC与AD,DE分别交于点F,G,且∠DGB=65°,∠EAB=120°,则∠CAD的度数为_________.
【答案】10°
三、解答题
16.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC. 求证:△ABC≌△CDA.
证明:在△ABC和△CDA中,
∴△ABC≌△CDA(SSS).
17.如图,AC=BD,BC=AD.
求证:△ABC≌△BAD.
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SSS).
18.如图,在△ABC和△DBC中,AB=DB,AC=DC.若∠A=25°,∠BCD=35°,求∠ABD的度数.
解:在△ABC和△DBC中,
∴△ABC≌△DBC(SSS).
∴∠A=∠D,∠ACB=∠DCB,∠ABC=∠DBC.
∴∠ABE=∠DBE.
∵∠A=25°,∠BCD=∠ACB=35°,
∴∠ABE=∠A+∠ACB=25°+35°=60°.
∴∠ABD=2∠ABE=120°.
19.如图,BE=CD,BD=CE.
(1)求证:∠ABD=∠ACE;
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
解:(1)证明:连接BC,可用SSS证明△BEC≌△CDB,
可得∠EBC=∠DCB,
∠1=∠2,
∴∠EBC-∠2=∠DCB-∠1,
∴∠ABD=∠ACE.
(2)构造全等三角形.
20.已知AB=AC,AD=AE,BD=CE,且B,D,E三点在一条直线上.
(1)如图①,点B在线段DE上,求证:∠DAE=∠BAC;
(2)如图②,点B在线段ED的延长线上,请直接写出∠ADE与∠AEC之间的数量关系为____________________________________.
解:(1)证明:在△ADB和△AEC中,
∴△ADB≌△AEC.∴∠DAB=∠EAC,
∴∠DAB+∠BAE=∠BAE+∠EAC,
∴∠DAE=∠BAC.
(2)【答案】∠ADE+∠AEC=180°
21.如图,在△ABC中,AC=BC,D是边AB上一点,AE⊥CD于点E,BF⊥CD交CD的延长线于点F,若CE=BF,AE=EF+BF.
(1)求证:∠ACE=∠CBF.
证明:∵AE=EF+BF,CE=BF,
∴AE=EF+CE=CF.
在△ACE和△CBF中,
∴△ACE≌△CBF(SSS),∴∠ACE=∠CBF.
(2)判断直线AC与BC的位置关系,并说明理由.
解:AC⊥BC.理由如下:
由(1)知△ACE≌△CBF,∴∠CAE=∠BCF.
∵AE⊥CF,∴∠AEC=90°,
∴∠CAE+∠ACE=90°,
∴∠BCF+∠ACE=90°,
∴∠ACB=90°,即AC⊥BC.
第1课时 运用“边边边”证三角形全等
【知识重点】
知识点1 利用“SSS”判定三角形全等
1.基本事实 三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2.书写格式 如图,
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SSS).
特别提醒
在列举两个三角形全等的条件时,应把三个条件按顺序排列(一般是把同一个三角形的三个条件放在等号的同一侧),并用大括号将其括起来.
知识点2 用尺规作一个角等于已知角
作一个角等于已知角 已知∠AOB(如图①),求作∠A′O′B′,使∠A′O′B′=∠AOB.
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与(2)中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′即为所求作的角(如图②).
特别解读
作一个角等于已知角,是利用尺规作一个三角形与已知三角形全等,利用的判定方法是“SSS”,然后利用全等三角形的性质——对应角相等,说明作出的角等于已知角.
【经典例题】
【例1】如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB. 求证:△ABC≌△FDE.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
方法点拨:运用“SSS”证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的隐含的等边有:①公共边相等;②等边加(或减)等边,其和(或差)仍相等;③由中线的定义得出线段相等.
【例2】如图①,过点C作直线DE,使DE∥AB.
解题秘方:通过作一对内错角相等来作已知直线的平行线.
【同步练习】
一、选择题
1.如图,如果AB=A′B′,BC=B′C′,AC=A′C′,那么下列结论正确的是( )
A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′ D.这两个三角形不全等
2.如图,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上均不对
第2题图 第3题图 第4题图
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC≌△FED时,下面的4个条件:
①AE=FB;②AB=FE;③AE=BE;④BF=BE.
其中可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )
A.120° B.125° C.130° D.135°
5.如图,已知AB=CD,BC=DA,下列结论:
①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD,BC∥DA.
其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图 第7题图
6.如图,已知AB=6,AC=9,DC=6,要使△ABD≌△DCA,还需添加的条件是( )
A.DA=5 B.DA=6 C.DB=9 D.DB=6
7.如图,AB=AD,AC=AE,BC=DE,∠A=60°,∠E=30°,则∠EBC的度数为( )
A.30° B.45° C.60° D.90°
8.如图,已知AB=AC,D为BC的中点,下列结论:
①∠B=∠C;②AD平分∠BAC;③AD⊥BC;④△ABD≌△ACD.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
第8题图 第9题图 第10题图
9.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠ACE=30° D.∠1=70°
10.如图,在△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
二、填空题
11.如图,下列三角形中,与△ABC全等的是___.
12.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB的依据是_________.
13.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= .
第13题图 第14题图 第15题图
14.如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为 ,∠APB的度数为 .
15.如图,已知AB=AD,AC=AE,BC=DE,直线BC与AD,DE分别交于点F,G,且∠DGB=65°,∠EAB=120°,则∠CAD的度数为_________.
三、解答题
16.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC. 求证:△ABC≌△CDA.
17.如图,AC=BD,BC=AD.求证:△ABC≌△BAD.
18.如图,在△ABC和△DBC中,AB=DB,AC=DC.若∠A=25°,∠BCD=35°,求∠ABD的度数.
19.如图,BE=CD,BD=CE.
(1)求证:∠ABD=∠ACE;
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
20.已知AB=AC,AD=AE,BD=CE,且B,D,E三点在一条直线上.
(1)如图①,点B在线段DE上,求证:∠DAE=∠BAC;
(2)如图②,点B在线段ED的延长线上,请直接写出∠ADE与∠AEC之间的数量关系为____________________________________.
21.如图,在△ABC中,AC=BC,D是边AB上一点,AE⊥CD于点E,BF⊥CD交CD的延长线于点F,若CE=BF,AE=EF+BF.
(1)求证:∠ACE=∠CBF.
(2)判断直线AC与BC的位置关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB. 求证:△ABC≌△FDE.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
证明:∵ AD=FB,∴ AD+DB=FB+DB,即AB=FD.
在△ABC和△FDE中,
∴△ABC≌△FDE(SSS).
方法点拨:运用“SSS”证明两个三角形全等主要就是找边相等,边相等除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的隐含的等边有:①公共边相等;②等边加(或减)等边,其和(或差)仍相等;③由中线的定义得出线段相等.
【例2】如图①,过点C作直线DE,使DE∥AB.
解题秘方:通过作一对内错角相等来作已知直线的平行线.
解:作法如下:
(1)过点C作直线MN与AB相交,交点为F;
(2)在直线MN的右侧作∠FCE,使∠FCE=∠AFC;
(3)反向延长CE,则直线DE即为所求(如图②).
【同步练习】
一、选择题
1.如图,如果AB=A′B′,BC=B′C′,AC=A′C′,那么下列结论正确的是( A )
A.△ABC≌△A′B′C′ B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′ D.这两个三角形不全等
2.如图,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( B )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上均不对
第2题图 第3题图 第4题图
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC≌△FED时,下面的4个条件:
①AE=FB;②AB=FE;③AE=BE;④BF=BE.
其中可利用的是( A )
A.①或② B.②或③ C.①或③ D.①或④
4.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( B )
A.120° B.125° C.130° D.135°
5.如图,已知AB=CD,BC=DA,下列结论:
①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD,BC∥DA.
其中正确的结论有( D )
A.0个 B.1个 C.2个 D.3个
第5题图 第6题图 第7题图
6.如图,已知AB=6,AC=9,DC=6,要使△ABD≌△DCA,还需添加的条件是( C )
A.DA=5 B.DA=6 C.DB=9 D.DB=6
7.如图,AB=AD,AC=AE,BC=DE,∠A=60°,∠E=30°,则∠EBC的度数为( D )
A.30° B.45° C.60° D.90°
8.如图,已知AB=AC,D为BC的中点,下列结论:
①∠B=∠C;②AD平分∠BAC;③AD⊥BC;④△ABD≌△ACD.
其中正确的个数为( D )
A.1个 B.2个 C.3个 D.4个
第8题图 第9题图 第10题图
9.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( C )
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠ACE=30° D.∠1=70°
10.如图,在△ABC中,AB=AC,E,D,F是BC边的四等分点,AE=AF,则图中全等三角形共有( C )
A.2对 B.3对 C.4对 D.5对
二、填空题
11.如图,下列三角形中,与△ABC全等的是___.
【答案】③
12.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.请你根据所学的三角形全等的有关知识,说明画出∠A′O′B′=∠AOB的依据是_________.
【答案】SSS
13.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= .
【答案】40°
第13题图 第14题图 第15题图
14.如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为 ,∠APB的度数为 .
【答案】40° 40°
15.如图,已知AB=AD,AC=AE,BC=DE,直线BC与AD,DE分别交于点F,G,且∠DGB=65°,∠EAB=120°,则∠CAD的度数为_________.
【答案】10°
三、解答题
16.如图,在四边形ABCD中,AB=CD,AD=CB,连接AC. 求证:△ABC≌△CDA.
证明:在△ABC和△CDA中,
∴△ABC≌△CDA(SSS).
17.如图,AC=BD,BC=AD.
求证:△ABC≌△BAD.
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SSS).
18.如图,在△ABC和△DBC中,AB=DB,AC=DC.若∠A=25°,∠BCD=35°,求∠ABD的度数.
解:在△ABC和△DBC中,
∴△ABC≌△DBC(SSS).
∴∠A=∠D,∠ACB=∠DCB,∠ABC=∠DBC.
∴∠ABE=∠DBE.
∵∠A=25°,∠BCD=∠ACB=35°,
∴∠ABE=∠A+∠ACB=25°+35°=60°.
∴∠ABD=2∠ABE=120°.
19.如图,BE=CD,BD=CE.
(1)求证:∠ABD=∠ACE;
(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?
解:(1)证明:连接BC,可用SSS证明△BEC≌△CDB,
可得∠EBC=∠DCB,
∠1=∠2,
∴∠EBC-∠2=∠DCB-∠1,
∴∠ABD=∠ACE.
(2)构造全等三角形.
20.已知AB=AC,AD=AE,BD=CE,且B,D,E三点在一条直线上.
(1)如图①,点B在线段DE上,求证:∠DAE=∠BAC;
(2)如图②,点B在线段ED的延长线上,请直接写出∠ADE与∠AEC之间的数量关系为____________________________________.
解:(1)证明:在△ADB和△AEC中,
∴△ADB≌△AEC.∴∠DAB=∠EAC,
∴∠DAB+∠BAE=∠BAE+∠EAC,
∴∠DAE=∠BAC.
(2)【答案】∠ADE+∠AEC=180°
21.如图,在△ABC中,AC=BC,D是边AB上一点,AE⊥CD于点E,BF⊥CD交CD的延长线于点F,若CE=BF,AE=EF+BF.
(1)求证:∠ACE=∠CBF.
证明:∵AE=EF+BF,CE=BF,
∴AE=EF+CE=CF.
在△ACE和△CBF中,
∴△ACE≌△CBF(SSS),∴∠ACE=∠CBF.
(2)判断直线AC与BC的位置关系,并说明理由.
解:AC⊥BC.理由如下:
由(1)知△ACE≌△CBF,∴∠CAE=∠BCF.
∵AE⊥CF,∴∠AEC=90°,
∴∠CAE+∠ACE=90°,
∴∠BCF+∠ACE=90°,
∴∠ACB=90°,即AC⊥BC.
