12.2.2运用“边角边”证三角形全等 同步练习(含答案)
文档属性
| 名称 | 12.2.2运用“边角边”证三角形全等 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 11:36:19 | ||
图片预览


文档简介
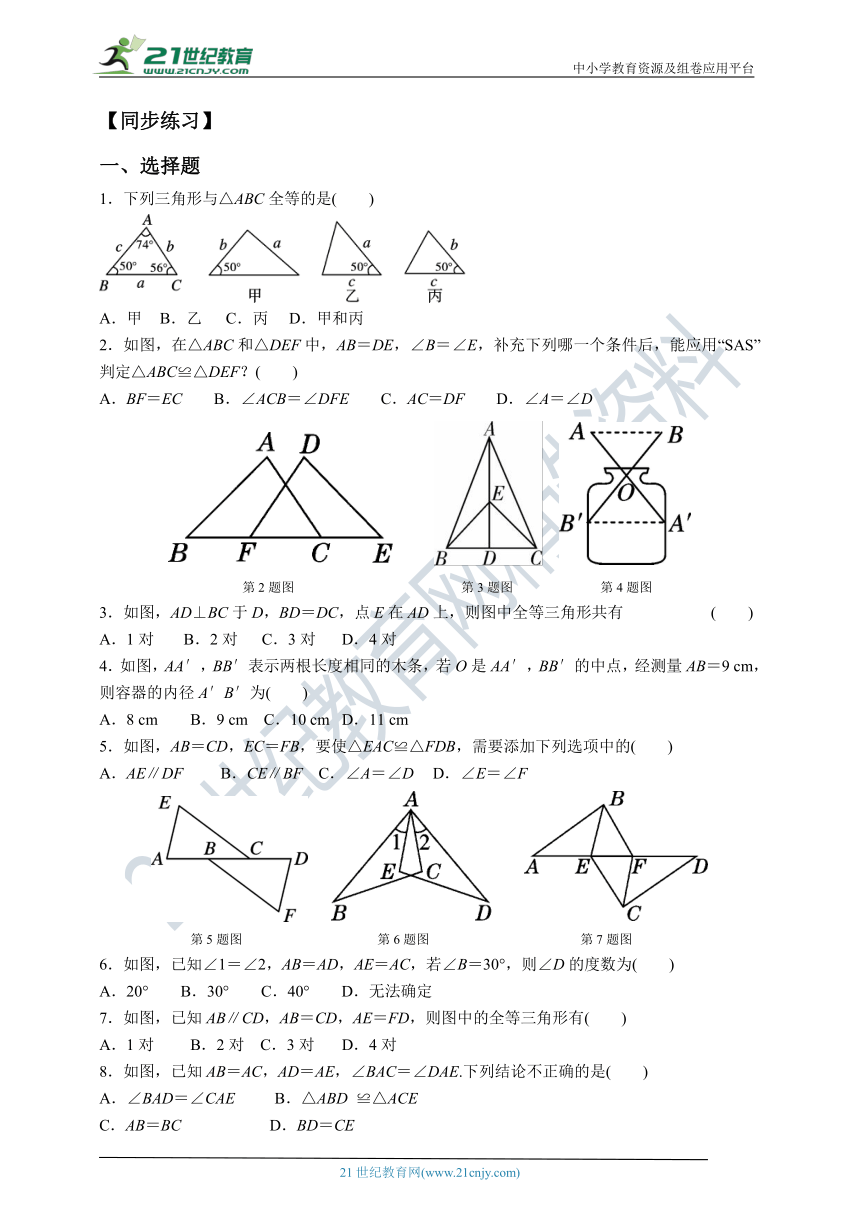
12.2 三角形全等的判定
第2课时 运用“边角边”证三角形全等
【知识重点】
知识点 利用“SAS”判定三角形全等
1. 基本事实 两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2. 书写格式 如图,
在△ABC和△A′B′C′中 ,
∴△ABC≌△A′B′C′(SAS).
要点提醒
1. 相等的元素:两边及这两边的夹角.
2. 书写顺序:边→角→边.
特别解读
两边和其中一边的对角分别相等的两个三角形不一定全等.
【经典例题】
【例】如图,点C是AB的中点,AD=CE, 且AD∥ CE. 求证:△ACD≌△CBE.
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“SAS”判定两个三角形全等.
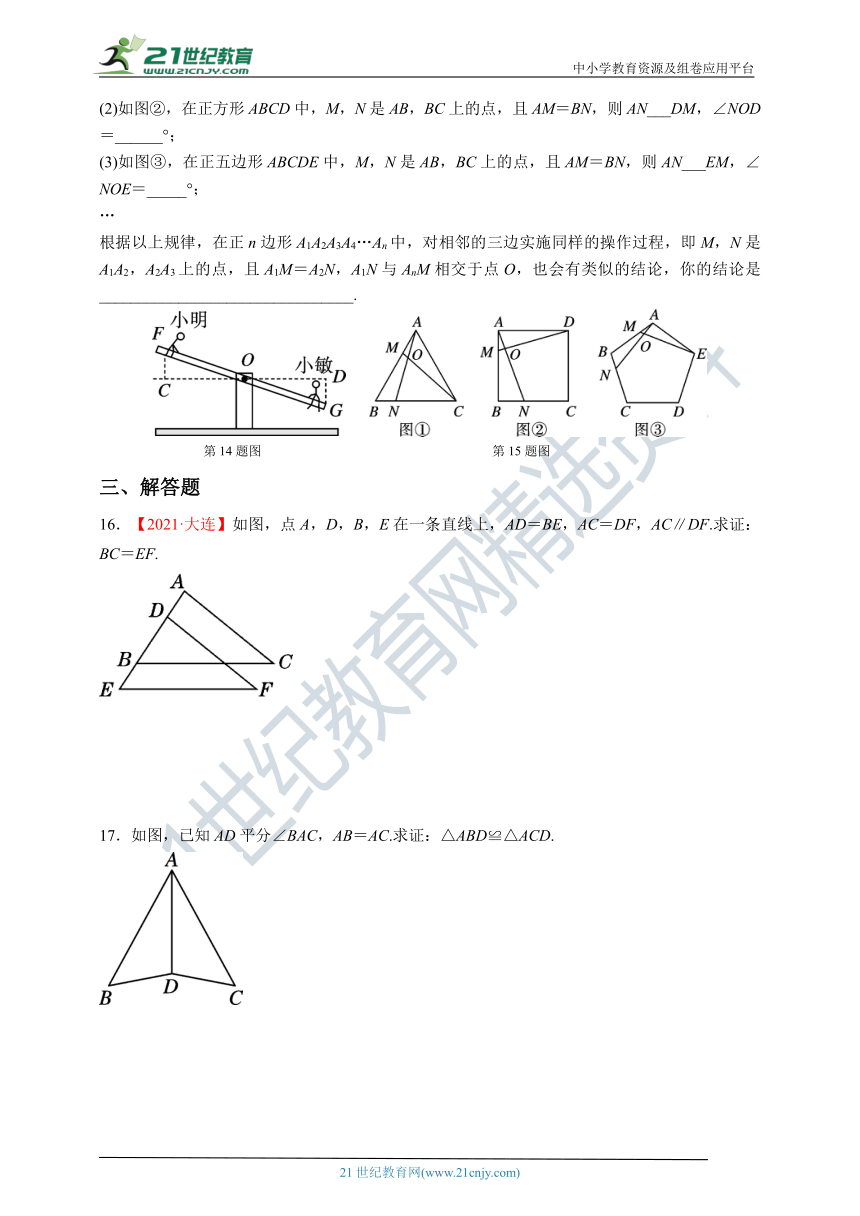
【同步练习】
一、选择题
1.下列三角形与△ABC全等的是( )
A.甲 B.乙 C.丙 D.甲和丙
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( )
A.BF=EC B.∠ACB=∠DFE C.AC=DF D.∠A=∠D
第2题图 第3题图 第4题图
3.如图,AD⊥BC于D,BD=DC,点E在AD上,则图中全等三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
4.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm B.9 cm C.10 cm D.11 cm
5.如图,AB=CD,EC=FB,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AE∥DF B.CE∥BF C.∠A=∠D D.∠E=∠F
第5题图 第6题图 第7题图
6.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( )
A.20° B.30° C.40° D.无法确定
7.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
A.∠BAD=∠CAE B.△ABD ≌△ACE
C.AB=BC D.BD=CE
第8题图 第9题图 第10题图
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.225°
10.在△ABC中,AB=AC,求证:∠B=∠C.
证明:如图,作______.
在△ABD和△ACD中,
∴△ABD≌△ACD,
∴∠B=∠C.
其中,横线上应补充的条件是( )
A.BC边上的高AD B.BC边上的中线AD
C.∠A的平分线AD D.以上都不对
二、填空题
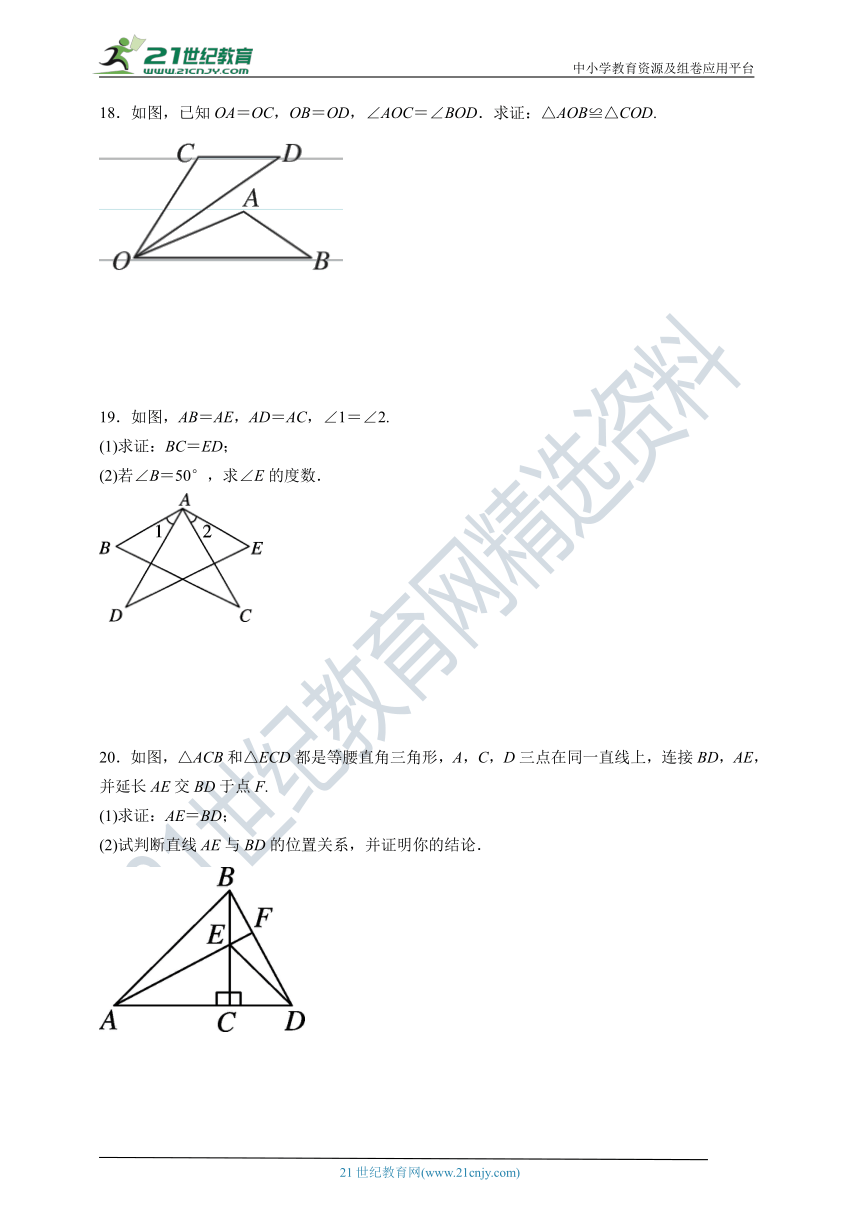
11.【2021·济宁】如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件______________________,使△ABC≌△ADC.
第11题图 第12题图 第13题图
12.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE= .
13.如图,有一块三角形的镜子,马虎不小心将其打破成了1,2两块,现在需要配成同样大小的一块,为了方便起见,只要带上第___块,其理由是_______________ _____________________的两个三角形全等.
14.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)离地面的距离是50 cm,当小敏从水平位置CD下降30 cm时,这时小明离地面的高度是_____________.
15.观察下列结论:
(1)如图①,在正三角形ABC中,M,N是AB,BC上的点,且AM=BN,则AN___CM,∠NOC=______°;
(2)如图②,在正方形ABCD中,M,N是AB,BC上的点,且AM=BN,则AN___DM,∠NOD=______°;
(3)如图③,在正五边形ABCDE中,M,N是AB,BC上的点,且AM=BN,则AN___EM,∠NOE=_____°;
…
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于点O,也会有类似的结论,你的结论是________________________________.
第14题图 第15题图
三、解答题
16.【2021·大连】如图,点A,D,B,E在一条直线上,AD=BE,AC=DF,AC∥DF.求证:BC=EF.
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
18.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
19.如图,AB=AE,AD=AC,∠1=∠2.
(1)求证:BC=ED;
(2)若∠B=50°,求∠E的度数.
20.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于点F.
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
21.如图,在△ABC中,AB>AC,AD是BC边上的中线.
求证:(AB-AC)<AD<(AB+AC).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例】如图,点C是AB的中点,AD=CE, 且AD∥ CE. 求证:△ACD≌△CBE.
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“SAS”判定两个三角形全等.
证明:∵点C是AB的中点,∴ AC=CB.
∵ AD∥CE,∴∠CAD=∠BCE.
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
【同步练习】
一、选择题
1.下列三角形与△ABC全等的是( B )
A.甲 B.乙 C.丙 D.甲和丙
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( A )
A.BF=EC B.∠ACB=∠DFE C.AC=DF D.∠A=∠D
第2题图 第3题图 第4题图
3.如图,AD⊥BC于D,BD=DC,点E在AD上,则图中全等三角形共有 ( C )
A.1对 B.2对 C.3对 D.4对
4.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( B )
A.8 cm B.9 cm C.10 cm D.11 cm
5.如图,AB=CD,EC=FB,要使△EAC≌△FDB,需要添加下列选项中的( B )
A.AE∥DF B.CE∥BF C.∠A=∠D D.∠E=∠F
第5题图 第6题图 第7题图
6.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( B )
A.20° B.30° C.40° D.无法确定
7.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( C )
A.1对 B.2对 C.3对 D.4对
8.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( C )
A.∠BAD=∠CAE B.△ABD ≌△ACE
C.AB=BC D.BD=CE
第8题图 第9题图 第10题图
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( B )
A.150° B.180° C.210° D.225°
10.在△ABC中,AB=AC,求证:∠B=∠C.
证明:如图,作______.
在△ABD和△ACD中,
∴△ABD≌△ACD,
∴∠B=∠C.
其中,横线上应补充的条件是( C )
A.BC边上的高AD B.BC边上的中线AD C.∠A的平分线AD D.以上都不对
二、填空题
11.【2021·济宁】如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件______________________,使△ABC≌△ADC.
【答案】AD=AB(答案不唯一)
第11题图 第12题图 第13题图
12.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE= .
【答案】90°
13.如图,有一块三角形的镜子,马虎不小心将其打破成了1,2两块,现在需要配成同样大小的一块,为了方便起见,只要带上第___块,其理由是_______________ _____________________的两个三角形全等.
【答案】1 两边和它们的夹角对应相等
14.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)离地面的距离是50 cm,当小敏从水平位置CD下降30 cm时,这时小明离地面的高度是_____________.
【答案】80cm
第14题图 第15题图
15.观察下列结论:
(1)如图①,在正三角形ABC中,M,N是AB,BC上的点,且AM=BN,则AN___CM,∠NOC=______°;
(2)如图②,在正方形ABCD中,M,N是AB,BC上的点,且AM=BN,则AN___DM,∠NOD=______°;
(3)如图③,在正五边形ABCDE中,M,N是AB,BC上的点,且AM=BN,则AN___EM,∠NOE=_____°;
…
【答案】= 60 = 90 = 108
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于点O,也会有类似的结论,你的结论是________________________________.
【答案】A1N=AnM,∠NOAn=
三、解答题
16.【2021·大连】如图,点A,D,B,E在一条直线上,AD=BE,AC=DF,AC∥DF.求证:BC=EF.
证明:∵AD=BE,∴AD+BD=BE+BD,即AB=DE.
∵AC∥DF,∴∠A=∠EDF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).∴BC=EF.
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
18.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,
即∠COD=∠AOB.
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
19.如图,AB=AE,AD=AC,∠1=∠2.
(1)求证:BC=ED;
(2)若∠B=50°,求∠E的度数.
解:(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD.即∠CAB=∠DAE.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).∴BC=ED.
(2)由(1),得△ABC≌△AED,∴∠B=∠E.
∵∠B=50°,∴∠E=50°.
20.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于点F.
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
解:(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中,
∴△ACE≌△BCD,∴AE=BD.
(2)AE⊥BD.证明如下:
∵△ACE≌△BCD,∴∠EAC=∠FBE.
∵∠AEC=∠BEF,∴∠BFE=∠ACE=90°.
∴AE⊥BD.
21.如图,在△ABC中,AB>AC,AD是BC边上的中线.
求证:(AB-AC)<AD<(AB+AC).
【解析】本题可以运用倍长中线法构造全等三角形,利用全等三角形的性质,将三条线段转化到一个三角形中,然后利用三角形的三边关系来解决.涉及三角形中线问题时,常采用延长中线一倍的办法,可以将分居中线两旁的两条边集中于同一个三角形中,以利于问题的解决.
证明:如图,延长AD至点E,使DE=AD,连接BE.
则AE=2AD.
∵AD是BC边上的中线,∴CD=BD.
在△ACD和△EBD中,
∴△ACD≌△EBD(SAS). ∴AC=EB.
在△ABE中,AB-BE<AE即AB-AC<2AD
第2课时 运用“边角边”证三角形全等
【知识重点】
知识点 利用“SAS”判定三角形全等
1. 基本事实 两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2. 书写格式 如图,
在△ABC和△A′B′C′中 ,
∴△ABC≌△A′B′C′(SAS).
要点提醒
1. 相等的元素:两边及这两边的夹角.
2. 书写顺序:边→角→边.
特别解读
两边和其中一边的对角分别相等的两个三角形不一定全等.
【经典例题】
【例】如图,点C是AB的中点,AD=CE, 且AD∥ CE. 求证:△ACD≌△CBE.
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“SAS”判定两个三角形全等.
【同步练习】
一、选择题
1.下列三角形与△ABC全等的是( )
A.甲 B.乙 C.丙 D.甲和丙
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( )
A.BF=EC B.∠ACB=∠DFE C.AC=DF D.∠A=∠D
第2题图 第3题图 第4题图
3.如图,AD⊥BC于D,BD=DC,点E在AD上,则图中全等三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
4.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm B.9 cm C.10 cm D.11 cm
5.如图,AB=CD,EC=FB,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AE∥DF B.CE∥BF C.∠A=∠D D.∠E=∠F
第5题图 第6题图 第7题图
6.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( )
A.20° B.30° C.40° D.无法确定
7.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
A.∠BAD=∠CAE B.△ABD ≌△ACE
C.AB=BC D.BD=CE
第8题图 第9题图 第10题图
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.225°
10.在△ABC中,AB=AC,求证:∠B=∠C.
证明:如图,作______.
在△ABD和△ACD中,
∴△ABD≌△ACD,
∴∠B=∠C.
其中,横线上应补充的条件是( )
A.BC边上的高AD B.BC边上的中线AD
C.∠A的平分线AD D.以上都不对
二、填空题
11.【2021·济宁】如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件______________________,使△ABC≌△ADC.
第11题图 第12题图 第13题图
12.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE= .
13.如图,有一块三角形的镜子,马虎不小心将其打破成了1,2两块,现在需要配成同样大小的一块,为了方便起见,只要带上第___块,其理由是_______________ _____________________的两个三角形全等.
14.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)离地面的距离是50 cm,当小敏从水平位置CD下降30 cm时,这时小明离地面的高度是_____________.
15.观察下列结论:
(1)如图①,在正三角形ABC中,M,N是AB,BC上的点,且AM=BN,则AN___CM,∠NOC=______°;
(2)如图②,在正方形ABCD中,M,N是AB,BC上的点,且AM=BN,则AN___DM,∠NOD=______°;
(3)如图③,在正五边形ABCDE中,M,N是AB,BC上的点,且AM=BN,则AN___EM,∠NOE=_____°;
…
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于点O,也会有类似的结论,你的结论是________________________________.
第14题图 第15题图
三、解答题
16.【2021·大连】如图,点A,D,B,E在一条直线上,AD=BE,AC=DF,AC∥DF.求证:BC=EF.
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
18.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
19.如图,AB=AE,AD=AC,∠1=∠2.
(1)求证:BC=ED;
(2)若∠B=50°,求∠E的度数.
20.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于点F.
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
21.如图,在△ABC中,AB>AC,AD是BC边上的中线.
求证:(AB-AC)<AD<(AB+AC).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例】如图,点C是AB的中点,AD=CE, 且AD∥ CE. 求证:△ACD≌△CBE.
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“SAS”判定两个三角形全等.
证明:∵点C是AB的中点,∴ AC=CB.
∵ AD∥CE,∴∠CAD=∠BCE.
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
【同步练习】
一、选择题
1.下列三角形与△ABC全等的是( B )
A.甲 B.乙 C.丙 D.甲和丙
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF?( A )
A.BF=EC B.∠ACB=∠DFE C.AC=DF D.∠A=∠D
第2题图 第3题图 第4题图
3.如图,AD⊥BC于D,BD=DC,点E在AD上,则图中全等三角形共有 ( C )
A.1对 B.2对 C.3对 D.4对
4.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( B )
A.8 cm B.9 cm C.10 cm D.11 cm
5.如图,AB=CD,EC=FB,要使△EAC≌△FDB,需要添加下列选项中的( B )
A.AE∥DF B.CE∥BF C.∠A=∠D D.∠E=∠F
第5题图 第6题图 第7题图
6.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为( B )
A.20° B.30° C.40° D.无法确定
7.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( C )
A.1对 B.2对 C.3对 D.4对
8.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( C )
A.∠BAD=∠CAE B.△ABD ≌△ACE
C.AB=BC D.BD=CE
第8题图 第9题图 第10题图
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( B )
A.150° B.180° C.210° D.225°
10.在△ABC中,AB=AC,求证:∠B=∠C.
证明:如图,作______.
在△ABD和△ACD中,
∴△ABD≌△ACD,
∴∠B=∠C.
其中,横线上应补充的条件是( C )
A.BC边上的高AD B.BC边上的中线AD C.∠A的平分线AD D.以上都不对
二、填空题
11.【2021·济宁】如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件______________________,使△ABC≌△ADC.
【答案】AD=AB(答案不唯一)
第11题图 第12题图 第13题图
12.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE= .
【答案】90°
13.如图,有一块三角形的镜子,马虎不小心将其打破成了1,2两块,现在需要配成同样大小的一块,为了方便起见,只要带上第___块,其理由是_______________ _____________________的两个三角形全等.
【答案】1 两边和它们的夹角对应相等
14.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)离地面的距离是50 cm,当小敏从水平位置CD下降30 cm时,这时小明离地面的高度是_____________.
【答案】80cm
第14题图 第15题图
15.观察下列结论:
(1)如图①,在正三角形ABC中,M,N是AB,BC上的点,且AM=BN,则AN___CM,∠NOC=______°;
(2)如图②,在正方形ABCD中,M,N是AB,BC上的点,且AM=BN,则AN___DM,∠NOD=______°;
(3)如图③,在正五边形ABCDE中,M,N是AB,BC上的点,且AM=BN,则AN___EM,∠NOE=_____°;
…
【答案】= 60 = 90 = 108
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于点O,也会有类似的结论,你的结论是________________________________.
【答案】A1N=AnM,∠NOAn=
三、解答题
16.【2021·大连】如图,点A,D,B,E在一条直线上,AD=BE,AC=DF,AC∥DF.求证:BC=EF.
证明:∵AD=BE,∴AD+BD=BE+BD,即AB=DE.
∵AC∥DF,∴∠A=∠EDF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).∴BC=EF.
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
18.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,
即∠COD=∠AOB.
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
19.如图,AB=AE,AD=AC,∠1=∠2.
(1)求证:BC=ED;
(2)若∠B=50°,求∠E的度数.
解:(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD.即∠CAB=∠DAE.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).∴BC=ED.
(2)由(1),得△ABC≌△AED,∴∠B=∠E.
∵∠B=50°,∴∠E=50°.
20.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于点F.
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
解:(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中,
∴△ACE≌△BCD,∴AE=BD.
(2)AE⊥BD.证明如下:
∵△ACE≌△BCD,∴∠EAC=∠FBE.
∵∠AEC=∠BEF,∴∠BFE=∠ACE=90°.
∴AE⊥BD.
21.如图,在△ABC中,AB>AC,AD是BC边上的中线.
求证:(AB-AC)<AD<(AB+AC).
【解析】本题可以运用倍长中线法构造全等三角形,利用全等三角形的性质,将三条线段转化到一个三角形中,然后利用三角形的三边关系来解决.涉及三角形中线问题时,常采用延长中线一倍的办法,可以将分居中线两旁的两条边集中于同一个三角形中,以利于问题的解决.
证明:如图,延长AD至点E,使DE=AD,连接BE.
则AE=2AD.
∵AD是BC边上的中线,∴CD=BD.
在△ACD和△EBD中,
∴△ACD≌△EBD(SAS). ∴AC=EB.
在△ABE中,AB-BE<AE
