12.2.3运用“角边角”和“角角边”证三角形全等 同步练习(含答案)
文档属性
| 名称 | 12.2.3运用“角边角”和“角角边”证三角形全等 同步练习(含答案) | 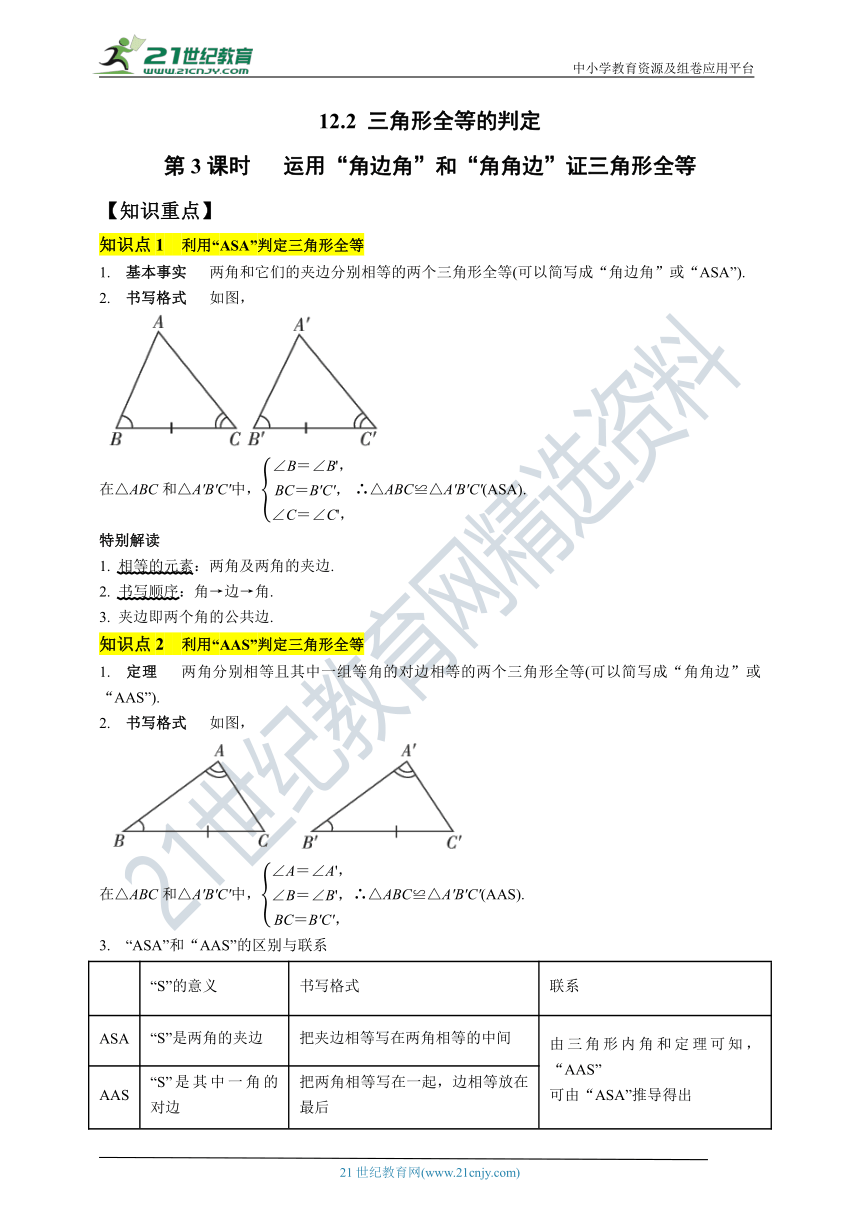 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 11:42:01 | ||
图片预览





文档简介
12.2 三角形全等的判定
第3课时 运用“角边角”和“角角边”证三角形全等
【知识重点】
知识点1 利用“ASA”判定三角形全等
1. 基本事实 两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2. 书写格式 如图,
在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(ASA).
特别解读
1. 相等的元素:两角及两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
知识点2 利用“AAS”判定三角形全等
1. 定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
2. 书写格式 如图,
在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS).
3. “ASA”和“AAS”的区别与联系
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“AAS” 可由“ASA”推导得出
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
特别解读
1. 判定两个三角形全等的三个条件中,“边”是必不可少的.
2. 在两个三角形的六个元素(三条边和三个角) 中,由已知的三个元素可判定两个三角形全等的组合有4 个:“SSS”“SAS” “ASA” 和“AAS”,不能判定两个三角形全等的组合是“AAA”和“SSA”(“ASS”).
【经典例题】
【例1】如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 求证:△ABC≌△DFE.
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
【例2】如图,已知AB=AC,AD=AE,求证:△BOD≌△COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
【同步练习】
一、选择题
1.如图,某同学把一块三角形的玻璃打碎成了3块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( )
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
第1题图 第2题图 第4题图
2.如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
A.∠BAD=∠CAD B.∠BAC=90° C.BD=AC D.∠B=45°
3.如图,能够判定全等的两个三角形是( )
A.①和② B.②和④ C.①和③ D.③和④
4.【2021·重庆】如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
5.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条件,使得能直接利用“ASA”判定△AOB≌△DOC,你补充的条件是( )
A.OA=OD B.OB=OC C.AB=CD D.OA=OC
第5题图 第6题图 第7题图
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
7.如图,BE=CD,AE=AD,∠1=∠2,∠2=100°,∠BAE=60°,则∠CAE为 ( )
A.20° B.30° C.40° D.50°
8.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的是( )
A.CD=DN B.∠1=∠2 C.BE=CF D.△ACN≌△ABM
第8题图 第9题图 第10题图
9.如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则此图中共有全等三角形的组数为( )
A.2 B.3 C.4 D.5
10.如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
11.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN ≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第11题图 第14题图 第15题图
二、填空题
12.两角及其________分别相等的两个三角形全等,简写成“________”或“________”.
13.______分别相等且其中一组______的______相等的两个三角形全等,简写成“________”或“________”.
14.如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是_____________________.
15.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,可先证△AEB ≌△AEC,根据是 ,再证△BDE ≌△ ,根据是: .
16.如图,∠A=∠D,∠ACB=∠DBC,若BC=4,△AOB的周长为10,则△DCB的周长为 .
第16题图 第17题图
17.如图,在平面直角坐标系中,四边形OBCD是正方形,B点的坐标为(2,1),则C点的坐标为 .
三、解答题
18.如图,AB=AE, ∠1=∠2,∠C=∠D. 求证:△ABC≌△AED.
19.如图,在△ABE和△CDF中,点C,E,F,B在同一直线上,BF=CE.若AE∥FD,∠A=∠D.求证:AB=DC.
20.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
21.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
22.CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α,若直线CD经过∠BCA的内部,且E,F在射线C,D上,请解答下面的两个问题:
(1)如图①,若∠BCA=90°,∠α=90°,则BE___CF,EF___|BE-AF|(填“>”“<”或“=”);
(2)如图②,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件:______________________,使(1)中的两个结论仍然成立,并证明两个结论成立;
(3)拓展应用:如图③,在△ABC中,AB=AC,AB>BC.点D在BC边上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,则△ACF与△BDE的面积之和是___.
23.(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易说明△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断. AB,AD,DC之间的等量关系是______________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并说明你的结论.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 求证:△ABC≌△DFE.
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
证明:∵ AB∥DF,且点B,E,C,F在一条直线上,
∴∠B=∠F.
∵ AC∥DE,∴∠ACB=∠DEF.
在△ABC和△DFE中,
∴△ABC≌△DFE(ASA).
【例2】如图,已知AB=AC,AD=AE,求证:△BOD≌△COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS). ∴∠B=∠C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△BOD和△COE中,
∴△BOD ≌△COE(AAS).
【同步练习】
一、选择题
1.如图,某同学把一块三角形的玻璃打碎成了3块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( C )
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
第1题图 第2题图 第4题图
2.如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( A )
A.∠BAD=∠CAD B.∠BAC=90° C.BD=AC D.∠B=45°
3.如图,能够判定全等的两个三角形是( D )
A.①和② B.②和④ C.①和③ D.③和④
4.【2021·重庆】如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是( C )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
5.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条件,使得能直接利用“ASA”判定△AOB≌△DOC,你补充的条件是( A )
A.OA=OD B.OB=OC C.AB=CD D.OA=OC
第5题图 第6题图 第7题图
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( B )
A.0.5 B.1 C.1.5 D.2
7.如图,BE=CD,AE=AD,∠1=∠2,∠2=100°,∠BAE=60°,则∠CAE为 ( C )
A.20° B.30° C.40° D.50°
8.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的是( A )
A.CD=DN B.∠1=∠2 C.BE=CF D.△ACN≌△ABM
第8题图 第9题图 第10题图
9.如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则此图中共有全等三角形的组数为( C )
A.2 B.3 C.4 D.5
10.如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( D )
A.a+c B.b+c C.a-b+c D.a+b-c
11.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN ≌△ABM.其中正确的有 ( C )
A.1个 B.2个 C.3个 D.4个
第11题图 第14题图 第15题图
二、填空题
12.两角及其________分别相等的两个三角形全等,简写成“________”或“________”.
【答案】夹角 ASA 角边角
13.______分别相等且其中一组______的______相等的两个三角形全等,简写成“________”或“________”.
【答案】两角 等角 对边 角角边 AAS
14.如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是_____________________.
【答案】AC=BC(答案不唯一)
15.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,可先证△AEB ≌△AEC,根据是 ,再证△BDE ≌△ ,根据是: .
【答案】ASA或AAS CDE SAS
16.如图,∠A=∠D,∠ACB=∠DBC,若BC=4,△AOB的周长为10,则△DCB的周长为 .
【答案】14
第16题图 第17题图
17.如图,在平面直角坐标系中,四边形OBCD是正方形,B点的坐标为(2,1),则C点的坐标为 .
【答案】(1,3)
三、解答题
18.如图,AB=AE, ∠1=∠2,∠C=∠D. 求证:△ABC≌△AED.
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
在△ABC和△AED中,
∴△ABC≌△AED(AAS).
19.如图,在△ABE和△CDF中,点C,E,F,B在同一直线上,BF=CE.若AE∥FD,∠A=∠D.求证:AB=DC.
证明:∵AE∥FD,
∴∠AEB=∠DFC.
∵BF=CE,
∴BF+EF=CE+EF,
∴BE=CF.
在△ABE和△DCF中,
∴△ABE≌△DCF(AAS),∴AB=DC.
20.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
解:∵AB∥CD,∴∠ABO=∠CDO.
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即OB⊥AB.
∵相邻两平行线间的距离相等,∴OD=OB,
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA),∴CD=AB=20(米).
21.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
解:(1)证明:∵CB为∠ACE的平分线,
∴∠BCA=∠ECF.
在△ABC和△FEC中,
∴△ABC≌△FEC.∴AB=FE.
(2)∵AB∥CE,∴∠B=∠ECF.
∴∠B=∠E=∠BCA=∠ECF.
∵ED⊥AC,∴∠E+∠BCA+∠ECF=90°.
∴∠B=∠E=∠BCA=∠ECF=30°.
∴∠A=180°-∠B-∠BCA=120°.
22.CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α,若直线CD经过∠BCA的内部,且E,F在射线C,D上,请解答下面的两个问题:
(1)如图①,若∠BCA=90°,∠α=90°,则BE___CF,EF___|BE-AF|(填“>”“<”或“=”);
【答案】= =
(2)如图②,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件:______________________,使(1)中的两个结论仍然成立,并证明两个结论成立;
【答案】∠α+∠BCA=180°
解:(2)在图②中,∵∠CFA+∠BCA=180°,
∴∠CFA+∠BCE+∠ACF=180°.
∵∠CFA+∠ACF+∠CAF=180°,
∴∠BCE=∠CAF.
在△BCE和△CAF中,
∴△BCE≌△CAF,∴BE=CF,CE=AF,
∴EF=|CF-CE|=|BE-AF|.
(3)拓展应用:如图③,在△ABC中,AB=AC,AB>BC.点D在BC边上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,则△ACF与△BDE的面积之和是___.
【答案】6
23.(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易说明△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断. AB,AD,DC之间的等量关系是______________;
【答案】AD=AB+DC
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并说明你的结论.
【解析】延长AE交DF的延长线于点G,由“AAS”说明△AEB≌△GEC,可得AB=CG,再利用平行线的性质与角平分线的定义可得∠FAG=∠G,进而可得结论.
解:AB=CF+AF.
如图,延长AE交DF的延长线于点G.
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠G.
又∵∠AEB=∠GEC,∴△AEB≌△GEC(AAS).∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAG=∠G,∴∠FAG=∠G.
过点F作AG的垂线,垂足为H,则∠FHA=∠FHG=90°,
又∵FH=FH,∠FAG=∠G,
∴△FHA≌△FHG.∴AF=GF.
∵CG=CF+GF,∴AB=CF+AF.
第3课时 运用“角边角”和“角角边”证三角形全等
【知识重点】
知识点1 利用“ASA”判定三角形全等
1. 基本事实 两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2. 书写格式 如图,
在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(ASA).
特别解读
1. 相等的元素:两角及两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
知识点2 利用“AAS”判定三角形全等
1. 定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
2. 书写格式 如图,
在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS).
3. “ASA”和“AAS”的区别与联系
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“AAS” 可由“ASA”推导得出
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
特别解读
1. 判定两个三角形全等的三个条件中,“边”是必不可少的.
2. 在两个三角形的六个元素(三条边和三个角) 中,由已知的三个元素可判定两个三角形全等的组合有4 个:“SSS”“SAS” “ASA” 和“AAS”,不能判定两个三角形全等的组合是“AAA”和“SSA”(“ASS”).
【经典例题】
【例1】如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 求证:△ABC≌△DFE.
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
【例2】如图,已知AB=AC,AD=AE,求证:△BOD≌△COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
【同步练习】
一、选择题
1.如图,某同学把一块三角形的玻璃打碎成了3块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( )
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
第1题图 第2题图 第4题图
2.如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
A.∠BAD=∠CAD B.∠BAC=90° C.BD=AC D.∠B=45°
3.如图,能够判定全等的两个三角形是( )
A.①和② B.②和④ C.①和③ D.③和④
4.【2021·重庆】如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
5.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条件,使得能直接利用“ASA”判定△AOB≌△DOC,你补充的条件是( )
A.OA=OD B.OB=OC C.AB=CD D.OA=OC
第5题图 第6题图 第7题图
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
7.如图,BE=CD,AE=AD,∠1=∠2,∠2=100°,∠BAE=60°,则∠CAE为 ( )
A.20° B.30° C.40° D.50°
8.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的是( )
A.CD=DN B.∠1=∠2 C.BE=CF D.△ACN≌△ABM
第8题图 第9题图 第10题图
9.如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则此图中共有全等三角形的组数为( )
A.2 B.3 C.4 D.5
10.如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
11.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN ≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第11题图 第14题图 第15题图
二、填空题
12.两角及其________分别相等的两个三角形全等,简写成“________”或“________”.
13.______分别相等且其中一组______的______相等的两个三角形全等,简写成“________”或“________”.
14.如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是_____________________.
15.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,可先证△AEB ≌△AEC,根据是 ,再证△BDE ≌△ ,根据是: .
16.如图,∠A=∠D,∠ACB=∠DBC,若BC=4,△AOB的周长为10,则△DCB的周长为 .
第16题图 第17题图
17.如图,在平面直角坐标系中,四边形OBCD是正方形,B点的坐标为(2,1),则C点的坐标为 .
三、解答题
18.如图,AB=AE, ∠1=∠2,∠C=∠D. 求证:△ABC≌△AED.
19.如图,在△ABE和△CDF中,点C,E,F,B在同一直线上,BF=CE.若AE∥FD,∠A=∠D.求证:AB=DC.
20.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
21.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
22.CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α,若直线CD经过∠BCA的内部,且E,F在射线C,D上,请解答下面的两个问题:
(1)如图①,若∠BCA=90°,∠α=90°,则BE___CF,EF___|BE-AF|(填“>”“<”或“=”);
(2)如图②,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件:______________________,使(1)中的两个结论仍然成立,并证明两个结论成立;
(3)拓展应用:如图③,在△ABC中,AB=AC,AB>BC.点D在BC边上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,则△ACF与△BDE的面积之和是___.
23.(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易说明△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断. AB,AD,DC之间的等量关系是______________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并说明你的结论.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 求证:△ABC≌△DFE.
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
证明:∵ AB∥DF,且点B,E,C,F在一条直线上,
∴∠B=∠F.
∵ AC∥DE,∴∠ACB=∠DEF.
在△ABC和△DFE中,
∴△ABC≌△DFE(ASA).
【例2】如图,已知AB=AC,AD=AE,求证:△BOD≌△COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS). ∴∠B=∠C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△BOD和△COE中,
∴△BOD ≌△COE(AAS).
【同步练习】
一、选择题
1.如图,某同学把一块三角形的玻璃打碎成了3块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( C )
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
第1题图 第2题图 第4题图
2.如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( A )
A.∠BAD=∠CAD B.∠BAC=90° C.BD=AC D.∠B=45°
3.如图,能够判定全等的两个三角形是( D )
A.①和② B.②和④ C.①和③ D.③和④
4.【2021·重庆】如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是( C )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
5.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条件,使得能直接利用“ASA”判定△AOB≌△DOC,你补充的条件是( A )
A.OA=OD B.OB=OC C.AB=CD D.OA=OC
第5题图 第6题图 第7题图
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( B )
A.0.5 B.1 C.1.5 D.2
7.如图,BE=CD,AE=AD,∠1=∠2,∠2=100°,∠BAE=60°,则∠CAE为 ( C )
A.20° B.30° C.40° D.50°
8.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的是( A )
A.CD=DN B.∠1=∠2 C.BE=CF D.△ACN≌△ABM
第8题图 第9题图 第10题图
9.如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则此图中共有全等三角形的组数为( C )
A.2 B.3 C.4 D.5
10.如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( D )
A.a+c B.b+c C.a-b+c D.a+b-c
11.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN ≌△ABM.其中正确的有 ( C )
A.1个 B.2个 C.3个 D.4个
第11题图 第14题图 第15题图
二、填空题
12.两角及其________分别相等的两个三角形全等,简写成“________”或“________”.
【答案】夹角 ASA 角边角
13.______分别相等且其中一组______的______相等的两个三角形全等,简写成“________”或“________”.
【答案】两角 等角 对边 角角边 AAS
14.如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是_____________________.
【答案】AC=BC(答案不唯一)
15.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,可先证△AEB ≌△AEC,根据是 ,再证△BDE ≌△ ,根据是: .
【答案】ASA或AAS CDE SAS
16.如图,∠A=∠D,∠ACB=∠DBC,若BC=4,△AOB的周长为10,则△DCB的周长为 .
【答案】14
第16题图 第17题图
17.如图,在平面直角坐标系中,四边形OBCD是正方形,B点的坐标为(2,1),则C点的坐标为 .
【答案】(1,3)
三、解答题
18.如图,AB=AE, ∠1=∠2,∠C=∠D. 求证:△ABC≌△AED.
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
在△ABC和△AED中,
∴△ABC≌△AED(AAS).
19.如图,在△ABE和△CDF中,点C,E,F,B在同一直线上,BF=CE.若AE∥FD,∠A=∠D.求证:AB=DC.
证明:∵AE∥FD,
∴∠AEB=∠DFC.
∵BF=CE,
∴BF+EF=CE+EF,
∴BE=CF.
在△ABE和△DCF中,
∴△ABE≌△DCF(AAS),∴AB=DC.
20.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
解:∵AB∥CD,∴∠ABO=∠CDO.
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即OB⊥AB.
∵相邻两平行线间的距离相等,∴OD=OB,
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA),∴CD=AB=20(米).
21.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
解:(1)证明:∵CB为∠ACE的平分线,
∴∠BCA=∠ECF.
在△ABC和△FEC中,
∴△ABC≌△FEC.∴AB=FE.
(2)∵AB∥CE,∴∠B=∠ECF.
∴∠B=∠E=∠BCA=∠ECF.
∵ED⊥AC,∴∠E+∠BCA+∠ECF=90°.
∴∠B=∠E=∠BCA=∠ECF=30°.
∴∠A=180°-∠B-∠BCA=120°.
22.CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α,若直线CD经过∠BCA的内部,且E,F在射线C,D上,请解答下面的两个问题:
(1)如图①,若∠BCA=90°,∠α=90°,则BE___CF,EF___|BE-AF|(填“>”“<”或“=”);
【答案】= =
(2)如图②,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件:______________________,使(1)中的两个结论仍然成立,并证明两个结论成立;
【答案】∠α+∠BCA=180°
解:(2)在图②中,∵∠CFA+∠BCA=180°,
∴∠CFA+∠BCE+∠ACF=180°.
∵∠CFA+∠ACF+∠CAF=180°,
∴∠BCE=∠CAF.
在△BCE和△CAF中,
∴△BCE≌△CAF,∴BE=CF,CE=AF,
∴EF=|CF-CE|=|BE-AF|.
(3)拓展应用:如图③,在△ABC中,AB=AC,AB>BC.点D在BC边上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,则△ACF与△BDE的面积之和是___.
【答案】6
23.(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易说明△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断. AB,AD,DC之间的等量关系是______________;
【答案】AD=AB+DC
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并说明你的结论.
【解析】延长AE交DF的延长线于点G,由“AAS”说明△AEB≌△GEC,可得AB=CG,再利用平行线的性质与角平分线的定义可得∠FAG=∠G,进而可得结论.
解:AB=CF+AF.
如图,延长AE交DF的延长线于点G.
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠G.
又∵∠AEB=∠GEC,∴△AEB≌△GEC(AAS).∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAG=∠G,∴∠FAG=∠G.
过点F作AG的垂线,垂足为H,则∠FHA=∠FHG=90°,
又∵FH=FH,∠FAG=∠G,
∴△FHA≌△FHG.∴AF=GF.
∵CG=CF+GF,∴AB=CF+AF.
