相似三角形
图片预览


文档简介
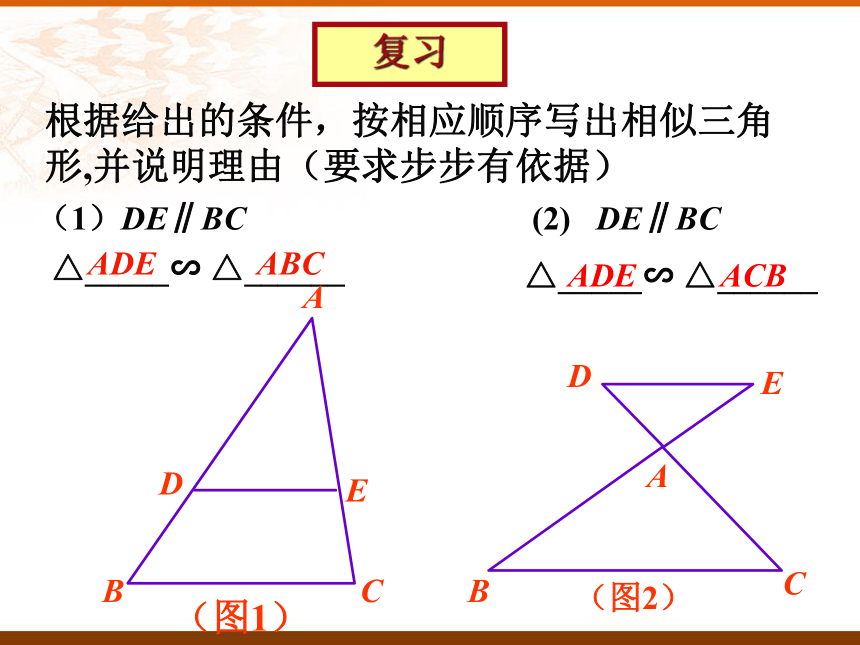
课件19张PPT。九年级备课组三角形相似的判定根据给出的条件,按相应顺序写出相似三角形,并说明理由(要求步步有依据)(2) DE∥BC
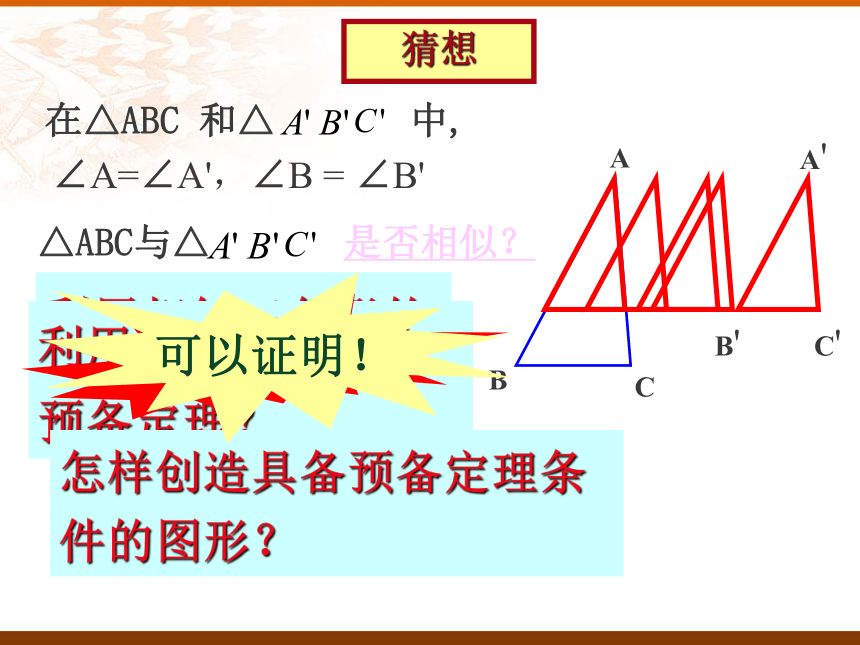
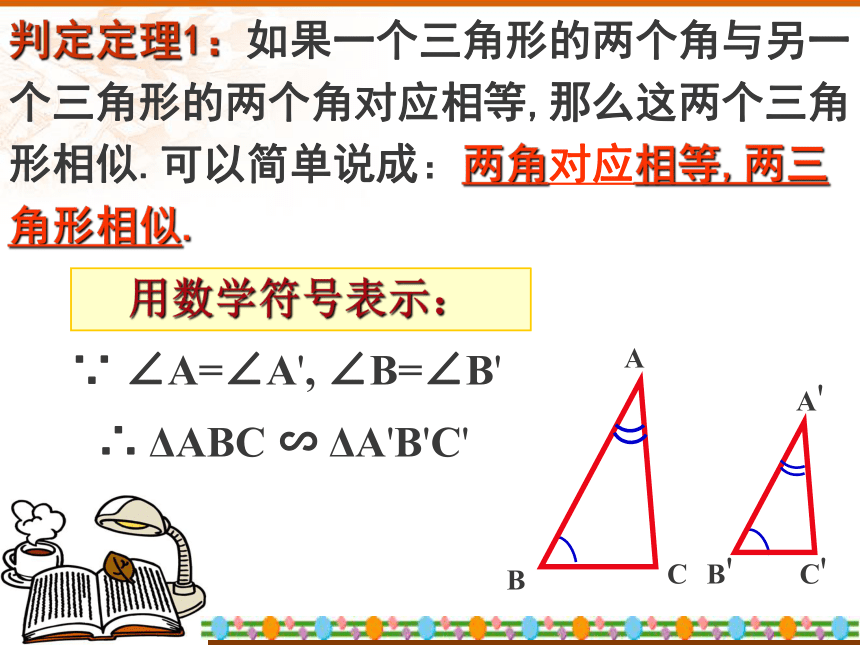
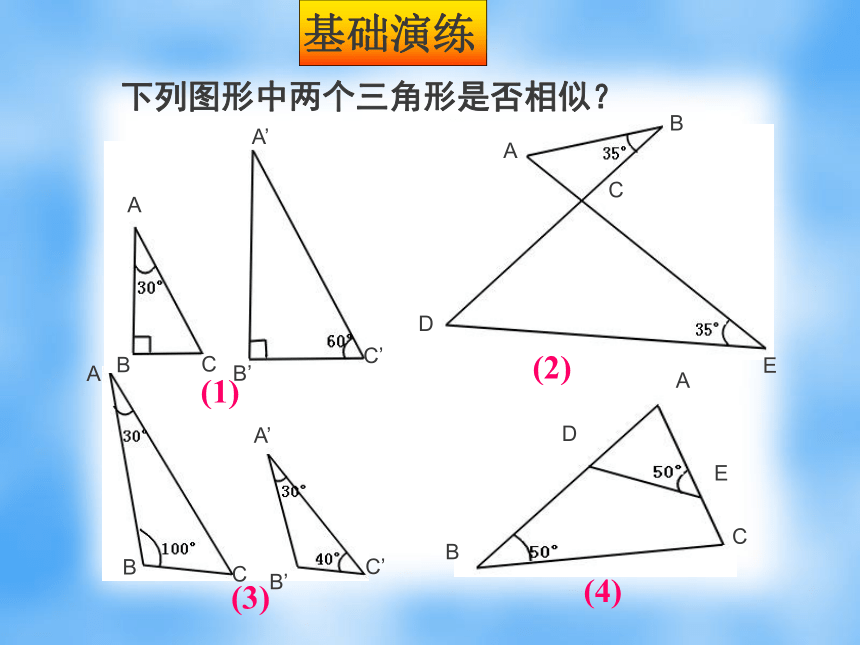
△_____∽ △______ △_____∽ △______ (1)DE∥BC ADE ABCADE ACB复习在△ABC 和△ 中,△ABC与△ 是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!猜想∠A=∠A',∠B = ∠B'ABCA/ C/ B/ ∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可以简单说成:两角对应相等,两三角形相似.∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:下列图形中两个三角形是否相似?(1)(2)(3)(4)如图所示,∠B=∠C,尝试找出
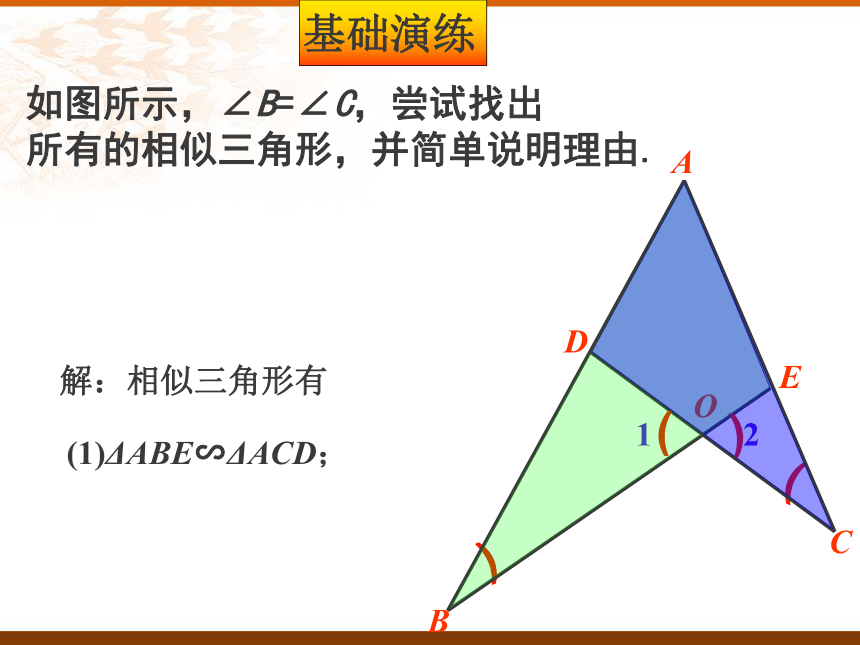
所有的相似三角形,并简单说明理由.解:相似三角形有(1)ΔABE∽ΔACD;如图所示,∠B=∠C,尝试找出
所有的相似三角形,并简单说明理由.解:相似三角形有(1)ΔABE∽ΔACD;(2)ΔBOD∽ΔCOE; (1)所有的等腰三角形都相似。( )
(2)所有的等腰直角三角形都相似。( )
(3)所有的等边三角形都相似。( )
(4)所有的直角三角形都相似。( )判断下列说法是否正确?并说明理由。 (5)有一个角是100 °的两个等腰三角形都相似。( )
(6)有一个角是70 °的两个等腰三角形都相似。 ( ) (1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?(2)已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/。
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/。1.如图(1), AE与BD交于点C, 要使△ABC∽△DEC,
需要条件________________.2.如图(2), 要使△ABC∽△ACD,
需要条件________________.3.如图(3), 要使△ABE∽△ACD,
需要条件________________.例题解析:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACDC ADB已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.)))))2 1 证明:(两角对应相等,两三角形相似)⑴∵DE∥BC, EF∥AB
∴∠1=∠C,∠2=∠A.
∴△ADE∽△EFC;如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.)))))2 1 证明:⑴另解:
∵DE∥BC, EF∥AB
∴△ADE∽△ABC,△EFC∽△ABC;
∴△ADE∽△EFC;如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.证明:⑵∵△ADE∽△EFC, ∴AE·EF=AD·EC. ∴图中共有几对相似三角形? 过△ABC(∠C>∠B)的边AB上一点D作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?请把它们一一作出来。这样的直线有几条?ABCD ●AB小结相似三角形的判定方法? 相似三角形的定义? 相似三角形的判定定理1? 相似三角形判定的预备定理 ? 母子相似定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。看已知条件识别相似选方法找出识别方法中所需的条件
△_____∽ △______ △_____∽ △______ (1)DE∥BC ADE ABCADE ACB复习在△ABC 和△ 中,△ABC与△ 是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!猜想∠A=∠A',∠B = ∠B'ABCA/ C/ B/ ∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可以简单说成:两角对应相等,两三角形相似.∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:下列图形中两个三角形是否相似?(1)(2)(3)(4)如图所示,∠B=∠C,尝试找出
所有的相似三角形,并简单说明理由.解:相似三角形有(1)ΔABE∽ΔACD;如图所示,∠B=∠C,尝试找出
所有的相似三角形,并简单说明理由.解:相似三角形有(1)ΔABE∽ΔACD;(2)ΔBOD∽ΔCOE; (1)所有的等腰三角形都相似。( )
(2)所有的等腰直角三角形都相似。( )
(3)所有的等边三角形都相似。( )
(4)所有的直角三角形都相似。( )判断下列说法是否正确?并说明理由。 (5)有一个角是100 °的两个等腰三角形都相似。( )
(6)有一个角是70 °的两个等腰三角形都相似。 ( ) (1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?(2)已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/。
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/。1.如图(1), AE与BD交于点C, 要使△ABC∽△DEC,
需要条件________________.2.如图(2), 要使△ABC∽△ACD,
需要条件________________.3.如图(3), 要使△ABE∽△ACD,
需要条件________________.例题解析:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:如图, Rt△ABC中,CD是斜边的高.求证:△ABC ∽ △CBD ∽ △ACDC ADB已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.)))))2 1 证明:(两角对应相等,两三角形相似)⑴∵DE∥BC, EF∥AB
∴∠1=∠C,∠2=∠A.
∴△ADE∽△EFC;如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.)))))2 1 证明:⑴另解:
∵DE∥BC, EF∥AB
∴△ADE∽△ABC,△EFC∽△ABC;
∴△ADE∽△EFC;如图,△ABC中,
DE∥BC,EF∥AB,
求证:⑴△ADE∽△EFC;
⑵AE?EF=AD?EC.证明:⑵∵△ADE∽△EFC, ∴AE·EF=AD·EC. ∴图中共有几对相似三角形? 过△ABC(∠C>∠B)的边AB上一点D作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?请把它们一一作出来。这样的直线有几条?ABCD ●AB小结相似三角形的判定方法? 相似三角形的定义? 相似三角形的判定定理1? 相似三角形判定的预备定理 ? 母子相似定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。看已知条件识别相似选方法找出识别方法中所需的条件
