四川省绵阳市重点中学2023-2024学年高一上学期新生入学考试数学试题(含答案)
文档属性
| 名称 | 四川省绵阳市重点中学2023-2024学年高一上学期新生入学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 767.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 19:40:23 | ||
图片预览




文档简介
绵阳市重点中学2023-2024学年高一上学期新生入学考试
数学试卷题
本测评题分试题卷和答题卷两部份,试题卷共5页,满分150分,时间120分钟.
注意事项:
1.答题前,请将本人的信息用0.5毫米的黑色墨水签字笔或黑色墨水钢笔填在答题卡的对应位置上;
2.选择题的答案,必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑;
3.请用0.5毫米的黑色墨水签字笔或黑色墨水钢笔将每个题目的答案答在答题卷上每题对应的位置上,答在试题卷上的无效.作图一律用2B铅笔或0.5毫米黑色签字笔;
第Ⅰ卷(选择题,共36分)
一、选择题:本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合题目要求的.
1.的平方根为( )
A.±3 B.±9 C.3 D.3
2.下列各式,运算正确的是( )
A. B.
C. D.
3.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记数字6对面的数字为,数字2对面的数字为,那么的值为( )
A.3 B.7 C.8 D.11
4.点,在反比例函数的图象上,且,则( )
A. B.
C. D.
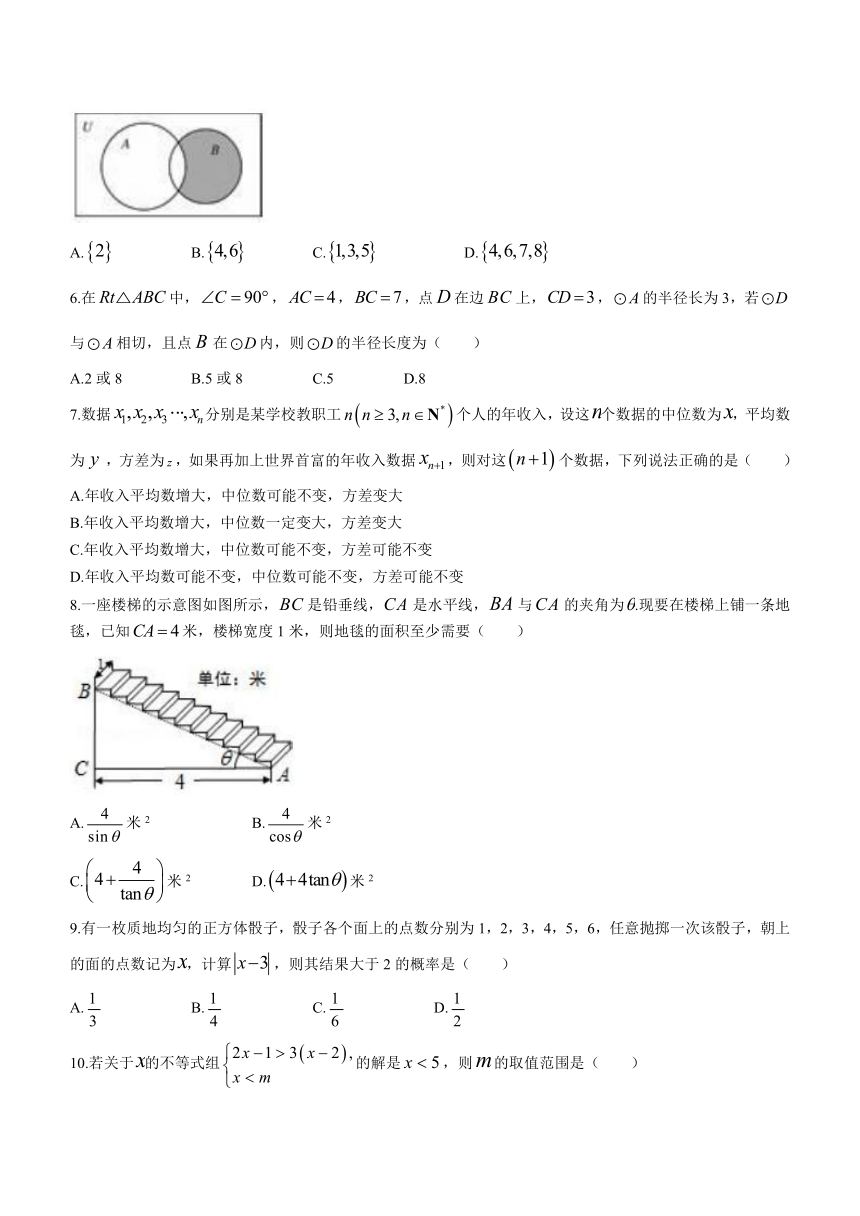
5.设全集,集合,,则图中的阴影部分表示的集合为( )
A. B. C. D.
6.在中,,,,点在边上,,的半径长为3,若与相切,且点在内,则的半径长度为( )
A.2或8 B.5或8 C.5 D.8
7.数据分别是某学校教职工个人的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上世界首富的年收入数据,则对这个数据,下列说法正确的是( )
A.年收入平均数增大,中位数可能不变,方差变大
B.年收入平均数增大,中位数一定变大,方差变大
C.年收入平均数增大,中位数可能不变,方差可能不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
8.一座楼梯的示意图如图所示,是铅垂线,是水平线,与的夹角为.现要在楼梯上铺一条地毯,已知米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2
C.米2 D.米2
9.有一枚质地均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,任意抛掷一次该骰子,朝上的面的点数记为,计算,则其结果大于2的概率是( )
A. B. C. D.
10.若关于的不等式组的解是,则的取值范围是( )
A. B. C. D.
11.已知集合,则满足条件的集合的个数为( )
A.3 B.4 C.7 D.8
12.对于每个非零自然数,抛物线与轴交于、两点,以表示这两点间的距离,则的值是( )
A. B. C. D.
第Ⅱ卷(非选择题,共114分)
二、填空题:本大题共6小题,每小题4分,共24分.请将答案填写在答题卷中的横线上.
13.已知对任意的,,都有则的值为__________.
14.底面圆半径为6cm,高为8cm的圆锥,其侧面展开扇形圆心角的度数为__________.
15.已知,,若集合,则的值为__________.
16.若,则的值为__________.
17.如果关于的分式方程无解,则的值为__________.
18.对于正数,规定,计算__________.
三、解答题:共7小题,满分90分.解答应写出必要的文字说明、证明过程或演算步骤.
19.(本题满分16分)
(1)计算:
(2)先化简,再求值:,其中.
20.(本题满分12分)
某校为庆祝中华人民共和国建国70周年,以“不忘初心,牢记使命”为主题开展了“唱红歌”比赛,工作人员根据参赛选手的成绩绘制了如下不完整的统计图表:
分数段 频数 频率
0.15
0.45
60
请根据以上图表提供的信息,解答下列问题:
(1)求上表中的数据,的值;
(2)通过计算,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)如果比赛成绩在80分以上(含80分)的选手为获奖选手,那么我们随机的从本次参赛的所有选手中抽取出一个人,求恰好抽中获奖选手的概率?
21.(本题满分12分)
已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求的值;
(2)求证:.
22.(本题满分12分)
为实现区域教育均衡发展,我市计划对某县、两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所类学校和两所类学校共需资金230万元;改造两所类学校和一所类学校共需资金205万元.
(1)改造一所类学校和一所类学校所需的资金分别是多少万元?
(2)若该县的类学校不超过5所,则类学校至少有多少所?
(3)我市计划今年对该县、两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到、两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
23.(本题满分12分)
如图,内接于半圆,是直径,过作直线使.是弧的中点,交于,于,交于.
(1)求证:是半圆的切线;
(2)求证:.
(3)若的面积为4.5,且,,求的面积.
24.(本题满分12分)
如图,抛物线与轴交于点,与轴交于、两点,点在点左侧.点的坐标为,.
(1)求抛物线的解析式;
(2)若点是线段下方抛物线上的动点,求四边形面积的最大值;
(3)若点在轴上,点在抛物线上.是否存在以、、、为顶点且以为一边的平行四边形 若存在,求点的坐标;若不存在,请说明理由.
25.(本题满分14分)
如图1,已知直线与轴、轴分别交于点和点,过直线上的两点、分别作轴的垂线段,垂足分别为和,其中,.
(1)如果,,试判断的形状;
(2)如果,(1)中有关的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;
(3)如图2,题目中的条件不变,如果,并且,求经过、、三点的抛物线所对应的函数关系式;
(4)在(3)的条件下,如果抛物线的对称轴与线段交于点,点是对称轴上一动点,以点、、为顶点的三角形和以点、、为顶点的三角形相似,求符合条件的点的坐标.
绵阳市重点中学2023-2024学年高一上学期新生入学考试
数学试卷
参考答案及评分标准
一、选择题(每个小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A C B A B D A D C B D C
二、填空题(每个小题4分,共24分)
13. 14.216° 15.-1 16.18 17.5或2 18.2022.5
三、解答:(共90分)
19.解(1)原式
(2)原式
把代入得原式.
20.解(1)∵总人数(人)
∴,.
(2)由(1)的计算知70至80分段的人数为90人,
90至100分段的人数人,
补全条形图如下图所示:
(3)比赛成绩的中位数落在:70~80分.
(4)恰好抽中获奖选手的概率为:.
21.解(1)由,解得,所以
,.
在中,,,
∴.
(2)取点关于原点的对称点,则问题转化为求证.
由勾股定理可得,,,,
∵,
∴是等腰直角三角形.∴.∴.
22.解(1)设改造一所类学校和一所类学校所需的改造资金分别为万元和万元.
依题意得:
解之得
答:改造一所类学校和一所类学校所需的改造资金分别为60万元和85万元.
(2)设该县有、两类学校分别为所和所.
则
∵类学校不超过5所∴∴.
即:类学校至少有15所.
(3)设今年改造类学校所,则改造类学校为所,
依题意得:
解之得.
∵取整数∴
即:共有4种方案.
23.证明(1):∵是直径∴,
∵∴,即
∴是半圆的切线.
(2)如图
∵是弧的中点,∴
∵是直径∴,故
∵,∴,
∴,∴.
(3)连结则,
∵,是弧的中点∴
∴,∴.
又∵,
∴
∴
∴.
(其它解法,请酌情评分)
24.解(1)∵点,,
把、代入得:
解得:,
∴所求抛物线的解析式为.
(2)过点作轴分别交线段和轴于点、.
∵对称轴,,∴点
∴
易得直线的解析式为
令,,其中,
当时,有最大值3
此时四边形面积有最大值.
(3)如图,有如下情况:
①过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形,
∵,
令得:,
∴点,
②平移直线交轴于点,交轴上方的抛物线于点,当时,四边形为平行四边形,
∵,∴由对称关系令,由
化简得:,解得或,
此时存在点和
综上,存在3个点符合题意,坐标分别是,,.
25.(1)是直角三角形.
依题意得,,,∴
在中,
在中,
∴
∴是直角三角形(解法不惟一).
(2)答:(1)中的结论还成立.
依题意得,,
∴
∴
∵∴
又∵在中,
在中,
∴
∴
∴是直角三角形.(解法不惟一).
(3)∵,,∴.
方法一:设抛物线的函数关系式为.
∵抛物线经过点、和
∴,∴
∴所求抛物线的函数关系式为.
方法二:设抛物线的函数关系式为.
∵抛物线经过点∴解得
∴所求抛物线的函数关系式为
即.
(4)抛物线的对称轴与轴的交点符合条件,
∵,,∴
∵抛物线的对称轴为,∴
∴.
过点作,交抛物线的对称轴于点.
∴、、和两两相似
∴即.
∵点位于第四象限,∴.
因此,符合条件的点有两个,分别是,.
(解法不惟一)
数学试卷题
本测评题分试题卷和答题卷两部份,试题卷共5页,满分150分,时间120分钟.
注意事项:
1.答题前,请将本人的信息用0.5毫米的黑色墨水签字笔或黑色墨水钢笔填在答题卡的对应位置上;
2.选择题的答案,必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑;
3.请用0.5毫米的黑色墨水签字笔或黑色墨水钢笔将每个题目的答案答在答题卷上每题对应的位置上,答在试题卷上的无效.作图一律用2B铅笔或0.5毫米黑色签字笔;
第Ⅰ卷(选择题,共36分)
一、选择题:本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合题目要求的.
1.的平方根为( )
A.±3 B.±9 C.3 D.3
2.下列各式,运算正确的是( )
A. B.
C. D.
3.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记数字6对面的数字为,数字2对面的数字为,那么的值为( )
A.3 B.7 C.8 D.11
4.点,在反比例函数的图象上,且,则( )
A. B.
C. D.
5.设全集,集合,,则图中的阴影部分表示的集合为( )
A. B. C. D.
6.在中,,,,点在边上,,的半径长为3,若与相切,且点在内,则的半径长度为( )
A.2或8 B.5或8 C.5 D.8
7.数据分别是某学校教职工个人的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上世界首富的年收入数据,则对这个数据,下列说法正确的是( )
A.年收入平均数增大,中位数可能不变,方差变大
B.年收入平均数增大,中位数一定变大,方差变大
C.年收入平均数增大,中位数可能不变,方差可能不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
8.一座楼梯的示意图如图所示,是铅垂线,是水平线,与的夹角为.现要在楼梯上铺一条地毯,已知米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2
C.米2 D.米2
9.有一枚质地均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,任意抛掷一次该骰子,朝上的面的点数记为,计算,则其结果大于2的概率是( )
A. B. C. D.
10.若关于的不等式组的解是,则的取值范围是( )
A. B. C. D.
11.已知集合,则满足条件的集合的个数为( )
A.3 B.4 C.7 D.8
12.对于每个非零自然数,抛物线与轴交于、两点,以表示这两点间的距离,则的值是( )
A. B. C. D.
第Ⅱ卷(非选择题,共114分)
二、填空题:本大题共6小题,每小题4分,共24分.请将答案填写在答题卷中的横线上.
13.已知对任意的,,都有则的值为__________.
14.底面圆半径为6cm,高为8cm的圆锥,其侧面展开扇形圆心角的度数为__________.
15.已知,,若集合,则的值为__________.
16.若,则的值为__________.
17.如果关于的分式方程无解,则的值为__________.
18.对于正数,规定,计算__________.
三、解答题:共7小题,满分90分.解答应写出必要的文字说明、证明过程或演算步骤.
19.(本题满分16分)
(1)计算:
(2)先化简,再求值:,其中.
20.(本题满分12分)
某校为庆祝中华人民共和国建国70周年,以“不忘初心,牢记使命”为主题开展了“唱红歌”比赛,工作人员根据参赛选手的成绩绘制了如下不完整的统计图表:
分数段 频数 频率
0.15
0.45
60
请根据以上图表提供的信息,解答下列问题:
(1)求上表中的数据,的值;
(2)通过计算,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)如果比赛成绩在80分以上(含80分)的选手为获奖选手,那么我们随机的从本次参赛的所有选手中抽取出一个人,求恰好抽中获奖选手的概率?
21.(本题满分12分)
已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求的值;
(2)求证:.
22.(本题满分12分)
为实现区域教育均衡发展,我市计划对某县、两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所类学校和两所类学校共需资金230万元;改造两所类学校和一所类学校共需资金205万元.
(1)改造一所类学校和一所类学校所需的资金分别是多少万元?
(2)若该县的类学校不超过5所,则类学校至少有多少所?
(3)我市计划今年对该县、两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到、两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
23.(本题满分12分)
如图,内接于半圆,是直径,过作直线使.是弧的中点,交于,于,交于.
(1)求证:是半圆的切线;
(2)求证:.
(3)若的面积为4.5,且,,求的面积.
24.(本题满分12分)
如图,抛物线与轴交于点,与轴交于、两点,点在点左侧.点的坐标为,.
(1)求抛物线的解析式;
(2)若点是线段下方抛物线上的动点,求四边形面积的最大值;
(3)若点在轴上,点在抛物线上.是否存在以、、、为顶点且以为一边的平行四边形 若存在,求点的坐标;若不存在,请说明理由.
25.(本题满分14分)
如图1,已知直线与轴、轴分别交于点和点,过直线上的两点、分别作轴的垂线段,垂足分别为和,其中,.
(1)如果,,试判断的形状;
(2)如果,(1)中有关的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;
(3)如图2,题目中的条件不变,如果,并且,求经过、、三点的抛物线所对应的函数关系式;
(4)在(3)的条件下,如果抛物线的对称轴与线段交于点,点是对称轴上一动点,以点、、为顶点的三角形和以点、、为顶点的三角形相似,求符合条件的点的坐标.
绵阳市重点中学2023-2024学年高一上学期新生入学考试
数学试卷
参考答案及评分标准
一、选择题(每个小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A C B A B D A D C B D C
二、填空题(每个小题4分,共24分)
13. 14.216° 15.-1 16.18 17.5或2 18.2022.5
三、解答:(共90分)
19.解(1)原式
(2)原式
把代入得原式.
20.解(1)∵总人数(人)
∴,.
(2)由(1)的计算知70至80分段的人数为90人,
90至100分段的人数人,
补全条形图如下图所示:
(3)比赛成绩的中位数落在:70~80分.
(4)恰好抽中获奖选手的概率为:.
21.解(1)由,解得,所以
,.
在中,,,
∴.
(2)取点关于原点的对称点,则问题转化为求证.
由勾股定理可得,,,,
∵,
∴是等腰直角三角形.∴.∴.
22.解(1)设改造一所类学校和一所类学校所需的改造资金分别为万元和万元.
依题意得:
解之得
答:改造一所类学校和一所类学校所需的改造资金分别为60万元和85万元.
(2)设该县有、两类学校分别为所和所.
则
∵类学校不超过5所∴∴.
即:类学校至少有15所.
(3)设今年改造类学校所,则改造类学校为所,
依题意得:
解之得.
∵取整数∴
即:共有4种方案.
23.证明(1):∵是直径∴,
∵∴,即
∴是半圆的切线.
(2)如图
∵是弧的中点,∴
∵是直径∴,故
∵,∴,
∴,∴.
(3)连结则,
∵,是弧的中点∴
∴,∴.
又∵,
∴
∴
∴.
(其它解法,请酌情评分)
24.解(1)∵点,,
把、代入得:
解得:,
∴所求抛物线的解析式为.
(2)过点作轴分别交线段和轴于点、.
∵对称轴,,∴点
∴
易得直线的解析式为
令,,其中,
当时,有最大值3
此时四边形面积有最大值.
(3)如图,有如下情况:
①过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形,
∵,
令得:,
∴点,
②平移直线交轴于点,交轴上方的抛物线于点,当时,四边形为平行四边形,
∵,∴由对称关系令,由
化简得:,解得或,
此时存在点和
综上,存在3个点符合题意,坐标分别是,,.
25.(1)是直角三角形.
依题意得,,,∴
在中,
在中,
∴
∴是直角三角形(解法不惟一).
(2)答:(1)中的结论还成立.
依题意得,,
∴
∴
∵∴
又∵在中,
在中,
∴
∴
∴是直角三角形.(解法不惟一).
(3)∵,,∴.
方法一:设抛物线的函数关系式为.
∵抛物线经过点、和
∴,∴
∴所求抛物线的函数关系式为.
方法二:设抛物线的函数关系式为.
∵抛物线经过点∴解得
∴所求抛物线的函数关系式为
即.
(4)抛物线的对称轴与轴的交点符合条件,
∵,,∴
∵抛物线的对称轴为,∴
∴.
过点作,交抛物线的对称轴于点.
∴、、和两两相似
∴即.
∵点位于第四象限,∴.
因此,符合条件的点有两个,分别是,.
(解法不惟一)
同课章节目录
