三角形的外角和(四川省巴中地区平昌县)
文档属性
| 名称 | 三角形的外角和(四川省巴中地区平昌县) |  | |
| 格式 | rar | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-03 17:44:00 | ||
图片预览


文档简介
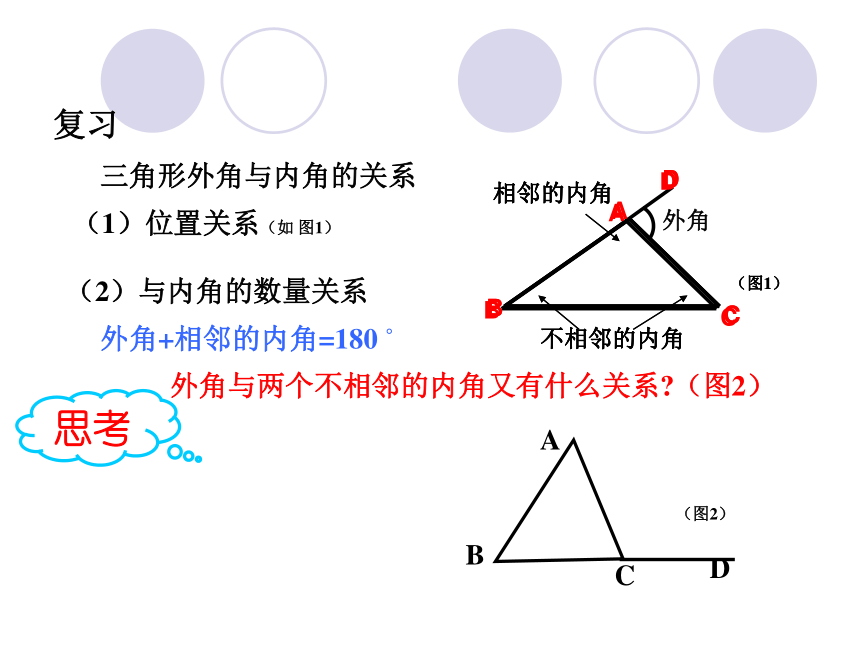
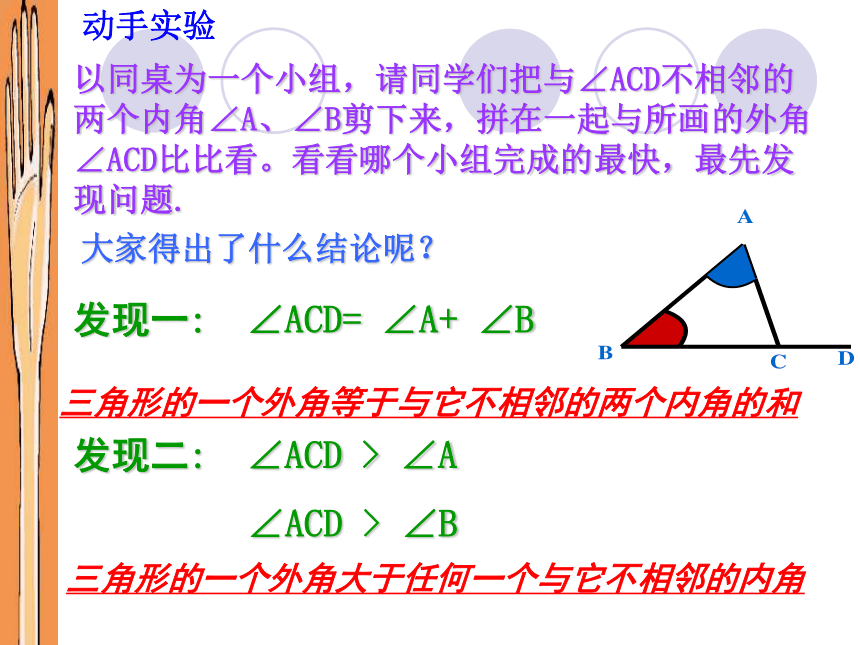
课件23张PPT。三角形的外角和坦溪小学张松柏 2007�427外角相邻的内角不相邻的内角复习三角形外角与内角的关系(1)位置关系(如 图1)(2)与内角的数量关系外角+相邻的内角=180 ?外角与两个不相邻的内角又有什么关系?(图2)(图1)(图2)思考相邻的内角不相邻的内角(图1)ABCDBCDABCD以同桌为一个小组,请同学们把与∠ACD不相邻的两个内角∠A、∠B剪下来,拼在一起与所画的外角∠ACD比比看。看看哪个小组完成的最快,最先发现问题.大家得出了什么结论呢?发现一: ∠ACD= ∠A+ ∠B发现二: ∠ACD > ∠A
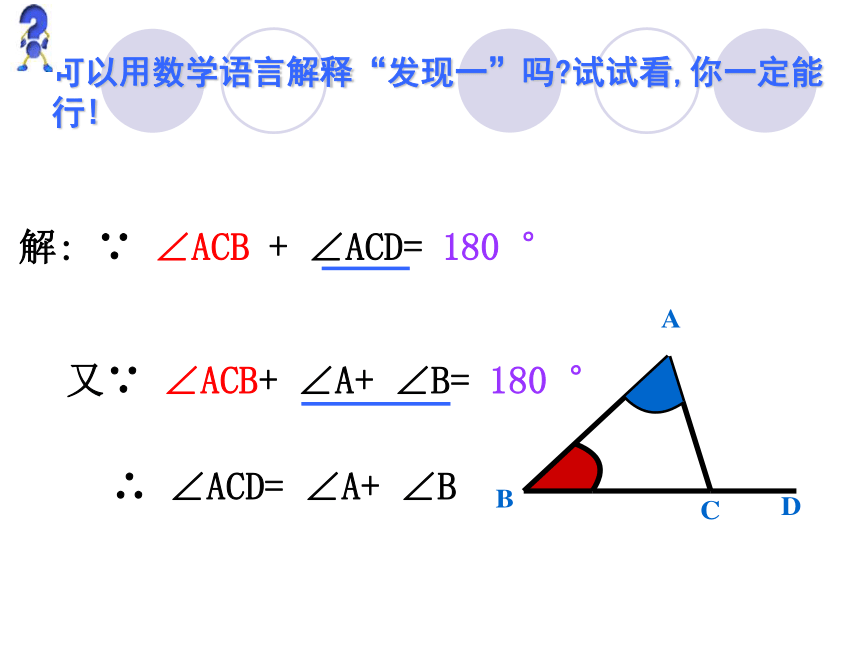
∠ACD > ∠B动手实验三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角大于任何一个与它不相邻的内角可以用数学语言解释“发现一”吗?试试看,你一定能行!解: ∵ ∠ACB + ∠ACD= 180 °又∵ ∠ACB+ ∠A+ ∠B= 180 ° ∴ ∠ACD= ∠A+ ∠B三角形外角与内角之间的关系
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
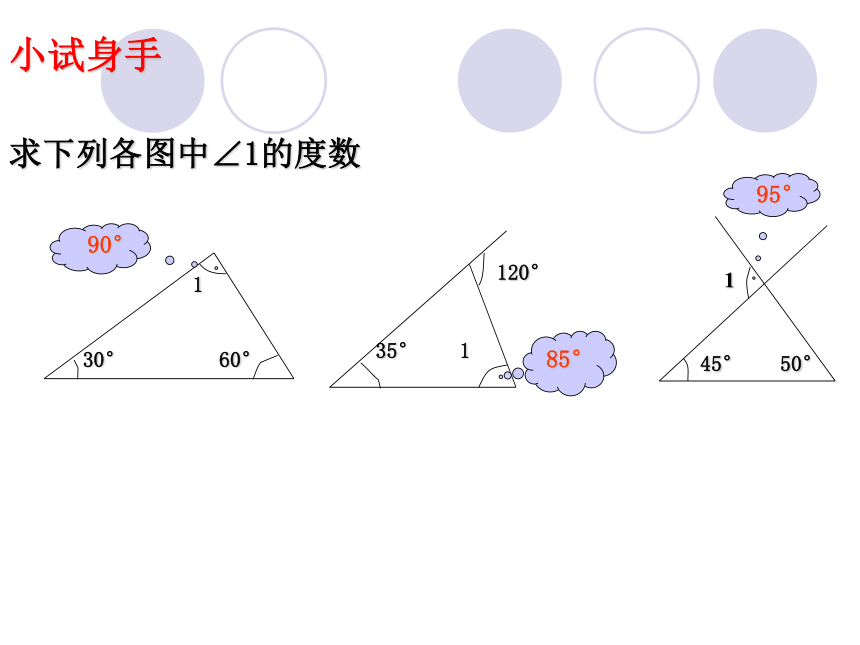
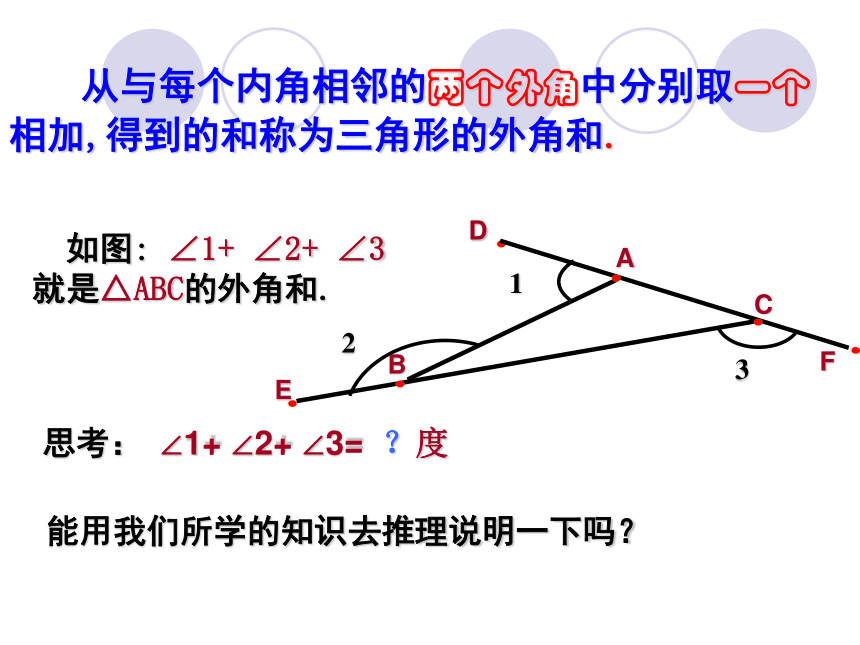
不相邻的内角。等于大于互补小试身手求下列各图中∠1的度数 三角形内角和是180 °三角形的外角和是多少呢?1.什么是三角形的外角和?2.三角形有固定外角和吗?3.如果有,三角形的外角和是多少呢? 从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图: ∠1+ ∠2+ ∠3就是△ABC的外角和.
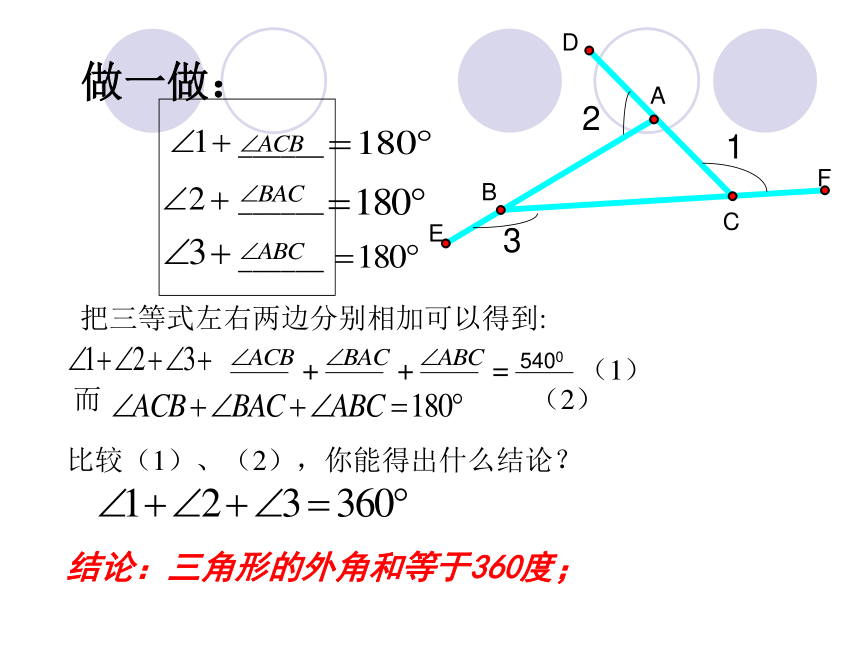
思考: ∠1+ ∠2+ ∠3= ?度能用我们所学的知识去推理说明一下吗?做一做:比较(1)、(2),你能得出什么结论?结论:三角形的外角和等于360度;5400三角形的外角和等于3600让 我 们 展 开 想 象 的 翅 膀例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解 :(1)∵ ∠ADC是⊿ABD的外角 (已知)∴∠ADC=∠B+∠BAD=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD∴∠B=40 ? (2)∵在⊿ABC中 ∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?∠3 > ∠1∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠12、如图:∠1=25°,
∠2=95°,∠3=30°,
则∠4=_______30°练一练F∠A+∠B+∠C+∠D+∠E+∠F= .DEF360°NPMF3、动脑筋,想一想1 三角形的外角性质: 三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的内角和等于180?三角形的外角和等于360 ?3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。我们的收获再 见知识拓展知识拓展可要动脑哟CBOACBOA方法二:解:过C点作 CE∥AB∵ CE∥AB∴ ∠ACE = ∠A ( ? )
∠DCE = ∠B ( ? )∴ ∠ACD = ∠ACE+ ∠DCE
= ∠A+ ∠B课后动脑筋:还有其它作辅助线的方法吗 ?E外角3、三角形外角与内角的关系(1)位置关系(2)数量关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角1、什么是三角形的内角?其和等于多少?复习2、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?例 2 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC
∠ACD > ∠B动手实验三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角大于任何一个与它不相邻的内角可以用数学语言解释“发现一”吗?试试看,你一定能行!解: ∵ ∠ACB + ∠ACD= 180 °又∵ ∠ACB+ ∠A+ ∠B= 180 ° ∴ ∠ACD= ∠A+ ∠B三角形外角与内角之间的关系
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
不相邻的内角。等于大于互补小试身手求下列各图中∠1的度数 三角形内角和是180 °三角形的外角和是多少呢?1.什么是三角形的外角和?2.三角形有固定外角和吗?3.如果有,三角形的外角和是多少呢? 从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图: ∠1+ ∠2+ ∠3就是△ABC的外角和.
思考: ∠1+ ∠2+ ∠3= ?度能用我们所学的知识去推理说明一下吗?做一做:比较(1)、(2),你能得出什么结论?结论:三角形的外角和等于360度;5400三角形的外角和等于3600让 我 们 展 开 想 象 的 翅 膀例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解 :(1)∵ ∠ADC是⊿ABD的外角 (已知)∴∠ADC=∠B+∠BAD=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD∴∠B=40 ? (2)∵在⊿ABC中 ∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?∠3 > ∠1∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠12、如图:∠1=25°,
∠2=95°,∠3=30°,
则∠4=_______30°练一练F∠A+∠B+∠C+∠D+∠E+∠F= .DEF360°NPMF3、动脑筋,想一想1 三角形的外角性质: 三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的内角和等于180?三角形的外角和等于360 ?3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。我们的收获再 见知识拓展知识拓展可要动脑哟CBOACBOA方法二:解:过C点作 CE∥AB∵ CE∥AB∴ ∠ACE = ∠A ( ? )
∠DCE = ∠B ( ? )∴ ∠ACD = ∠ACE+ ∠DCE
= ∠A+ ∠B课后动脑筋:还有其它作辅助线的方法吗 ?E外角3、三角形外角与内角的关系(1)位置关系(2)数量关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角1、什么是三角形的内角?其和等于多少?复习2、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?例 2 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC
