数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 951.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 22:16:07 | ||
图片预览





文档简介
(共15张PPT)
1.4.1用空间向量研究
直线、平面的位置关系
求法向量的方法
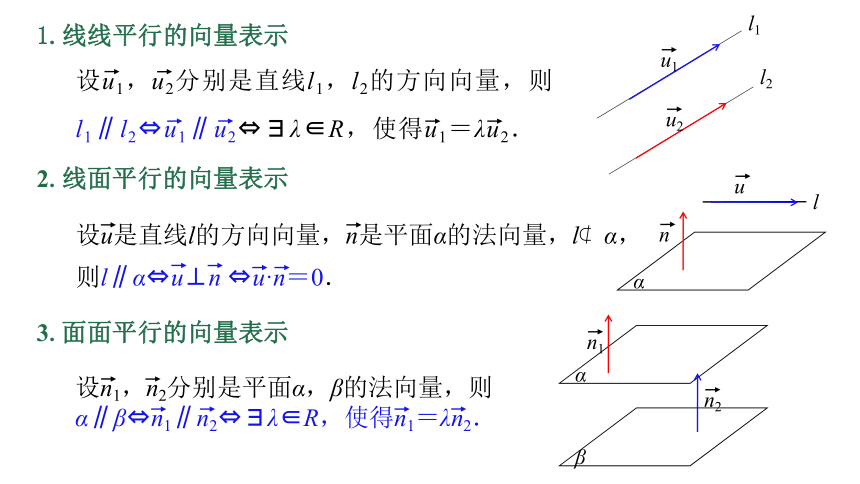
1.线线平行的向量表示
设u1,u2分别是直线l1,l2的方向向量,则
l1∥l2 u1∥u2 λ∈R,使得u1=λu2.
l1
l2
u1
u2
设u是直线l的方向向量,n是平面α的法向量,l α,
则l∥α u⊥n u·n=0.
α
u
n
l
2.线面平行的向量表示
3.面面平行的向量表示
设n1,n2分别是平面α,β的法向量,则
α∥β n1∥n2 λ∈R,使得n1=λn2.
α
β
n1
n2
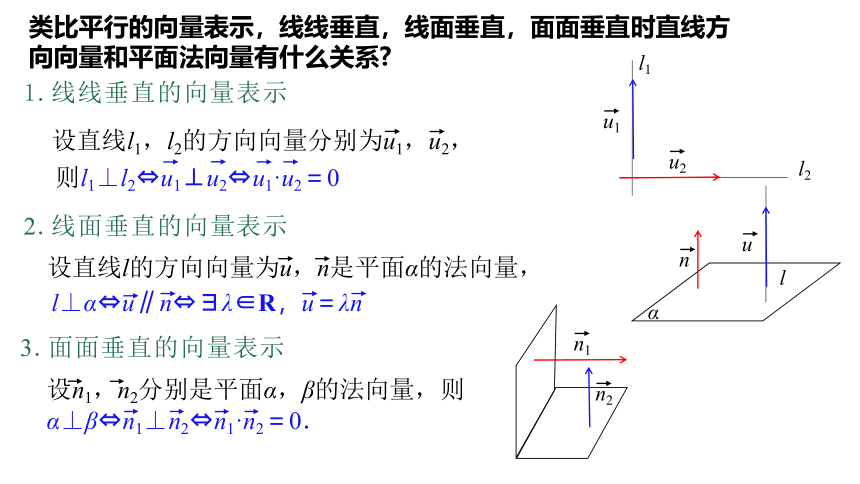
类比平行的向量表示,线线垂直,线面垂直,面面垂直时直线方向向量和平面法向量有什么关系
1.线线垂直的向量表示
设直线l1,l2的方向向量分别为u1,u2,
则l1⊥l2 u1⊥u2 u1·u2=0
l1
u1
l2
u2
2.线面垂直的向量表示
设直线l的方向向量为u,n是平面α的法向量,
l⊥α u∥n λ∈R,u=λn
α
n
l
u
3.面面垂直的向量表示
设n1,n2分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
n1
n2
例1.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.
B
A
C
D
P
E
F
方法1:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
x
y
z
设AD=a,则A(0,0,0),P(0,0,1),B(0,1,0),C(a,1,0),
∵E在BC上,∴设E(m,1,0),
∴无论点E在边BC上何处,总有PE⊥AF.
一、证明线线垂直问题
B
A
C
D
P
E
F
故无论点E在边BC上的何处,都有PE⊥AF.
变式:如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.求证:EF⊥BC.
A
B
C
D
E
F
由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴,在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系,
x
y
z
例2:如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
y
z
O1
即AB1⊥BA1,AB1⊥BD.又因为BA1∩BD=B,所以AB1⊥平面A1BD.
二、证明线面垂直问题
A
B
C
A1
B1
C1
D
O
x
O1
y
z
方法二:设平面A1BD的法向量为n=(x,y,z),
三、证明面面垂直问题
1.4.1用空间向量研究
直线、平面的位置关系
求法向量的方法
1.线线平行的向量表示
设u1,u2分别是直线l1,l2的方向向量,则
l1∥l2 u1∥u2 λ∈R,使得u1=λu2.
l1
l2
u1
u2
设u是直线l的方向向量,n是平面α的法向量,l α,
则l∥α u⊥n u·n=0.
α
u
n
l
2.线面平行的向量表示
3.面面平行的向量表示
设n1,n2分别是平面α,β的法向量,则
α∥β n1∥n2 λ∈R,使得n1=λn2.
α
β
n1
n2
类比平行的向量表示,线线垂直,线面垂直,面面垂直时直线方向向量和平面法向量有什么关系
1.线线垂直的向量表示
设直线l1,l2的方向向量分别为u1,u2,
则l1⊥l2 u1⊥u2 u1·u2=0
l1
u1
l2
u2
2.线面垂直的向量表示
设直线l的方向向量为u,n是平面α的法向量,
l⊥α u∥n λ∈R,u=λn
α
n
l
u
3.面面垂直的向量表示
设n1,n2分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
n1
n2
例1.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.
B
A
C
D
P
E
F
方法1:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
x
y
z
设AD=a,则A(0,0,0),P(0,0,1),B(0,1,0),C(a,1,0),
∵E在BC上,∴设E(m,1,0),
∴无论点E在边BC上何处,总有PE⊥AF.
一、证明线线垂直问题
B
A
C
D
P
E
F
故无论点E在边BC上的何处,都有PE⊥AF.
变式:如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.求证:EF⊥BC.
A
B
C
D
E
F
由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴,在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系,
x
y
z
例2:如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
y
z
O1
即AB1⊥BA1,AB1⊥BD.又因为BA1∩BD=B,所以AB1⊥平面A1BD.
二、证明线面垂直问题
A
B
C
A1
B1
C1
D
O
x
O1
y
z
方法二:设平面A1BD的法向量为n=(x,y,z),
三、证明面面垂直问题
