人教版 八年级数学上册试题 11.1与三角形有关的线段-(含答案)
文档属性
| 名称 | 人教版 八年级数学上册试题 11.1与三角形有关的线段-(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览


文档简介
11.1与三角形有关的线段
一.选择题
1.已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )
A.2cm B.3cm C.6cm D.13cm
2.电动伸缩门是依据平行四边形的( )
A.对边平行 B.伸缩性 C.容易变形 D.稳定性
3.已知三角形的三边长分别为3,4,x,且x为整数,则x的最大值为( )
A.8 B.7 C.5 D.6
4.如图,AC⊥BC,DE⊥BC,下列说法正确的是( )
A.DE是△ABE的高 B.AC是△ABE的高
C.BE是△ABE的高 D.BC是△ABE的高
5.下列说法中,不正确的是( )
A.对顶角相等
B.三角形具有稳定性
C.平行于同一直线的两直线互相平行
D.内错角相等
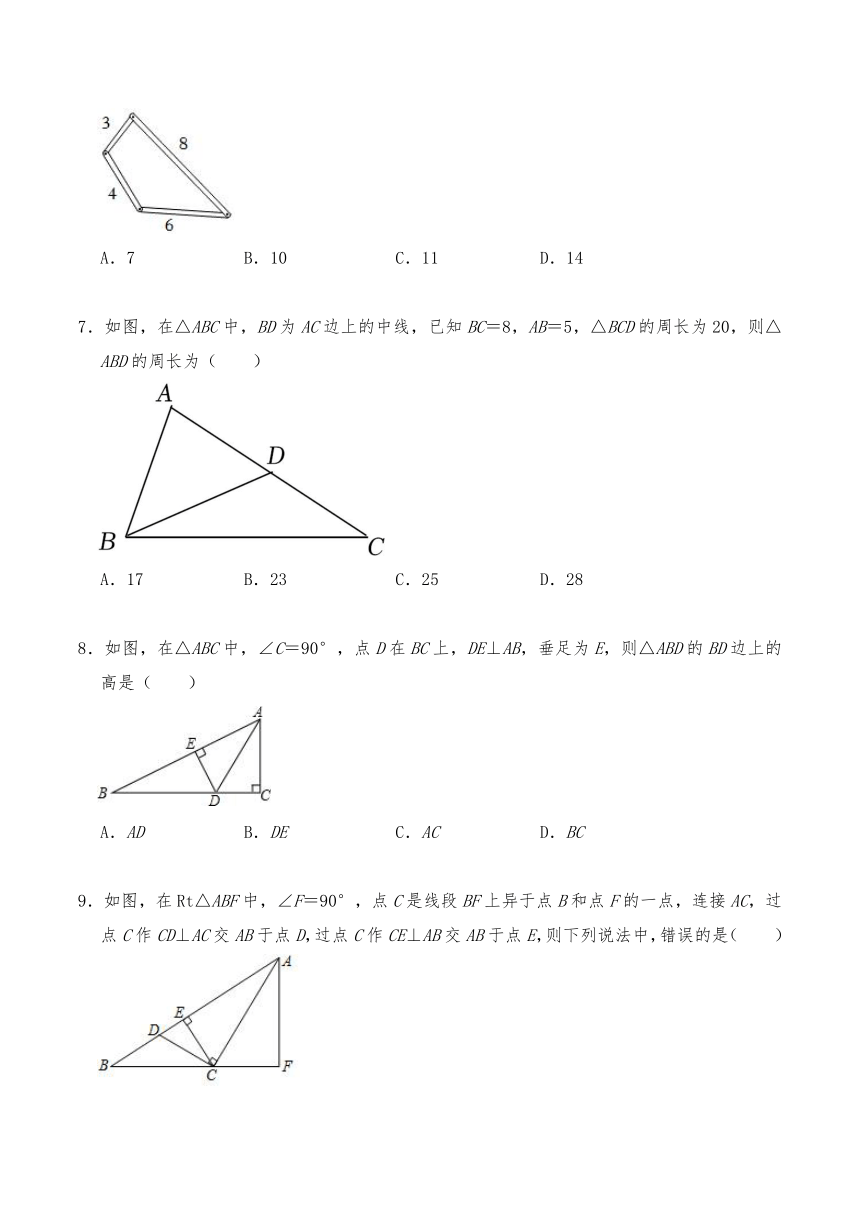
6.如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为3、4、6、8,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
A.7 B.10 C.11 D.14
7.如图,在△ABC中,BD为AC边上的中线,已知BC=8,AB=5,△BCD的周长为20,则△ABD的周长为( )
A.17 B.23 C.25 D.28
8.如图,在△ABC中,∠C=90°,点D在BC上,DE⊥AB,垂足为E,则△ABD的BD边上的高是( )
A.AD B.DE C.AC D.BC
9.如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )
A.△ABC中,AB边上的高是CE
B.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CE
D.△ACD中,CD边上的高是AC
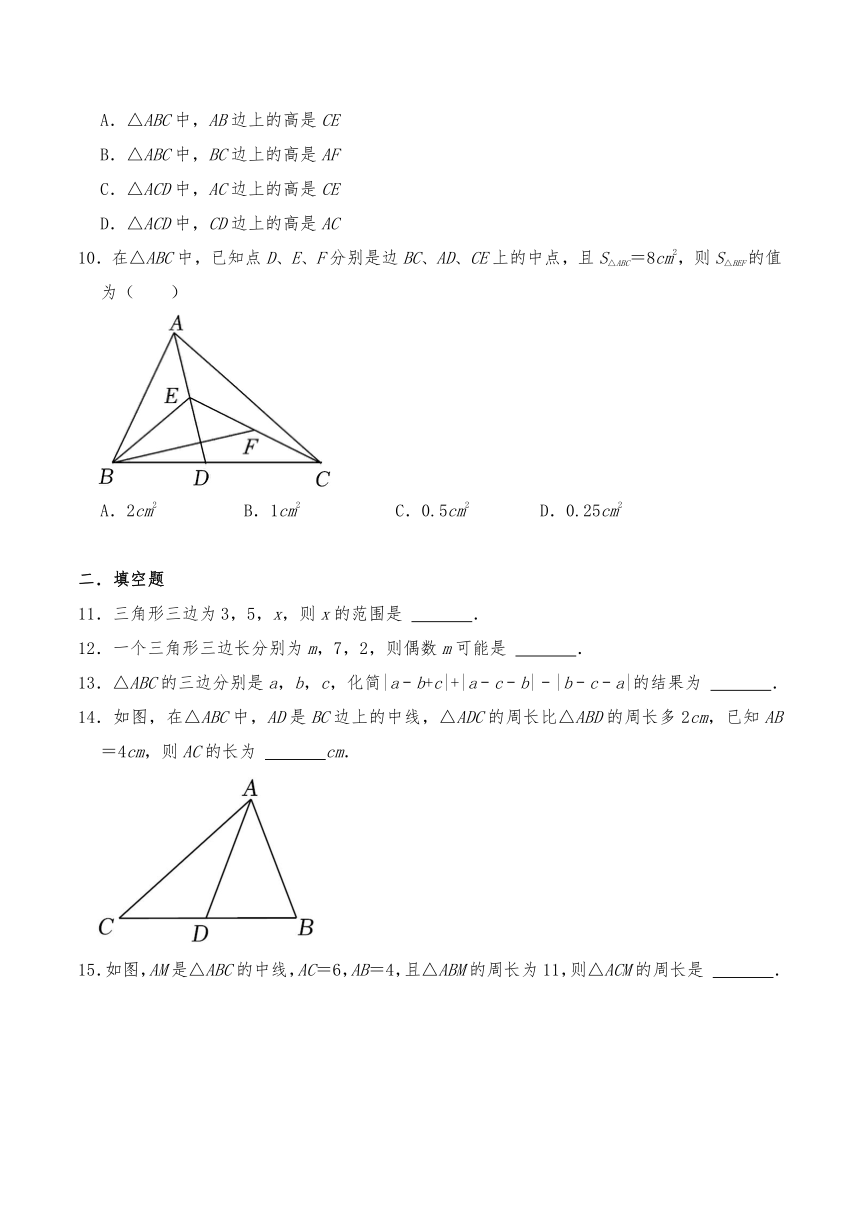
10.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=8cm2,则S△BEF的值为( )
A.2cm2 B.1cm2 C.0.5cm2 D.0.25cm2
二.填空题
11.三角形三边为3,5,x,则x的范围是 .
12.一个三角形三边长分别为m,7,2,则偶数m可能是 .
13.△ABC的三边分别是a,b,c,化简|a﹣b+c|+|a﹣c﹣b|﹣|b﹣c﹣a|的结果为 .
14.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多2cm,已知AB=4cm,则AC的长为 cm.
15.如图,AM是△ABC的中线,AC=6,AB=4,且△ABM的周长为11,则△ACM的周长是 .
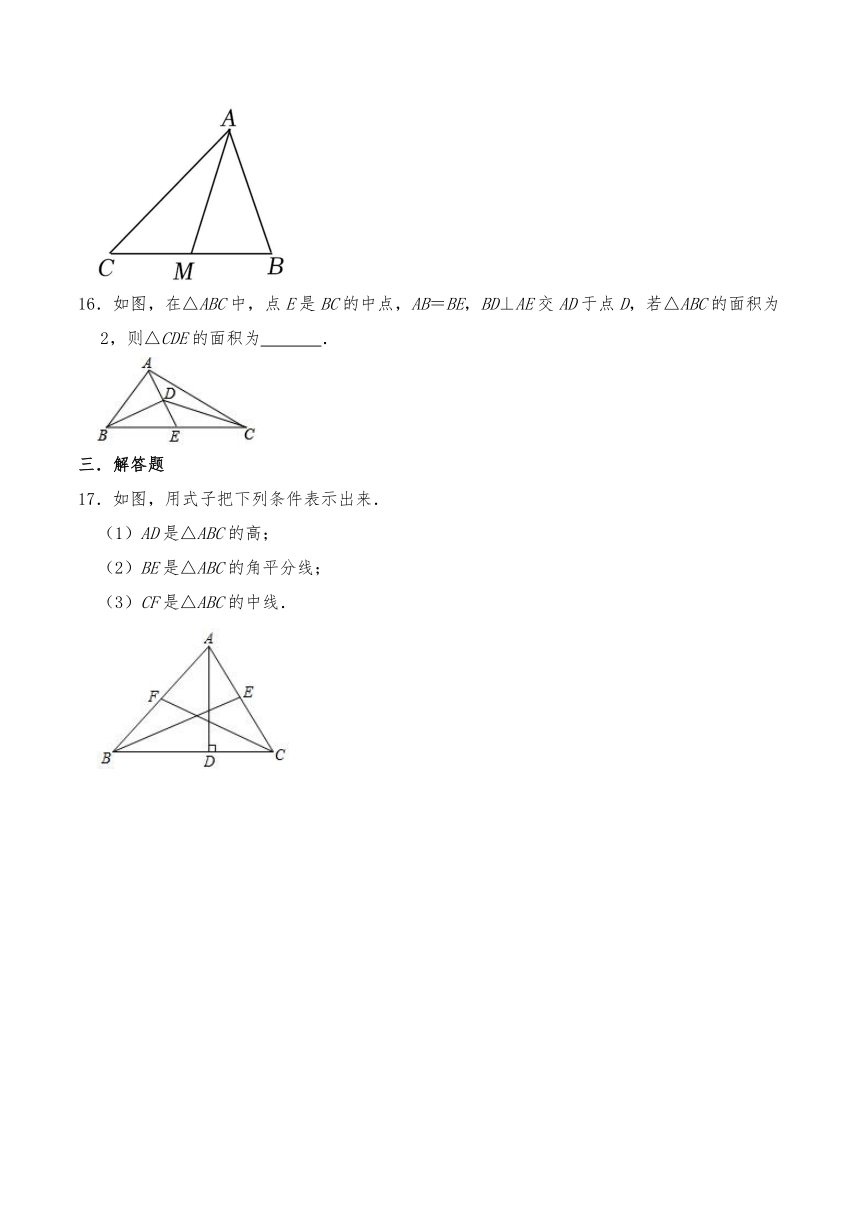
16.如图,在△ABC中,点E是BC的中点,AB=BE,BD⊥AE交AD于点D,若△ABC的面积为2,则△CDE的面积为 .
三.解答题
17.如图,用式子把下列条件表示出来.
(1)AD是△ABC的高;
(2)BE是△ABC的角平分线;
(3)CF是△ABC的中线.
18.已知a,b,c是一个三角形的三边长,
(1)填入“>、<或=”号:a﹣b﹣c 0,b﹣a﹣c 0,c+b﹣a 0.
(2)化简:|a﹣b﹣c|+|b﹣a﹣c|﹣|c+b﹣a|.
19.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
20.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
21.在△ABC中,BC=8,AB=1;
(1)若AC是整数,求AC的长;
(2)已知BD是△ABC的中线,若△ABD的周长为10,求△BCD的周长.
22.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
答案
一.选择题
C.C.D.B.D.B.A.C.C.A.
二.填空题
11.2<x<8.
12.6,8.
13.b+c﹣a.
14.6.
15.13.
16..
三.解答题
17.解:(1)由题意得:∠ADC=∠ADB=90°;
(2)由题意得:∠ABE=∠CBE;
(3)由题意得:AF=BF.
18.解:(1)∵a,b,c是一个三角形的三边长,
∴a﹣b﹣c<0,b﹣a﹣c<0,c+b﹣a>0,
故答案为:<,<,>;
(2)原式=b+c﹣a+a+c﹣b﹣c﹣b+a
=a﹣b+c.
19.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
20.解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9
21.解:(1)由题意得:BC﹣AB<AC<BC+AB,
∴7<AC<9,
∵AC是整数,
∴AC=8;
(2)∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为10,
∴AB+AD+BD=10,
∵AB=1,
∴AD+BD=9,
∴△BCD的周长=BC+BD+CD=BC+AD+CD=8+9=17.
22.解:(1)∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,
∴BC=8cm.
∵AD是BC边上的中线,
∴.
(2)不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15<AB=18,
∴不能构成三角形ABC,则不能求出DC的长.
一.选择题
1.已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )
A.2cm B.3cm C.6cm D.13cm
2.电动伸缩门是依据平行四边形的( )
A.对边平行 B.伸缩性 C.容易变形 D.稳定性
3.已知三角形的三边长分别为3,4,x,且x为整数,则x的最大值为( )
A.8 B.7 C.5 D.6
4.如图,AC⊥BC,DE⊥BC,下列说法正确的是( )
A.DE是△ABE的高 B.AC是△ABE的高
C.BE是△ABE的高 D.BC是△ABE的高
5.下列说法中,不正确的是( )
A.对顶角相等
B.三角形具有稳定性
C.平行于同一直线的两直线互相平行
D.内错角相等
6.如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为3、4、6、8,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
A.7 B.10 C.11 D.14
7.如图,在△ABC中,BD为AC边上的中线,已知BC=8,AB=5,△BCD的周长为20,则△ABD的周长为( )
A.17 B.23 C.25 D.28
8.如图,在△ABC中,∠C=90°,点D在BC上,DE⊥AB,垂足为E,则△ABD的BD边上的高是( )
A.AD B.DE C.AC D.BC
9.如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )
A.△ABC中,AB边上的高是CE
B.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CE
D.△ACD中,CD边上的高是AC
10.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=8cm2,则S△BEF的值为( )
A.2cm2 B.1cm2 C.0.5cm2 D.0.25cm2
二.填空题
11.三角形三边为3,5,x,则x的范围是 .
12.一个三角形三边长分别为m,7,2,则偶数m可能是 .
13.△ABC的三边分别是a,b,c,化简|a﹣b+c|+|a﹣c﹣b|﹣|b﹣c﹣a|的结果为 .
14.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多2cm,已知AB=4cm,则AC的长为 cm.
15.如图,AM是△ABC的中线,AC=6,AB=4,且△ABM的周长为11,则△ACM的周长是 .
16.如图,在△ABC中,点E是BC的中点,AB=BE,BD⊥AE交AD于点D,若△ABC的面积为2,则△CDE的面积为 .
三.解答题
17.如图,用式子把下列条件表示出来.
(1)AD是△ABC的高;
(2)BE是△ABC的角平分线;
(3)CF是△ABC的中线.
18.已知a,b,c是一个三角形的三边长,
(1)填入“>、<或=”号:a﹣b﹣c 0,b﹣a﹣c 0,c+b﹣a 0.
(2)化简:|a﹣b﹣c|+|b﹣a﹣c|﹣|c+b﹣a|.
19.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
20.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
21.在△ABC中,BC=8,AB=1;
(1)若AC是整数,求AC的长;
(2)已知BD是△ABC的中线,若△ABD的周长为10,求△BCD的周长.
22.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
答案
一.选择题
C.C.D.B.D.B.A.C.C.A.
二.填空题
11.2<x<8.
12.6,8.
13.b+c﹣a.
14.6.
15.13.
16..
三.解答题
17.解:(1)由题意得:∠ADC=∠ADB=90°;
(2)由题意得:∠ABE=∠CBE;
(3)由题意得:AF=BF.
18.解:(1)∵a,b,c是一个三角形的三边长,
∴a﹣b﹣c<0,b﹣a﹣c<0,c+b﹣a>0,
故答案为:<,<,>;
(2)原式=b+c﹣a+a+c﹣b﹣c﹣b+a
=a﹣b+c.
19.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
20.解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9
21.解:(1)由题意得:BC﹣AB<AC<BC+AB,
∴7<AC<9,
∵AC是整数,
∴AC=8;
(2)∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为10,
∴AB+AD+BD=10,
∵AB=1,
∴AD+BD=9,
∴△BCD的周长=BC+BD+CD=BC+AD+CD=8+9=17.
22.解:(1)∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,
∴BC=8cm.
∵AD是BC边上的中线,
∴.
(2)不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15<AB=18,
∴不能构成三角形ABC,则不能求出DC的长.
