人教版八年级数学上册试题 11.2.2三角形的外角(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 11.2.2三角形的外角(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 14:42:28 | ||
图片预览

文档简介
11.2.2三角形的外角
一.选择题
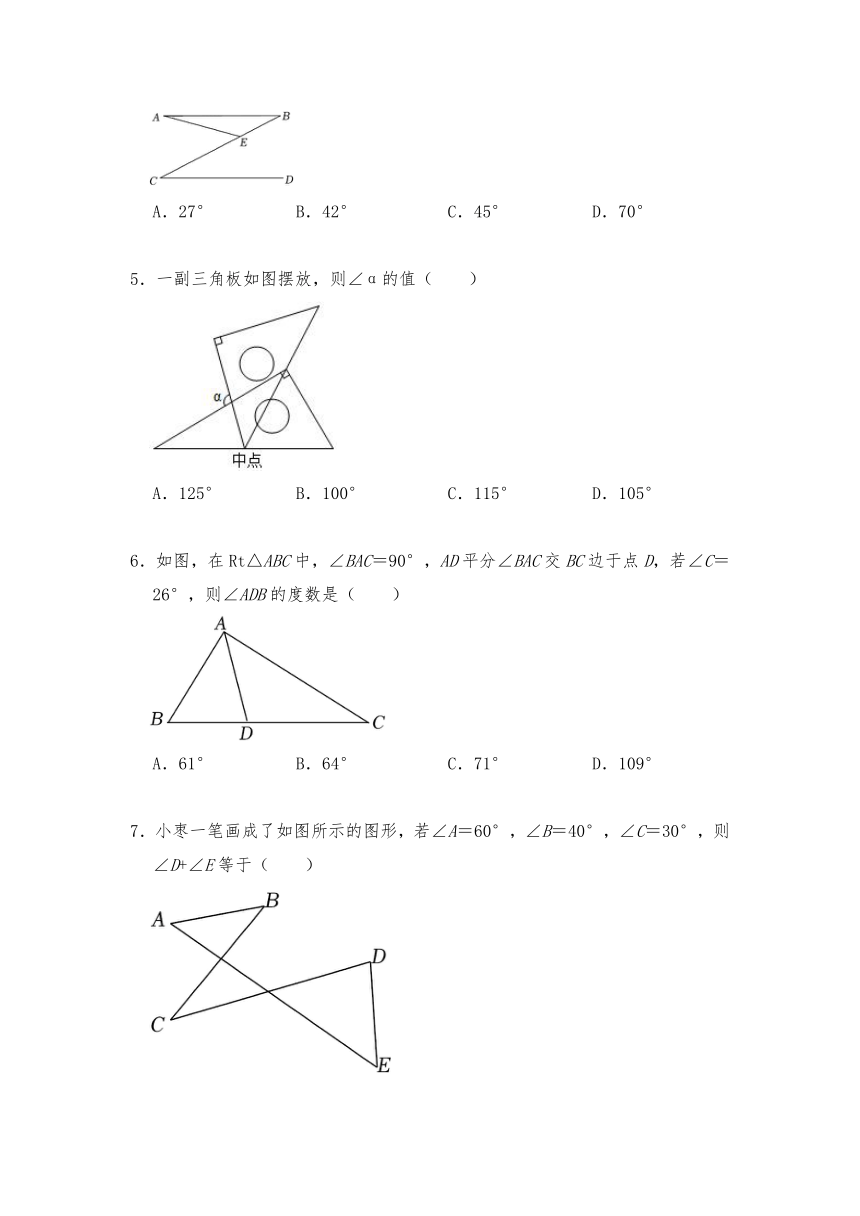
1.下列图形中,可以求出α度数的是( )
A. B.
C. D.
2.如图,直线a∥b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是( )
A.30° B.40° C.50° D.70°
3.如图,在△ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=55°,则∠EAC的度数是( )
A.55° B.60° C.65° D.70°
4.如图,直线AB∥CD,连接BC,点E是BC上一点,∠A=15°,∠C=27°,则∠AEC的大小为( )
A.27° B.42° C.45° D.70°
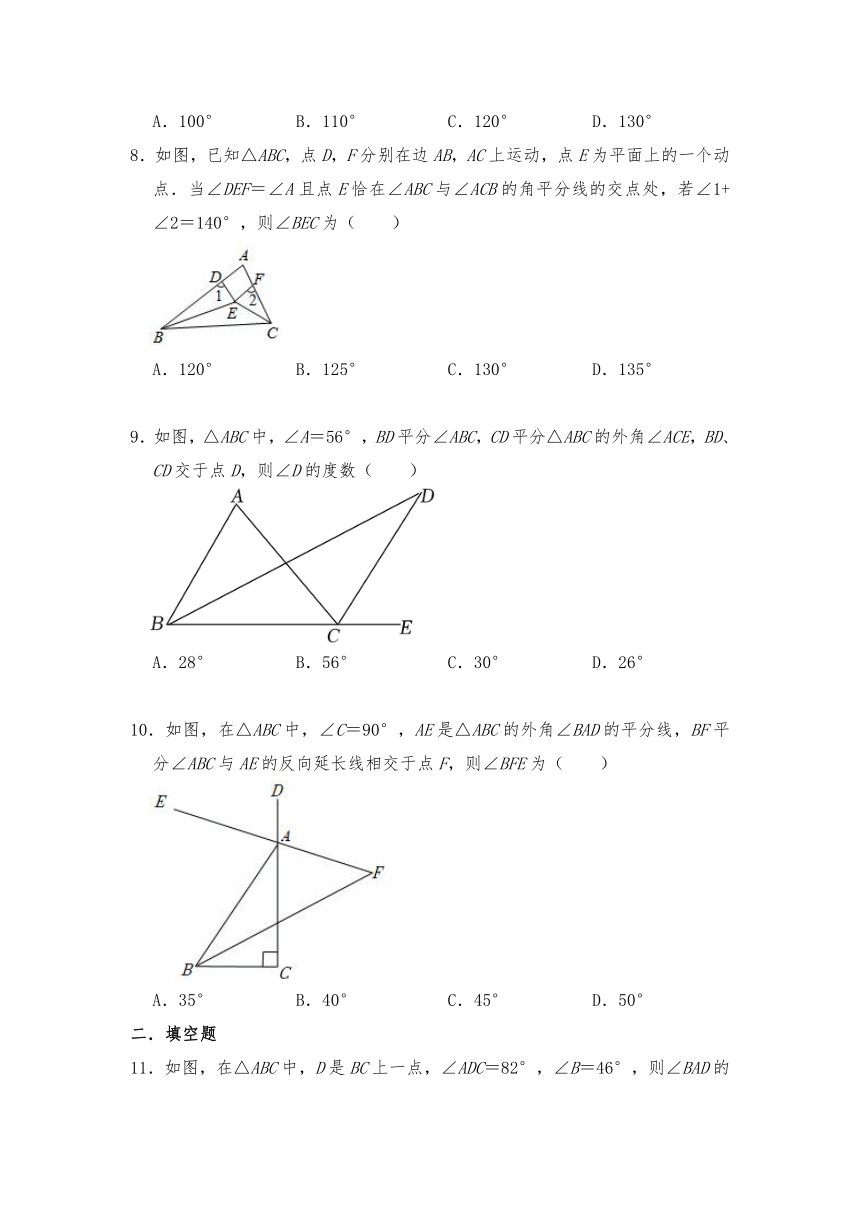
5.一副三角板如图摆放,则∠α的值( )
A.125° B.100° C.115° D.105°
6.如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC交BC边于点D,若∠C=26°,则∠ADB的度数是( )
A.61° B.64° C.71° D.109°
7.小枣一笔画成了如图所示的图形,若∠A=60°,∠B=40°,∠C=30°,则∠D+∠E等于( )
A.100° B.110° C.120° D.130°
8.如图,已知△ABC,点D,F分别在边AB,AC上运动,点E为平面上的一个动点.当∠DEF=∠A且点E恰在∠ABC与∠ACB的角平分线的交点处,若∠1+∠2=140°,则∠BEC为( )
A.120° B.125° C.130° D.135°
9.如图,△ABC中,∠A=56°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD交于点D,则∠D的度数( )
A.28° B.56° C.30° D.26°
10.如图,在△ABC中,∠C=90°,AE是△ABC的外角∠BAD的平分线,BF平分∠ABC与AE的反向延长线相交于点F,则∠BFE为( )
A.35° B.40° C.45° D.50°
二.填空题
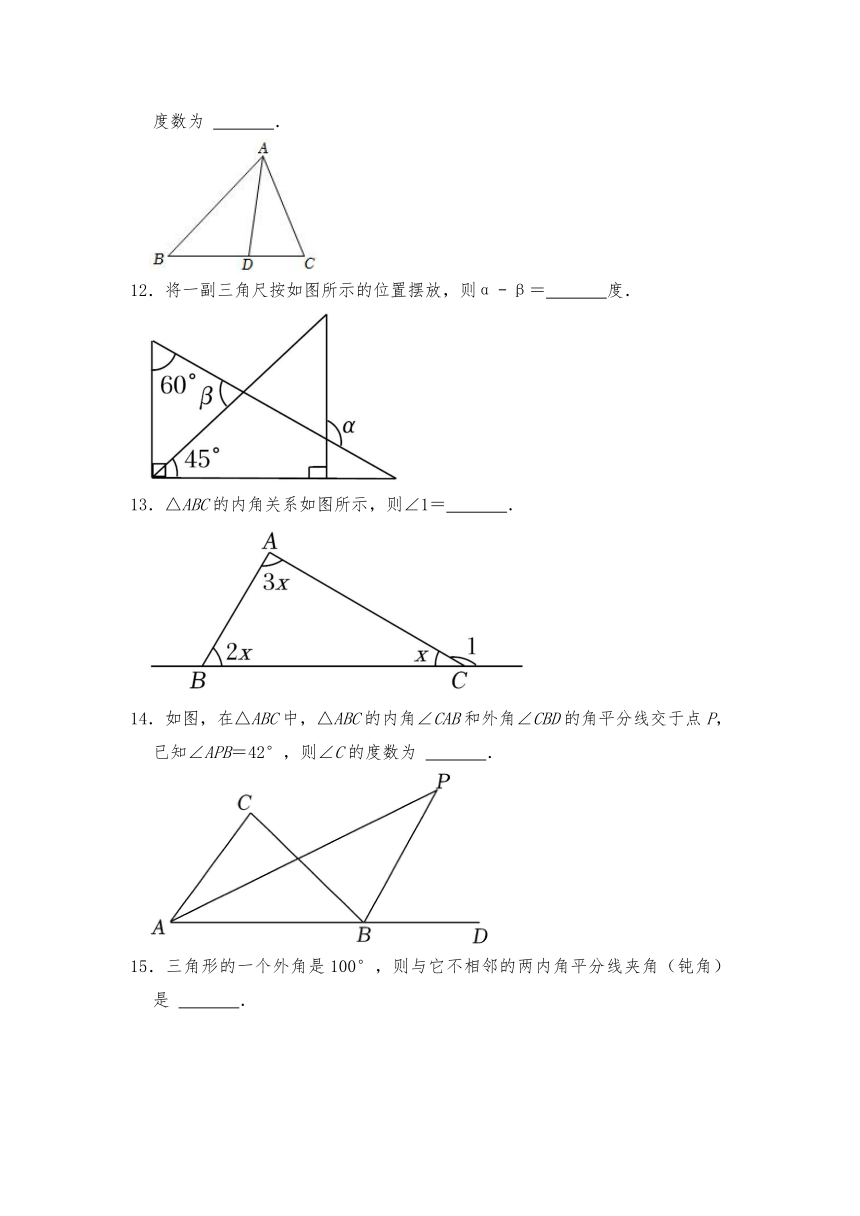
11.如图,在△ABC中,D是BC上一点,∠ADC=82°,∠B=46°,则∠BAD的度数为 .
12.将一副三角尺按如图所示的位置摆放,则α﹣β= 度.
13.△ABC的内角关系如图所示,则∠1= .
14.如图,在△ABC中,△ABC的内角∠CAB和外角∠CBD的角平分线交于点P,已知∠APB=42°,则∠C的度数为 .
15.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 .
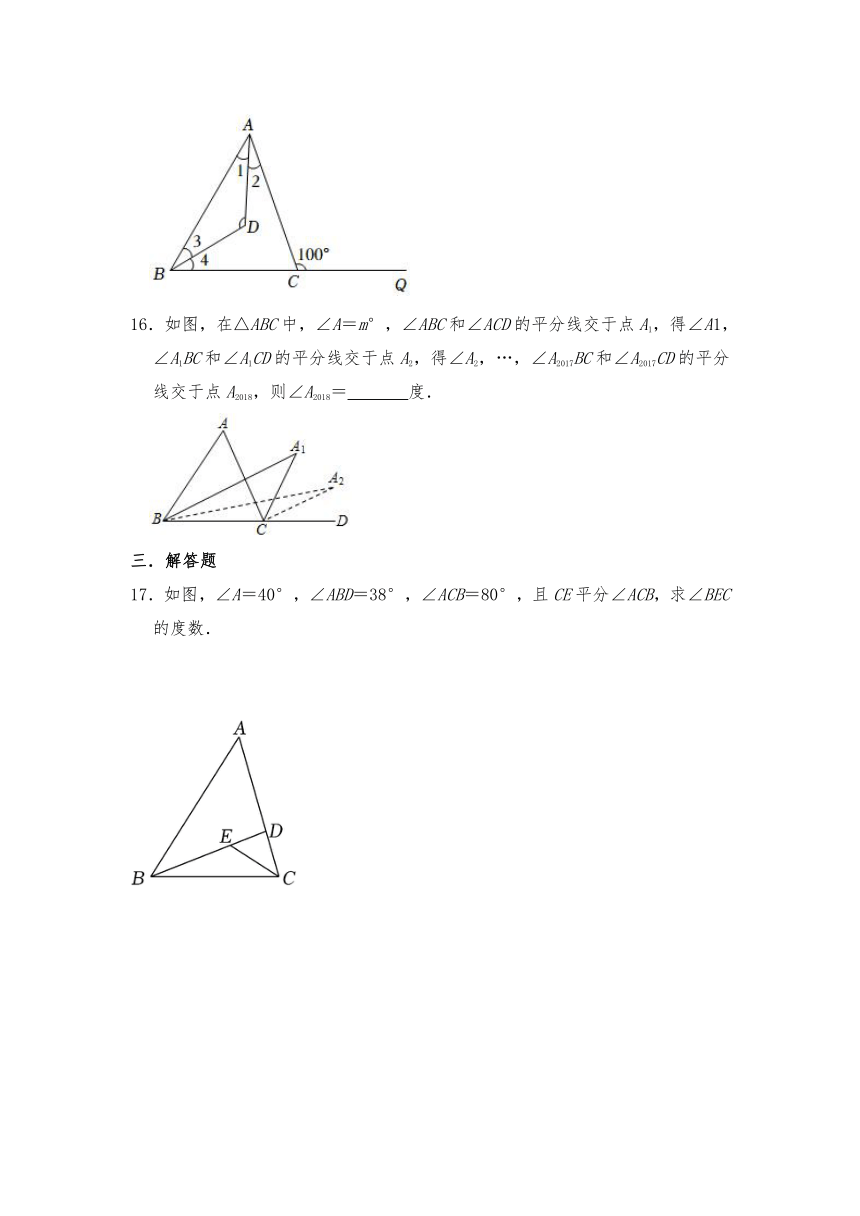
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,…,∠A2017BC和∠A2017CD的平分线交于点A2018,则∠A2018= 度.
三.解答题
17.如图,∠A=40°,∠ABD=38°,∠ACB=80°,且CE平分∠ACB,求∠BEC的度数.
18.如图,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数 .
19.(1)阅读并填空:如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.
解:因为BD平分∠ABC(已知),
所以∠1= ( ).
同理:∠2= .
所以∠1+∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°( ),
所以∠D= (等式性质).
即:∠D=90°+∠A.
(2)探究,请直接写出结果
(i)如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(3)拓展应用
请用以上结论解决下列问题:如图4,在△ABC中,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,
(i)∠A=80°,则∠F= ;
(ii)∠F=n°,则∠A= .
20.如图,点D为△ABC边BC的延长线上一点.
(1)若∠ABC﹣∠A=20°,∠ACD=140°,求∠A的度数;
(2)若∠ACD的角平分线与∠ABC的角平分线交于点M,过点C作CP⊥BM于点P.求证:∠MCP=90°﹣∠A.
21.如图,已知∠A=70°,∠B=50°,CE平分△ABC的外角∠ACD,求∠DCE的度数.
22.【探究】如图①,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)若∠ABC=80°,∠ACB=50°.则∠A= 度,∠P= 度.
(2)∠A与∠P的数量关系为 ,并说明理由.
【应用】如图②,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为 .
答案
一.选择题
B.B.C.B.D.C.B.B.A.C.
二.填空题
11.36°.
12.45.
13.150°.
14.84°.
15.130°.
16..
三.解答题
17.解:∵∠A=40°,∠ABD=38°,
∴∠BDC=∠A+∠ABD=40°+38°=78°,
∵CE平分∠ACB,
∴∠ACE=∠ACB=40°,
∴∠BEC=∠EDC+∠DCE=78°+40°=118°.
18.解:(1)由题意得:∠ACB=180°﹣(∠BAC+∠B)=180°﹣(70°+40°)=70°,
∵CE是∠ACB的平分线,
∴.
∵CD是高线,
∴∠ADC=90°,
∴∠ACD=90°﹣∠BAC=20°,
∴∠DCE=∠ACE﹣∠ACD=35°﹣20°=15°.
(2)由题意得:∠ACB=180°﹣(∠BAC+∠B)=180°﹣(α+β),
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=90°﹣(α+β).
∵CD是高线,
∴∠ADC=90°,
∴∠ACD=90°﹣∠BAC=90°﹣α,
∴∠DCE=∠ACE﹣∠ACD=90°﹣(α+β)﹣(90°﹣α)=.
故答案为:.
19.解:(1)解:因为BD平分∠ABC(已知),
所以∠1=∠ABC(角平分线定义).
同理:∠2=∠ACB.
所以∠1+∠2=(∠ABC+∠ACB),
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,(三角形的内角和等于180°),
所以∠D=180°﹣(∠ABC+∠ACB)(等式性质).
即:∠D=90°+∠A.
故答案为:ABC,ACB,(∠ABC+∠ACB),三角形的内角和等于180°,180°﹣(∠ABC+∠ACB).
(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A﹣2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
(ii)∠D与∠A之间的等量关系是:∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,
即:∠D=∠A,
故答案为:∠D=∠A;
(3)(i)由(1)知:∠D=90°+∠A.
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°﹣50°=310°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠CBE+∠BCN=(∠MBC+∠NCB)=155°,
∴∠E=180°﹣155°=25°,
由(2)(ii)知∠F=E=25°=12.5°,
故答案为:12.5°;
(ii)由(1)得∠D=90°+∠A,
∵BE、CE分别平分∠MBC、∠BCN,
∴2(∠EBC+∠ECB)+∠DBC+∠DCB=360°,
∵∠EBC+∠ECB=180°﹣∠E,∠DBC+∠DCB=180°﹣∠D,
∴2(180°﹣∠E)+180°﹣∠D=360°,
∴∠E=90°﹣∠D=90°﹣(90°+∠A)=45°﹣∠A,
∴∠F=90°﹣∠E=(45°﹣∠A)=n°,
∴∠A=180°﹣8n°.
故答案为:180°﹣8n°.
20.(1)解:∵∠ABC+∠A=∠ACD=140°,
又∵∠ABC﹣∠A=20°,
∴∠A=60°;
(2)证明:∵∠MCD是△MBC的外角,
∴∠M=∠MCD﹣∠MBC,
同理可证:∠A=∠ACD﹣∠ABC,
∵MC、MB分别平分∠ACD、∠ABC,
∴,
∴,
又∵CP⊥BM,
∴.
21.解:∵∠A=70°,∠B=50°,∠ACD为△ABC的外角,
∴∠ACD=∠A+∠B=120°,
∵CE平分∠ACD,
∴∠DCE=∠ACD=60°.
22.【解答】【探究】
解:(1)∵∠ABC=80°,∠ACB=50°,
∴∠A=1880°﹣80°﹣50°=50°,
∵∠ABC的平分线与∠ACB的平分线相交于点P,
∴∠CBP=∠ABC,∠BCP=∠ACB,
∴∠BCP+∠CBP=(∠ABC+∠ACB)=×130°=65°,
∴∠P=180°﹣65°=115°,
故答案为:50,115;
(2)∠P﹣∠A=90°.理由如下:
∵BP、CP分别平分∠ABC、∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°,
∴∠P+(∠ABC+∠ACB)=180°,
∴∠P+(180°﹣∠A)=180°,
∴∠P﹣∠A=90°;
故答案为:∠P﹣∠A=90°;
【应用】
解:∠Q=90°﹣∠A.理由如下:
∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q,
∴∠CBQ=(180°﹣∠ABC)=90°﹣∠ABC,
∠BCQ=(180°﹣∠ACB)=90°﹣∠ACB,
∴△BCQ中,∠Q=180°﹣(∠CBQ+∠BCQ)=180°﹣(90°﹣∠ABC+90°﹣∠ACB)=(∠ABC+∠ACB),
又∵∠ABC+∠ACB=180°﹣∠A,
∴∠Q=(180°﹣∠A)=90°﹣∠A;
故答案为:∠Q=90°﹣∠A.
一.选择题
1.下列图形中,可以求出α度数的是( )
A. B.
C. D.
2.如图,直线a∥b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是( )
A.30° B.40° C.50° D.70°
3.如图,在△ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=55°,则∠EAC的度数是( )
A.55° B.60° C.65° D.70°
4.如图,直线AB∥CD,连接BC,点E是BC上一点,∠A=15°,∠C=27°,则∠AEC的大小为( )
A.27° B.42° C.45° D.70°
5.一副三角板如图摆放,则∠α的值( )
A.125° B.100° C.115° D.105°
6.如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC交BC边于点D,若∠C=26°,则∠ADB的度数是( )
A.61° B.64° C.71° D.109°
7.小枣一笔画成了如图所示的图形,若∠A=60°,∠B=40°,∠C=30°,则∠D+∠E等于( )
A.100° B.110° C.120° D.130°
8.如图,已知△ABC,点D,F分别在边AB,AC上运动,点E为平面上的一个动点.当∠DEF=∠A且点E恰在∠ABC与∠ACB的角平分线的交点处,若∠1+∠2=140°,则∠BEC为( )
A.120° B.125° C.130° D.135°
9.如图,△ABC中,∠A=56°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD交于点D,则∠D的度数( )
A.28° B.56° C.30° D.26°
10.如图,在△ABC中,∠C=90°,AE是△ABC的外角∠BAD的平分线,BF平分∠ABC与AE的反向延长线相交于点F,则∠BFE为( )
A.35° B.40° C.45° D.50°
二.填空题
11.如图,在△ABC中,D是BC上一点,∠ADC=82°,∠B=46°,则∠BAD的度数为 .
12.将一副三角尺按如图所示的位置摆放,则α﹣β= 度.
13.△ABC的内角关系如图所示,则∠1= .
14.如图,在△ABC中,△ABC的内角∠CAB和外角∠CBD的角平分线交于点P,已知∠APB=42°,则∠C的度数为 .
15.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 .
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,…,∠A2017BC和∠A2017CD的平分线交于点A2018,则∠A2018= 度.
三.解答题
17.如图,∠A=40°,∠ABD=38°,∠ACB=80°,且CE平分∠ACB,求∠BEC的度数.
18.如图,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数 .
19.(1)阅读并填空:如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.试说明∠D=90°+∠A的理由.
解:因为BD平分∠ABC(已知),
所以∠1= ( ).
同理:∠2= .
所以∠1+∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°( ),
所以∠D= (等式性质).
即:∠D=90°+∠A.
(2)探究,请直接写出结果
(i)如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(3)拓展应用
请用以上结论解决下列问题:如图4,在△ABC中,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,
(i)∠A=80°,则∠F= ;
(ii)∠F=n°,则∠A= .
20.如图,点D为△ABC边BC的延长线上一点.
(1)若∠ABC﹣∠A=20°,∠ACD=140°,求∠A的度数;
(2)若∠ACD的角平分线与∠ABC的角平分线交于点M,过点C作CP⊥BM于点P.求证:∠MCP=90°﹣∠A.
21.如图,已知∠A=70°,∠B=50°,CE平分△ABC的外角∠ACD,求∠DCE的度数.
22.【探究】如图①,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)若∠ABC=80°,∠ACB=50°.则∠A= 度,∠P= 度.
(2)∠A与∠P的数量关系为 ,并说明理由.
【应用】如图②,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为 .
答案
一.选择题
B.B.C.B.D.C.B.B.A.C.
二.填空题
11.36°.
12.45.
13.150°.
14.84°.
15.130°.
16..
三.解答题
17.解:∵∠A=40°,∠ABD=38°,
∴∠BDC=∠A+∠ABD=40°+38°=78°,
∵CE平分∠ACB,
∴∠ACE=∠ACB=40°,
∴∠BEC=∠EDC+∠DCE=78°+40°=118°.
18.解:(1)由题意得:∠ACB=180°﹣(∠BAC+∠B)=180°﹣(70°+40°)=70°,
∵CE是∠ACB的平分线,
∴.
∵CD是高线,
∴∠ADC=90°,
∴∠ACD=90°﹣∠BAC=20°,
∴∠DCE=∠ACE﹣∠ACD=35°﹣20°=15°.
(2)由题意得:∠ACB=180°﹣(∠BAC+∠B)=180°﹣(α+β),
∵CE是∠ACB的平分线,
∴∠ACE=∠ACB=90°﹣(α+β).
∵CD是高线,
∴∠ADC=90°,
∴∠ACD=90°﹣∠BAC=90°﹣α,
∴∠DCE=∠ACE﹣∠ACD=90°﹣(α+β)﹣(90°﹣α)=.
故答案为:.
19.解:(1)解:因为BD平分∠ABC(已知),
所以∠1=∠ABC(角平分线定义).
同理:∠2=∠ACB.
所以∠1+∠2=(∠ABC+∠ACB),
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,(三角形的内角和等于180°),
所以∠D=180°﹣(∠ABC+∠ACB)(等式性质).
即:∠D=90°+∠A.
故答案为:ABC,ACB,(∠ABC+∠ACB),三角形的内角和等于180°,180°﹣(∠ABC+∠ACB).
(2)解:(i)∠D与∠A之间的等量关系是:∠D=90°﹣∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∴∠DBC+∠DCB+∠D=180°,
∴∠A+∠ABC+∠ACB=180°,
而∠ABC=180°﹣2∠DBC,
∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A﹣2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
(ii)∠D与∠A之间的等量关系是:∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D,
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,
即:∠D=∠A,
故答案为:∠D=∠A;
(3)(i)由(1)知:∠D=90°+∠A.
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°﹣50°=310°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠CBE+∠BCN=(∠MBC+∠NCB)=155°,
∴∠E=180°﹣155°=25°,
由(2)(ii)知∠F=E=25°=12.5°,
故答案为:12.5°;
(ii)由(1)得∠D=90°+∠A,
∵BE、CE分别平分∠MBC、∠BCN,
∴2(∠EBC+∠ECB)+∠DBC+∠DCB=360°,
∵∠EBC+∠ECB=180°﹣∠E,∠DBC+∠DCB=180°﹣∠D,
∴2(180°﹣∠E)+180°﹣∠D=360°,
∴∠E=90°﹣∠D=90°﹣(90°+∠A)=45°﹣∠A,
∴∠F=90°﹣∠E=(45°﹣∠A)=n°,
∴∠A=180°﹣8n°.
故答案为:180°﹣8n°.
20.(1)解:∵∠ABC+∠A=∠ACD=140°,
又∵∠ABC﹣∠A=20°,
∴∠A=60°;
(2)证明:∵∠MCD是△MBC的外角,
∴∠M=∠MCD﹣∠MBC,
同理可证:∠A=∠ACD﹣∠ABC,
∵MC、MB分别平分∠ACD、∠ABC,
∴,
∴,
又∵CP⊥BM,
∴.
21.解:∵∠A=70°,∠B=50°,∠ACD为△ABC的外角,
∴∠ACD=∠A+∠B=120°,
∵CE平分∠ACD,
∴∠DCE=∠ACD=60°.
22.【解答】【探究】
解:(1)∵∠ABC=80°,∠ACB=50°,
∴∠A=1880°﹣80°﹣50°=50°,
∵∠ABC的平分线与∠ACB的平分线相交于点P,
∴∠CBP=∠ABC,∠BCP=∠ACB,
∴∠BCP+∠CBP=(∠ABC+∠ACB)=×130°=65°,
∴∠P=180°﹣65°=115°,
故答案为:50,115;
(2)∠P﹣∠A=90°.理由如下:
∵BP、CP分别平分∠ABC、∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°,
∴∠P+(∠ABC+∠ACB)=180°,
∴∠P+(180°﹣∠A)=180°,
∴∠P﹣∠A=90°;
故答案为:∠P﹣∠A=90°;
【应用】
解:∠Q=90°﹣∠A.理由如下:
∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q,
∴∠CBQ=(180°﹣∠ABC)=90°﹣∠ABC,
∠BCQ=(180°﹣∠ACB)=90°﹣∠ACB,
∴△BCQ中,∠Q=180°﹣(∠CBQ+∠BCQ)=180°﹣(90°﹣∠ABC+90°﹣∠ACB)=(∠ABC+∠ACB),
又∵∠ABC+∠ACB=180°﹣∠A,
∴∠Q=(180°﹣∠A)=90°﹣∠A;
故答案为:∠Q=90°﹣∠A.
