人教版八年级数学上册试题 11.3多边形及其内角和(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 11.3多边形及其内角和(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 14:43:22 | ||
图片预览


文档简介
11.3多边形及其内角和
一.选择题
1.若正多边形的一个内角度数为144°,则这个多边形的边数为( )
A.10 B.12 C.8 D.7
2.一个正多边形的一个内角为90°,则这个正多边形的边数为( )
A.4 B.5 C.6 D.7
3.正八边形比正六边形的每个内角的度数多( )
A.15° B.30° C.45° D.60°
4.下列图中,内角和最小的是( )
A. B.
C. D.
5.一个多边形减去一个角后,所得多边形的内角和是720°,则这个多边形的边数不可能是( )
A.4 B.5 C.6 D.7
6.当多边形的边数增加1时,它的内角和与外角和( )
A.都不变
B.都增加180°
C.内角和增加180°,外角和减少180°
D.内角和增加180°,外角和不变
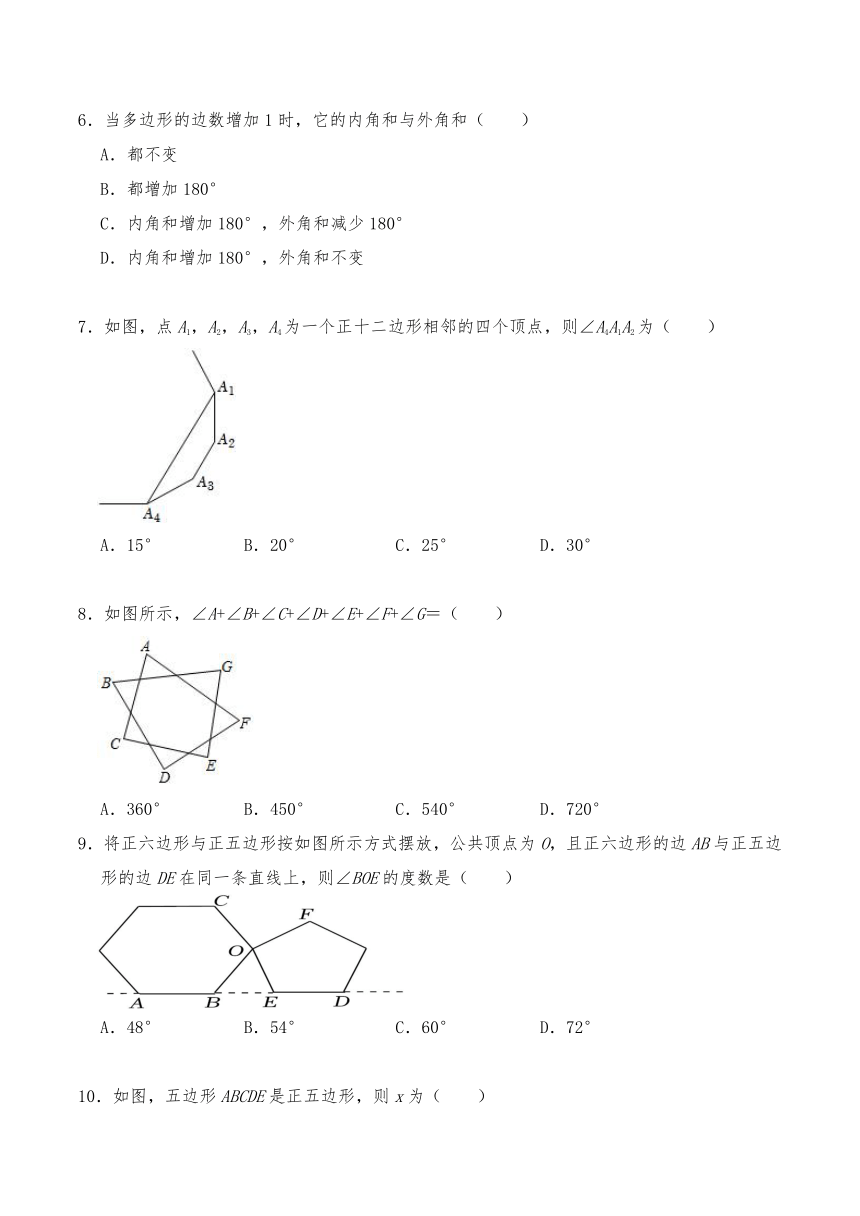
7.如图,点A1,A2,A3,A4为一个正十二边形相邻的四个顶点,则∠A4A1A2为( )
A.15° B.20° C.25° D.30°
8.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
A.360° B.450° C.540° D.720°
9.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
10.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
二.填空题
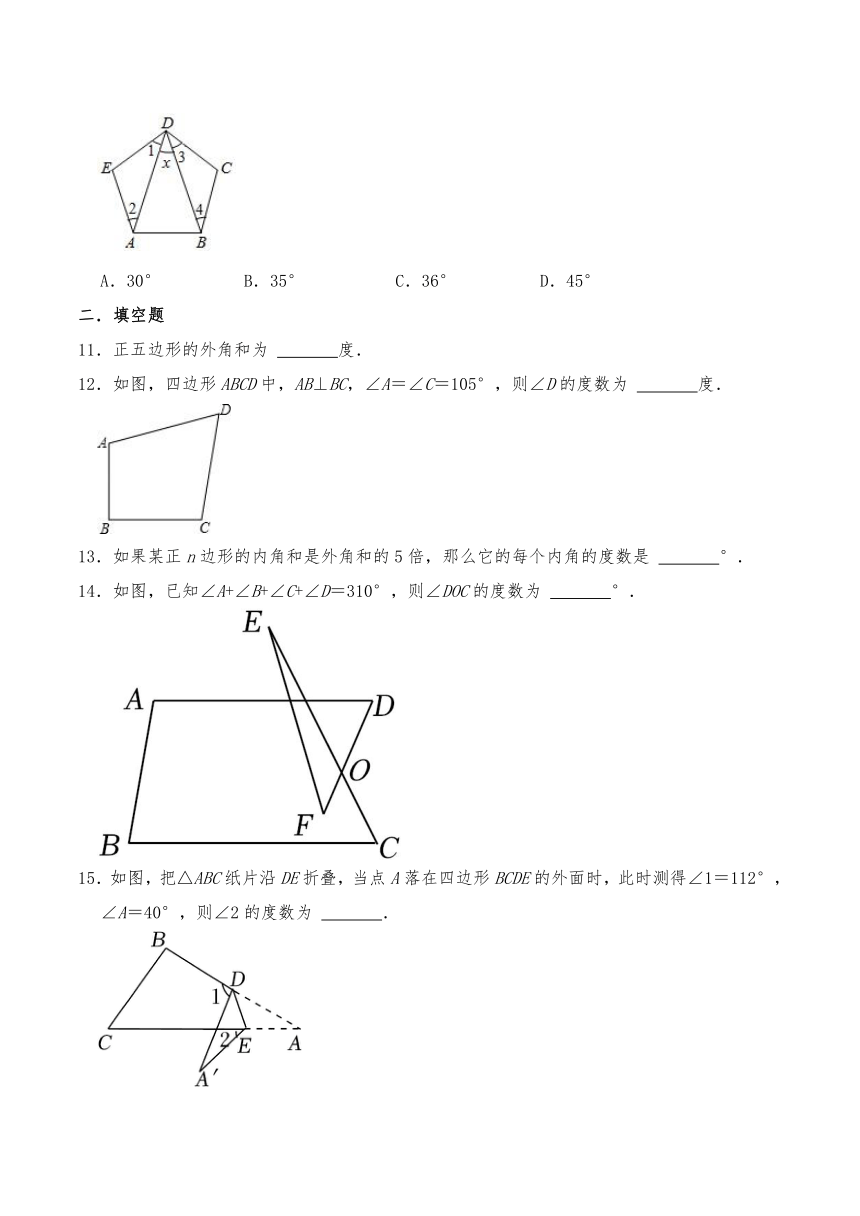
11.正五边形的外角和为 度.
12.如图,四边形ABCD中,AB⊥BC,∠A=∠C=105°,则∠D的度数为 度.
13.如果某正n边形的内角和是外角和的5倍,那么它的每个内角的度数是 °.
14.如图,已知∠A+∠B+∠C+∠D=310°,则∠DOC的度数为 °.
15.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为 .
16.如图,已知∠B=30°,则∠A+∠D+∠C+∠G= °.
三.解答题
17.如图,四边形ABCD中,AB∥CD,BE,CG分别平分∠ABC和∠BCD,且EF∥CG,∠BCD=60°.
(1)求∠ABC的度数;
(2)求∠BEF的度数.
18.看图回答问题:
(1)内角和为2014°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
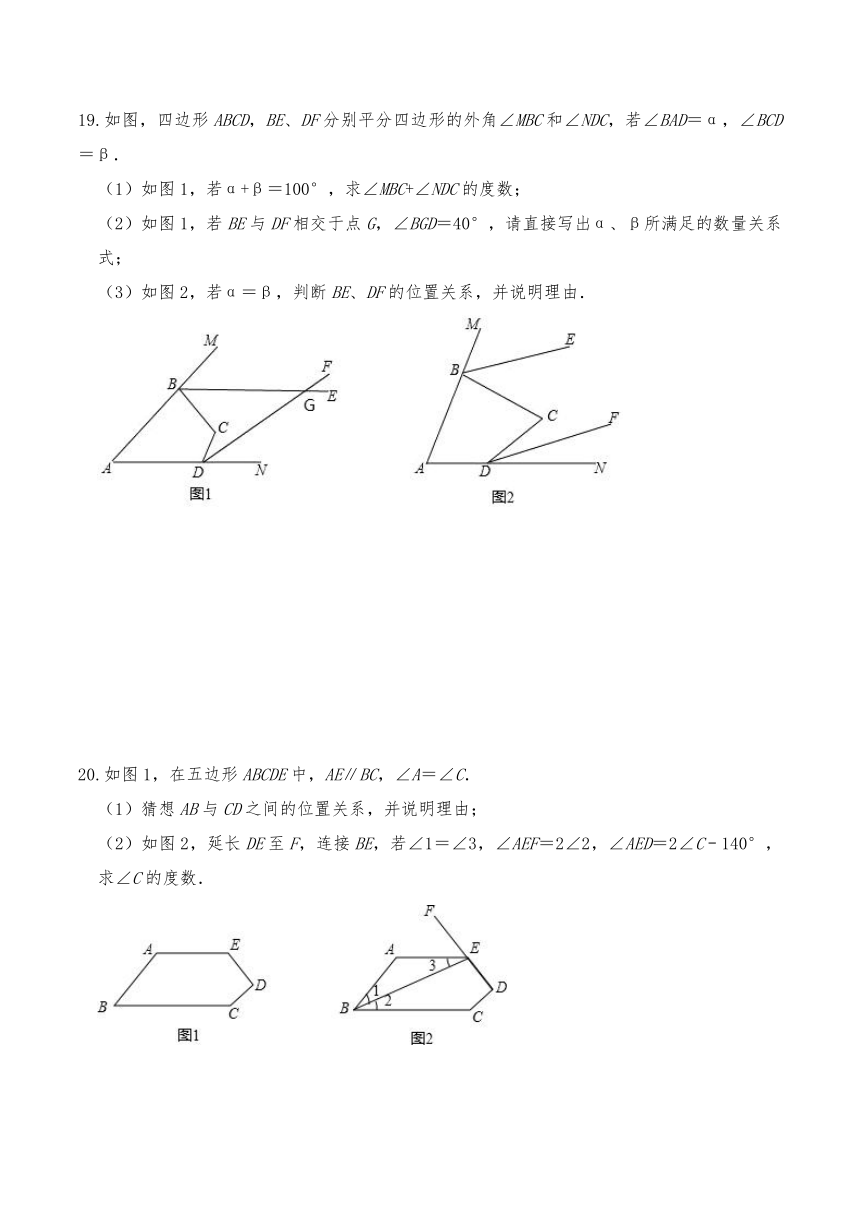
19.如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=100°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=40°,请直接写出α、β所满足的数量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
20.如图1,在五边形ABCDE中,AE∥BC,∠A=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)如图2,延长DE至F,连接BE,若∠1=∠3,∠AEF=2∠2,∠AED=2∠C﹣140°,求∠C的度数.
21.(1)n边形(n>3)其中一个顶点的对角线有 条;
(2)一个凸多边形共有14条对角线,它是几边形?
(3)是否存在有21条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明理由.
22.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)淇淇一共走了多少米?说明理由.
(2)求这个多边形的内角和.
答案
一.选择题
A.A.A.A.A.D.D.C.A.C.
二.填空题
11.360.
12.60.
13.150.
14.130.
15.32°.
16.210.
三.解答题
17.解:(1)∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD﹣60°,
∴∠ABC=120°;
(2)∵BE、CG分别平分∠ABC、∠BCD,
∴∠EBC=∠ABC=60°,∠BCG=∠BCD=30°,
∵EF∥CG,
∴∠BFE=∠BCG=30°,
∵∠BEF+∠EBC+∠BFE=180°,
∴∠BEF=180°﹣60°﹣30°=90°.
18.解:(1)∵n边形的内角和是(n﹣2) 180°,
∴内角和一定是180度的倍数,
∵2014÷180=11…34,
∴内角和为2014°不可能;
(2)依题意有(x﹣2) 180°<2014°,
解得x<13.
因而多边形的边数是13,
故小华求的是十三边形的内角和.
19.解:(1)∵∠ABC+∠ADC=360°﹣(α+β),
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=100°.
(2)β﹣α=80°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°﹣β+40°=180°,
∴β﹣α=80°,
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,
∴∠CBE+β﹣∠DHB=(α+β),
∵α=β,
∴∠CBE+β﹣∠DHB=(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
20.解:(1)猜想:AB∥CD,
理由:∵AE∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD;
(2)∵AE∥BC,
∴∠2=∠3,∠A+∠ABC=180°,
∵∠1=∠3,
∴∠1=∠2=∠3,∠ABC=2∠2,
∵∠AEF=2∠2,
∴∠A+∠ABC=∠A+2∠2=∠A+∠AEF=180°,
∵∠AEF+∠AED=180°,
∴∠A=∠AED,
∵∠A=∠C,
∴∠AED=∠C,
∵∠AED=2∠C﹣140°,
∴∠C=2∠C﹣140°,
解得:∠C=140°.
21.解:(1)n边形过每一个顶点的对角线有(n﹣3)条,
故答案为:(n﹣3);
(2)设它是n边形,
则=14,
即n2﹣3n﹣28=0,
解得:n=7或n=﹣4(舍去),
∴它是七边形;
(3)不存在,
理由如下:如果存在,它是n边形,
则=21,
即n2﹣3n﹣42=0,
解得:n=,
∵n不为正整数,
∴不存在.
22.解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
一.选择题
1.若正多边形的一个内角度数为144°,则这个多边形的边数为( )
A.10 B.12 C.8 D.7
2.一个正多边形的一个内角为90°,则这个正多边形的边数为( )
A.4 B.5 C.6 D.7
3.正八边形比正六边形的每个内角的度数多( )
A.15° B.30° C.45° D.60°
4.下列图中,内角和最小的是( )
A. B.
C. D.
5.一个多边形减去一个角后,所得多边形的内角和是720°,则这个多边形的边数不可能是( )
A.4 B.5 C.6 D.7
6.当多边形的边数增加1时,它的内角和与外角和( )
A.都不变
B.都增加180°
C.内角和增加180°,外角和减少180°
D.内角和增加180°,外角和不变
7.如图,点A1,A2,A3,A4为一个正十二边形相邻的四个顶点,则∠A4A1A2为( )
A.15° B.20° C.25° D.30°
8.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
A.360° B.450° C.540° D.720°
9.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
10.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
二.填空题
11.正五边形的外角和为 度.
12.如图,四边形ABCD中,AB⊥BC,∠A=∠C=105°,则∠D的度数为 度.
13.如果某正n边形的内角和是外角和的5倍,那么它的每个内角的度数是 °.
14.如图,已知∠A+∠B+∠C+∠D=310°,则∠DOC的度数为 °.
15.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为 .
16.如图,已知∠B=30°,则∠A+∠D+∠C+∠G= °.
三.解答题
17.如图,四边形ABCD中,AB∥CD,BE,CG分别平分∠ABC和∠BCD,且EF∥CG,∠BCD=60°.
(1)求∠ABC的度数;
(2)求∠BEF的度数.
18.看图回答问题:
(1)内角和为2014°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
19.如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=100°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=40°,请直接写出α、β所满足的数量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
20.如图1,在五边形ABCDE中,AE∥BC,∠A=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)如图2,延长DE至F,连接BE,若∠1=∠3,∠AEF=2∠2,∠AED=2∠C﹣140°,求∠C的度数.
21.(1)n边形(n>3)其中一个顶点的对角线有 条;
(2)一个凸多边形共有14条对角线,它是几边形?
(3)是否存在有21条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明理由.
22.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)淇淇一共走了多少米?说明理由.
(2)求这个多边形的内角和.
答案
一.选择题
A.A.A.A.A.D.D.C.A.C.
二.填空题
11.360.
12.60.
13.150.
14.130.
15.32°.
16.210.
三.解答题
17.解:(1)∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD﹣60°,
∴∠ABC=120°;
(2)∵BE、CG分别平分∠ABC、∠BCD,
∴∠EBC=∠ABC=60°,∠BCG=∠BCD=30°,
∵EF∥CG,
∴∠BFE=∠BCG=30°,
∵∠BEF+∠EBC+∠BFE=180°,
∴∠BEF=180°﹣60°﹣30°=90°.
18.解:(1)∵n边形的内角和是(n﹣2) 180°,
∴内角和一定是180度的倍数,
∵2014÷180=11…34,
∴内角和为2014°不可能;
(2)依题意有(x﹣2) 180°<2014°,
解得x<13.
因而多边形的边数是13,
故小华求的是十三边形的内角和.
19.解:(1)∵∠ABC+∠ADC=360°﹣(α+β),
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=100°.
(2)β﹣α=80°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°﹣β+40°=180°,
∴β﹣α=80°,
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,
∴∠CBE+β﹣∠DHB=(α+β),
∵α=β,
∴∠CBE+β﹣∠DHB=(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
20.解:(1)猜想:AB∥CD,
理由:∵AE∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD;
(2)∵AE∥BC,
∴∠2=∠3,∠A+∠ABC=180°,
∵∠1=∠3,
∴∠1=∠2=∠3,∠ABC=2∠2,
∵∠AEF=2∠2,
∴∠A+∠ABC=∠A+2∠2=∠A+∠AEF=180°,
∵∠AEF+∠AED=180°,
∴∠A=∠AED,
∵∠A=∠C,
∴∠AED=∠C,
∵∠AED=2∠C﹣140°,
∴∠C=2∠C﹣140°,
解得:∠C=140°.
21.解:(1)n边形过每一个顶点的对角线有(n﹣3)条,
故答案为:(n﹣3);
(2)设它是n边形,
则=14,
即n2﹣3n﹣28=0,
解得:n=7或n=﹣4(舍去),
∴它是七边形;
(3)不存在,
理由如下:如果存在,它是n边形,
则=21,
即n2﹣3n﹣42=0,
解得:n=,
∵n不为正整数,
∴不存在.
22.解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
