思维拓展 数与形综合(试题)数学六年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展 数与形综合(试题)数学六年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 16:03:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:数与形综合(试题)数学六年级上册人教版
一、选择题
1.16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和。下列等式中,符合这一规律的是( )。
A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31
2.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
3.在学校最近进行的乒乓球比赛中,每两个同学之间都要进行一场比赛,共进行了66场比赛,那么这次比赛一共有( )个同学参加。
A.10 B.11 C.12
4.如下图,用同样长的小木棒摆一摆,照这样摆下去,第(7)幅图需要( )根这样的小木棒。
A.28 B.34 C.40 D.46
5.按照下图规律,摆第7个图形需要( )根小棒。
A.21 B.22 C.28
6.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
二、填空题
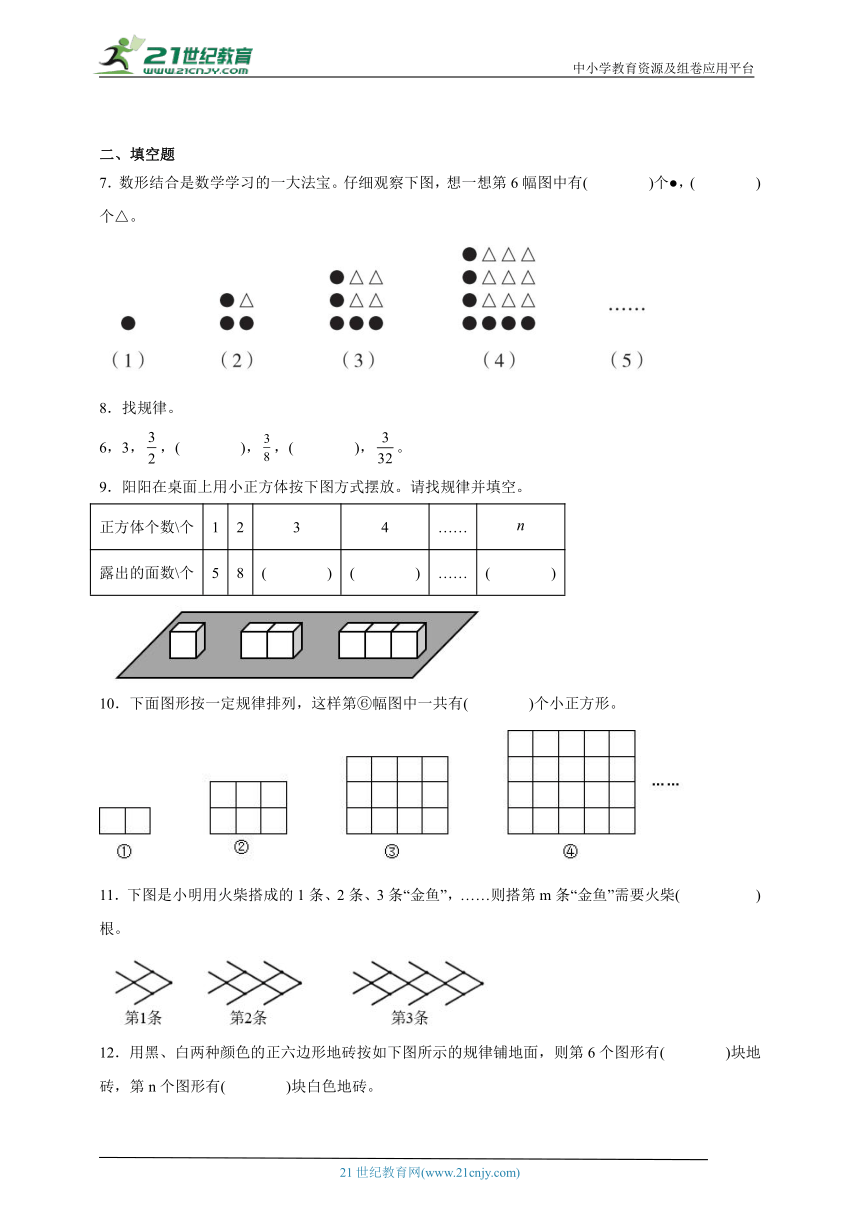
7.数形结合是数学学习的一大法宝。仔细观察下图,想一想第6幅图中有( )个●,( )个△。
8.找规律。
6,3,,( ),,( ),。
9.阳阳在桌面上用小正方体按下图方式摆放。请找规律并填空。
正方体个数\个 1 2 3 4 ……
露出的面数\个 5 8 ( ) ( ) …… ( )
10.下面图形按一定规律排列,这样第⑥幅图中一共有( )个小正方形。
11.下图是小明用火柴搭成的1条、2条、3条“金鱼”,……则搭第m条“金鱼”需要火柴( )根。
12.用黑、白两种颜色的正六边形地砖按如下图所示的规律铺地面,则第6个图形有( )块地砖,第n个图形有( )块白色地砖。
13.将图①中边长为2厘米的正方形复制并向右平移1厘米,得到图②。以后每次得到的正方形这样复制平移,就形成了以下一组图形。
……
第2个图形的周长是( )厘米;第( )个图形的周长是18厘米;第n个图形的周长是( )厘米。
14.先观察下面算式的规律,再填一填。
( )
( )
( )
三、解答题
15.我国宋代数学家杨辉在1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现下面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形图继续写下去吗?试试看。
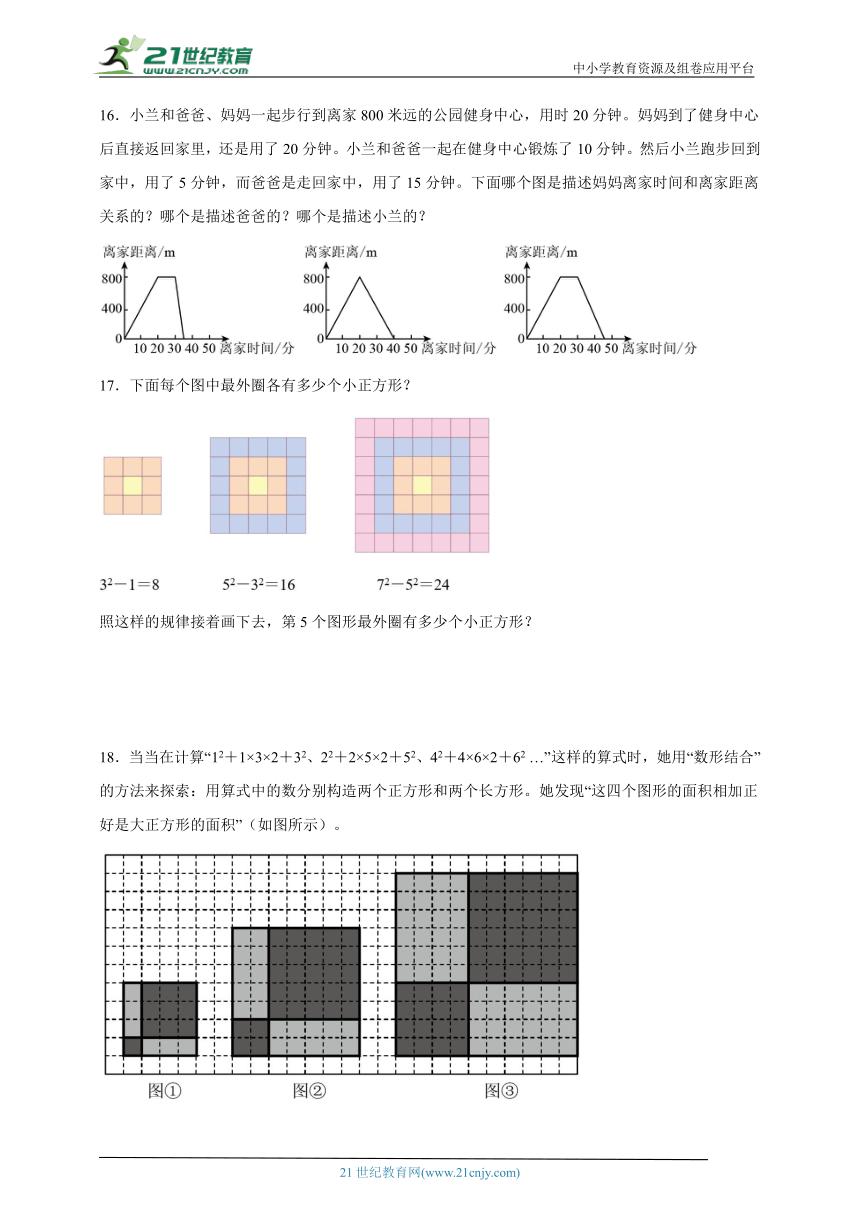
16.小兰和爸爸、妈妈一起步行到离家800米远的公园健身中心,用时20分钟。妈妈到了健身中心后直接返回家里,还是用了20分钟。小兰和爸爸一起在健身中心锻炼了10分钟。然后小兰跑步回到家中,用了5分钟,而爸爸是走回家中,用了15分钟。下面哪个图是描述妈妈离家时间和离家距离关系的?哪个是描述爸爸的?哪个是描述小兰的?
17.下面每个图中最外圈各有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?
18.当当在计算“12+1×3×2+32、22+2×5×2+52、42+4×6×2+62 …”这样的算式时,她用“数形结合”的方法来探索:用算式中的数分别构造两个正方形和两个长方形。她发现“这四个图形的面积相加正好是大正方形的面积”(如图所示)。
由此得出:
图①:12+1×3×2+32=42
图②:22+2×5×2+52=72
图③:42+4×6×2+62=102
(1)根据当当发现的规律填空:
32+3×5×2+52=( )。
162+16×19×2+192=( )。
(2)你能根据当当发现的规律,把如图这个正方形分成四块,并用算式表示出来吗?
( )=92
19.用小棒按照如下方式摆图形,摆一个八边形需要8根小棒。观察规律。
(1)根据规律,怎样摆出4个八边形,把你的想法画在方框内。
(2)照这样画下去,想一想,摆7个八边形需要( )根小棒,如果想摆n个八边形需要( )根小棒。
20.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
参考答案:
1.C
【分析】观察几个图片,可以发现:任何一个大于1的“正方形数”正好等于每个正方形图中,每列点子个数的平方;“三角形数”等于相邻自然数相加的和,可分别总结出每个“正方形数”、“三角形数”的规律,并按此规律继续推理出几个“正方形数”、“三角形数”,再结合选项判断即可。
【详解】图一中:等号左边是4,就是22,也就是这个正方形每列的点子数的平方;等号右边是1+3,是两个相邻“三角形数”之和,因此,可把1看作第一个“三角形数”,1+2=3,3就是第二个“三角形数”;
图二中:32=9=3+6,9是“正方形数”,3是第二个“三角形数”,1+2+3=6,6是第三个“三角形数”;
图三中:42=16=6+10,16是“正方形数”,6是第三个三角形数,1+2+3+4=10,10是第四个“三角形数”;
以此类推:
图四中:应该是52=25=10+15,25是“正方形数”,这里10是第四个“三角形数”,15是第五个“三角形数”;
图五中:应该是62=36=15+21;
图六中:应该是72=49=21+28;
……
A.13=3+10:13不是一个数的平方,也就不是“正方形数”,不合题意;
B.25=9+16:9、16都不是“三角形数”,不合题意;
C.36=15+21:36是6的平方,15和21是相邻的“三角形数”,符合题意;
D.49=18+31:18、31都不是“三角形数”,不合题意。
故答案为:C
【点睛】本题较为复杂,需要运用数形结合的思想,通过观察总结“三角形数”、“正方形数”的规律,并加以应用。
2.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
3.C
【分析】本题属于握手问题,其公式为人数×(人数-1)÷2=比赛次数。设人数为x,则x(x-1)÷2=66,据此求出人数即可。
【详解】x(x-1)÷2=66
则:x(x-1)=132;
A.当x=10时,10×(10-1)=90,不符合;
B.当x=11时,11×(11-1)=110,不符合;
C.当x=12时,12×(12-1)=132,符合;
那么这次比赛一共有(12)个同学参加。
故答案为:C
【点睛】熟练掌握握手问题的公式是解答本题的关键。
4.C
【分析】观察可知,小木棒根数=第几幅图就用几×4+(几-1)×2,据此列式计算。
【详解】7×4+(7-1)×2
=28+6×2
=28+12
=40(根)
第(7)幅图需要40根这样的小木棒。
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.B
【分析】第1个图形需要1+3=4(根)小棒,第2个图形需要1+3×2=7(根)小棒,第3个图形需要1+3×3=10(根)小棒,……由此发现规律:第n个图形需要(1+3n)根小棒。
【详解】1+3×7
=1+21
=22(根)
所以摆第7个图形需要22根小棒。
故答案为:B
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
6.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
7. 11 25
【分析】第几幅图用n表示,观察可知,●的个数=(n-1)×2+1;△的个数=(n-1)2,据此列式计算。
【详解】(6-1)×2+1
=5×2+1
=10+1
=11(个)
(6-1)2
=52
=25(个)
第6幅图中有11个●,25个△。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.
【分析】根据题意可知,6×=3, 3×=,…依次类推,每一个数都是前一个数的;据此解答。
【详解】×=
×=
6,3,,,,,。
【点睛】解答此题的关键是根据所给出的数字,找出规律,再根据规律解决问题。
9. 11 14 3n+2
【分析】观察可知,露出的面数=正方体个数×3+2,据此分析。
【详解】3×3+2
=9+2
=11(个)
4×3+2
=12+2
=14(个)
n×3+2=(3n+2)个
正方体个数\个 1 2 3 4 ……
露出的面数\个 5 8 11 14 …… 3n+2
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
10.42
【分析】观察图形可知:第①幅图中的小正方形一共有1行,每行2个,第②幅图中的小正方形一共有2行,每行3个,第③幅图中的小正方形一共有3行,每行4个,第④幅图中的小正方形一共有4行,每行5个,据此类推,第n幅图中小正方形一共有n行,每行有(n+1)个, 把n=6代入,算出第⑥幅图中一共有多少小正方形即可。
【详解】由分析可知:
6×(6+1)
=6×7
=42(个)
所以第⑥幅图中一共有42个小正方形。
【点睛】本题重点考查数与形的规律,明确行数和列数之间的关系是解答本题的关键。
11.6m+2
【分析】观察图形发现:搭1条金鱼需要火柴8根,搭2条金鱼需要14根,即发现了每多搭l条鱼,需要多用6根火柴,则搭m条“金鱼”需要火柴8+6(m-1)=(6m+2)条, 据此即可解答问题。
【详解】根据分析得,每多搭一条金鱼,需要多用6根火柴。
8+6×(m-1)
=8+6m-6
=(6m+2)根
所以搭m条金鱼需要火柴(6m+2)根。
【点睛】此类题找规律的时候一定要注意结合图形进行发现规律。
12. 32 2+4n
【分析】第1个图形,黑色地砖有1块,白色地砖有2+4=6(块);第2个图形,黑色地砖有2块,白色地砖有2+4×2=10(块);第3个图形,黑色地砖有3块,白色地砖有2+4×3=14(块);……由此发现:第n个图形,黑色地砖有n块,白色地砖有(2+4n)块。第6个图形有6块黑色地砖,有(2+4×6)块白色地砖,二者相加可求出一共的地砖块数。
【详解】6+(2+4×6)
=6+(2+24)
=6+26
=32(块)
所以,第6个图形有32块地砖,第n个图形有(2+4n)块白色地砖。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
13. 10 6 2(n+3)
【分析】根据题意,图中每个小长方形的宽是1厘米。第1个图形正方形的周长=2×4=8(厘米),观察图形可以发现,第2个图形的周长比正方形的周长多了2厘米,是2×4+2=2×5=10(厘米);第3个图形的周长比正方形的周长多了4厘米,是2×4+4=2×6=12(厘米)。以此类推,第n个图形的周长=2(n+3)。
图形的周长是18厘米,则2(n+3)=18,根据等式的性质解出方程即可得出图形的序号。
【详解】2×4+2
=8+2
=10(厘米)
则第2个图形的周长是10厘米;
通过分析,第n个图形的周长是2(n+3)厘米;
2(n+3)=18
解:n+3=18÷2
n+3=9
n=6
则第6个图形的周长是18厘米。
【点睛】本题考查数形结合问题。通过观察、计算和分析,发现图形的周长与序号之间的关系是解题的关键。
14.
【分析】如下图,把正方形看作单位“1”。由图一可知:==;由图二可知:==;由图三可知:==;由图四可知:==;……由此发现规律:一个连加算式,第一个加数是,之后每个加数都是前一个加数的一半,这个算式的结果就是1减去最后一个加数所得的差。
【详解】=
=
=
【点睛】数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。
15.见详解
【分析】观察“杨辉三角”,发现下层中间的数等于上层相邻两个数的和,据此规律解答。
【详解】我发现“杨辉三角”图中各数之间的关系:这些数字组成的三角形是等腰三角形,两条腰上的数都是1,从第3行开始,中间的每一个数都等于它上方相邻的两个数字之和。
按照发现的规律把这个三角形图继续写下去:
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
16.见详解
【分析】折线统计图中,横轴表示离家时间,纵轴表示离家距离,折线越陡表示走路速度越快,需要时间越短;折线越缓表示走路速度越慢,需要时间越长;折线与横轴平行时表示小兰或爸爸在健身房锻炼,据此解答。
【详解】表示小兰步行到离家800米远的公园健身中心,用时20分钟,然后在健身中心锻炼了10分钟,最后跑步回到家中,用了5分钟;
表示妈妈步行到离家800米远的公园健身中心,用时20分钟,然后直接返回家里,用了20分钟;
表示爸爸步行到离家800米远的公园健身中心,用时20分钟,然后在健身中心锻炼了10分钟,最后走回家中,用了15分钟。
【点睛】本题主要考查折线统计图,运用数形结合的思想明确折线统计图中每段折线表示的意义是解答题目的关键。
17.40个
【分析】观察题意可知,图①的最外圈正方形个数=8×1,图②的最外圈正方形个数=8×2,图③的最外圈正方形个数=8×3,……,据此推出图n的最外圈正方形个数=8n,据此可得第5个图形最外圈有多少个小正方形。
【详解】图①的最外圈正方形个数:8=8×1
图②的最外圈正方形个数:16=8×2
图③的最外圈正方形个数:24=8×3
……
图n的最外圈正方形个数:8n
当n=5时,
8n
=8×5
=40(个)
答:第5个图形最外圈有40个小正方形。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
18.(1)82,352
(2)22+2×7×2+72
图见详解
【分析】根据题意,用算式中的数分别构造两个正方形和两个长方形。这四个图形的面积相加正好是大正方形的面积,由此可知:
图①:12+1×3×2+32=(1+3)2=42
图②:22+2×5×2+52=(2+5)2=72
图③:42+4×6×2+62=(4+6)2=102
也就是说a2+2ab+b2=(a+b)2,据此规律解答即可。
【详解】(1)根据当当发现的规律填空:
32+3×5×2+52=(3+5)2=82
162+16×19×2+192=(16+19)2=352
(2)你能根据当当发现的规律,把如图这个正方形分成四块,用算式表示出来如下:
22+2×7×2+72=92;
图如下:
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
19.(1)见详解
(2)50;1+7n
【分析】(1)摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,15=1+2×7,摆3个八边形需要22根小棒,22=1+3×7, 摆n个八边形需要的小棒数为:(1+7n)根,据此解答即可。
【详解】(1)如图所示:
(2)摆7个八边形需要小棒的根数为:
1+7n=1+7×7
=1+49
=50
则摆7个八边形需要50根小棒,如果想摆n个八边形需要(1+7n)根小棒。
【点睛】本题主要考查数.与形结合的规律,发现每多1个八边形就多7根小棒是解本题的关键。
20.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:数与形综合(试题)数学六年级上册人教版
一、选择题
1.16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和。下列等式中,符合这一规律的是( )。
A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31
2.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
3.在学校最近进行的乒乓球比赛中,每两个同学之间都要进行一场比赛,共进行了66场比赛,那么这次比赛一共有( )个同学参加。
A.10 B.11 C.12
4.如下图,用同样长的小木棒摆一摆,照这样摆下去,第(7)幅图需要( )根这样的小木棒。
A.28 B.34 C.40 D.46
5.按照下图规律,摆第7个图形需要( )根小棒。
A.21 B.22 C.28
6.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
二、填空题
7.数形结合是数学学习的一大法宝。仔细观察下图,想一想第6幅图中有( )个●,( )个△。
8.找规律。
6,3,,( ),,( ),。
9.阳阳在桌面上用小正方体按下图方式摆放。请找规律并填空。
正方体个数\个 1 2 3 4 ……
露出的面数\个 5 8 ( ) ( ) …… ( )
10.下面图形按一定规律排列,这样第⑥幅图中一共有( )个小正方形。
11.下图是小明用火柴搭成的1条、2条、3条“金鱼”,……则搭第m条“金鱼”需要火柴( )根。
12.用黑、白两种颜色的正六边形地砖按如下图所示的规律铺地面,则第6个图形有( )块地砖,第n个图形有( )块白色地砖。
13.将图①中边长为2厘米的正方形复制并向右平移1厘米,得到图②。以后每次得到的正方形这样复制平移,就形成了以下一组图形。
……
第2个图形的周长是( )厘米;第( )个图形的周长是18厘米;第n个图形的周长是( )厘米。
14.先观察下面算式的规律,再填一填。
( )
( )
( )
三、解答题
15.我国宋代数学家杨辉在1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现下面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形图继续写下去吗?试试看。
16.小兰和爸爸、妈妈一起步行到离家800米远的公园健身中心,用时20分钟。妈妈到了健身中心后直接返回家里,还是用了20分钟。小兰和爸爸一起在健身中心锻炼了10分钟。然后小兰跑步回到家中,用了5分钟,而爸爸是走回家中,用了15分钟。下面哪个图是描述妈妈离家时间和离家距离关系的?哪个是描述爸爸的?哪个是描述小兰的?
17.下面每个图中最外圈各有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?
18.当当在计算“12+1×3×2+32、22+2×5×2+52、42+4×6×2+62 …”这样的算式时,她用“数形结合”的方法来探索:用算式中的数分别构造两个正方形和两个长方形。她发现“这四个图形的面积相加正好是大正方形的面积”(如图所示)。
由此得出:
图①:12+1×3×2+32=42
图②:22+2×5×2+52=72
图③:42+4×6×2+62=102
(1)根据当当发现的规律填空:
32+3×5×2+52=( )。
162+16×19×2+192=( )。
(2)你能根据当当发现的规律,把如图这个正方形分成四块,并用算式表示出来吗?
( )=92
19.用小棒按照如下方式摆图形,摆一个八边形需要8根小棒。观察规律。
(1)根据规律,怎样摆出4个八边形,把你的想法画在方框内。
(2)照这样画下去,想一想,摆7个八边形需要( )根小棒,如果想摆n个八边形需要( )根小棒。
20.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
参考答案:
1.C
【分析】观察几个图片,可以发现:任何一个大于1的“正方形数”正好等于每个正方形图中,每列点子个数的平方;“三角形数”等于相邻自然数相加的和,可分别总结出每个“正方形数”、“三角形数”的规律,并按此规律继续推理出几个“正方形数”、“三角形数”,再结合选项判断即可。
【详解】图一中:等号左边是4,就是22,也就是这个正方形每列的点子数的平方;等号右边是1+3,是两个相邻“三角形数”之和,因此,可把1看作第一个“三角形数”,1+2=3,3就是第二个“三角形数”;
图二中:32=9=3+6,9是“正方形数”,3是第二个“三角形数”,1+2+3=6,6是第三个“三角形数”;
图三中:42=16=6+10,16是“正方形数”,6是第三个三角形数,1+2+3+4=10,10是第四个“三角形数”;
以此类推:
图四中:应该是52=25=10+15,25是“正方形数”,这里10是第四个“三角形数”,15是第五个“三角形数”;
图五中:应该是62=36=15+21;
图六中:应该是72=49=21+28;
……
A.13=3+10:13不是一个数的平方,也就不是“正方形数”,不合题意;
B.25=9+16:9、16都不是“三角形数”,不合题意;
C.36=15+21:36是6的平方,15和21是相邻的“三角形数”,符合题意;
D.49=18+31:18、31都不是“三角形数”,不合题意。
故答案为:C
【点睛】本题较为复杂,需要运用数形结合的思想,通过观察总结“三角形数”、“正方形数”的规律,并加以应用。
2.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
3.C
【分析】本题属于握手问题,其公式为人数×(人数-1)÷2=比赛次数。设人数为x,则x(x-1)÷2=66,据此求出人数即可。
【详解】x(x-1)÷2=66
则:x(x-1)=132;
A.当x=10时,10×(10-1)=90,不符合;
B.当x=11时,11×(11-1)=110,不符合;
C.当x=12时,12×(12-1)=132,符合;
那么这次比赛一共有(12)个同学参加。
故答案为:C
【点睛】熟练掌握握手问题的公式是解答本题的关键。
4.C
【分析】观察可知,小木棒根数=第几幅图就用几×4+(几-1)×2,据此列式计算。
【详解】7×4+(7-1)×2
=28+6×2
=28+12
=40(根)
第(7)幅图需要40根这样的小木棒。
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.B
【分析】第1个图形需要1+3=4(根)小棒,第2个图形需要1+3×2=7(根)小棒,第3个图形需要1+3×3=10(根)小棒,……由此发现规律:第n个图形需要(1+3n)根小棒。
【详解】1+3×7
=1+21
=22(根)
所以摆第7个图形需要22根小棒。
故答案为:B
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
6.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
7. 11 25
【分析】第几幅图用n表示,观察可知,●的个数=(n-1)×2+1;△的个数=(n-1)2,据此列式计算。
【详解】(6-1)×2+1
=5×2+1
=10+1
=11(个)
(6-1)2
=52
=25(个)
第6幅图中有11个●,25个△。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.
【分析】根据题意可知,6×=3, 3×=,…依次类推,每一个数都是前一个数的;据此解答。
【详解】×=
×=
6,3,,,,,。
【点睛】解答此题的关键是根据所给出的数字,找出规律,再根据规律解决问题。
9. 11 14 3n+2
【分析】观察可知,露出的面数=正方体个数×3+2,据此分析。
【详解】3×3+2
=9+2
=11(个)
4×3+2
=12+2
=14(个)
n×3+2=(3n+2)个
正方体个数\个 1 2 3 4 ……
露出的面数\个 5 8 11 14 …… 3n+2
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
10.42
【分析】观察图形可知:第①幅图中的小正方形一共有1行,每行2个,第②幅图中的小正方形一共有2行,每行3个,第③幅图中的小正方形一共有3行,每行4个,第④幅图中的小正方形一共有4行,每行5个,据此类推,第n幅图中小正方形一共有n行,每行有(n+1)个, 把n=6代入,算出第⑥幅图中一共有多少小正方形即可。
【详解】由分析可知:
6×(6+1)
=6×7
=42(个)
所以第⑥幅图中一共有42个小正方形。
【点睛】本题重点考查数与形的规律,明确行数和列数之间的关系是解答本题的关键。
11.6m+2
【分析】观察图形发现:搭1条金鱼需要火柴8根,搭2条金鱼需要14根,即发现了每多搭l条鱼,需要多用6根火柴,则搭m条“金鱼”需要火柴8+6(m-1)=(6m+2)条, 据此即可解答问题。
【详解】根据分析得,每多搭一条金鱼,需要多用6根火柴。
8+6×(m-1)
=8+6m-6
=(6m+2)根
所以搭m条金鱼需要火柴(6m+2)根。
【点睛】此类题找规律的时候一定要注意结合图形进行发现规律。
12. 32 2+4n
【分析】第1个图形,黑色地砖有1块,白色地砖有2+4=6(块);第2个图形,黑色地砖有2块,白色地砖有2+4×2=10(块);第3个图形,黑色地砖有3块,白色地砖有2+4×3=14(块);……由此发现:第n个图形,黑色地砖有n块,白色地砖有(2+4n)块。第6个图形有6块黑色地砖,有(2+4×6)块白色地砖,二者相加可求出一共的地砖块数。
【详解】6+(2+4×6)
=6+(2+24)
=6+26
=32(块)
所以,第6个图形有32块地砖,第n个图形有(2+4n)块白色地砖。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
13. 10 6 2(n+3)
【分析】根据题意,图中每个小长方形的宽是1厘米。第1个图形正方形的周长=2×4=8(厘米),观察图形可以发现,第2个图形的周长比正方形的周长多了2厘米,是2×4+2=2×5=10(厘米);第3个图形的周长比正方形的周长多了4厘米,是2×4+4=2×6=12(厘米)。以此类推,第n个图形的周长=2(n+3)。
图形的周长是18厘米,则2(n+3)=18,根据等式的性质解出方程即可得出图形的序号。
【详解】2×4+2
=8+2
=10(厘米)
则第2个图形的周长是10厘米;
通过分析,第n个图形的周长是2(n+3)厘米;
2(n+3)=18
解:n+3=18÷2
n+3=9
n=6
则第6个图形的周长是18厘米。
【点睛】本题考查数形结合问题。通过观察、计算和分析,发现图形的周长与序号之间的关系是解题的关键。
14.
【分析】如下图,把正方形看作单位“1”。由图一可知:==;由图二可知:==;由图三可知:==;由图四可知:==;……由此发现规律:一个连加算式,第一个加数是,之后每个加数都是前一个加数的一半,这个算式的结果就是1减去最后一个加数所得的差。
【详解】=
=
=
【点睛】数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。
15.见详解
【分析】观察“杨辉三角”,发现下层中间的数等于上层相邻两个数的和,据此规律解答。
【详解】我发现“杨辉三角”图中各数之间的关系:这些数字组成的三角形是等腰三角形,两条腰上的数都是1,从第3行开始,中间的每一个数都等于它上方相邻的两个数字之和。
按照发现的规律把这个三角形图继续写下去:
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
16.见详解
【分析】折线统计图中,横轴表示离家时间,纵轴表示离家距离,折线越陡表示走路速度越快,需要时间越短;折线越缓表示走路速度越慢,需要时间越长;折线与横轴平行时表示小兰或爸爸在健身房锻炼,据此解答。
【详解】表示小兰步行到离家800米远的公园健身中心,用时20分钟,然后在健身中心锻炼了10分钟,最后跑步回到家中,用了5分钟;
表示妈妈步行到离家800米远的公园健身中心,用时20分钟,然后直接返回家里,用了20分钟;
表示爸爸步行到离家800米远的公园健身中心,用时20分钟,然后在健身中心锻炼了10分钟,最后走回家中,用了15分钟。
【点睛】本题主要考查折线统计图,运用数形结合的思想明确折线统计图中每段折线表示的意义是解答题目的关键。
17.40个
【分析】观察题意可知,图①的最外圈正方形个数=8×1,图②的最外圈正方形个数=8×2,图③的最外圈正方形个数=8×3,……,据此推出图n的最外圈正方形个数=8n,据此可得第5个图形最外圈有多少个小正方形。
【详解】图①的最外圈正方形个数:8=8×1
图②的最外圈正方形个数:16=8×2
图③的最外圈正方形个数:24=8×3
……
图n的最外圈正方形个数:8n
当n=5时,
8n
=8×5
=40(个)
答:第5个图形最外圈有40个小正方形。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
18.(1)82,352
(2)22+2×7×2+72
图见详解
【分析】根据题意,用算式中的数分别构造两个正方形和两个长方形。这四个图形的面积相加正好是大正方形的面积,由此可知:
图①:12+1×3×2+32=(1+3)2=42
图②:22+2×5×2+52=(2+5)2=72
图③:42+4×6×2+62=(4+6)2=102
也就是说a2+2ab+b2=(a+b)2,据此规律解答即可。
【详解】(1)根据当当发现的规律填空:
32+3×5×2+52=(3+5)2=82
162+16×19×2+192=(16+19)2=352
(2)你能根据当当发现的规律,把如图这个正方形分成四块,用算式表示出来如下:
22+2×7×2+72=92;
图如下:
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
19.(1)见详解
(2)50;1+7n
【分析】(1)摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,15=1+2×7,摆3个八边形需要22根小棒,22=1+3×7, 摆n个八边形需要的小棒数为:(1+7n)根,据此解答即可。
【详解】(1)如图所示:
(2)摆7个八边形需要小棒的根数为:
1+7n=1+7×7
=1+49
=50
则摆7个八边形需要50根小棒,如果想摆n个八边形需要(1+7n)根小棒。
【点睛】本题主要考查数.与形结合的规律,发现每多1个八边形就多7根小棒是解本题的关键。
20.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
