思维拓展:多边形的面积综合(试题)数学五年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展:多边形的面积综合(试题)数学五年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:多边形的面积综合(试题)数学五年级上册人教版
一、选择题
1.一堆圆木,堆成梯形状,底层15根,顶层7根,这堆圆木共有( )根。
A.88 B.99 C.105
2.一根铁丝围成一个长方形,再把它拉成一个平行四边形,两个图形的面积( )。
A.面积一样大 B.长方形面积大 C.平行四边形面积大
3.下图中,阴影部分的面积和和空白部分的面积不相等的是( )。
A.B.C.
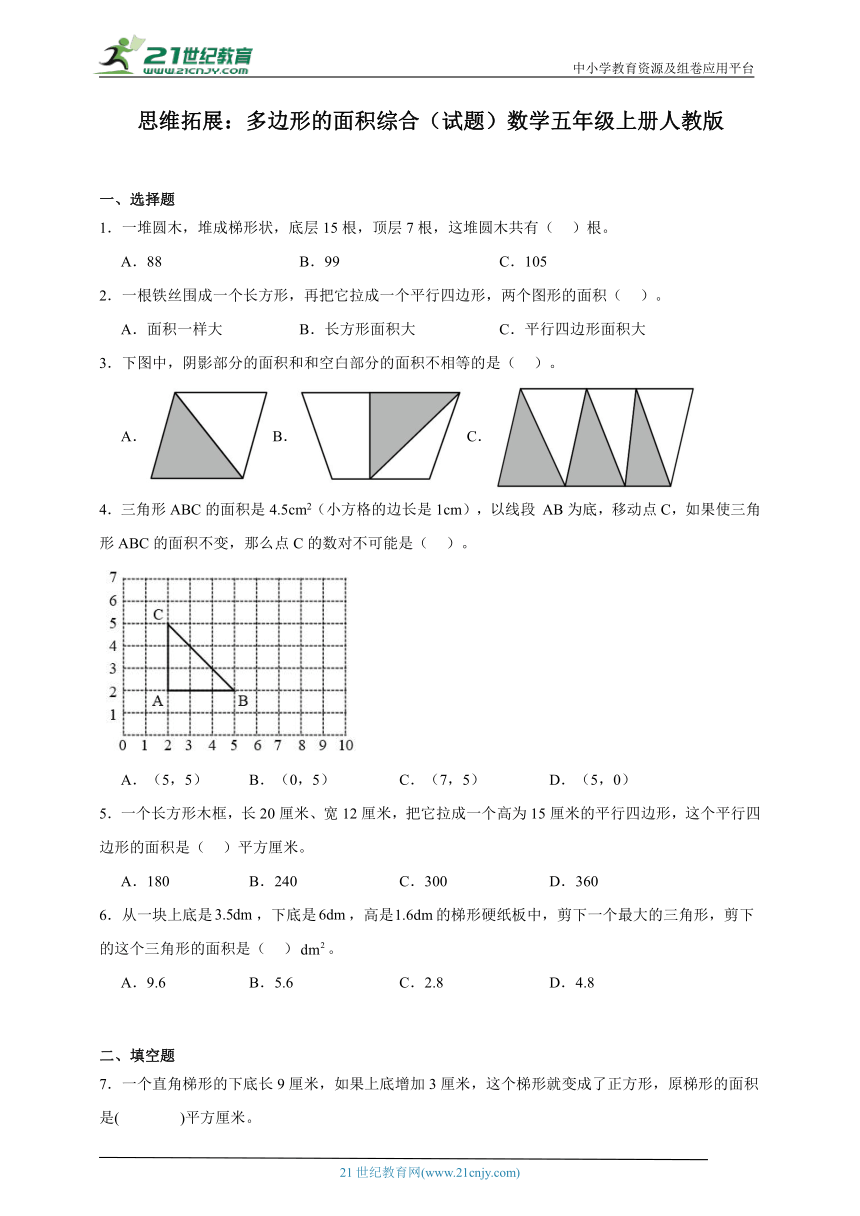
4.三角形ABC的面积是4.5cm2(小方格的边长是1cm),以线段 AB为底,移动点C,如果使三角形ABC的面积不变,那么点C的数对不可能是( )。
A.(5,5) B.(0,5) C.(7,5) D.(5,0)
5.一个长方形木框,长20厘米、宽12厘米,把它拉成一个高为15厘米的平行四边形,这个平行四边形的面积是( )平方厘米。
A.180 B.240 C.300 D.360
6.从一块上底是,下底是,高是的梯形硬纸板中,剪下一个最大的三角形,剪下的这个三角形的面积是( )。
A.9.6 B.5.6 C.2.8 D.4.8
二、填空题
7.一个直角梯形的下底长9厘米,如果上底增加3厘米,这个梯形就变成了正方形,原梯形的面积是( )平方厘米。
8.一个平行四边形的底是13.5dm,高是5.8dm,面积是( ),与它等底等高的三角形的面积是( )。
9.一个直角三角形的三条边分别长6厘米、8厘米、10厘米,直角所对边上的高是( )厘米。
10.一个平行四边形的底是24cm,它的底是高的3倍,它的面积是( )cm2。
11.两个完全一样的梯形可以拼成一个( ),如果拼成图形的面积是90cm2,则一个梯形的面积等于( )cm2。
12.长方形的面积是a平方米,在长方形内画一个最大的三角形,这个三角形的面积是( )平方米。
13.下图是一块不规则的土地,估一估,它的面积大约是( )m2。
14.如图所示,每个小正方形的边长都是2cm,A、B、C是阴影部分三角形的三个顶点,则该三角形的面积是( )cm2。
三、图形计算
15.计算下面图形中阴影部分的面积。
四、解答题
16.给一块底1.6米、高0.9米的三角形广告牌的两面刷油漆。如果每平方米需要油漆0.6千克,共需要多少千克油漆?
17.一个梯形果园,上底是27米,比下底短6米,高是18米。在这个果园种上梨树,如果每棵梨树的占地面积是4平方米,最多可栽梨树多少棵?
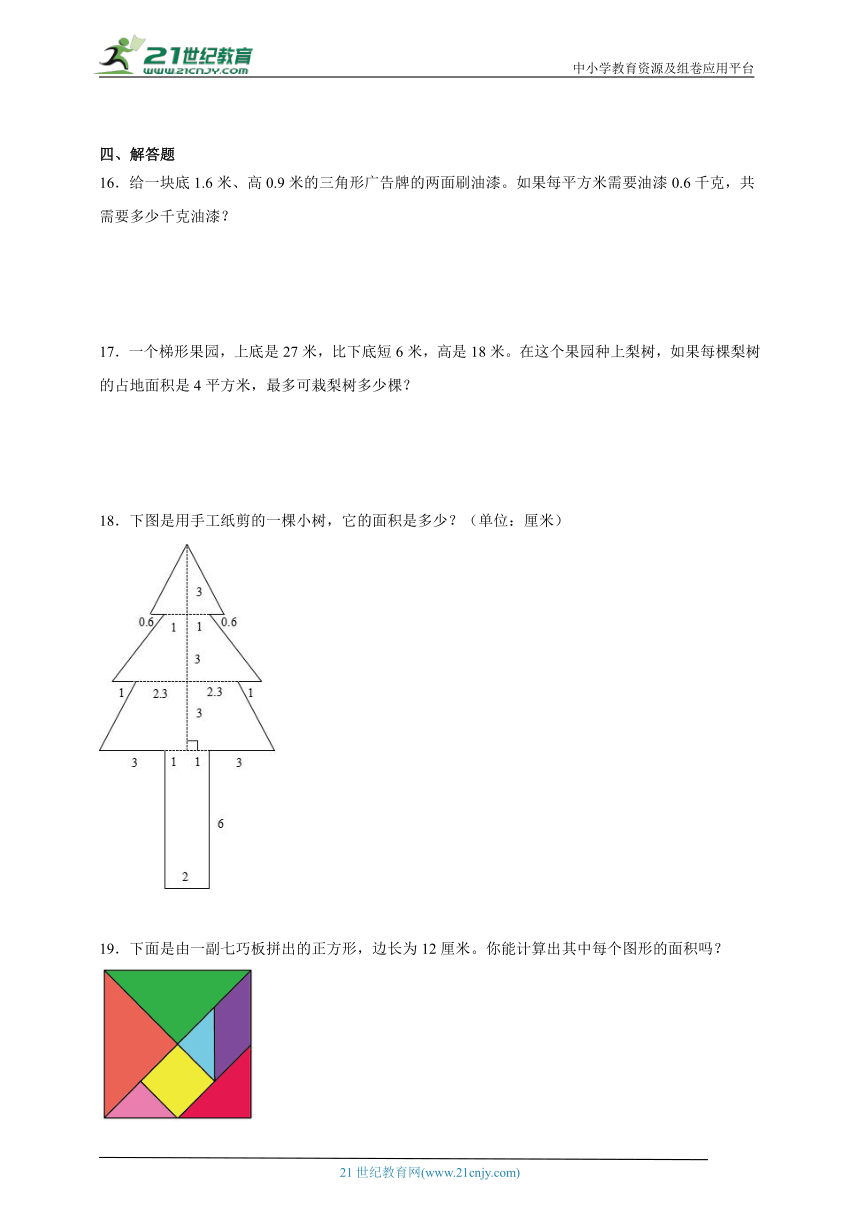
18.下图是用手工纸剪的一棵小树,它的面积是多少?(单位:厘米)
19.下面是由一副七巧板拼出的正方形,边长为12厘米。你能计算出其中每个图形的面积吗?
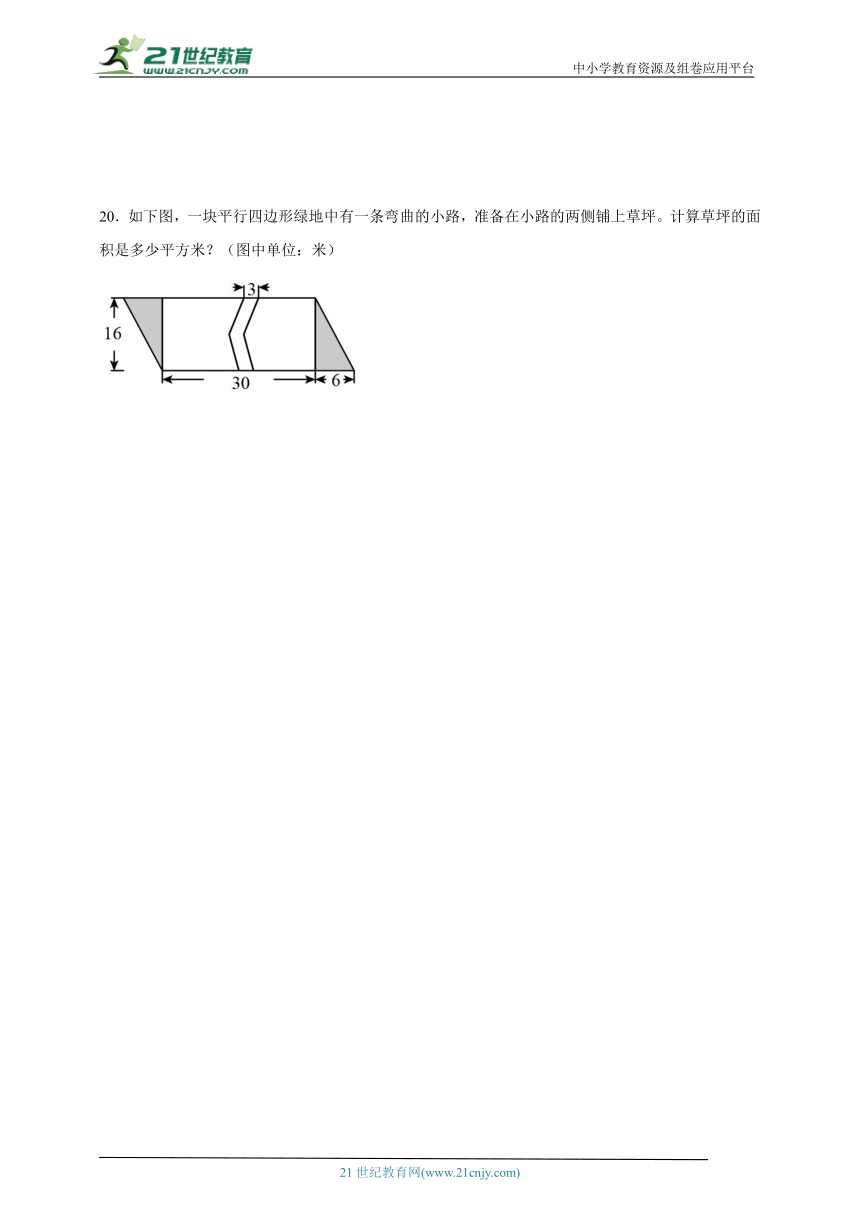
20.如下图,一块平行四边形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪。计算草坪的面积是多少平方米?(图中单位:米)
参考答案:
1.B
【分析】可以把求圆木的根数转化为梯形面积,用下层的根数减去上层的根数加上1就是层数(高),再根据圆木根数=(顶层根数+底层根数)×层数÷2。列式计算即可。
【详解】(7+15)×(15-7+1)÷2
=22×9÷2
=198÷2
=99(根)
则这堆圆木共有99根。
故答案为:B
【点睛】此题主要考查梯形面积公式的灵活运用,关键是求出梯形的高。
2.B
【分析】由于同一根铁丝,说明这两个图形的周长相同,把铁丝拉成平行四边形,长方形的长等于平行四边形的底,宽大于平行四边形的高,长方形的面积=长×宽,平行四边形面积=底×高,分析长方形长和宽与平行四边形底和高之间的关系,即可得出结论。
【详解】长方形的长=平行四边形的底,长方形的宽>平行四边形的高,所以长×宽>底×高,即长方形面积>平行四边形面积,所以长方形面积大。
故答案为:B
【点睛】关键是掌握并灵活运用长方形和平行四边形面积公式。
3.B
【分析】A.把一个平行四边形平均分成两个三角形,这两个三角形的面积相等;
B.阴影部分的面积和和空白部分的面积不相等
C.阴影部分三个三角形的高和空白部分三个三角形的高相等,都是平行四边形的高;阴影部分三个三角形的底合起来就是平行四边形的底,空白部分三个三角形的底合起来也是平行四边形的底,据此可知阴影部分的面积和和空白部分的面积相等。
【详解】阴影部分的面积和和空白部分的面积不相等的是。
故答案为:B
【点睛】明确阴影部分图形和空白部分图形的底和高是解答本题的关键。
4.D
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行。
根据各选项的数对,在图中找到点C移动后的位置,并与点A、B连接起来,组成新的三角形,再与原来三角形ABC相比;如果使三角形ABC的面积不变,那么新三角形和原来的三角形要等底等高,据此解答。
【详解】A.如果点C移动后的位置是(5,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(5,5)。
B.如果点C移动后的位置是(0,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(0,5)。
C.如果点C移动后的位置是(7,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(7,5)。
D.如果点C移动后的位置是(5,0),三角形ABC'与三角形ABC的底相等,但高不相等,所以它们的面积不相等,则移动后点C的数对不可能是(5,0)。
故答案为:D
【点睛】本题考查数对与位置的知识,明确等底等高的三角形面积相等。
5.A
【分析】根据:平行四边形的面积=底×高,把一个长方形木框拉成一个高为15厘米的平行四边形,那么平行四边形的底是12厘米,再根据公式计算出面积即可。
【详解】15×12=180(平方厘米)
所以,这个平行四边形的面积是180平方厘米。
故答案为:A
【点睛】此题考查了平面图形的转化以及平行四边形的面积计算。
6.D
【分析】在梯形硬纸板中剪一个面积最大的三角形,三角形的底等于梯形的下底,高等于梯形的高,根据三角形的面积公式:S=ah÷2,列式计算即可求解。
【详解】6×1.6÷2
=9.6÷2
=4.8(dm2)
即剪下的这个三角形的面积是4.8dm2。
故答案为:D
【点睛】本题考查三角形面积公式的运用,确定梯形中最大三角形的底与高是解题的关键。
7.67.5
【分析】如果上底增加3厘米,这个梯形就变成了正方形,说明这个梯形的高=下底,下底-3=上底,根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(9-3+9)×9÷2
=15×9÷2
=67.5(平方厘米)
原梯形的面积是67.5平方厘米。
【点睛】关键是熟悉梯形的特征,掌握并灵活运用梯形面积公式。
8. 78.3 39.15
【分析】根据平行四边形的面积公式:S=ah,据此代入数值进行计算即可;与平行四边形等底等高的三角形的面积是平行四边形的面积的一半,据此解答 。
【详解】13.5×5.8=78.3(dm2)
78.3÷2=39.15(dm2)
则一个平行四边形的底是13.5dm,高是5.8dm,面积是78.3,与它等底等高的三角形的面积是39.15。
【点睛】本题考查平行四边形和三角形的面积,明确与平行四边形等底等高的三角形的面积是平行四边形的面积的一半是解题的关键。
9.4.8
【分析】直角三角形较短的两条边是两直角边,两直角边可以看作一组底和高,根据三角形面积=底×高÷2,求出三角形面积,三角形面积×2÷直角所对边长=直角所对边上的高。
【详解】6×8÷2=24(平方厘米)
24×2÷10=4.8(厘米)
直角所对边上的高是4.8厘米。
【点睛】关键是熟悉直角三角形特点,掌握并灵活运用三角形面积公式。
10.192
【分析】根据已知一个数的几倍是多少,求这个数用除法计算。求出平行四边形的高。平行四边形的面积=底×高。据此解答。
【详解】24÷3×24=192(cm2)
一个平行四边形的底是24cm,它的底是高的3倍,它的面积是192cm2。
【点睛】本题主要考查平行四边形的面积公式。
11. 平行四边形 45
【分析】根据题意,两个完全一样的梯形通过平移、旋转,可以拼成一个梯形;
因为两个梯形完全一样,那么一个梯形的面积就是拼成的平行四边形面积的一半,据此解答。
【详解】如图:
两个完全一样的梯形可以拼成一个平行四边形。
90÷2=45(cm2)
一个梯形的面积等于45cm2。
【点睛】本题考查转化思想在数学中的应用,明白转化过程中,梯形和平行四边形的面积关系,利用平行四边形的面积求出梯形的面积。
12.0.5a
【分析】在长方形内画一个最大的三角形,那么这个三角形的底等于长方形的长,高等于长方形的宽,根据三角形的面积=底×高÷2,长方形的面积=长×宽,可知这个三角形的面积等于长方形面积的一半,据此解答。
【详解】如图:
a÷2=0.5a(平方米)
这个三角形的面积是0.5a平方米。
【点睛】理解长方形和三角形的面积之间的关系,再用含字母的式子表示三角形的面积。
13.1400
【分析】观察图形可知,这个不规则的土地近似梯形,上底是2个方格,下底是5个方格,高是4个方格,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出方格的总个数;
每个方格是边长为10m的正方形,根据正方形的面积=边长×边长,求出每个方格的面积;
用每个方格的面积乘方格的总个数,即可求出这块不规则土地的面积。
【详解】
一个方格的面积:10×10=100(m2)
方格的总个数:
(2+5)×4÷2
=7×4÷2
=14(个)
总面积:100×14=1400(m2)
它的面积大约是1400m2。
(答案不唯一)
【点睛】掌握不规则图形面积的计算方法是解题的关键,方法一:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量;方法二:把不规则图形分割成学过的规则图形,再用规则图形的面积公式求解。
14.22
【分析】如图,三角形面积=大长方形面积-3个空白三角形的面积,长方形面积=长×宽,三角形面积=底×高÷2,据此列式计算。
【详解】4×2=8(cm)
3×2=6(cm)
2×2=4(cm)
1×2=2(cm)
8×6-6×2÷2-6×4÷2-8×2÷2
=48-6-12-8
=22(cm2)
该三角形的面积是22cm2。
【点睛】关键是掌握并灵活运用长方形和三角形面积公式。
15.18dm2;20m2
【分析】观察图形一,阴影部分的面积就是底为(18-15)dm,高为12dm的三角形的面积,根据三角形的面积公式:S=ah÷2,据此进行计算即可;观察图形二可知,阴影部分的面积等于梯形的面积减去两个空白三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】(18-15)×12÷2
=3×12÷2
=36÷2
=18(dm2)
第一个阴影部分的面积是18dm2。
(5+10)×6÷2-5×2÷2-10×(6-2)÷2
=15×6÷2-5×2÷2-10×4÷2
=45-5-20
=40-20
=20(m2)
第二个阴影部分的面积是20m2。
16.千克
【分析】根据三角形的面积公式:S=ah÷2,据此求出三角形广告牌的面积,再乘2就是需要刷油漆的面积,再用需要刷油漆的面积乘每平方米需要油漆的重量即可求解。
【详解】
=1.44÷2×2×0.6
=0.72×2×0.6
=1.44×0.6
=0.864(千克)
答:共需要0.864千克油漆。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
17.135棵
【分析】由题意可知,一个梯形果园,上底是27米,比下底短6米,则下底是(27+6)米,然后根据梯形的面积公式:S=(a+b)h÷2,据此求出果园的面积,再用果园的面积除以每棵梨树的占地面积即可求解。
【详解】
=60×18÷2÷4
=1080÷2÷4
=540÷4
=135(棵)
答:最多可栽梨树135棵。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
18.48.6平方厘米
【分析】剪纸小树的面积=三角形面积+梯形面积+梯形面积+长方形面积,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,据此列式解答。
【详解】(1×2+0.6×2)×3÷2
=(2+1.2)×3÷2
=3.2×3÷2
=4.8(平方厘米)
(1×2+2.3×2+1×2)×3÷2
=(2+4.6+2)×3÷2
=8.6×3÷2
=12.9(平方厘米)
(2.3×2+3×2+1×2)×3÷2
=(4.6+6+2)×3÷2
=(4.6+6+2)×3÷2
=12.6×3÷2
=18.9(平方厘米)
6×2=12(平方厘米)
4.8+12.9+18.9+12=48.6(平方厘米)
答:它的面积是48.6平方厘米。
【点睛】关键是掌握并灵活运用三角形、梯形和长方形面积公式。
19.见详解
【分析】由图可知,①和②的形状相同面积相等,①和②的面积和等于整个正方形面积的一半;③的底和高都等于正方形边长的一半,利用“三角形的面积=底×高÷2”求出③的面积;④和⑤的形状相同面积相等,都等于③面积的一半;④和⑤可以拼成图形⑥,则⑥的面积等于④或⑤面积的2倍;⑦和⑤等底等高,当三角形和平行四边形等底等高时,三角形的面积是平行四边形面积的一半,平行四边形的面积是三角形面积的2倍,据此解答。
【详解】①或②的面积:12×12÷2÷2
=144÷2÷2
=72÷2
=36(平方厘米)
③的面积:(12÷2)×(12÷2)÷2
=6×6÷2
=36÷2
=18(平方厘米)
④和⑤的面积:18÷2=9(平方厘米)
⑥的面积:9×2=18(平方厘米)
⑦的面积:9×2=18(平方厘米)
【点睛】根据图形分析各图形面积之间的关系并掌握正方形、三角形、平行四边形的面积计算公式是解答题目的关键。
20.528平方米
【分析】观察图形可知,草坪的面积=绿地的面积-小路的面积;其中绿地是一个底为(30+6)米、高为16米的平行四边形;弯曲的小路是2个一样的小平行四边形,可以组成一个底为3米、高为16米的平行四边形;根据平行四边形的面积=底×高,代入数据计算求解。
【详解】绿地的面积:
(30+6)×16
=36×16
=576(平方米)
小路的面积:
3×16=48(平方米)
草坪的面积:
576-48=528(平方米)
答:草坪的面积是528平方米。
【点睛】本题考查平行四边形面积公式的运用,关键是分析出组合图形的面积是由哪些图形的面积相加或相减得到,再运用图形面积公式列式计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:多边形的面积综合(试题)数学五年级上册人教版
一、选择题
1.一堆圆木,堆成梯形状,底层15根,顶层7根,这堆圆木共有( )根。
A.88 B.99 C.105
2.一根铁丝围成一个长方形,再把它拉成一个平行四边形,两个图形的面积( )。
A.面积一样大 B.长方形面积大 C.平行四边形面积大
3.下图中,阴影部分的面积和和空白部分的面积不相等的是( )。
A.B.C.
4.三角形ABC的面积是4.5cm2(小方格的边长是1cm),以线段 AB为底,移动点C,如果使三角形ABC的面积不变,那么点C的数对不可能是( )。
A.(5,5) B.(0,5) C.(7,5) D.(5,0)
5.一个长方形木框,长20厘米、宽12厘米,把它拉成一个高为15厘米的平行四边形,这个平行四边形的面积是( )平方厘米。
A.180 B.240 C.300 D.360
6.从一块上底是,下底是,高是的梯形硬纸板中,剪下一个最大的三角形,剪下的这个三角形的面积是( )。
A.9.6 B.5.6 C.2.8 D.4.8
二、填空题
7.一个直角梯形的下底长9厘米,如果上底增加3厘米,这个梯形就变成了正方形,原梯形的面积是( )平方厘米。
8.一个平行四边形的底是13.5dm,高是5.8dm,面积是( ),与它等底等高的三角形的面积是( )。
9.一个直角三角形的三条边分别长6厘米、8厘米、10厘米,直角所对边上的高是( )厘米。
10.一个平行四边形的底是24cm,它的底是高的3倍,它的面积是( )cm2。
11.两个完全一样的梯形可以拼成一个( ),如果拼成图形的面积是90cm2,则一个梯形的面积等于( )cm2。
12.长方形的面积是a平方米,在长方形内画一个最大的三角形,这个三角形的面积是( )平方米。
13.下图是一块不规则的土地,估一估,它的面积大约是( )m2。
14.如图所示,每个小正方形的边长都是2cm,A、B、C是阴影部分三角形的三个顶点,则该三角形的面积是( )cm2。
三、图形计算
15.计算下面图形中阴影部分的面积。
四、解答题
16.给一块底1.6米、高0.9米的三角形广告牌的两面刷油漆。如果每平方米需要油漆0.6千克,共需要多少千克油漆?
17.一个梯形果园,上底是27米,比下底短6米,高是18米。在这个果园种上梨树,如果每棵梨树的占地面积是4平方米,最多可栽梨树多少棵?
18.下图是用手工纸剪的一棵小树,它的面积是多少?(单位:厘米)
19.下面是由一副七巧板拼出的正方形,边长为12厘米。你能计算出其中每个图形的面积吗?
20.如下图,一块平行四边形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪。计算草坪的面积是多少平方米?(图中单位:米)
参考答案:
1.B
【分析】可以把求圆木的根数转化为梯形面积,用下层的根数减去上层的根数加上1就是层数(高),再根据圆木根数=(顶层根数+底层根数)×层数÷2。列式计算即可。
【详解】(7+15)×(15-7+1)÷2
=22×9÷2
=198÷2
=99(根)
则这堆圆木共有99根。
故答案为:B
【点睛】此题主要考查梯形面积公式的灵活运用,关键是求出梯形的高。
2.B
【分析】由于同一根铁丝,说明这两个图形的周长相同,把铁丝拉成平行四边形,长方形的长等于平行四边形的底,宽大于平行四边形的高,长方形的面积=长×宽,平行四边形面积=底×高,分析长方形长和宽与平行四边形底和高之间的关系,即可得出结论。
【详解】长方形的长=平行四边形的底,长方形的宽>平行四边形的高,所以长×宽>底×高,即长方形面积>平行四边形面积,所以长方形面积大。
故答案为:B
【点睛】关键是掌握并灵活运用长方形和平行四边形面积公式。
3.B
【分析】A.把一个平行四边形平均分成两个三角形,这两个三角形的面积相等;
B.阴影部分的面积和和空白部分的面积不相等
C.阴影部分三个三角形的高和空白部分三个三角形的高相等,都是平行四边形的高;阴影部分三个三角形的底合起来就是平行四边形的底,空白部分三个三角形的底合起来也是平行四边形的底,据此可知阴影部分的面积和和空白部分的面积相等。
【详解】阴影部分的面积和和空白部分的面积不相等的是。
故答案为:B
【点睛】明确阴影部分图形和空白部分图形的底和高是解答本题的关键。
4.D
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行。
根据各选项的数对,在图中找到点C移动后的位置,并与点A、B连接起来,组成新的三角形,再与原来三角形ABC相比;如果使三角形ABC的面积不变,那么新三角形和原来的三角形要等底等高,据此解答。
【详解】A.如果点C移动后的位置是(5,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(5,5)。
B.如果点C移动后的位置是(0,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(0,5)。
C.如果点C移动后的位置是(7,5),三角形ABC'与三角形ABC等底等高,那么它们的面积相等,则移动后点C的数对可能是(7,5)。
D.如果点C移动后的位置是(5,0),三角形ABC'与三角形ABC的底相等,但高不相等,所以它们的面积不相等,则移动后点C的数对不可能是(5,0)。
故答案为:D
【点睛】本题考查数对与位置的知识,明确等底等高的三角形面积相等。
5.A
【分析】根据:平行四边形的面积=底×高,把一个长方形木框拉成一个高为15厘米的平行四边形,那么平行四边形的底是12厘米,再根据公式计算出面积即可。
【详解】15×12=180(平方厘米)
所以,这个平行四边形的面积是180平方厘米。
故答案为:A
【点睛】此题考查了平面图形的转化以及平行四边形的面积计算。
6.D
【分析】在梯形硬纸板中剪一个面积最大的三角形,三角形的底等于梯形的下底,高等于梯形的高,根据三角形的面积公式:S=ah÷2,列式计算即可求解。
【详解】6×1.6÷2
=9.6÷2
=4.8(dm2)
即剪下的这个三角形的面积是4.8dm2。
故答案为:D
【点睛】本题考查三角形面积公式的运用,确定梯形中最大三角形的底与高是解题的关键。
7.67.5
【分析】如果上底增加3厘米,这个梯形就变成了正方形,说明这个梯形的高=下底,下底-3=上底,根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(9-3+9)×9÷2
=15×9÷2
=67.5(平方厘米)
原梯形的面积是67.5平方厘米。
【点睛】关键是熟悉梯形的特征,掌握并灵活运用梯形面积公式。
8. 78.3 39.15
【分析】根据平行四边形的面积公式:S=ah,据此代入数值进行计算即可;与平行四边形等底等高的三角形的面积是平行四边形的面积的一半,据此解答 。
【详解】13.5×5.8=78.3(dm2)
78.3÷2=39.15(dm2)
则一个平行四边形的底是13.5dm,高是5.8dm,面积是78.3,与它等底等高的三角形的面积是39.15。
【点睛】本题考查平行四边形和三角形的面积,明确与平行四边形等底等高的三角形的面积是平行四边形的面积的一半是解题的关键。
9.4.8
【分析】直角三角形较短的两条边是两直角边,两直角边可以看作一组底和高,根据三角形面积=底×高÷2,求出三角形面积,三角形面积×2÷直角所对边长=直角所对边上的高。
【详解】6×8÷2=24(平方厘米)
24×2÷10=4.8(厘米)
直角所对边上的高是4.8厘米。
【点睛】关键是熟悉直角三角形特点,掌握并灵活运用三角形面积公式。
10.192
【分析】根据已知一个数的几倍是多少,求这个数用除法计算。求出平行四边形的高。平行四边形的面积=底×高。据此解答。
【详解】24÷3×24=192(cm2)
一个平行四边形的底是24cm,它的底是高的3倍,它的面积是192cm2。
【点睛】本题主要考查平行四边形的面积公式。
11. 平行四边形 45
【分析】根据题意,两个完全一样的梯形通过平移、旋转,可以拼成一个梯形;
因为两个梯形完全一样,那么一个梯形的面积就是拼成的平行四边形面积的一半,据此解答。
【详解】如图:
两个完全一样的梯形可以拼成一个平行四边形。
90÷2=45(cm2)
一个梯形的面积等于45cm2。
【点睛】本题考查转化思想在数学中的应用,明白转化过程中,梯形和平行四边形的面积关系,利用平行四边形的面积求出梯形的面积。
12.0.5a
【分析】在长方形内画一个最大的三角形,那么这个三角形的底等于长方形的长,高等于长方形的宽,根据三角形的面积=底×高÷2,长方形的面积=长×宽,可知这个三角形的面积等于长方形面积的一半,据此解答。
【详解】如图:
a÷2=0.5a(平方米)
这个三角形的面积是0.5a平方米。
【点睛】理解长方形和三角形的面积之间的关系,再用含字母的式子表示三角形的面积。
13.1400
【分析】观察图形可知,这个不规则的土地近似梯形,上底是2个方格,下底是5个方格,高是4个方格,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出方格的总个数;
每个方格是边长为10m的正方形,根据正方形的面积=边长×边长,求出每个方格的面积;
用每个方格的面积乘方格的总个数,即可求出这块不规则土地的面积。
【详解】
一个方格的面积:10×10=100(m2)
方格的总个数:
(2+5)×4÷2
=7×4÷2
=14(个)
总面积:100×14=1400(m2)
它的面积大约是1400m2。
(答案不唯一)
【点睛】掌握不规则图形面积的计算方法是解题的关键,方法一:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量;方法二:把不规则图形分割成学过的规则图形,再用规则图形的面积公式求解。
14.22
【分析】如图,三角形面积=大长方形面积-3个空白三角形的面积,长方形面积=长×宽,三角形面积=底×高÷2,据此列式计算。
【详解】4×2=8(cm)
3×2=6(cm)
2×2=4(cm)
1×2=2(cm)
8×6-6×2÷2-6×4÷2-8×2÷2
=48-6-12-8
=22(cm2)
该三角形的面积是22cm2。
【点睛】关键是掌握并灵活运用长方形和三角形面积公式。
15.18dm2;20m2
【分析】观察图形一,阴影部分的面积就是底为(18-15)dm,高为12dm的三角形的面积,根据三角形的面积公式:S=ah÷2,据此进行计算即可;观察图形二可知,阴影部分的面积等于梯形的面积减去两个空白三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】(18-15)×12÷2
=3×12÷2
=36÷2
=18(dm2)
第一个阴影部分的面积是18dm2。
(5+10)×6÷2-5×2÷2-10×(6-2)÷2
=15×6÷2-5×2÷2-10×4÷2
=45-5-20
=40-20
=20(m2)
第二个阴影部分的面积是20m2。
16.千克
【分析】根据三角形的面积公式:S=ah÷2,据此求出三角形广告牌的面积,再乘2就是需要刷油漆的面积,再用需要刷油漆的面积乘每平方米需要油漆的重量即可求解。
【详解】
=1.44÷2×2×0.6
=0.72×2×0.6
=1.44×0.6
=0.864(千克)
答:共需要0.864千克油漆。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
17.135棵
【分析】由题意可知,一个梯形果园,上底是27米,比下底短6米,则下底是(27+6)米,然后根据梯形的面积公式:S=(a+b)h÷2,据此求出果园的面积,再用果园的面积除以每棵梨树的占地面积即可求解。
【详解】
=60×18÷2÷4
=1080÷2÷4
=540÷4
=135(棵)
答:最多可栽梨树135棵。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
18.48.6平方厘米
【分析】剪纸小树的面积=三角形面积+梯形面积+梯形面积+长方形面积,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,据此列式解答。
【详解】(1×2+0.6×2)×3÷2
=(2+1.2)×3÷2
=3.2×3÷2
=4.8(平方厘米)
(1×2+2.3×2+1×2)×3÷2
=(2+4.6+2)×3÷2
=8.6×3÷2
=12.9(平方厘米)
(2.3×2+3×2+1×2)×3÷2
=(4.6+6+2)×3÷2
=(4.6+6+2)×3÷2
=12.6×3÷2
=18.9(平方厘米)
6×2=12(平方厘米)
4.8+12.9+18.9+12=48.6(平方厘米)
答:它的面积是48.6平方厘米。
【点睛】关键是掌握并灵活运用三角形、梯形和长方形面积公式。
19.见详解
【分析】由图可知,①和②的形状相同面积相等,①和②的面积和等于整个正方形面积的一半;③的底和高都等于正方形边长的一半,利用“三角形的面积=底×高÷2”求出③的面积;④和⑤的形状相同面积相等,都等于③面积的一半;④和⑤可以拼成图形⑥,则⑥的面积等于④或⑤面积的2倍;⑦和⑤等底等高,当三角形和平行四边形等底等高时,三角形的面积是平行四边形面积的一半,平行四边形的面积是三角形面积的2倍,据此解答。
【详解】①或②的面积:12×12÷2÷2
=144÷2÷2
=72÷2
=36(平方厘米)
③的面积:(12÷2)×(12÷2)÷2
=6×6÷2
=36÷2
=18(平方厘米)
④和⑤的面积:18÷2=9(平方厘米)
⑥的面积:9×2=18(平方厘米)
⑦的面积:9×2=18(平方厘米)
【点睛】根据图形分析各图形面积之间的关系并掌握正方形、三角形、平行四边形的面积计算公式是解答题目的关键。
20.528平方米
【分析】观察图形可知,草坪的面积=绿地的面积-小路的面积;其中绿地是一个底为(30+6)米、高为16米的平行四边形;弯曲的小路是2个一样的小平行四边形,可以组成一个底为3米、高为16米的平行四边形;根据平行四边形的面积=底×高,代入数据计算求解。
【详解】绿地的面积:
(30+6)×16
=36×16
=576(平方米)
小路的面积:
3×16=48(平方米)
草坪的面积:
576-48=528(平方米)
答:草坪的面积是528平方米。
【点睛】本题考查平行四边形面积公式的运用,关键是分析出组合图形的面积是由哪些图形的面积相加或相减得到,再运用图形面积公式列式计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
