北师大版八年级数学上册:1.2一定是直角三角形吗?同步练习 (无答案)
文档属性
| 名称 | 北师大版八年级数学上册:1.2一定是直角三角形吗?同步练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 16:59:11 | ||
图片预览

文档简介
1.2一定是直角三角形吗
一、单选题
1.《九章算术》中有一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?”题意是:有一个水池,水面是一个边长为10尺的正方形,在水池的正中央有一根芦苇,高出水面部分为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的(如图),则水深和芦苇长各多少尺?若设这根芦苇的长度为x尺,根据题意,所列方程正确的是( )
A. B.
C. D.
2.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
3.下列各组数中,是勾股数的是( )
A.7,8,9 B.6,8,11 C.5,12,14 D.3,4,5
4.下列四组线段中,能组成直角三角形的是( )
A.a=2,b=4,c=6 B.a=4,b=6,c=8
C.a=4,b=8,c=10 D.a=6,b=8,c=10
5.如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为,大正方形边长为,则一个直角三角形的面积等于( )
A. B. C. D.
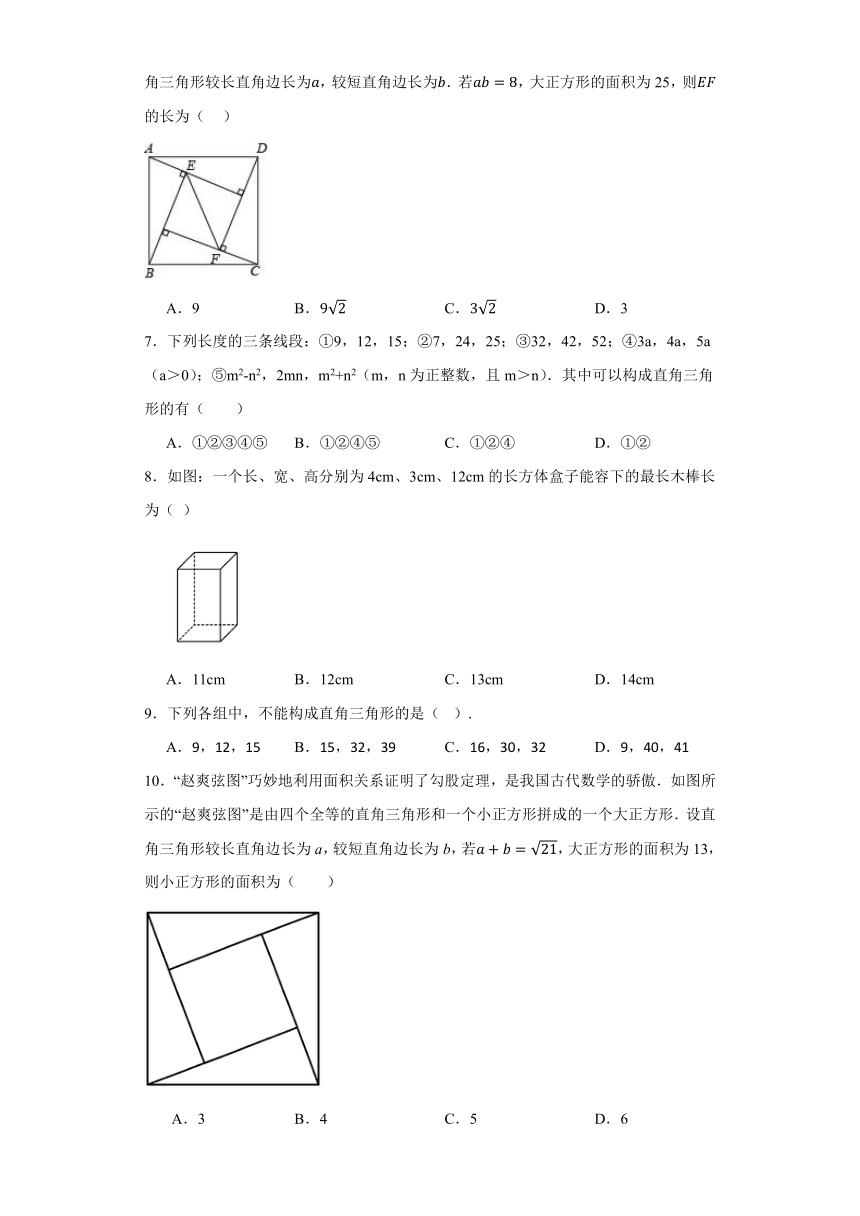
6.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为.若,大正方形的面积为25,则的长为( )
A.9 B. C. D.3
7.下列长度的三条线段:①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0);⑤m2-n2,2mn,m2+n2(m,n为正整数,且m>n).其中可以构成直角三角形的有( )
A.①②③④⑤ B.①②④⑤ C.①②④ D.①②
8.如图:一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为( )
A.11cm B.12cm C.13cm D.14cm
9.下列各组中,不能构成直角三角形的是( ).
A.9,12,15 B.15,32,39 C.16,30,32 D.9,40,41
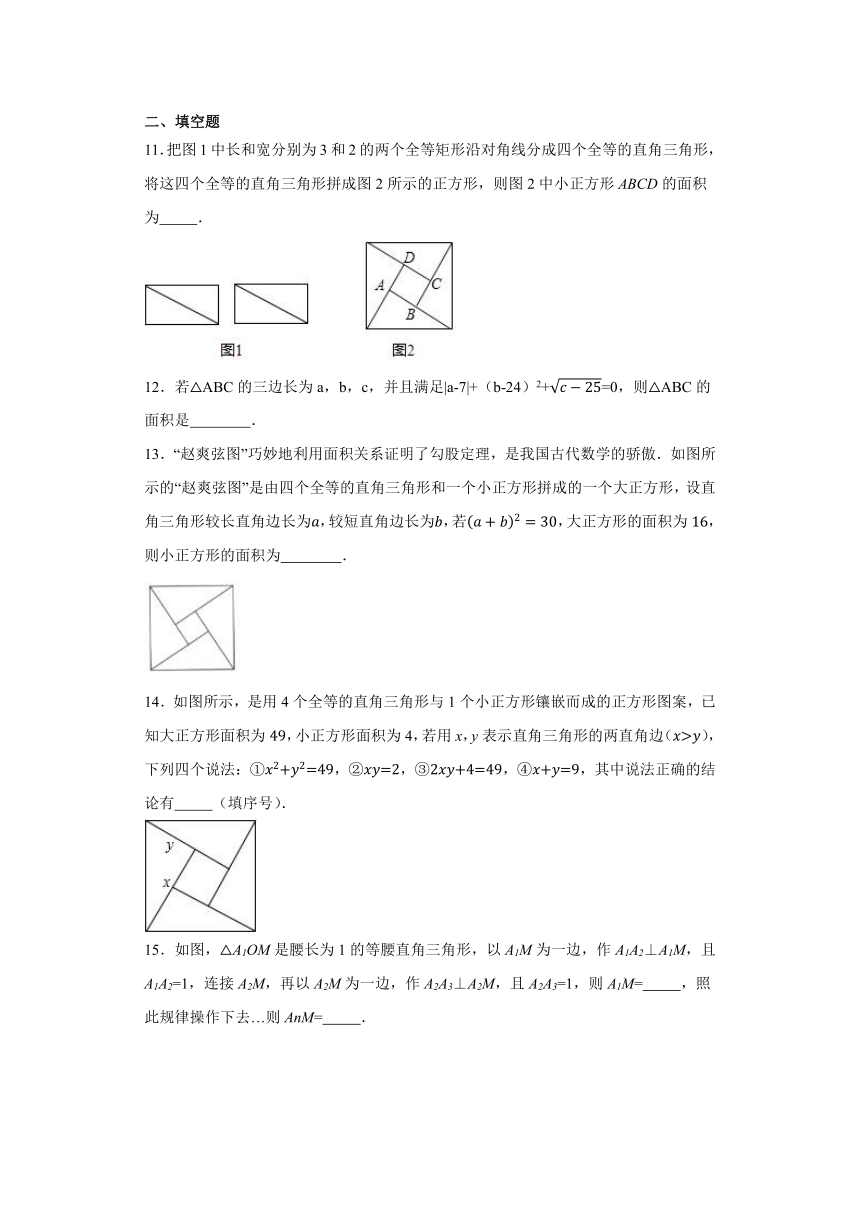
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
二、填空题
11.把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2所示的正方形,则图2中小正方形ABCD的面积为 .
12.若△ABC的三边长为a,b,c,并且满足|a-7|+(b-24)2+=0,则△ABC的面积是 .
13.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的面积为 .
14.如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为,小正方形面积为4,若用x,y表示直角三角形的两直角边(),下列四个说法:①,②,③,④,其中说法正确的结论有 (填序号).
15.如图,△A1OM是腰长为1的等腰直角三角形,以A1M为一边,作A1A2⊥A1M,且A1A2=1,连接A2M,再以A2M为一边,作A2A3⊥A2M,且A2A3=1,则A1M= ,照此规律操作下去…则AnM= .
三、解答题
16.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图中以格点为顶点画一个面积为10的正方形.
(2)把所作正方形分割成赵爽弦图.
17.《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?
18.(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
19.在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:
如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,求池水的深度.
20.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整:
∵S1= ,S2= ,S3= ,
∴S1+S2 S3.
即( )2+( )2=( )2.
21.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点E在上,,一滑板爱好者从A点滑到E点,则他滑行的最短距离为多少米?(边缘部分的厚度忽略不计)
一、单选题
1.《九章算术》中有一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?”题意是:有一个水池,水面是一个边长为10尺的正方形,在水池的正中央有一根芦苇,高出水面部分为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的(如图),则水深和芦苇长各多少尺?若设这根芦苇的长度为x尺,根据题意,所列方程正确的是( )
A. B.
C. D.
2.下列各组长度的线段中,可以组成直角三角形的是( )
A.1,2,3 B.3,4,5 C.1,,3 D.5,6,7
3.下列各组数中,是勾股数的是( )
A.7,8,9 B.6,8,11 C.5,12,14 D.3,4,5
4.下列四组线段中,能组成直角三角形的是( )
A.a=2,b=4,c=6 B.a=4,b=6,c=8
C.a=4,b=8,c=10 D.a=6,b=8,c=10
5.如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为,大正方形边长为,则一个直角三角形的面积等于( )
A. B. C. D.
6.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为.若,大正方形的面积为25,则的长为( )
A.9 B. C. D.3
7.下列长度的三条线段:①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0);⑤m2-n2,2mn,m2+n2(m,n为正整数,且m>n).其中可以构成直角三角形的有( )
A.①②③④⑤ B.①②④⑤ C.①②④ D.①②
8.如图:一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为( )
A.11cm B.12cm C.13cm D.14cm
9.下列各组中,不能构成直角三角形的是( ).
A.9,12,15 B.15,32,39 C.16,30,32 D.9,40,41
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
二、填空题
11.把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2所示的正方形,则图2中小正方形ABCD的面积为 .
12.若△ABC的三边长为a,b,c,并且满足|a-7|+(b-24)2+=0,则△ABC的面积是 .
13.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的面积为 .
14.如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为,小正方形面积为4,若用x,y表示直角三角形的两直角边(),下列四个说法:①,②,③,④,其中说法正确的结论有 (填序号).
15.如图,△A1OM是腰长为1的等腰直角三角形,以A1M为一边,作A1A2⊥A1M,且A1A2=1,连接A2M,再以A2M为一边,作A2A3⊥A2M,且A2A3=1,则A1M= ,照此规律操作下去…则AnM= .
三、解答题
16.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图中以格点为顶点画一个面积为10的正方形.
(2)把所作正方形分割成赵爽弦图.
17.《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?
18.(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
19.在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:
如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,求池水的深度.
20.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整:
∵S1= ,S2= ,S3= ,
∴S1+S2 S3.
即( )2+( )2=( )2.
21.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点E在上,,一滑板爱好者从A点滑到E点,则他滑行的最短距离为多少米?(边缘部分的厚度忽略不计)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
