人教版数学八年级上册 11.2与三角形有关的角第2课时三角形的外角 课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.2与三角形有关的角第2课时三角形的外角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 21:49:43 | ||
图片预览




文档简介
(共20张PPT)
11.2 与三角形有关的角
第2课时 三角形的外角
学习目标
1.理解三角形外角的概念, 能识别图形中的外角.
2.掌握三角形外角的性质, 熟练运用性质解决问题.
3.培养学生的推理能力.
复习回顾
1.在△ABC中,
(1)∠C=90°,∠A=30 °,则∠B= ;
(2)∠A=50 °,∠B=∠C, 则∠B= .
2.在△ABC中,
∠A:∠B:∠C=2:3:5,则∠A= ,
∠B= ,∠C= .
60°
65°
36°
54°
90°
A
C
B
1
D
A
C
B
1
D
新课引入
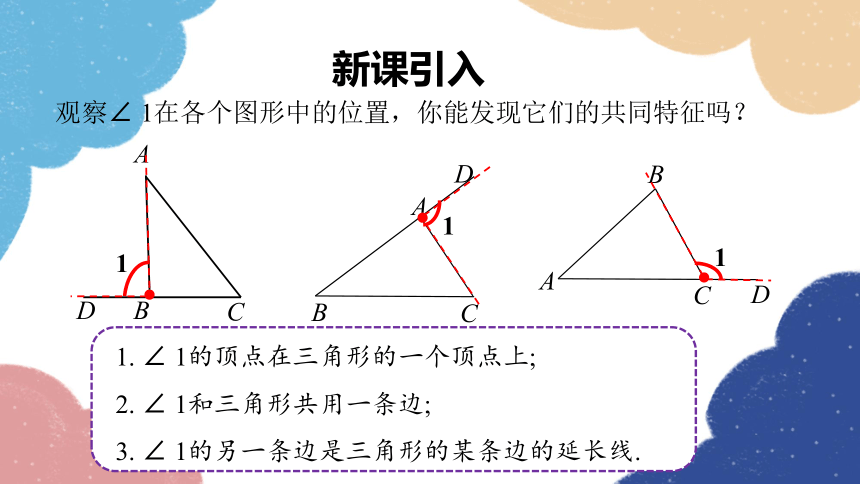
观察∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1和三角形共用一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.
新课引入
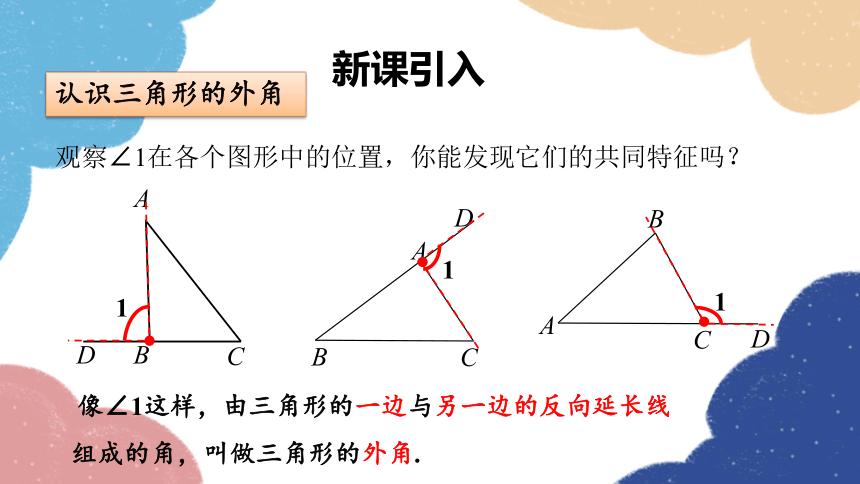
观察∠1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
像∠1这样,由三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
认识三角形的外角
三角形的外角
知识讲解
A
C
B
D
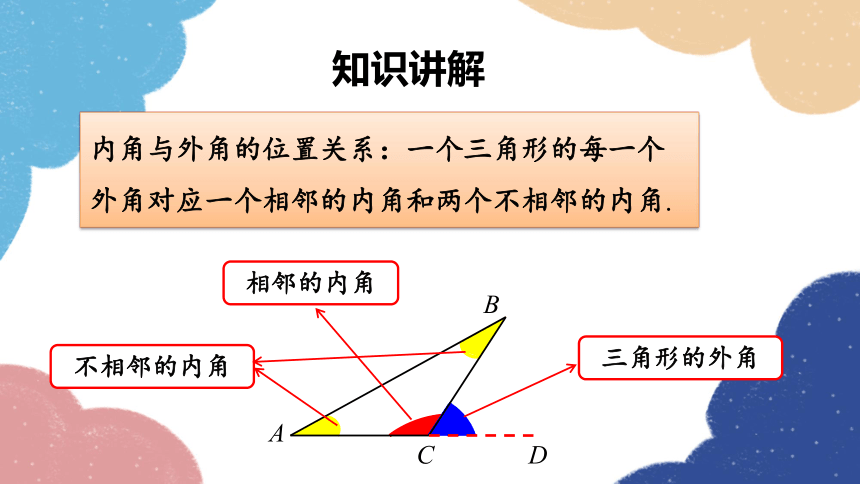
内角与外角的位置关系:一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
不相邻的内角
相邻的内角
A
B
D
E
F
C
A
B
D
E
F
C
知识讲解
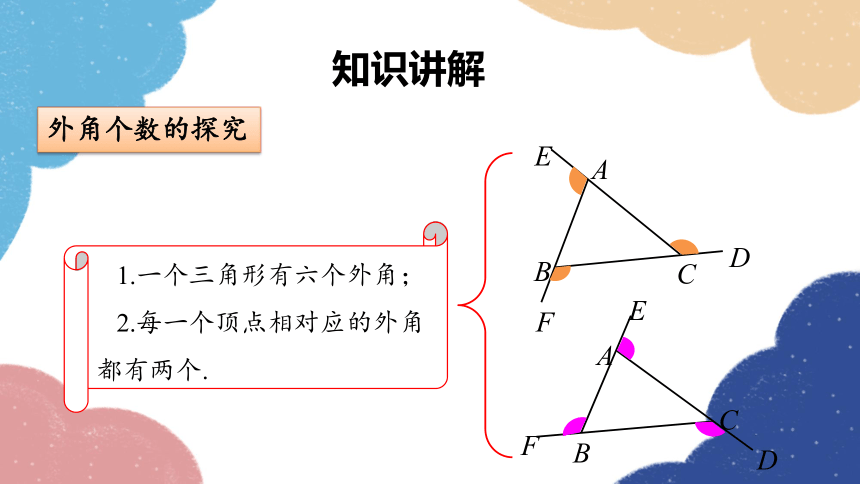
外角个数的探究
1.一个三角形有六个外角;
2.每一个顶点相对应的外角都有两个.
知识讲解
外角与内角大小关系的探究
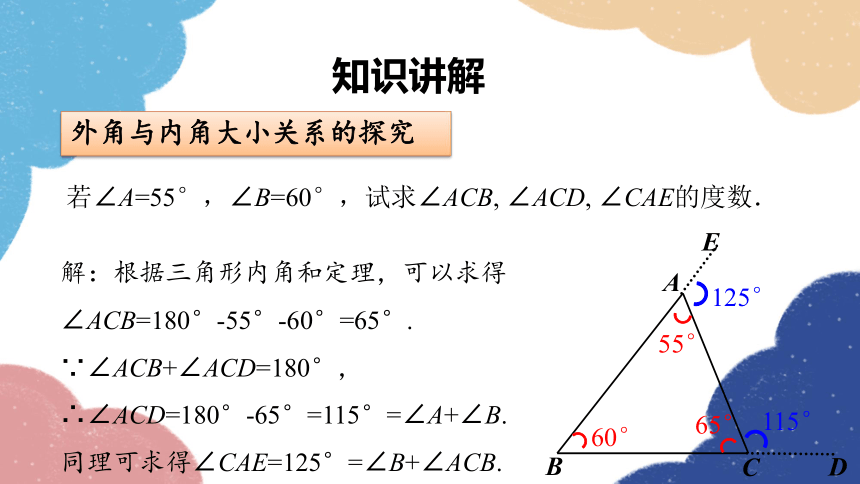
若∠A=55°,∠B=60°,试求∠ACB, ∠ACD, ∠CAE的度数.
A
B
C
D
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
解:根据三角形内角和定理,可以求得∠ACB=180°-55°-60°=65°.
∵∠ACB+∠ACD=180°,∴∠ACD=180°-65°=115°=∠A+∠B.
同理可求得∠CAE=125°=∠B+∠ACB.
E
知识讲解
外角与内角大小关系的探究
若∠A=55°,∠B=60°,试求∠ACB, ∠ACD, ∠CAE的度数.
∠ACD=∠A+∠B.
∠CAE=∠B+∠ACB.
三角形的外角等于与它
不相邻的两个内角的和.
是否适用于所有三角形?
A
B
C
D
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
E
外角与内角大小关系的探究
知识讲解
求证:∠ACD=∠B+∠A
A
B
C
D
证明:过C作CE平行于AB,
∴∠1=∠B (两直线平行同位角相等),
∠2=∠A (两直线平行内错角相等),
∴∠ACD=∠1+ ∠2=∠A+∠B
E
1
2
不借助辅助线,应该怎么证明?
三角形的一个外角等于与它不相邻的两个内角的和
外角与内角大小关系的探究
知识讲解
求证:∠ACD=∠B+∠A
A
B
C
D
证明:∵∠ACD+∠ACB=180°(邻补角的定义),
又∵∠A+ ∠B+ ∠ACB=180°(三角形内角和定理),
所以, ∠A+ ∠B= ∠ACD (等量代换).
∴∠ACD =180 ° -∠ACB
∴∠A+ ∠B =180 ° -∠ACB
外角与内角大小关系的探究
知识讲解
A
B
C
D
若∠ACD=∠B+∠A,
则∠ACD ∠A (<、>);
∠ACD ∠B (<、>).
>
>
三角形的一个外角大于任何一个与它不相邻的内角
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解:解法1:
∵ ∠4 =∠2 +∠3,
∠5 =∠1 +∠3,
∠6 =∠1 +∠2,
∴∠4 +∠5 +∠6
=(∠2+∠3)+(∠1+∠3)+(∠1+∠2)
= 2(∠1+∠2+∠3) = 2×180°=360°.
(三角形的一个外角等于与它不相邻的两个内角的和)
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解法2:
∵∠4+∠1=180°,
∠5+∠2=180°,
∠6+∠3=180°,
∴∠4 +∠5 +∠6 + ∠1+∠2 +∠3 = 540°.
∵∠1 + ∠2 + ∠3 =180°.
∴∠4 + ∠5 + ∠6= 540°-180°=360°.
(三角形的一个外角与它相邻的内角互补)
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解法3:
过A作AD∥BC,
∴ ∠5=∠7,
∠6=∠8.
∴ ∠4+∠5+∠6
=∠4+∠7+∠8=360°
(两直线平行,同位角相等)
8
D
7
总结归纳
性质一:三角形的一个外角等于与它不相邻的两个内角的和.
三角形外角的性质
性质二:三角形的一个外角大于任何一个与它不相邻的内角.
性质三:三角形的外角和=360°.
典例导学
例2 如图,BC⊥ED于O,∠A=27°,∠D=20°, 求∠B和∠ACB 的度数.
分析:B是△ABC的内角,在△ABC中,∠B与∠ACB都是所要求的,而∠ACB又是△COD的外角,根据“三角形的一个外角等于和它不相邻的两个内角的和”可求∠ACB,从而根据三角形的内角和定理可求∠B.
典例导学
例2 如图,BC⊥ED于O,∠A=27°,∠D=20°, 求∠B和∠ACB 的度数.
解:∵BC⊥ED,∴∠DOC=90°.
又∵∠ACB是△COD的外角,
∴∠ACB=∠COD+∠D=90°+20°=110°.
∴在△ABC中,∠B=180°-∠A-∠ACB=180°-27°-110°=43°.
典例导学
例3 如图,在△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是 .
【解析】比较角的大小关系,首先想到三角形的一个外角大于任何一个与它不相邻的内角.从上面的图形中可以看出:
∠1是△ABC的一个外角,所以它大于与它不相邻的内角∠2;
同理,∠2作为△AEF的一个外角,也大于与它不相邻的内角∠3.
∠1>∠2>∠3
随堂训练
如图,已知∠AEC=110°,求∠A+∠B+∠C+∠D的度数.
解:∵∠AEC是△ABE的外角,
∴∠AEC=∠A+∠B=110°.
∴∠AEC=∠C+∠D=110°.
∴∠A+∠B+∠C+∠D=220°.
∵∠AEC是△CDE的外角,
A
B
C
D
E
11.2 与三角形有关的角
第2课时 三角形的外角
学习目标
1.理解三角形外角的概念, 能识别图形中的外角.
2.掌握三角形外角的性质, 熟练运用性质解决问题.
3.培养学生的推理能力.
复习回顾
1.在△ABC中,
(1)∠C=90°,∠A=30 °,则∠B= ;
(2)∠A=50 °,∠B=∠C, 则∠B= .
2.在△ABC中,
∠A:∠B:∠C=2:3:5,则∠A= ,
∠B= ,∠C= .
60°
65°
36°
54°
90°
A
C
B
1
D
A
C
B
1
D
新课引入
观察∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1和三角形共用一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.
新课引入
观察∠1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
像∠1这样,由三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
认识三角形的外角
三角形的外角
知识讲解
A
C
B
D
内角与外角的位置关系:一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
不相邻的内角
相邻的内角
A
B
D
E
F
C
A
B
D
E
F
C
知识讲解
外角个数的探究
1.一个三角形有六个外角;
2.每一个顶点相对应的外角都有两个.
知识讲解
外角与内角大小关系的探究
若∠A=55°,∠B=60°,试求∠ACB, ∠ACD, ∠CAE的度数.
A
B
C
D
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
解:根据三角形内角和定理,可以求得∠ACB=180°-55°-60°=65°.
∵∠ACB+∠ACD=180°,∴∠ACD=180°-65°=115°=∠A+∠B.
同理可求得∠CAE=125°=∠B+∠ACB.
E
知识讲解
外角与内角大小关系的探究
若∠A=55°,∠B=60°,试求∠ACB, ∠ACD, ∠CAE的度数.
∠ACD=∠A+∠B.
∠CAE=∠B+∠ACB.
三角形的外角等于与它
不相邻的两个内角的和.
是否适用于所有三角形?
A
B
C
D
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
E
外角与内角大小关系的探究
知识讲解
求证:∠ACD=∠B+∠A
A
B
C
D
证明:过C作CE平行于AB,
∴∠1=∠B (两直线平行同位角相等),
∠2=∠A (两直线平行内错角相等),
∴∠ACD=∠1+ ∠2=∠A+∠B
E
1
2
不借助辅助线,应该怎么证明?
三角形的一个外角等于与它不相邻的两个内角的和
外角与内角大小关系的探究
知识讲解
求证:∠ACD=∠B+∠A
A
B
C
D
证明:∵∠ACD+∠ACB=180°(邻补角的定义),
又∵∠A+ ∠B+ ∠ACB=180°(三角形内角和定理),
所以, ∠A+ ∠B= ∠ACD (等量代换).
∴∠ACD =180 ° -∠ACB
∴∠A+ ∠B =180 ° -∠ACB
外角与内角大小关系的探究
知识讲解
A
B
C
D
若∠ACD=∠B+∠A,
则∠ACD ∠A (<、>);
∠ACD ∠B (<、>).
>
>
三角形的一个外角大于任何一个与它不相邻的内角
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解:解法1:
∵ ∠4 =∠2 +∠3,
∠5 =∠1 +∠3,
∠6 =∠1 +∠2,
∴∠4 +∠5 +∠6
=(∠2+∠3)+(∠1+∠3)+(∠1+∠2)
= 2(∠1+∠2+∠3) = 2×180°=360°.
(三角形的一个外角等于与它不相邻的两个内角的和)
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解法2:
∵∠4+∠1=180°,
∠5+∠2=180°,
∠6+∠3=180°,
∴∠4 +∠5 +∠6 + ∠1+∠2 +∠3 = 540°.
∵∠1 + ∠2 + ∠3 =180°.
∴∠4 + ∠5 + ∠6= 540°-180°=360°.
(三角形的一个外角与它相邻的内角互补)
例1 如图,∠4,∠5,∠6是△ABC 的三个外角,它们的和是多少?
典例导学
6
5
4
3
2
C
A
B
1
解法3:
过A作AD∥BC,
∴ ∠5=∠7,
∠6=∠8.
∴ ∠4+∠5+∠6
=∠4+∠7+∠8=360°
(两直线平行,同位角相等)
8
D
7
总结归纳
性质一:三角形的一个外角等于与它不相邻的两个内角的和.
三角形外角的性质
性质二:三角形的一个外角大于任何一个与它不相邻的内角.
性质三:三角形的外角和=360°.
典例导学
例2 如图,BC⊥ED于O,∠A=27°,∠D=20°, 求∠B和∠ACB 的度数.
分析:B是△ABC的内角,在△ABC中,∠B与∠ACB都是所要求的,而∠ACB又是△COD的外角,根据“三角形的一个外角等于和它不相邻的两个内角的和”可求∠ACB,从而根据三角形的内角和定理可求∠B.
典例导学
例2 如图,BC⊥ED于O,∠A=27°,∠D=20°, 求∠B和∠ACB 的度数.
解:∵BC⊥ED,∴∠DOC=90°.
又∵∠ACB是△COD的外角,
∴∠ACB=∠COD+∠D=90°+20°=110°.
∴在△ABC中,∠B=180°-∠A-∠ACB=180°-27°-110°=43°.
典例导学
例3 如图,在△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是 .
【解析】比较角的大小关系,首先想到三角形的一个外角大于任何一个与它不相邻的内角.从上面的图形中可以看出:
∠1是△ABC的一个外角,所以它大于与它不相邻的内角∠2;
同理,∠2作为△AEF的一个外角,也大于与它不相邻的内角∠3.
∠1>∠2>∠3
随堂训练
如图,已知∠AEC=110°,求∠A+∠B+∠C+∠D的度数.
解:∵∠AEC是△ABE的外角,
∴∠AEC=∠A+∠B=110°.
∴∠AEC=∠C+∠D=110°.
∴∠A+∠B+∠C+∠D=220°.
∵∠AEC是△CDE的外角,
A
B
C
D
E
