四川省成都东部新区养马高级中学2023-2024学年高二上学期开学考试数学试题(PDF版无答案)
文档属性
| 名称 | 四川省成都东部新区养马高级中学2023-2024学年高二上学期开学考试数学试题(PDF版无答案) |

|
|
| 格式 | |||
| 文件大小 | 736.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览

文档简介
东部新区养马高级中学 2022 级数学开学考试 2023.9
一、选择题(本题共 8道小题,每小题 5分,共 40分)
1
1.若 = , 则 2 =( )
3
2 7 4 2 7
A. B. C. √± D. ±
3 9 9 9
2.已知向量 = (1,1), = ( 2,3),那么| 2 | =( )
A. 5 B. 5√2 C. 8 D. √74
1 2
3.复数 = (i是虚数单位)在复平面内对应的点在( )
1+
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.已知 , 是两条不重合的直线, , , 是三个不重合的平面,则下列命题正确的是( )
A. 若 ∥ , ∥ ,则 ∥ B. 若 ⊥ , ⊥ ,则 ∥
C. 若 ⊥ , ⊥ ,则 ∥ D. 若 ∥ , ⊥ ,则 ⊥
5.在四边形 中, ∥ ,∠ = 120°, = 4, = 2, = 3, , 分别为 ,
的中点,则 =( )
9 5 7
A. B.﹣3 C. D.
2 2 2
+
6.在△ 中, = ,则△ 是( )
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
7.已知空间四边形 中, , 分别是 , 的中点,若 = 2, = 4, ⊥ ,则
与 所成的角为( )
A. 30° B. 45° C. 60° D. 90°
8.在三棱锥 中,SA ⊥ 平面 ABC,∠ABC = 90°,且 = 3, = 4, = 5,若球 在
三棱锥 的内部且与四个面都相切(称球 为三棱锥 的内切球),则球 的
表面积为()
16 4 32 16
A. B. C. D.
9 9 27 81
1
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
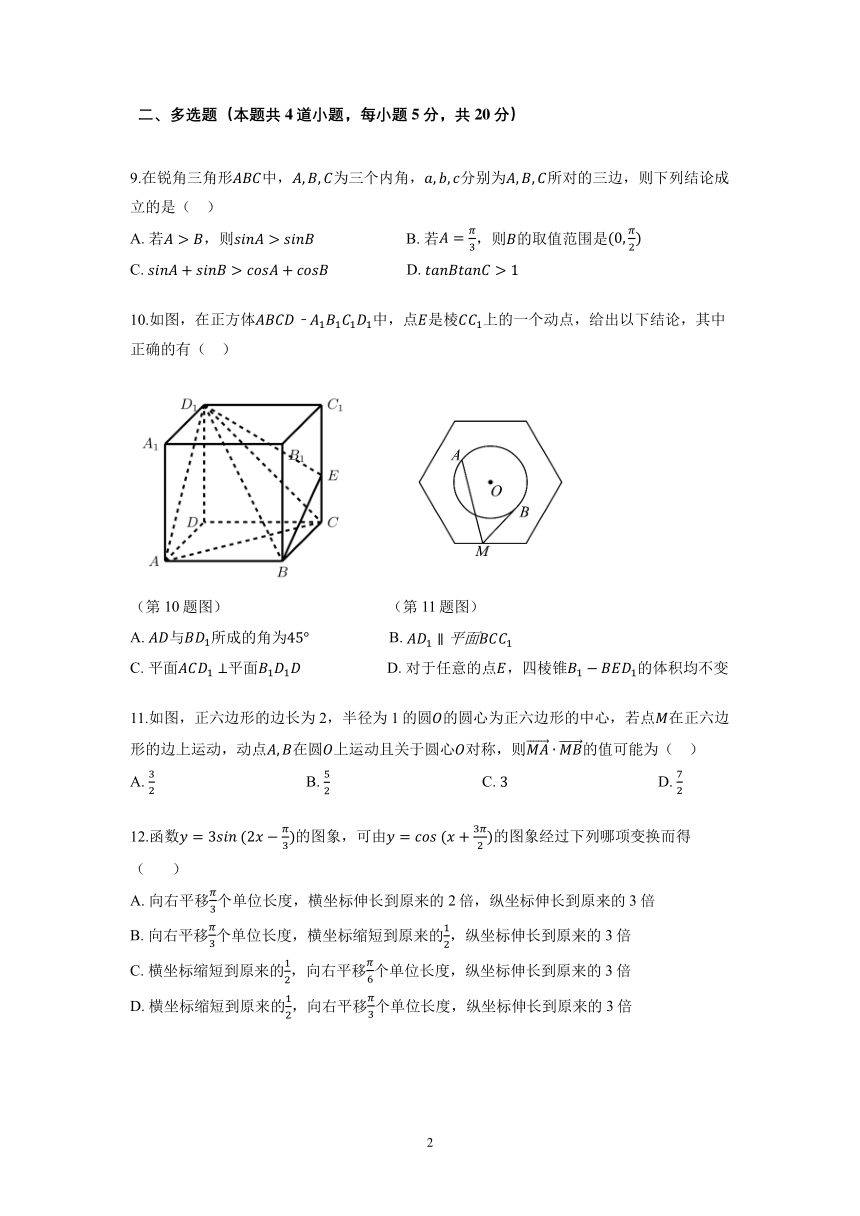
二、多选题(本题共 4道小题,每小题 5分,共 20分)
9.在锐角三角形 中, , , 为三个内角, , , 分别为 , , 所对的三边,则下列结论成
立的是( )
A. 若 > ,则 > B. 若 = ,则 的取值范围是(0, )
3 2
C. + > + D. > 1
10.如图,在正方体 ﹣ 1 1 1 1中,点 是棱 1上的一个动点,给出以下结论,其中
正确的有( )
(第 10 题图) (第 11 题图)
A. 与 1所成的角为45° B. 1 ∥ 平面 1
C. 平面 1 ⊥平面 1 1 D. 对于任意的点 ,四棱锥 1 1的体积均不变
11.如图,正六边形的边长为 2,半径为 1 的圆 的圆心为正六边形的中心,若点 在正六边
形的边上运动,动点 , 在圆 上运动且关于圆心 对称,则 的值可能为( )
3 5 7
A. B. C. 3 D.
2 2 2
3
12.函数 = 3 (2 )的图象,可由 = ( + )的图象经过下列哪项变换而得
3 2
( )
A. 向右平移 个单位长度,横坐标伸长到原来的 2 倍,纵坐标伸长到原来的 3 倍
3
1
B. 向右平移 个单位长度,横坐标缩短到原来的 ,纵坐标伸长到原来的 3 倍
3 2
1
C. 横坐标缩短到原来的 ,向右平移 个单位长度,纵坐标伸长到原来的 3 倍
2 6
1
D. 横坐标缩短到原来的 ,向右平移 个单位长度,纵坐标伸长到原来的 3 倍
2 3
2
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
三、填空题(本题共 4道小题,每小题 5分,共 20分)
13. 在平行四边形 中, + + =_________.
14. 74° 14°﹣ 74° 14°的值为 ___________.
15. 设 m为实数,复数 m(3+i)﹣(2+i)在复平面内所对应的点位于第四象限,则 m的取值
范围为__________.
16. 已知三棱锥P ABC的四个顶点在球 的表面上, ⊥平面 , = 6, =
2√3, = 2, = 4,则球 的表面积为______;若 是 的中点,过 作球的截面,则截
面面积的最小值是_______.
四、解答题(本题共 6道小题,第 1题 10分,第 2题 12分,第 3题 12分,第 4题 12分,
第 5题 12分,第 6题 12分,共 70分)
17. 已知向量 = (2 + , 1), = (2, 2), = (3 , 1), = (1, )( ∈ , ∈ )
(1)若 ∈ [0,2 ),且 ∥ ( ),求 的值;
(2)是否存在实数 ,使得( + ) ⊥ ( )?若存在,求出 的取值范围;若不存在,请
说明理由.
18. 如图,在棱长为 6 的正方体 ﹣ 1 1 1 1中,点 是 1 的中点, 与 交于点 .
(1)求证: 1 ∥ 平面 ;
(2)求三棱锥 的体积.
3
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
19. 已知向量 = ( , ), = ( , √3 ),函数 ( ) = 2 √3.
(1)求 ( )的最小正周期T;
(2)当0 ≤ ≤ 时,求 ( )的零点和单调递增区间.
20. 四棱锥 的底面是边长为 1 的菱形,∠ = 60°, 是 的中点, =
√3, ⊥平面 .
(1)求直线 与平面 所成角;
(2)求证: 平面 ⊥平面 .
21. 如图,我国南海某处的一个圆形海域上有四个小岛,小岛 B与小岛 A、小岛 C相距都为
3
5km,与小岛 D相距为3√5km.∠ 为钝角,且 = .
5
(1)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(2)记∠ 为 ,∠ 为 ,求 (2 + )的值.
22.已知向量 = (2√3, ), = ( 2 , 2 ),函数 ( ) = √3 ( > 0),
( )相邻对称轴之间的距离为 .
2
(1)求 ( )的单调递减区间;
1
(2)将函数 ( )图象上所有点的横坐标缩短为原来的 ,再向左平移 个单位得 ( )的图
2 12
象,若关于 x的方程 ( ) = 在[ , ]上只有一个解,求实数 m的取值范围.
12 6
4
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
一、选择题(本题共 8道小题,每小题 5分,共 40分)
1
1.若 = , 则 2 =( )
3
2 7 4 2 7
A. B. C. √± D. ±
3 9 9 9
2.已知向量 = (1,1), = ( 2,3),那么| 2 | =( )
A. 5 B. 5√2 C. 8 D. √74
1 2
3.复数 = (i是虚数单位)在复平面内对应的点在( )
1+
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.已知 , 是两条不重合的直线, , , 是三个不重合的平面,则下列命题正确的是( )
A. 若 ∥ , ∥ ,则 ∥ B. 若 ⊥ , ⊥ ,则 ∥
C. 若 ⊥ , ⊥ ,则 ∥ D. 若 ∥ , ⊥ ,则 ⊥
5.在四边形 中, ∥ ,∠ = 120°, = 4, = 2, = 3, , 分别为 ,
的中点,则 =( )
9 5 7
A. B.﹣3 C. D.
2 2 2
+
6.在△ 中, = ,则△ 是( )
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
7.已知空间四边形 中, , 分别是 , 的中点,若 = 2, = 4, ⊥ ,则
与 所成的角为( )
A. 30° B. 45° C. 60° D. 90°
8.在三棱锥 中,SA ⊥ 平面 ABC,∠ABC = 90°,且 = 3, = 4, = 5,若球 在
三棱锥 的内部且与四个面都相切(称球 为三棱锥 的内切球),则球 的
表面积为()
16 4 32 16
A. B. C. D.
9 9 27 81
1
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
二、多选题(本题共 4道小题,每小题 5分,共 20分)
9.在锐角三角形 中, , , 为三个内角, , , 分别为 , , 所对的三边,则下列结论成
立的是( )
A. 若 > ,则 > B. 若 = ,则 的取值范围是(0, )
3 2
C. + > + D. > 1
10.如图,在正方体 ﹣ 1 1 1 1中,点 是棱 1上的一个动点,给出以下结论,其中
正确的有( )
(第 10 题图) (第 11 题图)
A. 与 1所成的角为45° B. 1 ∥ 平面 1
C. 平面 1 ⊥平面 1 1 D. 对于任意的点 ,四棱锥 1 1的体积均不变
11.如图,正六边形的边长为 2,半径为 1 的圆 的圆心为正六边形的中心,若点 在正六边
形的边上运动,动点 , 在圆 上运动且关于圆心 对称,则 的值可能为( )
3 5 7
A. B. C. 3 D.
2 2 2
3
12.函数 = 3 (2 )的图象,可由 = ( + )的图象经过下列哪项变换而得
3 2
( )
A. 向右平移 个单位长度,横坐标伸长到原来的 2 倍,纵坐标伸长到原来的 3 倍
3
1
B. 向右平移 个单位长度,横坐标缩短到原来的 ,纵坐标伸长到原来的 3 倍
3 2
1
C. 横坐标缩短到原来的 ,向右平移 个单位长度,纵坐标伸长到原来的 3 倍
2 6
1
D. 横坐标缩短到原来的 ,向右平移 个单位长度,纵坐标伸长到原来的 3 倍
2 3
2
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
三、填空题(本题共 4道小题,每小题 5分,共 20分)
13. 在平行四边形 中, + + =_________.
14. 74° 14°﹣ 74° 14°的值为 ___________.
15. 设 m为实数,复数 m(3+i)﹣(2+i)在复平面内所对应的点位于第四象限,则 m的取值
范围为__________.
16. 已知三棱锥P ABC的四个顶点在球 的表面上, ⊥平面 , = 6, =
2√3, = 2, = 4,则球 的表面积为______;若 是 的中点,过 作球的截面,则截
面面积的最小值是_______.
四、解答题(本题共 6道小题,第 1题 10分,第 2题 12分,第 3题 12分,第 4题 12分,
第 5题 12分,第 6题 12分,共 70分)
17. 已知向量 = (2 + , 1), = (2, 2), = (3 , 1), = (1, )( ∈ , ∈ )
(1)若 ∈ [0,2 ),且 ∥ ( ),求 的值;
(2)是否存在实数 ,使得( + ) ⊥ ( )?若存在,求出 的取值范围;若不存在,请
说明理由.
18. 如图,在棱长为 6 的正方体 ﹣ 1 1 1 1中,点 是 1 的中点, 与 交于点 .
(1)求证: 1 ∥ 平面 ;
(2)求三棱锥 的体积.
3
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
19. 已知向量 = ( , ), = ( , √3 ),函数 ( ) = 2 √3.
(1)求 ( )的最小正周期T;
(2)当0 ≤ ≤ 时,求 ( )的零点和单调递增区间.
20. 四棱锥 的底面是边长为 1 的菱形,∠ = 60°, 是 的中点, =
√3, ⊥平面 .
(1)求直线 与平面 所成角;
(2)求证: 平面 ⊥平面 .
21. 如图,我国南海某处的一个圆形海域上有四个小岛,小岛 B与小岛 A、小岛 C相距都为
3
5km,与小岛 D相距为3√5km.∠ 为钝角,且 = .
5
(1)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(2)记∠ 为 ,∠ 为 ,求 (2 + )的值.
22.已知向量 = (2√3, ), = ( 2 , 2 ),函数 ( ) = √3 ( > 0),
( )相邻对称轴之间的距离为 .
2
(1)求 ( )的单调递减区间;
1
(2)将函数 ( )图象上所有点的横坐标缩短为原来的 ,再向左平移 个单位得 ( )的图
2 12
象,若关于 x的方程 ( ) = 在[ , ]上只有一个解,求实数 m的取值范围.
12 6
4
{#{QQABBYYUogigABAAABgCQQWCCAIQkBCCACgORBAAIAABiRNABAA=}#}
同课章节目录
