黑龙江省大庆市肇源县向阳学校等三校联考2023-2024学年八年级上学期开学考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省大庆市肇源县向阳学校等三校联考2023-2024学年八年级上学期开学考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览



文档简介
初三数学学科试题
考生注意:
1.答题前,考生先将自己的姓名、班级、考号填写清楚,将准考证号填写在相应区域并填涂。
2.答题时用黑色字迹的钢笔或签字笔在答题卡相应位置作答,在试题卷上作答无效。
3.考试时间120分钟。全卷共三道大题,总分120分。
一、单选题(每题3分,共30分)
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对边平行且相等 B.对角线互相垂直
C.每条对角线平分一组对角. D.四边相等
2.下列方程,是一元二次方程(其中,是未知数)的个数是( )
①,②,③,④
A.1个 B.2个 C.3个 D.4个
3.已知压力、压强与受力面积之间有如下关系式:.当为定值时,下图中大致表示压强与受力面积之间函数关系的是( )
A. B.
C. D.
4.若反比例函数的图象在一、三象限,则的值可以是( )
A.1 B.2 C.3 D.4
5.一天晚上,小伟帮助妈妈清洗四个绿、白、蓝、红颜色不同的有盖茶杯,突然停电了,小伟随机将其中一个杯盖和一个茶杯搭配在一起.则这个茶杯颜色搭配恰好正确的概率为( )
A. B. C. D.
6.如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( )
① ② ③ ④ ⑤
A.①②③④⑤ B.②④①③⑤ C.⑤④①③② D.⑤③①④②
7.某商店将一批夏装降价处理,经过两次降价后,由每件100元降至81元,求平均每次降价的百分率.设平均每次降价的百分率为,可列方程( )
A. B.
C. D.
8.若点,,都在反比例函数的图象上,其中,则,,的大小关系是( )
A. B. C. D.
9.如图,为等腰的斜边上的一动点,连接,,,垂足分别为点、,已知,以下结论错误的是( )
A. B.若,则
C. D.若时,
10.如图,在平面直角坐标系中,正方形的顶点,分别在轴、轴上,反比例函数(,)的图象与正方形的两边,分别交于点,,轴,垂足为,连接,,,下列结论:①;②四边形与的面积相等;③;④若,,则点的坐标为.其中正确的是( )
A.①② B.①②④ C.②③④ D.①②③④
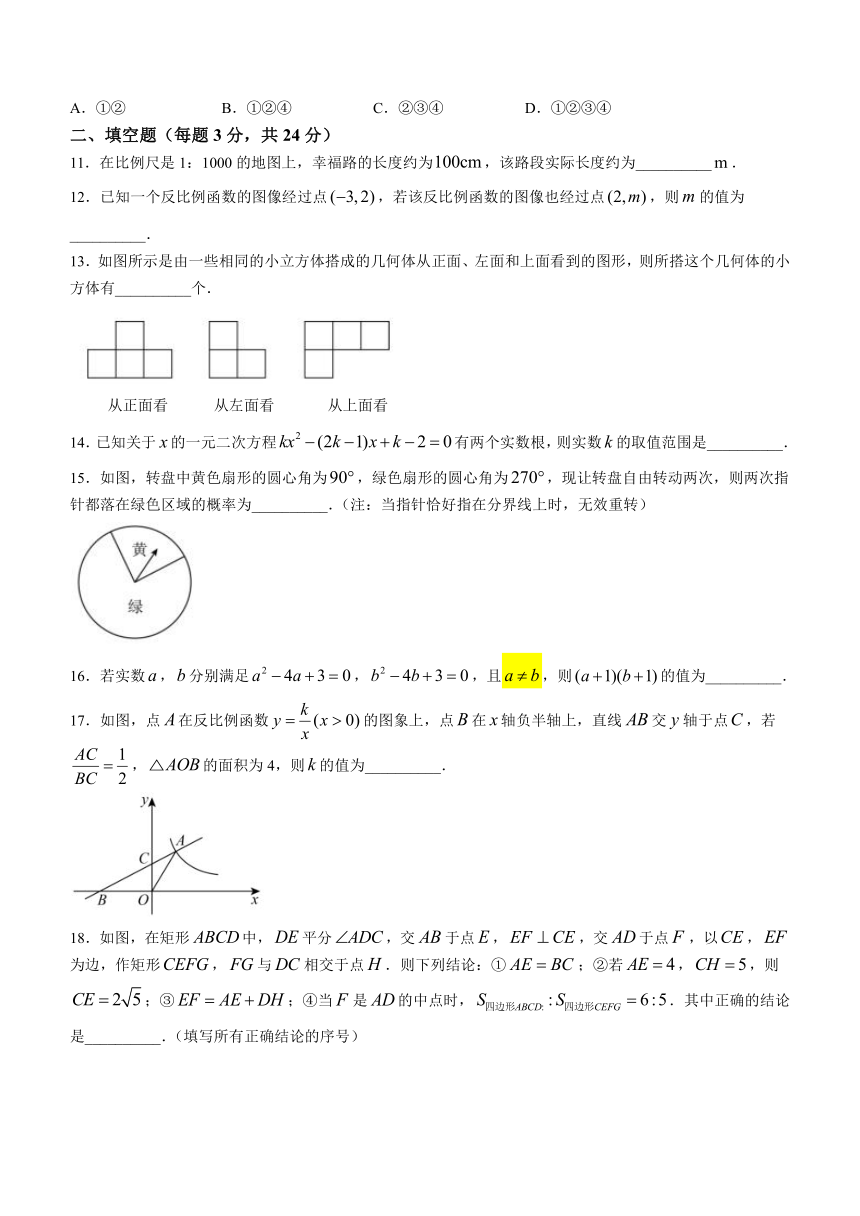
二、填空题(每题3分,共24分)
11.在比例尺是1:1000的地图上,幸福路的长度约为,该路段实际长度约为__________.
12.已知一个反比例函数的图像经过点,若该反比例函数的图像也经过点,则的值为__________.
13.如图所示是由一些相同的小立方体搭成的几何体从正面、左面和上面看到的图形,则所搭这个几何体的小方体有__________个.
从正面看 从左面看 从上面看
14.已知关于的一元二次方程有两个实数根,则实数的取值范围是__________.
15.如图,转盘中黄色扇形的圆心角为,绿色扇形的圆心角为,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为__________.(注:当指针恰好指在分界线上时,无效重转)
16.若实数,分别满足,,且,则的值为__________.
17.如图,点在反比例函数的图象上,点在轴负半轴上,直线交轴于点,若,的面积为4,则的值为__________.
18.如图,在矩形中,平分,交于点,,交于点,以,为边,作矩形,与相交于点.则下列结论:①;②若,,则;③;④当是的中点时,.其中正确的结论是__________.(填写所有正确结论的序号)
三、解答题
19.(9分)解下列一元二次方程:
(1)
(2)
(3)
20.(5分)在平面直角坐标系中的位置如图所示,网格中每个小正方形的边长都是1个单位长度.
(1)请画出关于轴对称的点,,的对应点分别为,,;
(2)请以原点为位似中心,在第四象限内画一个,使它与的相似比为2:1.
21.(5分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园(围墙最长可利用),现在已备足可以砌长的墙的材料.
(1)当长度是多少时,矩形花园的面积为150平方米;
(2)能否围成矩形花园面积为220平方米,为什么?
22.(5分)如图,在和中,,.
(1)求证:;
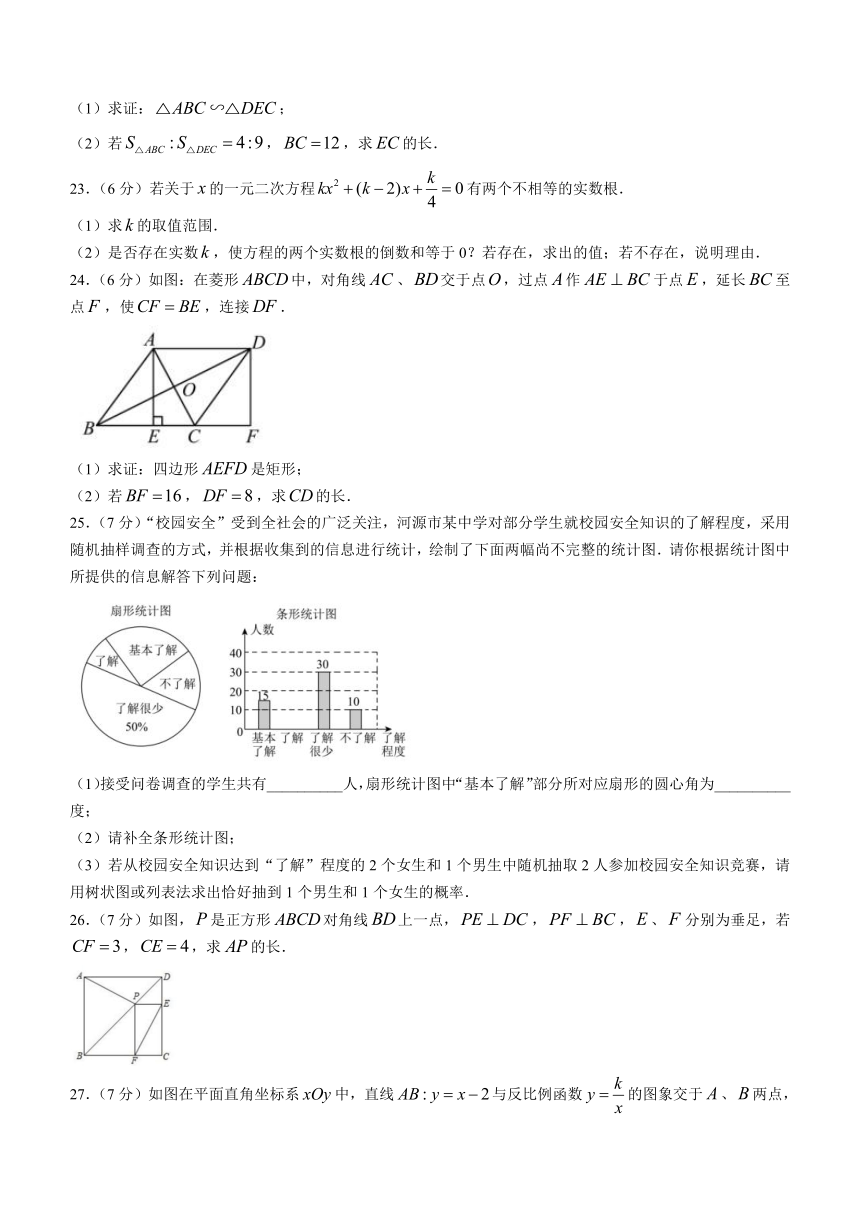
(2)若,,求的长.
23.(6分)若关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围.
(2)是否存在实数,使方程的两个实数根的倒数和等于0?若存在,求出的值;若不存在,说明理由.
24.(6分)如图:在菱形中,对角线、交于点,过点作于点,延长至点,使,连接.
(1)求证:四边形是矩形;
(2)若,,求的长.
25.(7分)“校园安全”受到全社会的广泛关注,河源市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有__________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为__________度;
(2)请补全条形统计图;
(3)若从校园安全知识达到“了解”程度的2个女生和1个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
26.(7分)如图,是正方形对角线上一点,,,、分别为垂足,若,,求的长.
27.(7分)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
28.(9分)如图,在矩形中,,,动点从点开始以每秒2个单位长度沿向终点运动,同时,动点从点开始沿以每秒3个单位长度向终点运动,它们同时到达终点.连接交于点.过点作,交直线于点.
备用图
(1)当点在线段上时,求证:.
(2)当时,求的面积.
(3)在,的运动过程中,是否存在某一位置,使得以点,,为顶点的三角形与相似?若存在,求的长;若不存在,请说明理由.
初三数学参考答案:
一、选择题
1.A 2.A 3.D 4.A 5.B 6.B 7.A 8.B 9.D 10.B
二、填空题
11.1000 12. 13.5 14.且
15. 16.8 17.4 18.①②④
三、简答题
19.(1), (2), (3),
20.【详解】(1)解:如图所示,
,图形关于轴对称的中,,
∴根据对称的性质可知,即为所求图形.
(2)解:如图所示,
,,,
∴连接,
∴,,,
∴,,,
且,,,
∴,,,符合题意,
∴即为所求图形.
21.【详解】(1)解:设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:当长度是时,矩形花园的面积为.
(2)不能,理由如下:
设,则,
依题意得:,
整理得:.
,
该方程无实数根,
不能围成面积为的矩形花园.
22.【详解】(1)∵,
∴,
∴,
∵,
∴.
(2)由(1)得,,
∵,
∴,
∵,
∴.
23.【详解】(1)∵一元二次方程有两个不相等的实数根
∴,
解得且
(2)假设存在实数k,使方程两实数根的倒数和为0
设方程的两根为.则
∴
即,且
解得
又∵
∴不存在实数k,使方程两实数根的倒数和为0
24.【详解】(1)在菱形中,,,
∵,
∴,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形;
(2)在菱形中,,
∵,
∴,
∵在矩形中,,
∵,
∴在中,,
解得:.
25.【详解】(1)∵了解很少的有30人,占50%
∴接受问卷调查的学生共有:(人)
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:.
故答案为:60,90.
(2)补充条形统计图如图所示
了解的人数有:(人)
(3)列表法如图所示
第一人 第二人 女1 女2 男
女1 (女1,女2) (女1,男)
女2 (女2,女1) (女2,男)
男 (男,女1) (男,女2)
则所有等可能性的结果有6种,其中恰好是一个男生一个女生的情况有4种,
所以
26.【详解】如图,连接PC,
四边形ABCD是正方形,
,,
,
≌,
,
四边形ABCD是正方形,
,
,,
四边形PFCE是矩形,
,
,
在中,,
,
.
27.【详解】(1)解:把点代入直线得:
∴点A的坐标为:,
∵反比例函数的图象过点A,
∴,
即反比例函数的解析式为,
(2)解:由(1)得:点A的坐标为:,
同理可求,点B的坐标为:,
∴不等式的解集为或;
(3)解:把代入得:,
即点C的坐标为:,
∴,
∵,
∴,
∴,
当点P的纵坐标为3时,则,解得,
当点P的纵坐标为时,则,解得,
∴点P的坐标为或.
28.【详解】(1)当点Q在线段上时,由题意可得:,,,
∴,
∴.
(2)①当点Q在上时,如图1,.过点E作的垂线交于点M,交于点N.
由,得.
由,得,
∴,
∴.
②当点Q在上时,如图2,作于点M,设.
,.
同理:,
∴,
∴.
同理:,得,
∴.
∴,解得,
∴.
∴的面积为或.
(3)①当点Q在上时,设,则.
若点F在Q的右侧,如图3,当,则.
作于点H,而,
∴,则,
∴.
∵,
∴,
解得.
∴.
若点F在Q的左侧,如图4,,点F与点C重合.
∵,
又∵
∴.
∵由结合对顶角可得:,而,
∴,
∴,即,则,
∴.
②当点Q在AD上时,如图5,,,,
作于点N,于点G.,则,
由,得,
∴,
∴.
同理可得:,
设,则,.
∴,,
由,得,,
∴,.
由题意,,
设,则,,,
由,得,即,
化简,得,
解得(舍去),.
∴.
综上所述,BP的长为或2或.
考生注意:
1.答题前,考生先将自己的姓名、班级、考号填写清楚,将准考证号填写在相应区域并填涂。
2.答题时用黑色字迹的钢笔或签字笔在答题卡相应位置作答,在试题卷上作答无效。
3.考试时间120分钟。全卷共三道大题,总分120分。
一、单选题(每题3分,共30分)
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对边平行且相等 B.对角线互相垂直
C.每条对角线平分一组对角. D.四边相等
2.下列方程,是一元二次方程(其中,是未知数)的个数是( )
①,②,③,④
A.1个 B.2个 C.3个 D.4个
3.已知压力、压强与受力面积之间有如下关系式:.当为定值时,下图中大致表示压强与受力面积之间函数关系的是( )
A. B.
C. D.
4.若反比例函数的图象在一、三象限,则的值可以是( )
A.1 B.2 C.3 D.4
5.一天晚上,小伟帮助妈妈清洗四个绿、白、蓝、红颜色不同的有盖茶杯,突然停电了,小伟随机将其中一个杯盖和一个茶杯搭配在一起.则这个茶杯颜色搭配恰好正确的概率为( )
A. B. C. D.
6.如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( )
① ② ③ ④ ⑤
A.①②③④⑤ B.②④①③⑤ C.⑤④①③② D.⑤③①④②
7.某商店将一批夏装降价处理,经过两次降价后,由每件100元降至81元,求平均每次降价的百分率.设平均每次降价的百分率为,可列方程( )
A. B.
C. D.
8.若点,,都在反比例函数的图象上,其中,则,,的大小关系是( )
A. B. C. D.
9.如图,为等腰的斜边上的一动点,连接,,,垂足分别为点、,已知,以下结论错误的是( )
A. B.若,则
C. D.若时,
10.如图,在平面直角坐标系中,正方形的顶点,分别在轴、轴上,反比例函数(,)的图象与正方形的两边,分别交于点,,轴,垂足为,连接,,,下列结论:①;②四边形与的面积相等;③;④若,,则点的坐标为.其中正确的是( )
A.①② B.①②④ C.②③④ D.①②③④
二、填空题(每题3分,共24分)
11.在比例尺是1:1000的地图上,幸福路的长度约为,该路段实际长度约为__________.
12.已知一个反比例函数的图像经过点,若该反比例函数的图像也经过点,则的值为__________.
13.如图所示是由一些相同的小立方体搭成的几何体从正面、左面和上面看到的图形,则所搭这个几何体的小方体有__________个.
从正面看 从左面看 从上面看
14.已知关于的一元二次方程有两个实数根,则实数的取值范围是__________.
15.如图,转盘中黄色扇形的圆心角为,绿色扇形的圆心角为,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为__________.(注:当指针恰好指在分界线上时,无效重转)
16.若实数,分别满足,,且,则的值为__________.
17.如图,点在反比例函数的图象上,点在轴负半轴上,直线交轴于点,若,的面积为4,则的值为__________.
18.如图,在矩形中,平分,交于点,,交于点,以,为边,作矩形,与相交于点.则下列结论:①;②若,,则;③;④当是的中点时,.其中正确的结论是__________.(填写所有正确结论的序号)
三、解答题
19.(9分)解下列一元二次方程:
(1)
(2)
(3)
20.(5分)在平面直角坐标系中的位置如图所示,网格中每个小正方形的边长都是1个单位长度.
(1)请画出关于轴对称的点,,的对应点分别为,,;
(2)请以原点为位似中心,在第四象限内画一个,使它与的相似比为2:1.
21.(5分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园(围墙最长可利用),现在已备足可以砌长的墙的材料.
(1)当长度是多少时,矩形花园的面积为150平方米;
(2)能否围成矩形花园面积为220平方米,为什么?
22.(5分)如图,在和中,,.
(1)求证:;
(2)若,,求的长.
23.(6分)若关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围.
(2)是否存在实数,使方程的两个实数根的倒数和等于0?若存在,求出的值;若不存在,说明理由.
24.(6分)如图:在菱形中,对角线、交于点,过点作于点,延长至点,使,连接.
(1)求证:四边形是矩形;
(2)若,,求的长.
25.(7分)“校园安全”受到全社会的广泛关注,河源市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有__________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为__________度;
(2)请补全条形统计图;
(3)若从校园安全知识达到“了解”程度的2个女生和1个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
26.(7分)如图,是正方形对角线上一点,,,、分别为垂足,若,,求的长.
27.(7分)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
28.(9分)如图,在矩形中,,,动点从点开始以每秒2个单位长度沿向终点运动,同时,动点从点开始沿以每秒3个单位长度向终点运动,它们同时到达终点.连接交于点.过点作,交直线于点.
备用图
(1)当点在线段上时,求证:.
(2)当时,求的面积.
(3)在,的运动过程中,是否存在某一位置,使得以点,,为顶点的三角形与相似?若存在,求的长;若不存在,请说明理由.
初三数学参考答案:
一、选择题
1.A 2.A 3.D 4.A 5.B 6.B 7.A 8.B 9.D 10.B
二、填空题
11.1000 12. 13.5 14.且
15. 16.8 17.4 18.①②④
三、简答题
19.(1), (2), (3),
20.【详解】(1)解:如图所示,
,图形关于轴对称的中,,
∴根据对称的性质可知,即为所求图形.
(2)解:如图所示,
,,,
∴连接,
∴,,,
∴,,,
且,,,
∴,,,符合题意,
∴即为所求图形.
21.【详解】(1)解:设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:当长度是时,矩形花园的面积为.
(2)不能,理由如下:
设,则,
依题意得:,
整理得:.
,
该方程无实数根,
不能围成面积为的矩形花园.
22.【详解】(1)∵,
∴,
∴,
∵,
∴.
(2)由(1)得,,
∵,
∴,
∵,
∴.
23.【详解】(1)∵一元二次方程有两个不相等的实数根
∴,
解得且
(2)假设存在实数k,使方程两实数根的倒数和为0
设方程的两根为.则
∴
即,且
解得
又∵
∴不存在实数k,使方程两实数根的倒数和为0
24.【详解】(1)在菱形中,,,
∵,
∴,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形;
(2)在菱形中,,
∵,
∴,
∵在矩形中,,
∵,
∴在中,,
解得:.
25.【详解】(1)∵了解很少的有30人,占50%
∴接受问卷调查的学生共有:(人)
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:.
故答案为:60,90.
(2)补充条形统计图如图所示
了解的人数有:(人)
(3)列表法如图所示
第一人 第二人 女1 女2 男
女1 (女1,女2) (女1,男)
女2 (女2,女1) (女2,男)
男 (男,女1) (男,女2)
则所有等可能性的结果有6种,其中恰好是一个男生一个女生的情况有4种,
所以
26.【详解】如图,连接PC,
四边形ABCD是正方形,
,,
,
≌,
,
四边形ABCD是正方形,
,
,,
四边形PFCE是矩形,
,
,
在中,,
,
.
27.【详解】(1)解:把点代入直线得:
∴点A的坐标为:,
∵反比例函数的图象过点A,
∴,
即反比例函数的解析式为,
(2)解:由(1)得:点A的坐标为:,
同理可求,点B的坐标为:,
∴不等式的解集为或;
(3)解:把代入得:,
即点C的坐标为:,
∴,
∵,
∴,
∴,
当点P的纵坐标为3时,则,解得,
当点P的纵坐标为时,则,解得,
∴点P的坐标为或.
28.【详解】(1)当点Q在线段上时,由题意可得:,,,
∴,
∴.
(2)①当点Q在上时,如图1,.过点E作的垂线交于点M,交于点N.
由,得.
由,得,
∴,
∴.
②当点Q在上时,如图2,作于点M,设.
,.
同理:,
∴,
∴.
同理:,得,
∴.
∴,解得,
∴.
∴的面积为或.
(3)①当点Q在上时,设,则.
若点F在Q的右侧,如图3,当,则.
作于点H,而,
∴,则,
∴.
∵,
∴,
解得.
∴.
若点F在Q的左侧,如图4,,点F与点C重合.
∵,
又∵
∴.
∵由结合对顶角可得:,而,
∴,
∴,即,则,
∴.
②当点Q在AD上时,如图5,,,,
作于点N,于点G.,则,
由,得,
∴,
∴.
同理可得:,
设,则,.
∴,,
由,得,,
∴,.
由题意,,
设,则,,,
由,得,即,
化简,得,
解得(舍去),.
∴.
综上所述,BP的长为或2或.
同课章节目录
