吉林省长春市宽城区实验学校(初中部)2023—2024 学年九年级上学期数学学科期初学情调研试卷(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市宽城区实验学校(初中部)2023—2024 学年九年级上学期数学学科期初学情调研试卷(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 582.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 15:48:02 | ||
图片预览


文档简介
长春市宽城区实验学校(初中部)2023—2024 学年
九年级上学期数学学科期初学情调研
班 一、选择题(每小题 3 分,共 24 分)
级
: 1.若二次根式 x + 3 有意义,则 x 的取值范围是
(A)x> 3. (B)x≥ 3. (C)x>3. (D)x≥3.
2.某校 11 名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前 5 名,则他
不仅要知道自己的成绩,还应知道这 11 名学生成绩的
(A).平均数 (B).众数 (C).方差 (D).中位数
b 2 a b
3.若 = ,则 的值是
姓 a 3 a
名
1 1 2 3
: (A) . (B) . (C) . (D) .
3 3 3 5
4. 一元二次方程 x2 + 9 = 0的根的情况是
(A)有两个不相等的实数根. (B)有两个相等的实数根.
(C)没有实数根. (D)只有一个实数根.
5. 如图,△ABC 的面积为 24,将△ABC 沿 BC 平移到△A′B′C′,使 B′ 和 C 重合,连结
AC′, 则△ACC′的面积为
(A)6. (B)8. (C)12. (D)24.
考
A
号
:
D
B
E F C
(第 5 题) (第 6 题) (第 7 题)
6. 某校数学兴趣小组为测量学校旗杆 AC 的高度,在点 F 处竖立一根长为 1 米的标杆
DF ,如图所示,量出DF 的影子EF 的长度为 0.75 米,再量出旗杆 AC 的影子BC 的
长度为6 米,则旗杆 AC 的高度为
(A)4.5 米. (B)7 米. (C)7.5 米. (D)8 米.
7. 欧几里得的《原本》记载,形如 x2+ax=b2 的方程的图解法是:画 Rt△ABC,使∠
ACB=90°,BC= a ,AC=b,再在斜边 AB 上截取 BD= a .则该方程的一个正根是
2 2
(A)AC 的长. (B)AD 的长. (C)BC 的长. (D)CD 的长.
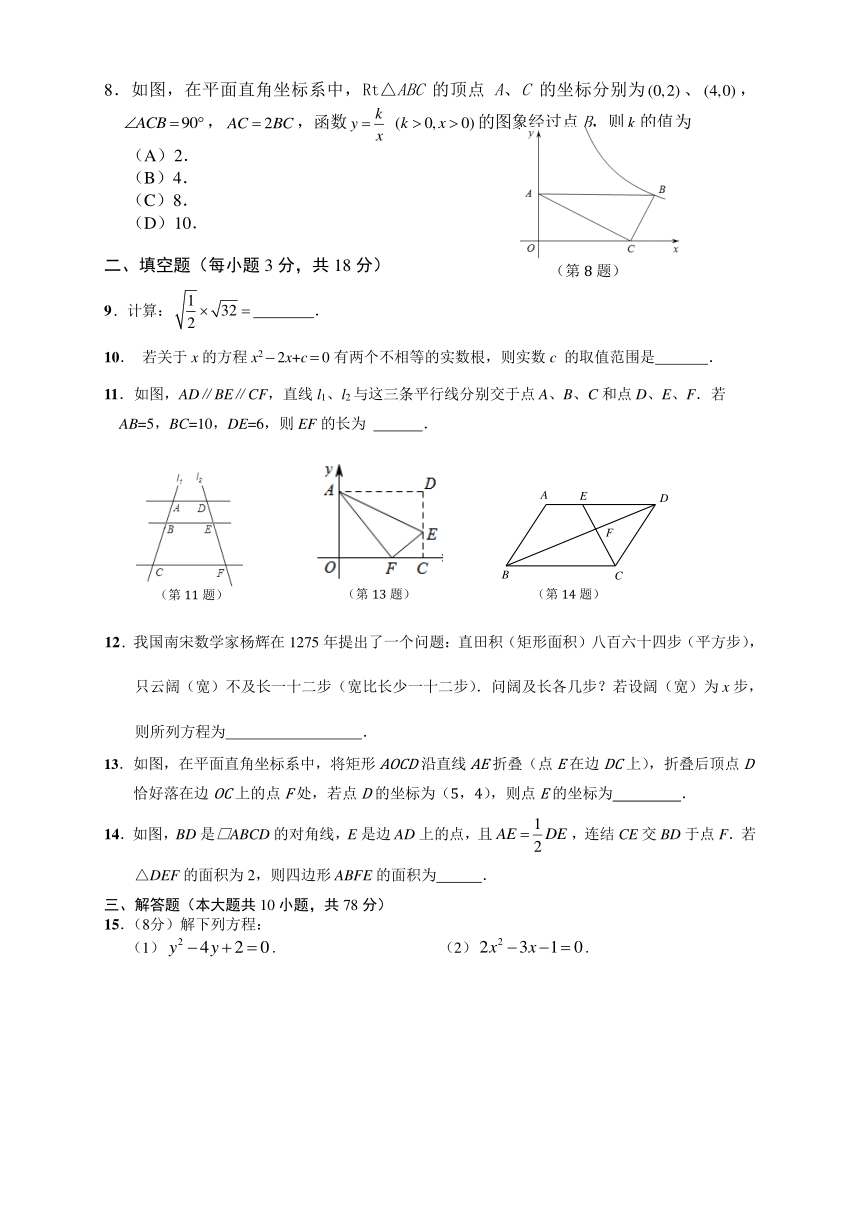
8.如图,在平面直角坐标系中,Rt△ABC 的顶点 A、C 的坐标分别为 (0,2) 、 (4,0) ,
k
ACB =90 , AC = 2BC,函数 y = (k 0, x 0) 的图象经过点 B,则 k 的值为
x
(A)2.
(B)4.
(C)8.
(D)10.
二、填空题(每小题 3 分,共 18 分) (第 8 题)
1
9.计算: 32 = .
2
10. 若关于 x 的方程 x2 2x+c= 0 有两个不相等的实数根,则实数 c 的取值范围是 .
11.如图,AD∥BE∥CF,直线 l1、l2 与这三条平行线分别交于点 A、B、C 和点 D、E、F.若
AB=5,BC=10,DE=6,则 EF 的长为 .
A E
D
F
B C
(第 11 题) (第 13 题) (第 14 题)
12.我国南宋数学家杨辉在 1275 年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),
只云阔(宽)不及长一十二步(宽比长少一十二步).问阔及长各几步?若设阔(宽)为 x 步,
则所列方程为 .
13.如图,在平面直角坐标系中,将矩形 AOCD 沿直线 AE 折叠(点 E 在边 DC 上),折叠后顶点 D
恰好落在边 OC 上的点 F 处,若点 D 的坐标为(5,4),则点 E 的坐标为 .
1
14.如图,BD 是□ABCD 的对角线,E 是边 AD 上的点,且 AE = DE ,连结 CE 交 BD 于点 F.若
2
△DEF 的面积为 2,则四边形 ABFE 的面积为 .
三、解答题(本大题共 10 小题,共 78 分)
15.(8分)解下列方程:
2 2
(1) y 4y + 2 = 0 . (2)2x 3x 1= 0 .
16.(6分)某种植基地2016年蔬菜产量为100吨,预计2018年蔬菜产量达到121吨,求蔬菜产量的年
平均增长率.
17.(6 分)图①、图②均为 4 6的正方形网格,每个小正方形的边长均为 1, ABC的顶点在格
点上.按要求在图①、图②中各画一个三角形.要求:所画的三角形与 ABC相似,且所画三
角形顶点在格点上,与 ABC有公共点B ,且与 ABC的相似比不为 1.
A A
.
B C
B C
图① 图②
(第 17 题)
18.(7 分)将两个完全相同的含有 30°角的直角三角板在同一平面内按如图所示位置摆放.点 A、E、
B、D 依次在同一条线上,连结 AF、CD.
(1)求证:四边形 AFDC 是平行四边形;
(2)己知 BC= 6cm,当四边形 AFDC 是菱形时,AD 的长为 cm.
C
E B
A D
F
(第 18 题)
19.(7 分)近年来,肥胖已经成为影响人们身体健康的重要因素.目前,国际上常用身体质量指数
(Body Mass Index.缩写 BMI)来衡量人体肥胖程度以及是否健康,其计算公式是
体重(单位:kg)
BMI = .
身高(2 单位:m2)
60
例如:某人身高 1.60m,体重 60kg,则他的BMI = 23.4
1.602
中国成人的 BMI 数值标准为:BMI<18.5 为偏瘦;18.5≤BMI<24 为正常;
24≤BMI<28 为偏胖, BMI≥28 为肥胖.
某公司为了解员工的健康情况,随机抽取了一部分员工的体检数据,通过计算得到
他们的 BMI 值并绘制了如下两幅不完整的统计图.
抽取的员工胖瘦程度的条形统计图 抽取的员工胖瘦程度的扇形统计图
人数(人)
10
偏瘦 肥胖
8 7
6
4
3
正常 偏胖
2
2 35%
0 偏瘦 正常 偏胖 肥胖 类别 (第 19 题)
根据以上信息回答下列问题:
(1)补全条形统计图;
(2)请估计该公司 200 名员工中属于偏胖和肥胖的总人数;
(3)基于上述统计结果,公司建议每个人制定健身计划.员工小张身高 1.70m,
BMI 值为 27,他想通过健身减重使自己的 BMI 达到正常,则他的体重至
少要需要减掉 kg.(结果精确到 1 kg)
20.(8 分)某商场以每件 280 元的价格购进一批商品,当每件商品售价为 360 元时,每月可售出
60 件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价 1
元,那么商场每月就可以多售出 5 件.
(1)求降价前商场每月销售该商品的利润.
(2)如果使商场每月销售这种商品的利润达到 7 200 元,且更有利于减少库存,求每件商品应
降价的钱数.
21.(8 分)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行
15 分钟到缆车站,再乘坐缆车直达山项.甲、乙距山脚的垂直高度 y(米)与甲登山的时间 x(分
钟)之间的函数图象如图所示.
(1)当 15≤x≤40 时,求乙距山脚的垂直高度 y 与 x 之间的函数关系式;
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
y(米)
300 甲
乙
160
0 15 25 40 60 x(分钟)
22.(8 分)在矩形 ABCD 中, AD = 3,CD = 4,点 E 在边CD上,且 DE =1.
探究:如图①,点 P 在矩形 ABCD 的边 AD 上,连结 PE ,过点 E 作 EF ⊥ PE ,交边 BC 于点F .求
证: PDE∽ ECF .
PE
应用:如图②,若图①的 EF 交边 AB 于点 F ,其它条件不变,连结 PF,则 的值为 ,若
EF
75
PEF 的面积是 ,则 AP 的长为 .
32
(第 22 题)
23.(9 分)【教材呈现】下面是华师版八年级下册数学教材第 121 页的部分内容.
如图,点 E 是正方形 ABCD 的边 CD 上的一点,点 F 是 CB 的延长线上的一点,且 EA⊥AF.求
证:DE=BF.
结合图①,写出解答的全过程.
【应用】如图②,点 E 是正方形 ABCD 的边 CD 上的一点,点 F 是边 CB 上的一点,∠EAF=45°.若
BF=2,DE=1,则 EF 的长为 .
【拓展】如图③,四边形 ABCD 中,∠B=90°,∠CAD=45°,DE⊥BC 于点 E.若 AB=BE=3,
DE= 10 ,则 BC﹣CD= .
24.(12 分)如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,动点 D 从点 A 出发以每秒 3 个单
位的速度运动至点 B,过点 D 作 DE⊥AB 交射线 AC 于点 E.设点 D 的运动时间为 t 秒( t 0 ).
(1)线段 AE 的长为 .(用含 t 的代数式表示)
(2)若△ADE 与△ACB 的相似比为 1:2时,求 t 的值.
(3)设△ADE 与△ACB 重叠部分图形的周长为 L,求 L 与 t 之间的函数关系式.
(4)当直线 DE 把△ACB 分成的两部分图形中有一个是轴对称图形时,直接写出 t
的值.
(第 24 题)
九年级上学期数学学科期初学情调研
班 一、选择题(每小题 3 分,共 24 分)
级
: 1.若二次根式 x + 3 有意义,则 x 的取值范围是
(A)x> 3. (B)x≥ 3. (C)x>3. (D)x≥3.
2.某校 11 名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前 5 名,则他
不仅要知道自己的成绩,还应知道这 11 名学生成绩的
(A).平均数 (B).众数 (C).方差 (D).中位数
b 2 a b
3.若 = ,则 的值是
姓 a 3 a
名
1 1 2 3
: (A) . (B) . (C) . (D) .
3 3 3 5
4. 一元二次方程 x2 + 9 = 0的根的情况是
(A)有两个不相等的实数根. (B)有两个相等的实数根.
(C)没有实数根. (D)只有一个实数根.
5. 如图,△ABC 的面积为 24,将△ABC 沿 BC 平移到△A′B′C′,使 B′ 和 C 重合,连结
AC′, 则△ACC′的面积为
(A)6. (B)8. (C)12. (D)24.
考
A
号
:
D
B
E F C
(第 5 题) (第 6 题) (第 7 题)
6. 某校数学兴趣小组为测量学校旗杆 AC 的高度,在点 F 处竖立一根长为 1 米的标杆
DF ,如图所示,量出DF 的影子EF 的长度为 0.75 米,再量出旗杆 AC 的影子BC 的
长度为6 米,则旗杆 AC 的高度为
(A)4.5 米. (B)7 米. (C)7.5 米. (D)8 米.
7. 欧几里得的《原本》记载,形如 x2+ax=b2 的方程的图解法是:画 Rt△ABC,使∠
ACB=90°,BC= a ,AC=b,再在斜边 AB 上截取 BD= a .则该方程的一个正根是
2 2
(A)AC 的长. (B)AD 的长. (C)BC 的长. (D)CD 的长.
8.如图,在平面直角坐标系中,Rt△ABC 的顶点 A、C 的坐标分别为 (0,2) 、 (4,0) ,
k
ACB =90 , AC = 2BC,函数 y = (k 0, x 0) 的图象经过点 B,则 k 的值为
x
(A)2.
(B)4.
(C)8.
(D)10.
二、填空题(每小题 3 分,共 18 分) (第 8 题)
1
9.计算: 32 = .
2
10. 若关于 x 的方程 x2 2x+c= 0 有两个不相等的实数根,则实数 c 的取值范围是 .
11.如图,AD∥BE∥CF,直线 l1、l2 与这三条平行线分别交于点 A、B、C 和点 D、E、F.若
AB=5,BC=10,DE=6,则 EF 的长为 .
A E
D
F
B C
(第 11 题) (第 13 题) (第 14 题)
12.我国南宋数学家杨辉在 1275 年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),
只云阔(宽)不及长一十二步(宽比长少一十二步).问阔及长各几步?若设阔(宽)为 x 步,
则所列方程为 .
13.如图,在平面直角坐标系中,将矩形 AOCD 沿直线 AE 折叠(点 E 在边 DC 上),折叠后顶点 D
恰好落在边 OC 上的点 F 处,若点 D 的坐标为(5,4),则点 E 的坐标为 .
1
14.如图,BD 是□ABCD 的对角线,E 是边 AD 上的点,且 AE = DE ,连结 CE 交 BD 于点 F.若
2
△DEF 的面积为 2,则四边形 ABFE 的面积为 .
三、解答题(本大题共 10 小题,共 78 分)
15.(8分)解下列方程:
2 2
(1) y 4y + 2 = 0 . (2)2x 3x 1= 0 .
16.(6分)某种植基地2016年蔬菜产量为100吨,预计2018年蔬菜产量达到121吨,求蔬菜产量的年
平均增长率.
17.(6 分)图①、图②均为 4 6的正方形网格,每个小正方形的边长均为 1, ABC的顶点在格
点上.按要求在图①、图②中各画一个三角形.要求:所画的三角形与 ABC相似,且所画三
角形顶点在格点上,与 ABC有公共点B ,且与 ABC的相似比不为 1.
A A
.
B C
B C
图① 图②
(第 17 题)
18.(7 分)将两个完全相同的含有 30°角的直角三角板在同一平面内按如图所示位置摆放.点 A、E、
B、D 依次在同一条线上,连结 AF、CD.
(1)求证:四边形 AFDC 是平行四边形;
(2)己知 BC= 6cm,当四边形 AFDC 是菱形时,AD 的长为 cm.
C
E B
A D
F
(第 18 题)
19.(7 分)近年来,肥胖已经成为影响人们身体健康的重要因素.目前,国际上常用身体质量指数
(Body Mass Index.缩写 BMI)来衡量人体肥胖程度以及是否健康,其计算公式是
体重(单位:kg)
BMI = .
身高(2 单位:m2)
60
例如:某人身高 1.60m,体重 60kg,则他的BMI = 23.4
1.602
中国成人的 BMI 数值标准为:BMI<18.5 为偏瘦;18.5≤BMI<24 为正常;
24≤BMI<28 为偏胖, BMI≥28 为肥胖.
某公司为了解员工的健康情况,随机抽取了一部分员工的体检数据,通过计算得到
他们的 BMI 值并绘制了如下两幅不完整的统计图.
抽取的员工胖瘦程度的条形统计图 抽取的员工胖瘦程度的扇形统计图
人数(人)
10
偏瘦 肥胖
8 7
6
4
3
正常 偏胖
2
2 35%
0 偏瘦 正常 偏胖 肥胖 类别 (第 19 题)
根据以上信息回答下列问题:
(1)补全条形统计图;
(2)请估计该公司 200 名员工中属于偏胖和肥胖的总人数;
(3)基于上述统计结果,公司建议每个人制定健身计划.员工小张身高 1.70m,
BMI 值为 27,他想通过健身减重使自己的 BMI 达到正常,则他的体重至
少要需要减掉 kg.(结果精确到 1 kg)
20.(8 分)某商场以每件 280 元的价格购进一批商品,当每件商品售价为 360 元时,每月可售出
60 件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价 1
元,那么商场每月就可以多售出 5 件.
(1)求降价前商场每月销售该商品的利润.
(2)如果使商场每月销售这种商品的利润达到 7 200 元,且更有利于减少库存,求每件商品应
降价的钱数.
21.(8 分)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行
15 分钟到缆车站,再乘坐缆车直达山项.甲、乙距山脚的垂直高度 y(米)与甲登山的时间 x(分
钟)之间的函数图象如图所示.
(1)当 15≤x≤40 时,求乙距山脚的垂直高度 y 与 x 之间的函数关系式;
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
y(米)
300 甲
乙
160
0 15 25 40 60 x(分钟)
22.(8 分)在矩形 ABCD 中, AD = 3,CD = 4,点 E 在边CD上,且 DE =1.
探究:如图①,点 P 在矩形 ABCD 的边 AD 上,连结 PE ,过点 E 作 EF ⊥ PE ,交边 BC 于点F .求
证: PDE∽ ECF .
PE
应用:如图②,若图①的 EF 交边 AB 于点 F ,其它条件不变,连结 PF,则 的值为 ,若
EF
75
PEF 的面积是 ,则 AP 的长为 .
32
(第 22 题)
23.(9 分)【教材呈现】下面是华师版八年级下册数学教材第 121 页的部分内容.
如图,点 E 是正方形 ABCD 的边 CD 上的一点,点 F 是 CB 的延长线上的一点,且 EA⊥AF.求
证:DE=BF.
结合图①,写出解答的全过程.
【应用】如图②,点 E 是正方形 ABCD 的边 CD 上的一点,点 F 是边 CB 上的一点,∠EAF=45°.若
BF=2,DE=1,则 EF 的长为 .
【拓展】如图③,四边形 ABCD 中,∠B=90°,∠CAD=45°,DE⊥BC 于点 E.若 AB=BE=3,
DE= 10 ,则 BC﹣CD= .
24.(12 分)如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,动点 D 从点 A 出发以每秒 3 个单
位的速度运动至点 B,过点 D 作 DE⊥AB 交射线 AC 于点 E.设点 D 的运动时间为 t 秒( t 0 ).
(1)线段 AE 的长为 .(用含 t 的代数式表示)
(2)若△ADE 与△ACB 的相似比为 1:2时,求 t 的值.
(3)设△ADE 与△ACB 重叠部分图形的周长为 L,求 L 与 t 之间的函数关系式.
(4)当直线 DE 把△ACB 分成的两部分图形中有一个是轴对称图形时,直接写出 t
的值.
(第 24 题)
同课章节目录
