初中数学华东师大版九上25.2.2频率与概率 课件(共21张PPT)
文档属性
| 名称 | 初中数学华东师大版九上25.2.2频率与概率 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 10:04:06 | ||
图片预览







文档简介
(共21张PPT)
25.2.2
频
率
与
概
率
华师版
九年
级
数
学
课
件
learning target
学习目标
1.会用直接列举法和画树状图或列表法列举所有的等可能结果.
2.体会频率与概率之间的关系,会灵活运用列举法求实际生活中随机事件的概率.
3.发现猜想试验、收集数据、分析结果等过程,体会概率是描述不确定现象规律的数学模型.
重、难点与关键
重点:会用直接列举法和画树状图或列表法列举所有的等可能结果.
难点:体会频率与概率之间的关系,会灵活运用概率公式求实际生活中随机事件的概率.
关键:发现猜想试验、收集数据、分析结果等过程,体会概率是描述不确定现象规律的数学模型.
3.对于这类的等可能性事件,我们可以列举出所有等可能的结果,如果是同时抛掷两枚硬币或骰子,还能用理论分析的方法列举出来吗?
1.抛掷一枚硬币,落地后会出现几种结果?
落地后会出现正面、反面向上这2种等可能性的结果.
2.抛掷一个骰子,它落地时向上的数有几种可能?
落地时向上的数有 1、2、3、4、5、6这6种等可能的结果.
Context import
情境导入
思考:
4.玲玲和倩倩是一对好朋友,她俩都想去观看周杰伦的演唱会,可手里只有一张票,怎么办呢?玲玲对倩倩说:“我向空中抛2枚同样的一元硬币,如果落地后一正一反,就是我去;如果落地后两面一样,就是你去!”你认为这个游戏公平吗?
游戏公平与否实际就是同时抛掷两枚硬币时求:两枚两面一样和两枚两面不一样的概率是否相等的问题.
Self-inquiry
自我探究
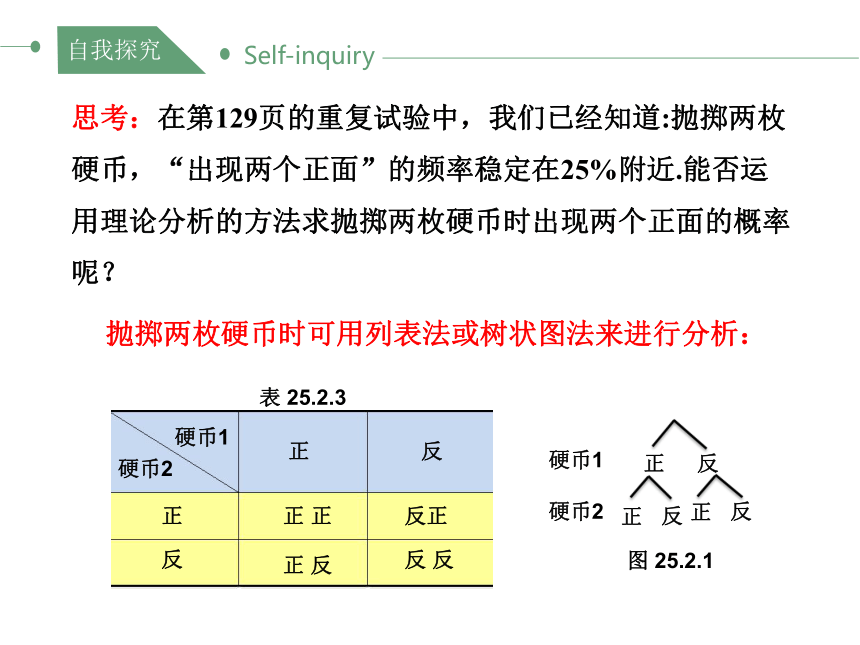
思考:在第129页的重复试验中,我们已经知道:抛掷两枚硬币,“出现两个正面”的频率稳定在25%附近.能否运用理论分析的方法求抛掷两枚硬币时出现两个正面的概率呢?
表 25.2.3
硬币1
硬币2
正
正
反
反
正 正
反正
正 反
反 反
硬币1
硬币2
正
反
正
反
正
反
图 25.2.1
抛掷两枚硬币时可用列表法或树状图法来进行分析:
Self-inquiry
自我探究
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
Self-inquiry
自我探究
可知抛掷两枚硬币共有4个机会均等的结果:“出现两正”、“出现两反”、“出现一正一反”、“出现一反一正”,
因此 P(出现两个正面)=.
解:(1)两枚硬币两面一样包括两面都是正面、两面都是反面,共两种情形,其概率为 = .
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有正反、反正两种情形,其概率为 = .
这种一一列举出所有结果的方法称为直接列举法,即把事件可能出现的结果一一列出.
直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
注意:
Self-inquiry
自我探究
由此,我们可以看到:理论分析与重复试验得到的结论是一致的.
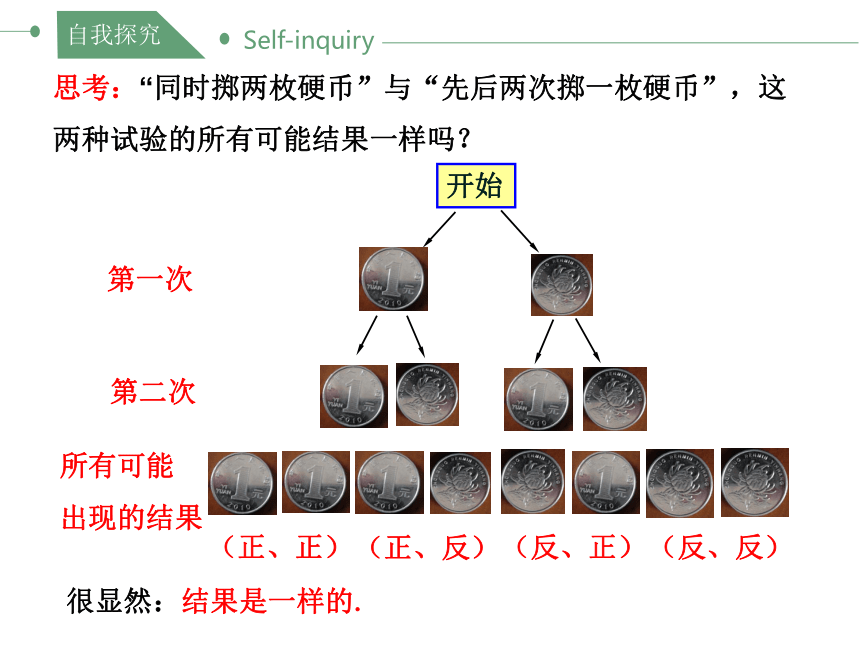
思考:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一次
第二次
所有可能
出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
很显然:结果是一样的.
Self-inquiry
自我探究
随机事件“同时”与“先后”的关系:
“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
归纳:
当一次试验涉及两个因素时,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表或画树状图的办法列举所有结果.
Thinking promotion
思维提升
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
树状图法构造特点:
开始
从上至下每条路径就是一个可能的结果.
Thinking promotion
思维提升
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等.
列表法或树状图法的共同特征:
具有上述特点的试验,我们可以用事件所包含的各种可能的结果数在全部可能的结果数中所占的比,来表示事件发生的概率.
在这些试验中出现的事件为等可能事件.
Thinking promotion
思维提升
5.用力旋转图25. 2. 2所示的转盘甲和转盘乙的指针, 如果想让指针停在蓝色区域,那么选哪个转盘成功的概率比较大?对于这样的题我们又该怎么处理?
Self-inquiry
自我探究
1.有同学说:转盘乙大,相应地,蓝色区域的面积也大,所以选转盘乙成功的概率比较大.你同意吗?
2.还有同学说:每个转盘只有两种颜色,指针不是停在红色区域就是停在蓝色区域,成功的概率都是50%,所以随便选哪个转盘都可以.你同意吗?
如果随着试验次数的增加,两个转盘的指针停在蓝色区域的频率都逐渐稳定下来,那么就容易选择了.
和同学一起做重复试验,将结果填入教材143页表25.2.4,并在图25.2.3中用不同颜色的笔画出相应的两条折线.
观察两个转盘,我们可以发现:两个转盘蓝色区域所对的圆心角都为90°,说明它们都是各占整个转盘的四分之一.
Self-inquiry
自我探究
结合重复试验与理论分析的结果,我们发现
P(小转盘指针停在蓝色区域)=_________
P(大转盘指针停在蓝色区域)=_________
6.将一枚图钉随意向上抛起,求图钉落定后顶尖触地的概率.
虽然图钉被抛起后落定的结果只有两种:“针尖朝上”或“针尖触地”,但由于图针的形状比较特殊,无法预测其具体的概率数值.只能通过重复试验来帮忙.
Self-inquiry
自我探究
通过试验可以看出,试验进行到720次后,频率值稳定在46%左右,我们可以取其作为这个事件发生概率的估计值,即P(顶尖触地)≈46%.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,一般利用频率来估计概率.
在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到的常数,可以估计这个事件发生的概率.
利用频率估计概率
归纳:
Thinking promotion
思维提升
Typical case analysis
典例分析
解题密码:
理解题意直接列出所有的等可能性结果是解题的关键.
例1.若标有A,B,C的三只灯笼按图示悬挂,每次摘取一只(摘B先摘C),直到摘完,则最后一只摘到B的概率是( )
A. B. C. D.
解:由摘取的顺序有ACB,CAB,CBA三种等可能的结果,
∴最后一只摘到B的概率是.
故选:C.
C
Typical case analysis
典例分析
解题密码:
用列表法或树状图法求简单随机事件的概率,列举出所有可能出现的结果是正确解答的关键.
例2.为做好疫情防控工作,某学校门口设置了A,B两条体温快速检测通道,该校两名互不相识的同学王明和李强,随机进入学校,二人恰好均从A通道入校的概率是______ .
解:利用列表法表示所有可能出现的结果如下:
共有4种可能出现的结果,其中二人恰好均从A通道入校的有1种,
所以二人恰好均从A通道入校的概率是 .
故答案为:.
Exchange discussion
交流讨论
解题密码:
通过列表法或树状图法列出所有等可能的结果,再根据概率公式求出事件A或B的概率是解题的关键.
1.某学校在七年级开设了数学史、诗词赏析、编程三门课程,若小明和小颖两名同学每人随机选择其中一门课程,则小明和小颖选到同一门课程的概率是( )
A. B. C. D.
解:画树状图为:(数学史、诗词赏析、编程三门课程分别用A、B、C表示)
共有9种等可能的结果数,其中小明和小颖选到同一门课程的结果数为3,
所以小明和小颖选到同一门课程的概率= = .
故选:B.
B
Exchange discussion
交流讨论
解题密码:
用列表法或画树状图法列出所有均等结果求概率是解题的关键.
2.用如图所示的A、B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成紫色),A转盘是二等分,B转盘是三等分,分别转动两个转盘各一次(指针指向分界线则重新转动转盘),则配成紫色的概率为( )
A. B. C. D.
解:根据题意画树状图如下:
由树状图可知共有6种等可能结果,其中能配成紫色的2种,
∴配成紫色的概率为 = .
故选:C.
C
Classroom summary
课堂小结
1.频率是在试验的基础上得出的,概率从数量上刻画了一个随机事件发生的可能性的大小,它是可以通过计算得出的理论值.频率和概率可能非常接近,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.但并不意味着完全相同.
2.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,用理论分析法求概率时通常用列表法或画树状图法.
谈一谈本节课自己的收获和感受?
25.2.2
频
率
与
概
率
华师版
九年
级
数
学
课
件
learning target
学习目标
1.会用直接列举法和画树状图或列表法列举所有的等可能结果.
2.体会频率与概率之间的关系,会灵活运用列举法求实际生活中随机事件的概率.
3.发现猜想试验、收集数据、分析结果等过程,体会概率是描述不确定现象规律的数学模型.
重、难点与关键
重点:会用直接列举法和画树状图或列表法列举所有的等可能结果.
难点:体会频率与概率之间的关系,会灵活运用概率公式求实际生活中随机事件的概率.
关键:发现猜想试验、收集数据、分析结果等过程,体会概率是描述不确定现象规律的数学模型.
3.对于这类的等可能性事件,我们可以列举出所有等可能的结果,如果是同时抛掷两枚硬币或骰子,还能用理论分析的方法列举出来吗?
1.抛掷一枚硬币,落地后会出现几种结果?
落地后会出现正面、反面向上这2种等可能性的结果.
2.抛掷一个骰子,它落地时向上的数有几种可能?
落地时向上的数有 1、2、3、4、5、6这6种等可能的结果.
Context import
情境导入
思考:
4.玲玲和倩倩是一对好朋友,她俩都想去观看周杰伦的演唱会,可手里只有一张票,怎么办呢?玲玲对倩倩说:“我向空中抛2枚同样的一元硬币,如果落地后一正一反,就是我去;如果落地后两面一样,就是你去!”你认为这个游戏公平吗?
游戏公平与否实际就是同时抛掷两枚硬币时求:两枚两面一样和两枚两面不一样的概率是否相等的问题.
Self-inquiry
自我探究
思考:在第129页的重复试验中,我们已经知道:抛掷两枚硬币,“出现两个正面”的频率稳定在25%附近.能否运用理论分析的方法求抛掷两枚硬币时出现两个正面的概率呢?
表 25.2.3
硬币1
硬币2
正
正
反
反
正 正
反正
正 反
反 反
硬币1
硬币2
正
反
正
反
正
反
图 25.2.1
抛掷两枚硬币时可用列表法或树状图法来进行分析:
Self-inquiry
自我探究
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
Self-inquiry
自我探究
可知抛掷两枚硬币共有4个机会均等的结果:“出现两正”、“出现两反”、“出现一正一反”、“出现一反一正”,
因此 P(出现两个正面)=.
解:(1)两枚硬币两面一样包括两面都是正面、两面都是反面,共两种情形,其概率为 = .
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有正反、反正两种情形,其概率为 = .
这种一一列举出所有结果的方法称为直接列举法,即把事件可能出现的结果一一列出.
直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
注意:
Self-inquiry
自我探究
由此,我们可以看到:理论分析与重复试验得到的结论是一致的.
思考:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一次
第二次
所有可能
出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
很显然:结果是一样的.
Self-inquiry
自我探究
随机事件“同时”与“先后”的关系:
“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
归纳:
当一次试验涉及两个因素时,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表或画树状图的办法列举所有结果.
Thinking promotion
思维提升
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
树状图法构造特点:
开始
从上至下每条路径就是一个可能的结果.
Thinking promotion
思维提升
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等.
列表法或树状图法的共同特征:
具有上述特点的试验,我们可以用事件所包含的各种可能的结果数在全部可能的结果数中所占的比,来表示事件发生的概率.
在这些试验中出现的事件为等可能事件.
Thinking promotion
思维提升
5.用力旋转图25. 2. 2所示的转盘甲和转盘乙的指针, 如果想让指针停在蓝色区域,那么选哪个转盘成功的概率比较大?对于这样的题我们又该怎么处理?
Self-inquiry
自我探究
1.有同学说:转盘乙大,相应地,蓝色区域的面积也大,所以选转盘乙成功的概率比较大.你同意吗?
2.还有同学说:每个转盘只有两种颜色,指针不是停在红色区域就是停在蓝色区域,成功的概率都是50%,所以随便选哪个转盘都可以.你同意吗?
如果随着试验次数的增加,两个转盘的指针停在蓝色区域的频率都逐渐稳定下来,那么就容易选择了.
和同学一起做重复试验,将结果填入教材143页表25.2.4,并在图25.2.3中用不同颜色的笔画出相应的两条折线.
观察两个转盘,我们可以发现:两个转盘蓝色区域所对的圆心角都为90°,说明它们都是各占整个转盘的四分之一.
Self-inquiry
自我探究
结合重复试验与理论分析的结果,我们发现
P(小转盘指针停在蓝色区域)=_________
P(大转盘指针停在蓝色区域)=_________
6.将一枚图钉随意向上抛起,求图钉落定后顶尖触地的概率.
虽然图钉被抛起后落定的结果只有两种:“针尖朝上”或“针尖触地”,但由于图针的形状比较特殊,无法预测其具体的概率数值.只能通过重复试验来帮忙.
Self-inquiry
自我探究
通过试验可以看出,试验进行到720次后,频率值稳定在46%左右,我们可以取其作为这个事件发生概率的估计值,即P(顶尖触地)≈46%.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,一般利用频率来估计概率.
在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到的常数,可以估计这个事件发生的概率.
利用频率估计概率
归纳:
Thinking promotion
思维提升
Typical case analysis
典例分析
解题密码:
理解题意直接列出所有的等可能性结果是解题的关键.
例1.若标有A,B,C的三只灯笼按图示悬挂,每次摘取一只(摘B先摘C),直到摘完,则最后一只摘到B的概率是( )
A. B. C. D.
解:由摘取的顺序有ACB,CAB,CBA三种等可能的结果,
∴最后一只摘到B的概率是.
故选:C.
C
Typical case analysis
典例分析
解题密码:
用列表法或树状图法求简单随机事件的概率,列举出所有可能出现的结果是正确解答的关键.
例2.为做好疫情防控工作,某学校门口设置了A,B两条体温快速检测通道,该校两名互不相识的同学王明和李强,随机进入学校,二人恰好均从A通道入校的概率是______ .
解:利用列表法表示所有可能出现的结果如下:
共有4种可能出现的结果,其中二人恰好均从A通道入校的有1种,
所以二人恰好均从A通道入校的概率是 .
故答案为:.
Exchange discussion
交流讨论
解题密码:
通过列表法或树状图法列出所有等可能的结果,再根据概率公式求出事件A或B的概率是解题的关键.
1.某学校在七年级开设了数学史、诗词赏析、编程三门课程,若小明和小颖两名同学每人随机选择其中一门课程,则小明和小颖选到同一门课程的概率是( )
A. B. C. D.
解:画树状图为:(数学史、诗词赏析、编程三门课程分别用A、B、C表示)
共有9种等可能的结果数,其中小明和小颖选到同一门课程的结果数为3,
所以小明和小颖选到同一门课程的概率= = .
故选:B.
B
Exchange discussion
交流讨论
解题密码:
用列表法或画树状图法列出所有均等结果求概率是解题的关键.
2.用如图所示的A、B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成紫色),A转盘是二等分,B转盘是三等分,分别转动两个转盘各一次(指针指向分界线则重新转动转盘),则配成紫色的概率为( )
A. B. C. D.
解:根据题意画树状图如下:
由树状图可知共有6种等可能结果,其中能配成紫色的2种,
∴配成紫色的概率为 = .
故选:C.
C
Classroom summary
课堂小结
1.频率是在试验的基础上得出的,概率从数量上刻画了一个随机事件发生的可能性的大小,它是可以通过计算得出的理论值.频率和概率可能非常接近,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.但并不意味着完全相同.
2.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,用理论分析法求概率时通常用列表法或画树状图法.
谈一谈本节课自己的收获和感受?
