初中数学华师大版七上5.1.1对顶角学案(含答案)
文档属性
| 名称 | 初中数学华师大版七上5.1.1对顶角学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 11:14:56 | ||
图片预览


文档简介
5.1对顶角 学案
学习目标:
1.能准确理解对顶角的概念,会在具体图形中正确熟练地识别出对顶角。
2.理解对顶角的性质并能运用对顶角的相关知识进行简单的计算。
学习重难点:
【重点】对顶角的定义及性质.
【难点】在具体情境应用对顶角的定义及性质解决实际问题
学习过程:
温故而知新:
什么样的两个角叫互为余角?什么样的两个角叫互为补角?
互余和互补反映的是两个角之间的什么关系?与什么无关?
余角和补角有什么样的性质?
创设情境:
认真观察下面的几幅图形,有没有我们熟悉的几何图形?
从这些图形中我们可见到相交线,平行线,角的众多形象,这一章我们就来研究相交线,平行线及它们构成的角的特征和性质.
探究新知:
自主阅读,获取新知:
阅读课本第160-161页例1的上面回答下列问题:
两条直线相交,有几个交点?直线AB与CD相交,交点为O,还可以怎么叙述?说成“直线AB.CD相交于点O”
(2)两条直线相交形成了哪几个小于180°的角?这几个角之间有哪几对互补的角?根据同角的补角相等,又能得出哪几对相等的角?
(3)将你上述发现填入下面表格中:
角
位置关系
数量关系
(4)什么叫对顶角?需要满足几个条件?
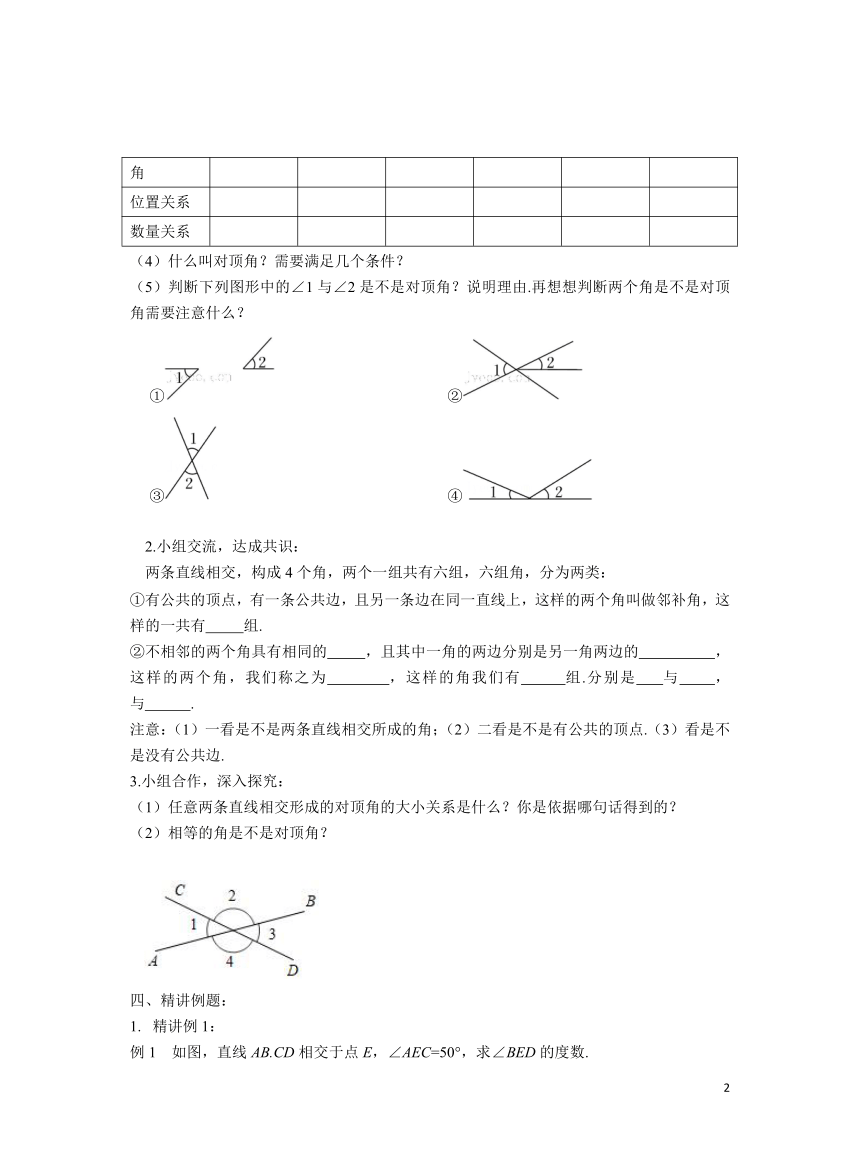
(5)判断下列图形中的∠1与∠2是不是对顶角?说明理由.再想想判断两个角是不是对顶角需要注意什么?
① ②
③ ④
2.小组交流,达成共识:
两条直线相交,构成4个角,两个一组共有六组,六组角,分为两类:
①有公共的顶点,有一条公共边,且另一条边在同一直线上,这样的两个角叫做邻补角,这样的一共有 组.
②不相邻的两个角具有相同的 ,且其中一角的两边分别是另一角两边的 ,这样的两个角,我们称之为 ,这样的角我们有 组.分别是 与 , 与 .
注意:(1)一看是不是两条直线相交所成的角;(2)二看是不是有公共的顶点.(3)看是不是没有公共边.
3.小组合作,深入探究:
(1)任意两条直线相交形成的对顶角的大小关系是什么?你是依据哪句话得到的?
(2)相等的角是不是对顶角?
精讲例题:
精讲例1:
例1 如图,直线AB.CD相交于点E,∠AEC=50°,求∠BED的度数.
分析:先判断两个角的关系,再根据对顶角的性质即可求出.
温馨提示:互为余角互为补角都表示两个角特殊的大小关系,与位置无关.但是对顶角和位置是有关的.
2.精讲例2:
例2 如图,直线AB.CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B.161° C.169° D.138°
分析:本题综合性比较强,先利用对顶角相等求出∠ ,再由角平分线的定义得到得出∠ 度数最后由邻补角的定义,以及进而得出∠ 的度数.
课堂练习:
1.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
3.如图是一把剪刀,若∠AOB+∠COD=60°,则∠AOC= .
4.如图所示,直线AB与CD相交形成了∠1.∠2.∠3和∠4中,若要确定这四个角的度数,至少要测量其中的( )
A.1个角 B.2个角 C.3个角 D.4个角
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是( )
A.∠2增大4° B.∠3增大4° C.∠4增大4° D.∠4减小2°
6.若∠1与∠2互余,∠3与∠2互补,∠4与∠3是对顶角,则∠4与∠1的数量关系是( )
A.∠1=∠4 B.∠4+∠1=90° C.∠1﹣∠4=90° D.∠4﹣∠1=90°
7.如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
8.如图,两条直线a,b相交,∠3=2∠1,则∠2= .
课堂总结:
对顶角的概念及性质
应用对顶角相关知识进行简单计算.
布置作业:
1.162页课后练习1-3题
2.上节课我们学习了余角和补角的知识后,解决了人不能进入围墙内,而测量地面上两堵墙形成的∠AOC的大小,今天你学了对顶角的知识,能不能再想出其他测量办法?
参考答案:
一、温故而知新:
1.两个角的和等于90°(直角),则这两个角互为余角;两个角的和等于180°(平角),则这两个角互为补角.
2.互余和互补表示两个角特殊的大小关系,与位置无关
3.同角(或等角)的余角相等,同角(或等角)的补角相等
三、探究新知:
1.自主阅读,获取新知:
(1)两条直线相交,有1个交点.“直线AB.CD相交于点O”
(2)两条直线相交形成了∠1与∠2.∠3.∠4四个小于180°的角.
(3)将你上述发现填入下面表格中:
角 ∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ∠1与∠3 ∠4与∠2
位置关系 相邻 相邻 相邻 相邻 相对 相对
数量关系 互补 互补 互补 互补 相等 相等
①不是,因为它们不是两条直线相交构成的,②④不是,因为∠1的两条边的反向延长线不是∠2的两条边.③是对顶角.
判断两个角是不是对顶角需要注意
(1)一看是不是两条直线相交所成的角;
(2)二看是不是有公共的顶点.
(3)看是不是没有公共边.
2.小组交流,达成共识:
①4
②顶点,反向延长线,对顶角,2,∠1与∠3,∠4与∠2
3.小组合作,深入探究:
(1)任意两条直线相交形成的对顶角的大小相等,根据同角的补角相等.
(2)相等的角不一定是对顶角.
四、精讲例题:
精讲例1:
例1 如图,直线AB.CD相交于点E,∠AEC=50°,求∠BED的度数.
解:因为直线AB.CD相交于点E,所以∠AEC与∠BED是对顶角,根据对顶角相等,得∠BED=∠AEC=50°,
∠BEC,∠AED=180°-50°=130°
2.精讲例2:
例2 A,BOD,BOM,AOM
五、课堂练习:
1.C
2.A
3.150°
4.A
5.B
6.D
7.D
8.120°
1
学习目标:
1.能准确理解对顶角的概念,会在具体图形中正确熟练地识别出对顶角。
2.理解对顶角的性质并能运用对顶角的相关知识进行简单的计算。
学习重难点:
【重点】对顶角的定义及性质.
【难点】在具体情境应用对顶角的定义及性质解决实际问题
学习过程:
温故而知新:
什么样的两个角叫互为余角?什么样的两个角叫互为补角?
互余和互补反映的是两个角之间的什么关系?与什么无关?
余角和补角有什么样的性质?
创设情境:
认真观察下面的几幅图形,有没有我们熟悉的几何图形?
从这些图形中我们可见到相交线,平行线,角的众多形象,这一章我们就来研究相交线,平行线及它们构成的角的特征和性质.
探究新知:
自主阅读,获取新知:
阅读课本第160-161页例1的上面回答下列问题:
两条直线相交,有几个交点?直线AB与CD相交,交点为O,还可以怎么叙述?说成“直线AB.CD相交于点O”
(2)两条直线相交形成了哪几个小于180°的角?这几个角之间有哪几对互补的角?根据同角的补角相等,又能得出哪几对相等的角?
(3)将你上述发现填入下面表格中:
角
位置关系
数量关系
(4)什么叫对顶角?需要满足几个条件?
(5)判断下列图形中的∠1与∠2是不是对顶角?说明理由.再想想判断两个角是不是对顶角需要注意什么?
① ②
③ ④
2.小组交流,达成共识:
两条直线相交,构成4个角,两个一组共有六组,六组角,分为两类:
①有公共的顶点,有一条公共边,且另一条边在同一直线上,这样的两个角叫做邻补角,这样的一共有 组.
②不相邻的两个角具有相同的 ,且其中一角的两边分别是另一角两边的 ,这样的两个角,我们称之为 ,这样的角我们有 组.分别是 与 , 与 .
注意:(1)一看是不是两条直线相交所成的角;(2)二看是不是有公共的顶点.(3)看是不是没有公共边.
3.小组合作,深入探究:
(1)任意两条直线相交形成的对顶角的大小关系是什么?你是依据哪句话得到的?
(2)相等的角是不是对顶角?
精讲例题:
精讲例1:
例1 如图,直线AB.CD相交于点E,∠AEC=50°,求∠BED的度数.
分析:先判断两个角的关系,再根据对顶角的性质即可求出.
温馨提示:互为余角互为补角都表示两个角特殊的大小关系,与位置无关.但是对顶角和位置是有关的.
2.精讲例2:
例2 如图,直线AB.CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B.161° C.169° D.138°
分析:本题综合性比较强,先利用对顶角相等求出∠ ,再由角平分线的定义得到得出∠ 度数最后由邻补角的定义,以及进而得出∠ 的度数.
课堂练习:
1.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
3.如图是一把剪刀,若∠AOB+∠COD=60°,则∠AOC= .
4.如图所示,直线AB与CD相交形成了∠1.∠2.∠3和∠4中,若要确定这四个角的度数,至少要测量其中的( )
A.1个角 B.2个角 C.3个角 D.4个角
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是( )
A.∠2增大4° B.∠3增大4° C.∠4增大4° D.∠4减小2°
6.若∠1与∠2互余,∠3与∠2互补,∠4与∠3是对顶角,则∠4与∠1的数量关系是( )
A.∠1=∠4 B.∠4+∠1=90° C.∠1﹣∠4=90° D.∠4﹣∠1=90°
7.如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
8.如图,两条直线a,b相交,∠3=2∠1,则∠2= .
课堂总结:
对顶角的概念及性质
应用对顶角相关知识进行简单计算.
布置作业:
1.162页课后练习1-3题
2.上节课我们学习了余角和补角的知识后,解决了人不能进入围墙内,而测量地面上两堵墙形成的∠AOC的大小,今天你学了对顶角的知识,能不能再想出其他测量办法?
参考答案:
一、温故而知新:
1.两个角的和等于90°(直角),则这两个角互为余角;两个角的和等于180°(平角),则这两个角互为补角.
2.互余和互补表示两个角特殊的大小关系,与位置无关
3.同角(或等角)的余角相等,同角(或等角)的补角相等
三、探究新知:
1.自主阅读,获取新知:
(1)两条直线相交,有1个交点.“直线AB.CD相交于点O”
(2)两条直线相交形成了∠1与∠2.∠3.∠4四个小于180°的角.
(3)将你上述发现填入下面表格中:
角 ∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ∠1与∠3 ∠4与∠2
位置关系 相邻 相邻 相邻 相邻 相对 相对
数量关系 互补 互补 互补 互补 相等 相等
①不是,因为它们不是两条直线相交构成的,②④不是,因为∠1的两条边的反向延长线不是∠2的两条边.③是对顶角.
判断两个角是不是对顶角需要注意
(1)一看是不是两条直线相交所成的角;
(2)二看是不是有公共的顶点.
(3)看是不是没有公共边.
2.小组交流,达成共识:
①4
②顶点,反向延长线,对顶角,2,∠1与∠3,∠4与∠2
3.小组合作,深入探究:
(1)任意两条直线相交形成的对顶角的大小相等,根据同角的补角相等.
(2)相等的角不一定是对顶角.
四、精讲例题:
精讲例1:
例1 如图,直线AB.CD相交于点E,∠AEC=50°,求∠BED的度数.
解:因为直线AB.CD相交于点E,所以∠AEC与∠BED是对顶角,根据对顶角相等,得∠BED=∠AEC=50°,
∠BEC,∠AED=180°-50°=130°
2.精讲例2:
例2 A,BOD,BOM,AOM
五、课堂练习:
1.C
2.A
3.150°
4.A
5.B
6.D
7.D
8.120°
1
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
