第23章《旋转》专题卷A——核心考点归纳(含答案)
文档属性
| 名称 | 第23章《旋转》专题卷A——核心考点归纳(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 08:45:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.九年级数学(上)第2章《旋转》专题卷A—核心考点归纳一点通
核心考点1旋转有关的概念
1.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车 C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.如图,△AOB绕着点O旋转至△A'OB'.
(1)点B的对应点是 ;
(2)旋转中心是点 ,旋转角为 ;
(3)∠A的对应角是 ,线段OB的对应线段是线段 .
核心考点2利用旋转求坐标
3.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
A.(3,-3) B.(-3,3) C.(3,3)或(-3,-3) D.(3,-3)或(-3,3)
4.如图,直线y=-与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转60°后得到△AO' B',则点B'的坐标是 .
第2题图 第4题图 第5题图
核心考点3利用旋转求角度
5.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转,得到△AB'C',且C'在BC上,则△B'C'B的度数为( )
A. 56° B. 50° C. 46° D. 40°
6.如图,△ABC中,∠B=70° ,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC,当点B的对应点D恰好落在AC上时,求∠CAE的度数.
7.如图,在Rt△ABC中,∠ACB=90°,在同一平面内,将△ABC绕点C逆时针旋转70°与△EDC重合,恰好使点D在AB上,求∠E的度数.
核心考点4利用旋转求长度
8.如图,在Rt△ABC中,∠ACB= 90°,∠B=60°,BC=2,△A'B'C是由△ABC绕C点顺时针旋转得到,其中点A’与点A是对应点,点B'与点B是对应点,连接AB',且
A,B',A'在同一条直线上,则AA'的长为( )
A. 6 B.4 C. 3 D. 3
9.如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=2,DB=5, DE⊥AC于点E,若△ADE绕点D顺时针旋转90°后,点A,E的对应 点分别为A',F,F恰好在BC边上,求△A'DB的面积.
10.在Rt△ABC中,∠C=90°,AC=1,BC=,点O为Rt△ ABC内一点,连接AO, BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A'O'B(得到A,O的对应点分别为点A',O'),并回答下列问题:∠ABC= ,∠A'BC= , OA+OB+OC= .
核心考点5旋转作图
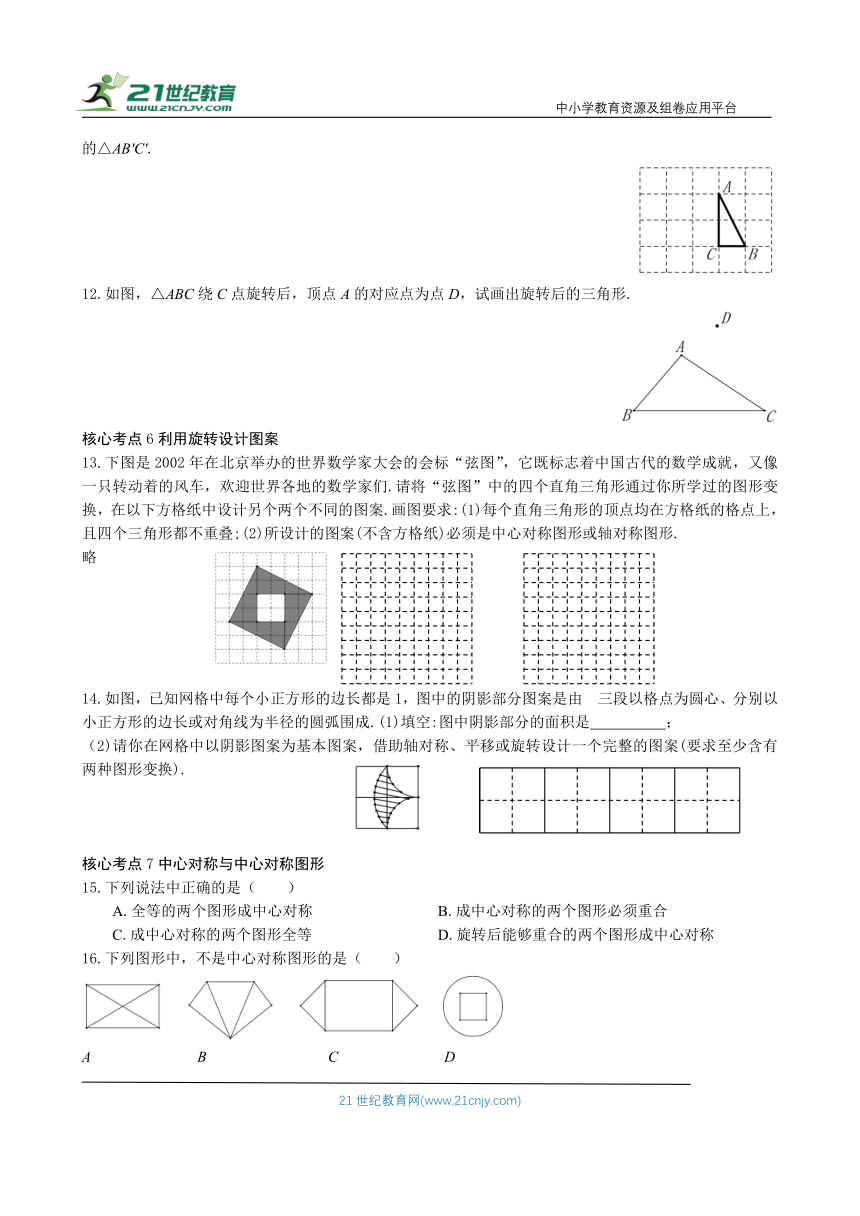
11.如图所示,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB'C'.
12.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试画出旋转后的三角形.
核心考点6利用旋转设计图案
13.下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.请将“弦图”中的四个直角三角形通过你所学过的图形变 换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形都不重叠;(2)所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形.
略
14.如图,已知网格中每个小正方形的边长都是1,图中的阴影部分图案是由 三段以格点为圆心、分别以小正方形的边长或对角线为半径的圆弧围成.(1)填空:图中阴影部分的面积是 ;
(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).
核心考点7中心对称与中心对称图形
15.下列说法中正确的是( )
A.全等的两个图形成中心对称 B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等 D.旋转后能够重合的两个图形成中心对称
16.下列图形中,不是中心对称图形的是( )
A B C D
核心考点8中心对称的性质
17.如图所示,△ABC与△A'B'C’是成中心对称的两个图形,则下列说法不正确的是( )
A. AB=A'B',BC=B'C' B. AB∥A'B',BC∥B'C'
C. S△ABC=S△A'B'C' D.△ABC≌△A'OC'
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB’的长为 .
核心考点9利用中心对称作图
19.如图,已知△ABC和点O.在图中画出△A'B'C’,使△A'B'C’与△ABC关于O点成中心对称.
核心考点10中心对称与点的坐标
20.将点A(3,2)沿x轴向左平移4个单位长度得到点A',则点A'关于原点对称的点的坐标是( )
A.(-3,2) B.(-1,2) C. (1,2) D. (1,-2)
21.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是( )
A. a<-1 B.-1<a< C. -<a<1 D.a>
22.在平面直角坐标系中,点P(2,3)与点P'(2a+b,a+2b)关于原点对称,则a-b的值为 .
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1 ,D三点的坐标分别是(0,4),
(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
核心考点11利用旋转作图与计算
24.如图,已知A(0,4),B(-4,4),C(-4,0),D(0,2).
(1)将线段BD绕B点顺时针旋转90°,请画出BD的对应线段BE;
(2)若F为OC上一点,BF平分四边形ABEO的面积,请直接写出F点坐标.
25.如图,矩形OABC和□ABEF,B(3,4).
(1)画出矩形OABC绕点O逆时针旋转90°后的矩形OA1B1C1,并写出B1的坐标为 ;
(2)若点E的坐标为(5,2),则点F的坐标为 ,请画一条直线l平分矩形OABC与□ABEF组成图形的面积(保留必要的画图痕迹).
26.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2,并写出A2,B2,C2的坐标.
27.如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图1,当BP=BA时,∠EBF= °,猜想∠QFC= °;
(
图
2
)(2)如图2,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(
图
1
)
11.九年级数学(上)第2章《旋转》专题卷A—核心考点归纳一点通
核心考点1旋转有关的概念
1.下列运动形式属于旋转的是( C )
A.在空中上升的氢气球 B.飞驰的火车 C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.如图,△AOB绕着点O旋转至△A'OB'.
(1)点B的对应点是 B' ;
(2)旋转中心是点 O ,旋转角为∠AOA’或∠BOB';
(3)∠A的对应角是∠A',线段OB的对应线段是线段OB' .
核心考点2利用旋转求坐标
3.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( D )
A.(3,-3) B.(-3,3) C. (3,3)或(-3,-3) D. (3,-3)或(-3,3)
4.如图,直线y=-与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转60°后得到△AO' B',则点B'的坐标是 (2,4) .
核心考点3利用旋转求角度
5.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转,得到△AB'C',且C'在BC上,则△B'C'B的度数为( C )
A. 56° B. 50° C. 46° D. 40°
6.如图,△ABC中,∠B=70° ,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC,当
点B的对应点D恰好落在AC上时,求∠CAE的度数.
解: ∠CAE=50°.
7.如图,在Rt△ABC中,∠ACB=90°,在同一平面内,将△ABC绕点C逆时针旋转70°与△EDC重合,恰好使点D在AB上,求∠E的度数.
解:∠E=∠A=35°.
核心考点4利用旋转求长度
8.如图,在Rt△ABC中,∠ACB= 90°,∠B=60°,BC=2,△A'B'C是由△ABC绕C点顺时针旋转得到,其中点A’与点A是对应点,点B'与点B是对应点,连接AB',且
A,B',A'在同一条直线上,则AA'的长为( A )
A. 6 B.4 C. 3 D. 3
9.如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=2,DB=5, DE⊥AC于点E,若△ADE绕点D顺时针旋转90°后,点A,E的对应 点分别为A',F,F恰好在BC边上,求△A'DB的面积.
解:△A'DB的面积是5.
10.在Rt△ABC中,∠C=90°,AC=1,BC=,点O为Rt△ ABC内一点,连接AO, BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A'O'B(得到A,O的对应点分别为点A',O'),并回答下列问题:∠ABC= , ∠A'BC= , OA+OB+OC= .
解:30°, 90°,.
核心考点5旋转作图
11.如图所示,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB'C'.
12.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试画出旋转后的三角形.
核心考点6利用旋转设计图案
13.下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.请将“弦图”中的四个直角三角形通过你所学过的图形变 换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形都不重叠;(2)所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形.
略
14.如图,已知网格中每个小正方形的边长都是1,图中的阴影部分图案是由 三段以格点为圆心、分别以小正方形的边长或对角线为半径的圆弧围成.(1)填空:图中阴影部分的面积是 ;
(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).
提示:(1)1; (2)略.
核心考点7中心对称与中心对称图形
15.下列说法中正确的是( C )
A.全等的两个图形成中心对称 B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等 D.旋转后能够重合的两个图形成中心对称
16.下列图形中,不是中心对称图形的是( B )
A B C D
核心考点8中心对称的性质
17.如图所示,△ABC与△A'B'C’是成中心对称的两个图形,则下列说法不正确的是( D )
A. AB=A'B',BC=B'C' B. AB∥A'B',BC∥B'C'
C. S△ABC=S△A'B'C' D.△ABC≌△A'OC'
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB’的长为 8 .
核心考点9利用中心对称作图
19.如图,已知△ABC和点O.在图中画出△A'B'C’,使△A'B'C’与△ABC关于O点成中心对称.
核心考点10中心对称与点的坐标
20.将点A(3,2)沿x轴向左平移4个单位长度得到点A',则点A'关于原点对称的点的坐标是( D )
A.(-3,2) B.(-1,2) C. (1,2) D. (1,-2)
21.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是( B )
A. a<-1 B.-1<a< C. -<a<1 D.a>
22.在平面直角坐标系中,点P(2,3)与点P'(2a+b,a+2b)关于原点对称,则a-b的值为 1 .
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
解:(1)∵D和D1是对称点,∴对称中心是线段DD1的中点,
∴对称中心的坐标是(0,);
(2)∵已知A,D两点的坐标分别是(0,4),(0,2),∴正方形的边长为2,
∴B(-2,4),C(-2,2),C1(2,3),B1(2,1).
核心考点11利用旋转作图与计算
24.如图,已知A(0,4),B(-4,4),C(-4,0),D(0,2).
(1)将线段BD绕B点顺时针旋转90°,请画出BD的对应线段BE;
(2)若F为OC上一点,BF平分四边形ABEO的面积,请直接写出F点坐标.
解:(1)略; (2)F(-1,0).
25.如图,矩形OABC和□ABEF,B(3,4).
(1)画出矩形OABC绕点O逆时针旋转90°后的矩形OA1B1C1,并写出B1的坐标为 (-4,3) ;
(2)若点E的坐标为(5,2),则点F的坐标为 (5,-2) ,请画一条直线l平分矩形OABC与□ABEF组成图形的面积(保留必要的画图痕迹).
26.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2,并写出A2,B2,C2的坐标.
解:(1)(2)画图略;
(3)A2(5,0),B2(0,1),C2(2,3).
27.如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图1,当BP=BA时,∠EBF= °,猜想∠QFC= °;
(2)如图2,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(
图1
)
(
图2
)
解:(1)30,60;
(2)猜想∠QFC=60°,证明:∠BAP=∠BAE+∠EAP=60°+∠EAP,
∠EAQ=∠QAP+∠EAP=60°+∠EAP,
∴∠BAP=∠EAQ,在△ABP和△AEQ中,AB=AE,∠BAP=∠EAQ, AQ=AP,
∴△ABP≌△AEQ,∴∠AEQ=∠ABP=90°,
∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,
∴∠QFC=∠EBF+∠BEF=30°+30°=60°.
21世纪教育网(www.21cnjy.com)
11.九年级数学(上)第2章《旋转》专题卷A—核心考点归纳一点通
核心考点1旋转有关的概念
1.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车 C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.如图,△AOB绕着点O旋转至△A'OB'.
(1)点B的对应点是 ;
(2)旋转中心是点 ,旋转角为 ;
(3)∠A的对应角是 ,线段OB的对应线段是线段 .
核心考点2利用旋转求坐标
3.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
A.(3,-3) B.(-3,3) C.(3,3)或(-3,-3) D.(3,-3)或(-3,3)
4.如图,直线y=-与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转60°后得到△AO' B',则点B'的坐标是 .
第2题图 第4题图 第5题图
核心考点3利用旋转求角度
5.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转,得到△AB'C',且C'在BC上,则△B'C'B的度数为( )
A. 56° B. 50° C. 46° D. 40°
6.如图,△ABC中,∠B=70° ,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC,当点B的对应点D恰好落在AC上时,求∠CAE的度数.
7.如图,在Rt△ABC中,∠ACB=90°,在同一平面内,将△ABC绕点C逆时针旋转70°与△EDC重合,恰好使点D在AB上,求∠E的度数.
核心考点4利用旋转求长度
8.如图,在Rt△ABC中,∠ACB= 90°,∠B=60°,BC=2,△A'B'C是由△ABC绕C点顺时针旋转得到,其中点A’与点A是对应点,点B'与点B是对应点,连接AB',且
A,B',A'在同一条直线上,则AA'的长为( )
A. 6 B.4 C. 3 D. 3
9.如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=2,DB=5, DE⊥AC于点E,若△ADE绕点D顺时针旋转90°后,点A,E的对应 点分别为A',F,F恰好在BC边上,求△A'DB的面积.
10.在Rt△ABC中,∠C=90°,AC=1,BC=,点O为Rt△ ABC内一点,连接AO, BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A'O'B(得到A,O的对应点分别为点A',O'),并回答下列问题:∠ABC= ,∠A'BC= , OA+OB+OC= .
核心考点5旋转作图
11.如图所示,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB'C'.
12.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试画出旋转后的三角形.
核心考点6利用旋转设计图案
13.下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.请将“弦图”中的四个直角三角形通过你所学过的图形变 换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形都不重叠;(2)所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形.
略
14.如图,已知网格中每个小正方形的边长都是1,图中的阴影部分图案是由 三段以格点为圆心、分别以小正方形的边长或对角线为半径的圆弧围成.(1)填空:图中阴影部分的面积是 ;
(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).
核心考点7中心对称与中心对称图形
15.下列说法中正确的是( )
A.全等的两个图形成中心对称 B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等 D.旋转后能够重合的两个图形成中心对称
16.下列图形中,不是中心对称图形的是( )
A B C D
核心考点8中心对称的性质
17.如图所示,△ABC与△A'B'C’是成中心对称的两个图形,则下列说法不正确的是( )
A. AB=A'B',BC=B'C' B. AB∥A'B',BC∥B'C'
C. S△ABC=S△A'B'C' D.△ABC≌△A'OC'
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB’的长为 .
核心考点9利用中心对称作图
19.如图,已知△ABC和点O.在图中画出△A'B'C’,使△A'B'C’与△ABC关于O点成中心对称.
核心考点10中心对称与点的坐标
20.将点A(3,2)沿x轴向左平移4个单位长度得到点A',则点A'关于原点对称的点的坐标是( )
A.(-3,2) B.(-1,2) C. (1,2) D. (1,-2)
21.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是( )
A. a<-1 B.-1<a< C. -<a<1 D.a>
22.在平面直角坐标系中,点P(2,3)与点P'(2a+b,a+2b)关于原点对称,则a-b的值为 .
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1 ,D三点的坐标分别是(0,4),
(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
核心考点11利用旋转作图与计算
24.如图,已知A(0,4),B(-4,4),C(-4,0),D(0,2).
(1)将线段BD绕B点顺时针旋转90°,请画出BD的对应线段BE;
(2)若F为OC上一点,BF平分四边形ABEO的面积,请直接写出F点坐标.
25.如图,矩形OABC和□ABEF,B(3,4).
(1)画出矩形OABC绕点O逆时针旋转90°后的矩形OA1B1C1,并写出B1的坐标为 ;
(2)若点E的坐标为(5,2),则点F的坐标为 ,请画一条直线l平分矩形OABC与□ABEF组成图形的面积(保留必要的画图痕迹).
26.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2,并写出A2,B2,C2的坐标.
27.如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图1,当BP=BA时,∠EBF= °,猜想∠QFC= °;
(
图
2
)(2)如图2,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(
图
1
)
11.九年级数学(上)第2章《旋转》专题卷A—核心考点归纳一点通
核心考点1旋转有关的概念
1.下列运动形式属于旋转的是( C )
A.在空中上升的氢气球 B.飞驰的火车 C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.如图,△AOB绕着点O旋转至△A'OB'.
(1)点B的对应点是 B' ;
(2)旋转中心是点 O ,旋转角为∠AOA’或∠BOB';
(3)∠A的对应角是∠A',线段OB的对应线段是线段OB' .
核心考点2利用旋转求坐标
3.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( D )
A.(3,-3) B.(-3,3) C. (3,3)或(-3,-3) D. (3,-3)或(-3,3)
4.如图,直线y=-与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转60°后得到△AO' B',则点B'的坐标是 (2,4) .
核心考点3利用旋转求角度
5.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转,得到△AB'C',且C'在BC上,则△B'C'B的度数为( C )
A. 56° B. 50° C. 46° D. 40°
6.如图,△ABC中,∠B=70° ,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC,当
点B的对应点D恰好落在AC上时,求∠CAE的度数.
解: ∠CAE=50°.
7.如图,在Rt△ABC中,∠ACB=90°,在同一平面内,将△ABC绕点C逆时针旋转70°与△EDC重合,恰好使点D在AB上,求∠E的度数.
解:∠E=∠A=35°.
核心考点4利用旋转求长度
8.如图,在Rt△ABC中,∠ACB= 90°,∠B=60°,BC=2,△A'B'C是由△ABC绕C点顺时针旋转得到,其中点A’与点A是对应点,点B'与点B是对应点,连接AB',且
A,B',A'在同一条直线上,则AA'的长为( A )
A. 6 B.4 C. 3 D. 3
9.如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=2,DB=5, DE⊥AC于点E,若△ADE绕点D顺时针旋转90°后,点A,E的对应 点分别为A',F,F恰好在BC边上,求△A'DB的面积.
解:△A'DB的面积是5.
10.在Rt△ABC中,∠C=90°,AC=1,BC=,点O为Rt△ ABC内一点,连接AO, BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A'O'B(得到A,O的对应点分别为点A',O'),并回答下列问题:∠ABC= , ∠A'BC= , OA+OB+OC= .
解:30°, 90°,.
核心考点5旋转作图
11.如图所示,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB'C'.
12.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试画出旋转后的三角形.
核心考点6利用旋转设计图案
13.下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.请将“弦图”中的四个直角三角形通过你所学过的图形变 换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形都不重叠;(2)所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形.
略
14.如图,已知网格中每个小正方形的边长都是1,图中的阴影部分图案是由 三段以格点为圆心、分别以小正方形的边长或对角线为半径的圆弧围成.(1)填空:图中阴影部分的面积是 ;
(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).
提示:(1)1; (2)略.
核心考点7中心对称与中心对称图形
15.下列说法中正确的是( C )
A.全等的两个图形成中心对称 B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等 D.旋转后能够重合的两个图形成中心对称
16.下列图形中,不是中心对称图形的是( B )
A B C D
核心考点8中心对称的性质
17.如图所示,△ABC与△A'B'C’是成中心对称的两个图形,则下列说法不正确的是( D )
A. AB=A'B',BC=B'C' B. AB∥A'B',BC∥B'C'
C. S△ABC=S△A'B'C' D.△ABC≌△A'OC'
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB’的长为 8 .
核心考点9利用中心对称作图
19.如图,已知△ABC和点O.在图中画出△A'B'C’,使△A'B'C’与△ABC关于O点成中心对称.
核心考点10中心对称与点的坐标
20.将点A(3,2)沿x轴向左平移4个单位长度得到点A',则点A'关于原点对称的点的坐标是( D )
A.(-3,2) B.(-1,2) C. (1,2) D. (1,-2)
21.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是( B )
A. a<-1 B.-1<a< C. -<a<1 D.a>
22.在平面直角坐标系中,点P(2,3)与点P'(2a+b,a+2b)关于原点对称,则a-b的值为 1 .
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
解:(1)∵D和D1是对称点,∴对称中心是线段DD1的中点,
∴对称中心的坐标是(0,);
(2)∵已知A,D两点的坐标分别是(0,4),(0,2),∴正方形的边长为2,
∴B(-2,4),C(-2,2),C1(2,3),B1(2,1).
核心考点11利用旋转作图与计算
24.如图,已知A(0,4),B(-4,4),C(-4,0),D(0,2).
(1)将线段BD绕B点顺时针旋转90°,请画出BD的对应线段BE;
(2)若F为OC上一点,BF平分四边形ABEO的面积,请直接写出F点坐标.
解:(1)略; (2)F(-1,0).
25.如图,矩形OABC和□ABEF,B(3,4).
(1)画出矩形OABC绕点O逆时针旋转90°后的矩形OA1B1C1,并写出B1的坐标为 (-4,3) ;
(2)若点E的坐标为(5,2),则点F的坐标为 (5,-2) ,请画一条直线l平分矩形OABC与□ABEF组成图形的面积(保留必要的画图痕迹).
26.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到的△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2,并写出A2,B2,C2的坐标.
解:(1)(2)画图略;
(3)A2(5,0),B2(0,1),C2(2,3).
27.如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图1,当BP=BA时,∠EBF= °,猜想∠QFC= °;
(2)如图2,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(
图1
)
(
图2
)
解:(1)30,60;
(2)猜想∠QFC=60°,证明:∠BAP=∠BAE+∠EAP=60°+∠EAP,
∠EAQ=∠QAP+∠EAP=60°+∠EAP,
∴∠BAP=∠EAQ,在△ABP和△AEQ中,AB=AE,∠BAP=∠EAQ, AQ=AP,
∴△ABP≌△AEQ,∴∠AEQ=∠ABP=90°,
∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,
∴∠QFC=∠EBF+∠BEF=30°+30°=60°.
21世纪教育网(www.21cnjy.com)
同课章节目录
