第23章《旋转》专题卷B——核心思想方法归纳(选用)(含答案)
文档属性
| 名称 | 第23章《旋转》专题卷B——核心思想方法归纳(选用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 415.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 08:48:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
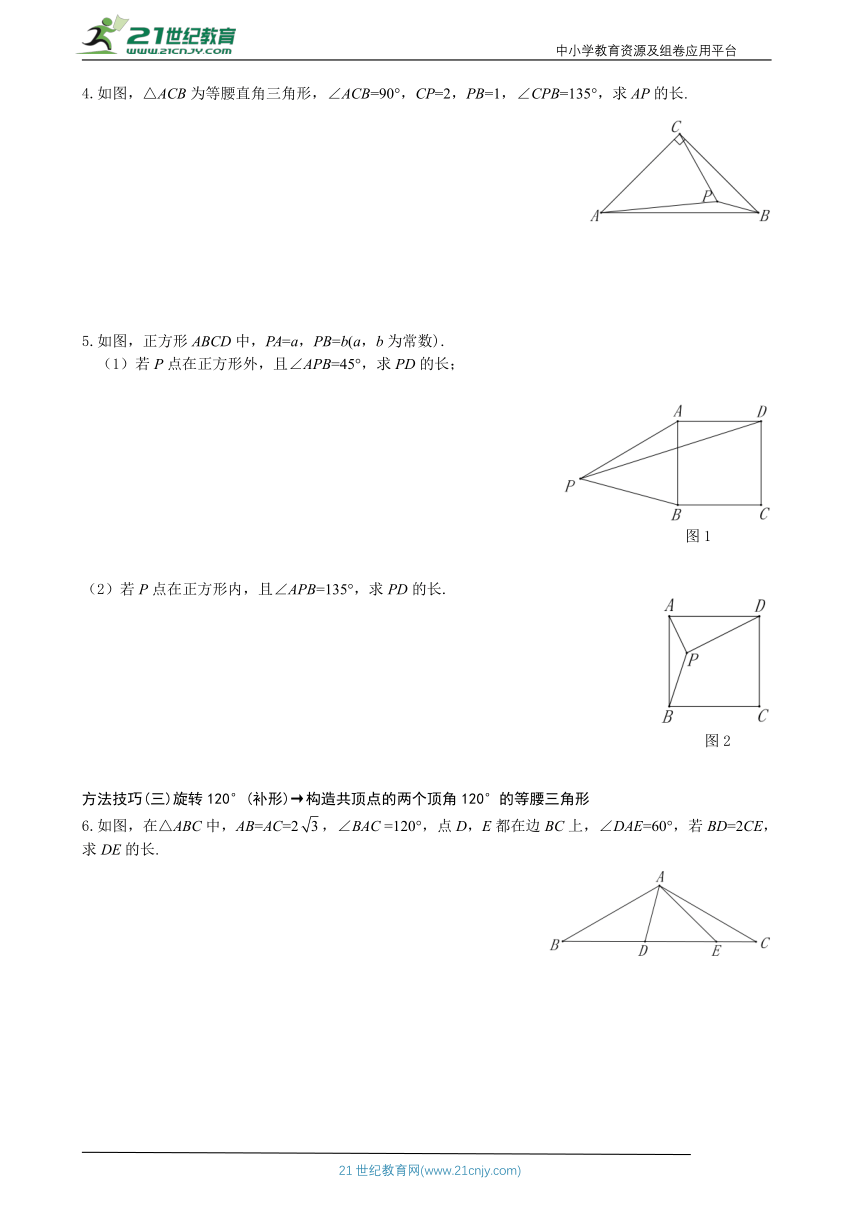
12.九年级数学(上)第23章《旋转》专题卷B
核心思想方法归纳一点通(选用)
核心方法一共顶点的等腰三角形→旋转→构全等
(
图
2
) (
图
1
)基本图形:如图1,在△ABD和△ACE都是等腰直角三角形,∠BAD=∠CAE= 90°,则BE=CD;如图2,△ABD,△ACE都是等边三角形.则BE=DC.
方法技巧(一)旋转60°(补形)→构造共顶点的两个等边三角形
1.如图,△ABC中,∠ABC=30°,AB=6,BC=8,△ACD是等边三角形,求BD的长.
2.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,求S△PAB+S△PAC的值.
方法技巧(二)旋转90°(补形)→构造共顶点的两个等腰直角三角形
3.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=4, CD=3,求BD的长.
4.如图,△ACB为等腰直角三角形,∠ACB=90°,CP=2,PB=1,∠CPB=135°,求AP的长.
5.如图,正方形ABCD中,PA=a,PB=b(a,b为常数).
(1)若P点在正方形外,且∠APB=45°,求PD的长;
(
图
1
)
(
图
2
)(2)若P点在正方形内,且∠APB=135°,求PD的长.
方法技巧(三)旋转120°(补形)→构造共顶点的两个顶角120°的等腰三角形
6.如图,在△ABC中,AB=AC=2,∠BAC =120°,点D,E都在边BC上,∠DAE=60°,若BD=2CE,求DE的长.
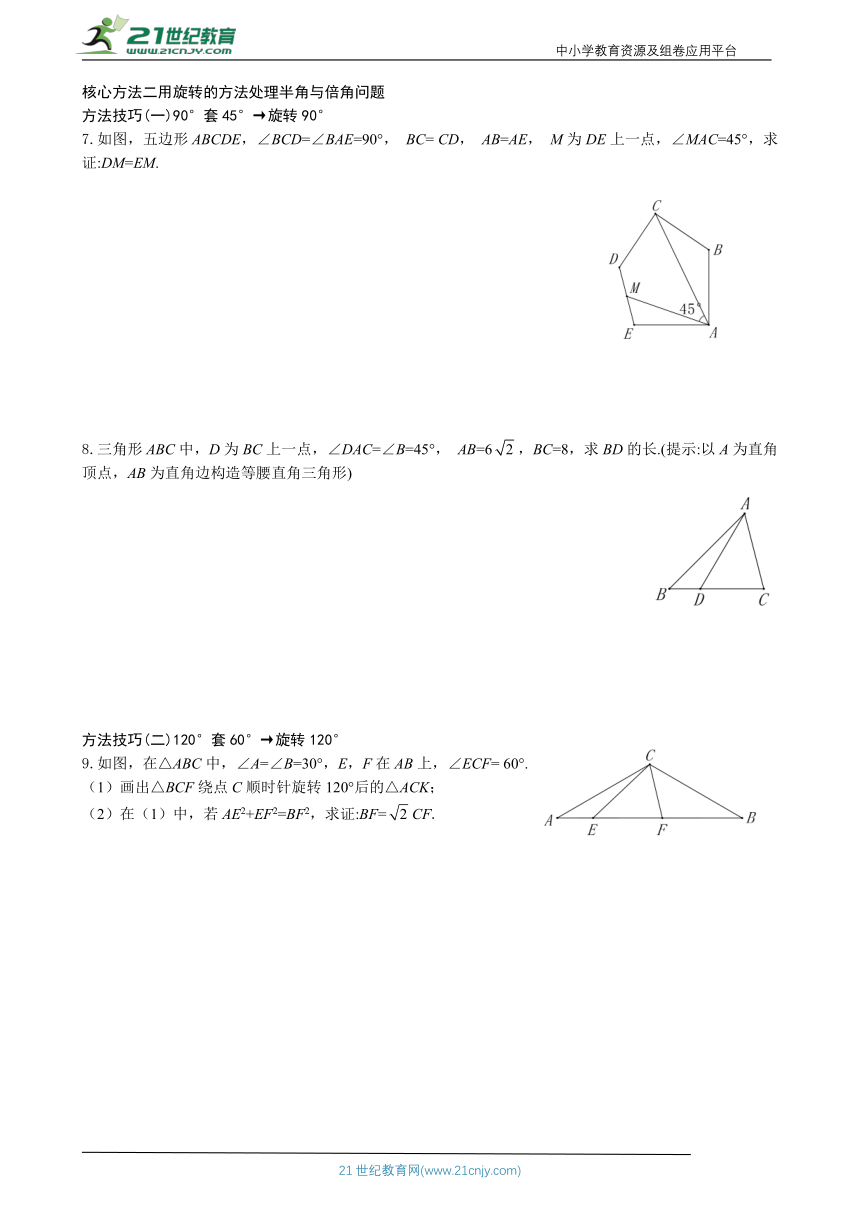
核心方法二用旋转的方法处理半角与倍角问题
方法技巧(一)90°套45°→旋转90°
7.如图,五边形ABCDE,∠BCD=∠BAE=90°, BC= CD, AB=AE, M为DE上一点,∠MAC=45°,求证:DM=EM.
8.三角形ABC中,D为BC上一点,∠DAC=∠B=45°, AB=6,BC=8,求BD的长.(提示:以A为直角顶点,AB为直角边构造等腰直角三角形)
方法技巧(二)120°套60°→旋转120°
9.如图,在△ABC中,∠A=∠B=30°,E,F在AB上,∠ECF= 60°.
(1)画出△BCF绕点C顺时针旋转120°后的△ACK;
(2)在(1)中,若AE2+EF2=BF2,求证:BF=CF.
核心方法三用旋转的方法求最值
方法技巧:旋转→化散为聚→运用三边关系求最值
10.如图,△ABC和△BEF都是等腰直角三角形,∠BAC=∠BEF=90°,BE=2,AB=5,O为CF的中点,将△BEF绕点B旋转的过程中,求AO的最大值与最小值.
11.如图,△ABC中,AB=,AC=3,以C为直角顶点,BC为直角边,向下一作等腰Rt△BCD,求AD的最大值.
12.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请求出线段AM长的最大值及此时点P的坐标.
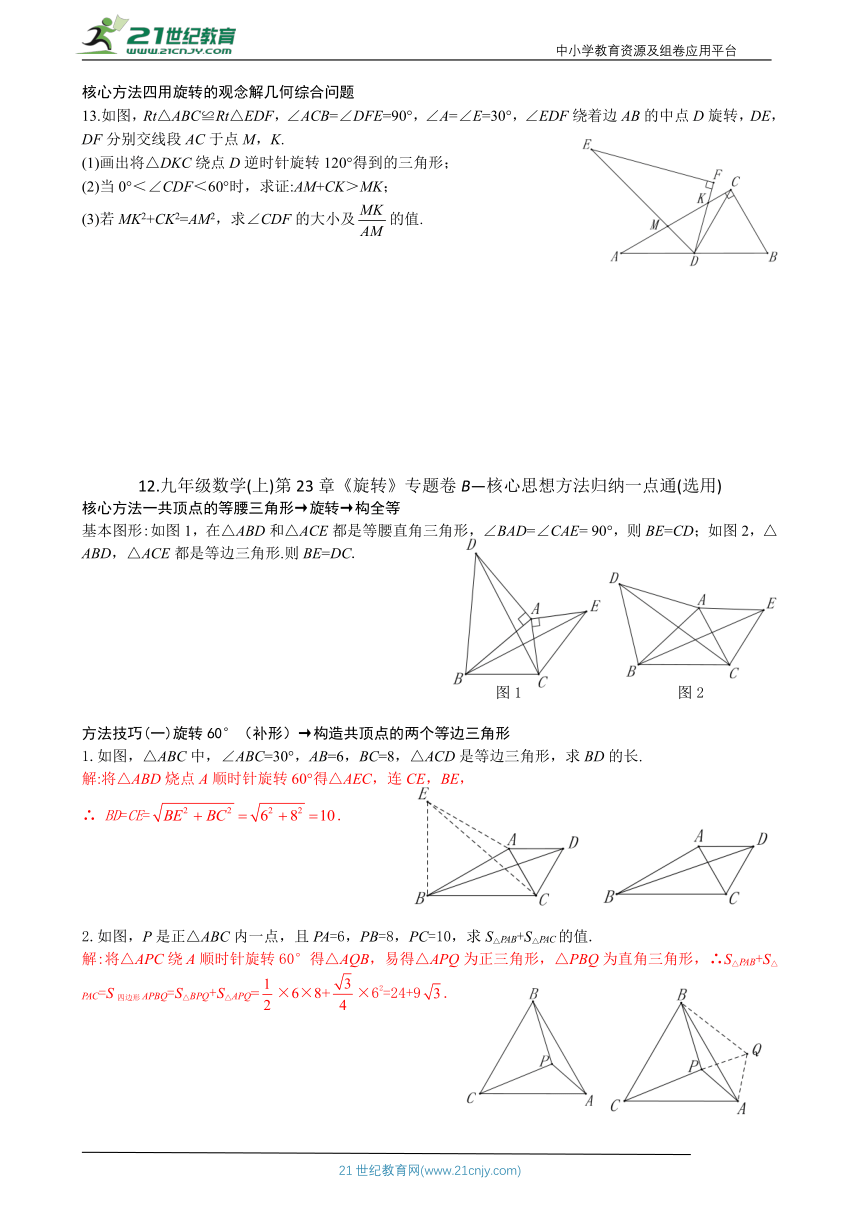
核心方法四用旋转的观念解几何综合问题
13.如图,Rt△ABC≌Rt△EDF,∠ACB=∠DFE=90°,∠A=∠E=30°,∠EDF绕着边AB的中点D旋转,DE, DF分别交线段AC于点M,K.
(1)画出将△DKC绕点D逆时针旋转120°得到的三角形;
(2)当0°<∠CDF<60°时,求证:AM+CK>MK;
(3)若MK2+CK2=AM2,求∠CDF的大小及的值.
12.九年级数学(上)第23章《旋转》专题卷B—核心思想方法归纳一点通(选用)
核心方法一共顶点的等腰三角形→旋转→构全等
(
图2
) (
图1
)基本图形:如图1,在△ABD和△ACE都是等腰直角三角形,∠BAD=∠CAE= 90°,则BE=CD;如图2,△ABD,△ACE都是等边三角形.则BE=DC.
方法技巧(一)旋转60°(补形)→构造共顶点的两个等边三角形
1.如图,△ABC中,∠ABC=30°,AB=6,BC=8,△ACD是等边三角形,求BD的长.
解:将△ABD烧点A顺时针旋转60°得△AEC,连CE,BE,
∴ BD=CE=.
2.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,求S△PAB+S△PAC的值.
解:将△APC绕A顺时针旋转60°得△AQB,易得△APQ为正三角形,△PBQ为直角三角形,∴S△PAB+S△PAC=S四边形APBQ=S△BPQ+S△APQ=×6×8+×62=24+9.
方法技巧(二)旋转90°(补形)→构造共顶点的两个等腰直角三角形
3.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=4, CD=3,求BD的长.
解:将△ABD绕点A顺时针旋转90°得△ACD',连 DD',
则△BAD≌△CAD’,易证∠CDD'=90°, DD'=AD=4,
∴CD'===BD.
4.如图,△ACB为等腰直角三角形,∠ACB=90°,CP=2,PB=1,∠CPB=135°,求AP的长.
解:将△ACP绕点C逆时针旋转90°得△BCE,连EP,则 △CBE≌△ACP, PE2=8,PB2=1,∴BE=PA=3.
5.如图,正方形ABCD中,PA=a,PB=b(a,b为常数).
(1)若P点在正方形外,且∠APB=45°,求PD的长;
(
图1
)解:作AH⊥AP且AH=AP(即将△APD绕A点顺时针旋转90°)△APD≌△ABH,∴PD=BH=;
(
图1
)
(
图2
) (
图1
)(2)若P点在正方形内,且∠APB=135°,求PD的长.
解:方法同上,PD=.
方法技巧(三)旋转120°(补形)→构造共顶点的两个顶角120°的等腰三角形
6.如图,在△ABC中,AB=AC=2,∠BAC =120°,点D,E都在边BC上,∠DAE=60°,若BD=2CE,求DE的长.
解:将△ABD绕点A逆时针旋转120°得△ACF;可证△ADE≌△AFE,DE=EF,CF=BD,∠ACD=∠B=30°,∠FGE=60°,作EH⊥GF于H.设BD=2CE=4x.则CH=x,CF=4x,FH=3x,EH=3x,FE2=FH2+EH2,(6-6x)2=(3x)2+(x)2,解得x1=,x2=(舍去),∴DE=6-6x=3-3.
核心方法二用旋转的方法处理半角与倍角问题
方法技巧(一)90°套45°→旋转90°
7.如图,五边形ABCDE,∠BCD=∠BAE=90°, BC= CD, AB=AE, M为DE上一点,∠MAC=45°,求证:DM=EM.
解:将△CAB绕点C顺时针旋转90°得△CDH,连HM,易证H,M,A共线,△DHM≌△EAM,∴DM=EM.
8.三角形ABC中,D为BC上一点,∠DAC=∠B=45°, AB=6,BC=8,求BD的长.(提示:以A为直角顶点,AB为直角边构造等腰直角三角形)
解:作AE⊥AB交BC的延长线于E,将△ABD绕点A逆时针
旋转90°得△AEF,易求BE=12,易证CD=CF,设BD=x=EF,
则DC=CF=8-x,CE=4,在△CEF中,x2+42=(8-x)2,x=3,
∴BD=3.
方法技巧(二)120°套60°→旋转120°
9.如图,在△ABC中,∠A=∠B=30°,E,F在AB上,∠ECF= 60°.
(1)画出△BCF绕点C顺时针旋转120°后的△ACK;
(2)在(1)中,若AE2+EF2=BF2,求证:BF=CF.
解:(1)略;
(2)连KE,作KQ⊥AC于Q,∵BF=AK,∴AE2+EF2=AK2.
∵∠KCF=∠ACB=120°,∠KCE=60°,∴∠KCE=∠ECF.
∴△KCE≌△FCE(SAS).∴EF=KE,∴AE2+KE2=AK2,
∴∠AEK=90°,∴∠KEC=∠FEC=45°.
∵∠CAE=30°,∴∠ACE=15°.
∴∠KCA=60°-15°=45°,∴KC=KQ.
∵∠KAQ=30°,∴AK= 2KQ,∴AK=KC,BF=CF.
核心方法三用旋转的方法求最值
方法技巧:旋转→化散为聚→运用三边关系求最值
10.如图,△ABC和△BEF都是等腰直角三角形,∠BAC=∠BEF=90°,BE=2,AB=5,O为CF的中点,将△BEF绕点B旋转的过程中,求AO的最大值与最小值.
解:取BC的中点G,连接AG,OG,则OG=BF=,AG=BC=,
∵AG-OG≤AO≤AG+OG,∴≤AO≤,∴当A,O,G共线时,
(
图②
) (
图①
)AO有最大值 (见图①),有最小值 (见图②).
11.如图,△ABC中,AB=,AC=3,以C为直角顶点,BC为直角边,向下一作等腰Rt△BCD,求AD的最大值.
解:将△ACD绕点C顺时针旋转90°得△A'CB,连接AA',则△AA’C为等腰直角三角形,∴AA'=AC=3,
AD=A'B,∵A'B<AB+AA',故当点B,A,A’三点共线时,A'B最大,此时A'B=AB+AA'=+3=4,
∴AD的最大值为4.
12.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请求出线段AM长的最大值及此时点P的坐标.
解:如图,将△MAP烧点P顺时针旋转90°得△BNP,
则△BNP≌△MAP,NB=AM,易得△APN是等腰直角三角形,AP=2,∴AN=2,在△BNA中,
3-2≤BN≤3+2,∴线段AM长的最大值为3+2;此时点N在BA的延长线上,过点P作
PE⊥x轴于点E,PE=AE=,又A(2,0),∴P(2-,).
核心方法四用旋转的观念解几何综合问题
13.如图,Rt△ABC≌Rt△EDF,∠ACB=∠DFE=90°,∠A=∠E=30°,∠EDF绕着边AB的中点D旋转,DE, DF分别交线段AC于点M,K.
(1)画出将△DKC绕点D逆时针旋转120°得到的三角形;
(2)当0°<∠CDF<60°时,求证:AM+CK>MK;
(3)若MK2+CK2=AM2,求∠CDF的大小及的值.
解:(1)作DK'=DK,且∠KDK'=120°,△ADK’即为所求的三角形;
(2)易证△DMK≌△DMK',∴MK=MK',∴AM+CK=AM+AK'>MK',∴AM+CK>MK;
(3)由(1)(2)得MK2+CK2=MK'2 +AK'2=AM2,∴∠AK'M=90°,∵∠MAK'=60°,
∴∠AMK'=30°,∴∠K'MD=∠KMD=75°,∴∠KCD=30°,∴∠KDC=15°,易求.
21世纪教育网(www.21cnjy.com)
12.九年级数学(上)第23章《旋转》专题卷B
核心思想方法归纳一点通(选用)
核心方法一共顶点的等腰三角形→旋转→构全等
(
图
2
) (
图
1
)基本图形:如图1,在△ABD和△ACE都是等腰直角三角形,∠BAD=∠CAE= 90°,则BE=CD;如图2,△ABD,△ACE都是等边三角形.则BE=DC.
方法技巧(一)旋转60°(补形)→构造共顶点的两个等边三角形
1.如图,△ABC中,∠ABC=30°,AB=6,BC=8,△ACD是等边三角形,求BD的长.
2.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,求S△PAB+S△PAC的值.
方法技巧(二)旋转90°(补形)→构造共顶点的两个等腰直角三角形
3.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=4, CD=3,求BD的长.
4.如图,△ACB为等腰直角三角形,∠ACB=90°,CP=2,PB=1,∠CPB=135°,求AP的长.
5.如图,正方形ABCD中,PA=a,PB=b(a,b为常数).
(1)若P点在正方形外,且∠APB=45°,求PD的长;
(
图
1
)
(
图
2
)(2)若P点在正方形内,且∠APB=135°,求PD的长.
方法技巧(三)旋转120°(补形)→构造共顶点的两个顶角120°的等腰三角形
6.如图,在△ABC中,AB=AC=2,∠BAC =120°,点D,E都在边BC上,∠DAE=60°,若BD=2CE,求DE的长.
核心方法二用旋转的方法处理半角与倍角问题
方法技巧(一)90°套45°→旋转90°
7.如图,五边形ABCDE,∠BCD=∠BAE=90°, BC= CD, AB=AE, M为DE上一点,∠MAC=45°,求证:DM=EM.
8.三角形ABC中,D为BC上一点,∠DAC=∠B=45°, AB=6,BC=8,求BD的长.(提示:以A为直角顶点,AB为直角边构造等腰直角三角形)
方法技巧(二)120°套60°→旋转120°
9.如图,在△ABC中,∠A=∠B=30°,E,F在AB上,∠ECF= 60°.
(1)画出△BCF绕点C顺时针旋转120°后的△ACK;
(2)在(1)中,若AE2+EF2=BF2,求证:BF=CF.
核心方法三用旋转的方法求最值
方法技巧:旋转→化散为聚→运用三边关系求最值
10.如图,△ABC和△BEF都是等腰直角三角形,∠BAC=∠BEF=90°,BE=2,AB=5,O为CF的中点,将△BEF绕点B旋转的过程中,求AO的最大值与最小值.
11.如图,△ABC中,AB=,AC=3,以C为直角顶点,BC为直角边,向下一作等腰Rt△BCD,求AD的最大值.
12.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请求出线段AM长的最大值及此时点P的坐标.
核心方法四用旋转的观念解几何综合问题
13.如图,Rt△ABC≌Rt△EDF,∠ACB=∠DFE=90°,∠A=∠E=30°,∠EDF绕着边AB的中点D旋转,DE, DF分别交线段AC于点M,K.
(1)画出将△DKC绕点D逆时针旋转120°得到的三角形;
(2)当0°<∠CDF<60°时,求证:AM+CK>MK;
(3)若MK2+CK2=AM2,求∠CDF的大小及的值.
12.九年级数学(上)第23章《旋转》专题卷B—核心思想方法归纳一点通(选用)
核心方法一共顶点的等腰三角形→旋转→构全等
(
图2
) (
图1
)基本图形:如图1,在△ABD和△ACE都是等腰直角三角形,∠BAD=∠CAE= 90°,则BE=CD;如图2,△ABD,△ACE都是等边三角形.则BE=DC.
方法技巧(一)旋转60°(补形)→构造共顶点的两个等边三角形
1.如图,△ABC中,∠ABC=30°,AB=6,BC=8,△ACD是等边三角形,求BD的长.
解:将△ABD烧点A顺时针旋转60°得△AEC,连CE,BE,
∴ BD=CE=.
2.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,求S△PAB+S△PAC的值.
解:将△APC绕A顺时针旋转60°得△AQB,易得△APQ为正三角形,△PBQ为直角三角形,∴S△PAB+S△PAC=S四边形APBQ=S△BPQ+S△APQ=×6×8+×62=24+9.
方法技巧(二)旋转90°(补形)→构造共顶点的两个等腰直角三角形
3.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=4, CD=3,求BD的长.
解:将△ABD绕点A顺时针旋转90°得△ACD',连 DD',
则△BAD≌△CAD’,易证∠CDD'=90°, DD'=AD=4,
∴CD'===BD.
4.如图,△ACB为等腰直角三角形,∠ACB=90°,CP=2,PB=1,∠CPB=135°,求AP的长.
解:将△ACP绕点C逆时针旋转90°得△BCE,连EP,则 △CBE≌△ACP, PE2=8,PB2=1,∴BE=PA=3.
5.如图,正方形ABCD中,PA=a,PB=b(a,b为常数).
(1)若P点在正方形外,且∠APB=45°,求PD的长;
(
图1
)解:作AH⊥AP且AH=AP(即将△APD绕A点顺时针旋转90°)△APD≌△ABH,∴PD=BH=;
(
图1
)
(
图2
) (
图1
)(2)若P点在正方形内,且∠APB=135°,求PD的长.
解:方法同上,PD=.
方法技巧(三)旋转120°(补形)→构造共顶点的两个顶角120°的等腰三角形
6.如图,在△ABC中,AB=AC=2,∠BAC =120°,点D,E都在边BC上,∠DAE=60°,若BD=2CE,求DE的长.
解:将△ABD绕点A逆时针旋转120°得△ACF;可证△ADE≌△AFE,DE=EF,CF=BD,∠ACD=∠B=30°,∠FGE=60°,作EH⊥GF于H.设BD=2CE=4x.则CH=x,CF=4x,FH=3x,EH=3x,FE2=FH2+EH2,(6-6x)2=(3x)2+(x)2,解得x1=,x2=(舍去),∴DE=6-6x=3-3.
核心方法二用旋转的方法处理半角与倍角问题
方法技巧(一)90°套45°→旋转90°
7.如图,五边形ABCDE,∠BCD=∠BAE=90°, BC= CD, AB=AE, M为DE上一点,∠MAC=45°,求证:DM=EM.
解:将△CAB绕点C顺时针旋转90°得△CDH,连HM,易证H,M,A共线,△DHM≌△EAM,∴DM=EM.
8.三角形ABC中,D为BC上一点,∠DAC=∠B=45°, AB=6,BC=8,求BD的长.(提示:以A为直角顶点,AB为直角边构造等腰直角三角形)
解:作AE⊥AB交BC的延长线于E,将△ABD绕点A逆时针
旋转90°得△AEF,易求BE=12,易证CD=CF,设BD=x=EF,
则DC=CF=8-x,CE=4,在△CEF中,x2+42=(8-x)2,x=3,
∴BD=3.
方法技巧(二)120°套60°→旋转120°
9.如图,在△ABC中,∠A=∠B=30°,E,F在AB上,∠ECF= 60°.
(1)画出△BCF绕点C顺时针旋转120°后的△ACK;
(2)在(1)中,若AE2+EF2=BF2,求证:BF=CF.
解:(1)略;
(2)连KE,作KQ⊥AC于Q,∵BF=AK,∴AE2+EF2=AK2.
∵∠KCF=∠ACB=120°,∠KCE=60°,∴∠KCE=∠ECF.
∴△KCE≌△FCE(SAS).∴EF=KE,∴AE2+KE2=AK2,
∴∠AEK=90°,∴∠KEC=∠FEC=45°.
∵∠CAE=30°,∴∠ACE=15°.
∴∠KCA=60°-15°=45°,∴KC=KQ.
∵∠KAQ=30°,∴AK= 2KQ,∴AK=KC,BF=CF.
核心方法三用旋转的方法求最值
方法技巧:旋转→化散为聚→运用三边关系求最值
10.如图,△ABC和△BEF都是等腰直角三角形,∠BAC=∠BEF=90°,BE=2,AB=5,O为CF的中点,将△BEF绕点B旋转的过程中,求AO的最大值与最小值.
解:取BC的中点G,连接AG,OG,则OG=BF=,AG=BC=,
∵AG-OG≤AO≤AG+OG,∴≤AO≤,∴当A,O,G共线时,
(
图②
) (
图①
)AO有最大值 (见图①),有最小值 (见图②).
11.如图,△ABC中,AB=,AC=3,以C为直角顶点,BC为直角边,向下一作等腰Rt△BCD,求AD的最大值.
解:将△ACD绕点C顺时针旋转90°得△A'CB,连接AA',则△AA’C为等腰直角三角形,∴AA'=AC=3,
AD=A'B,∵A'B<AB+AA',故当点B,A,A’三点共线时,A'B最大,此时A'B=AB+AA'=+3=4,
∴AD的最大值为4.
12.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请求出线段AM长的最大值及此时点P的坐标.
解:如图,将△MAP烧点P顺时针旋转90°得△BNP,
则△BNP≌△MAP,NB=AM,易得△APN是等腰直角三角形,AP=2,∴AN=2,在△BNA中,
3-2≤BN≤3+2,∴线段AM长的最大值为3+2;此时点N在BA的延长线上,过点P作
PE⊥x轴于点E,PE=AE=,又A(2,0),∴P(2-,).
核心方法四用旋转的观念解几何综合问题
13.如图,Rt△ABC≌Rt△EDF,∠ACB=∠DFE=90°,∠A=∠E=30°,∠EDF绕着边AB的中点D旋转,DE, DF分别交线段AC于点M,K.
(1)画出将△DKC绕点D逆时针旋转120°得到的三角形;
(2)当0°<∠CDF<60°时,求证:AM+CK>MK;
(3)若MK2+CK2=AM2,求∠CDF的大小及的值.
解:(1)作DK'=DK,且∠KDK'=120°,△ADK’即为所求的三角形;
(2)易证△DMK≌△DMK',∴MK=MK',∴AM+CK=AM+AK'>MK',∴AM+CK>MK;
(3)由(1)(2)得MK2+CK2=MK'2 +AK'2=AM2,∴∠AK'M=90°,∵∠MAK'=60°,
∴∠AMK'=30°,∴∠K'MD=∠KMD=75°,∴∠KCD=30°,∴∠KDC=15°,易求.
21世纪教育网(www.21cnjy.com)
同课章节目录
