人教版九年级数学(上)第23章《旋转》单元检测卷(含答案)
文档属性
| 名称 | 人教版九年级数学(上)第23章《旋转》单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 835.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 22:12:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
13九年级数学(上)第23章《旋转》单元检测卷
(考试范围:第23章综合测试解答考时间:120分钟满分:120分)
一、选择题(每小题3分,共30分)
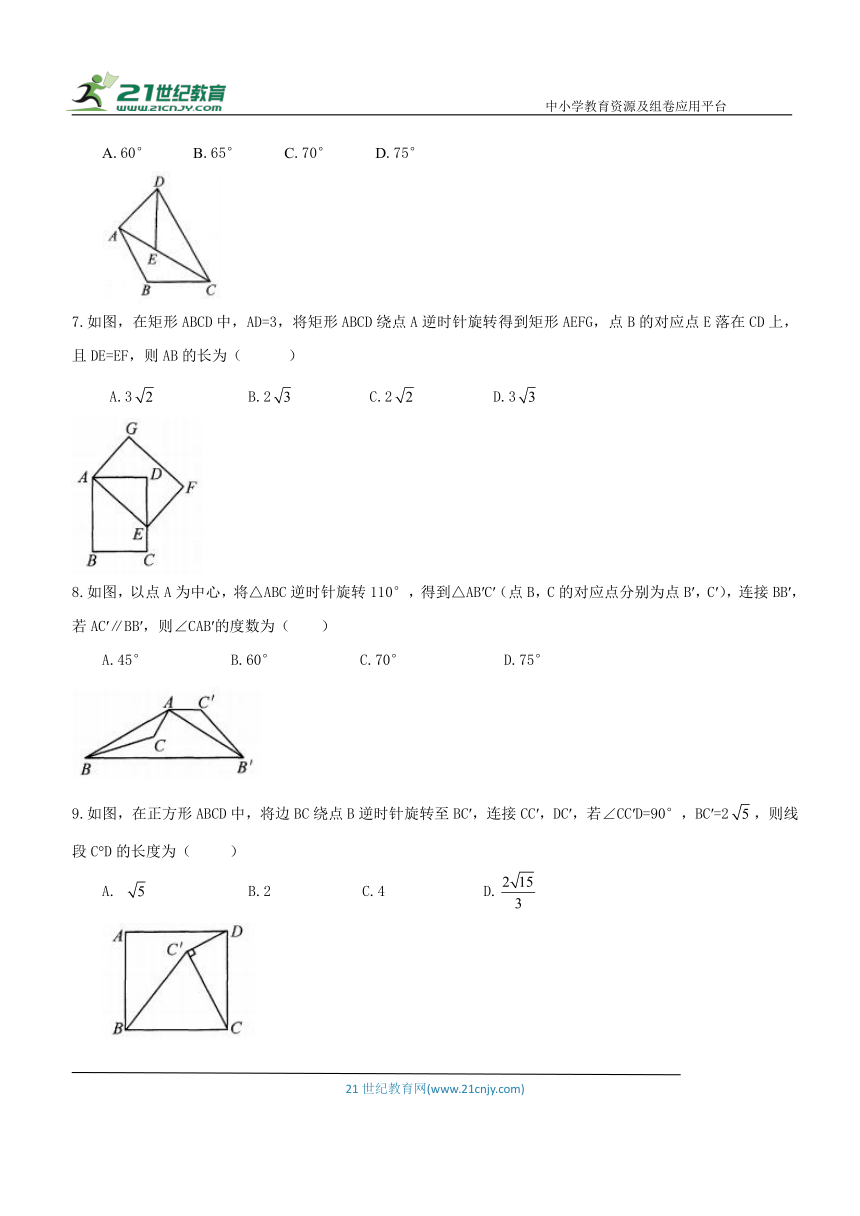
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
2.如图,将△OAB绕点O逆时针旋转75°到△OCD的位置,∠AOB=35°,则∠AOD等于( )
A.35° B.40° C.45° D.30°
3.下列几何图形中,不是中心对称图形的是( )
A.平行四边形 B.正六边形 C. 正五边形 D.正方形
4.如图,△ABC的顶点都在正方形网格格点上,如果将△ABC绕点O顺时针旋转90°,则点B的对应点B'的坐标是( )
A.(3,1) B.(1,3) C.(-3,-1) D.(-1,-3)
5.若点A(m,2)与点B(3,n)关于原点对称,则mn的值为( )
A.1 B. 5 C.1 D.5
6.如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A.60° B.65° C.70° D.75°
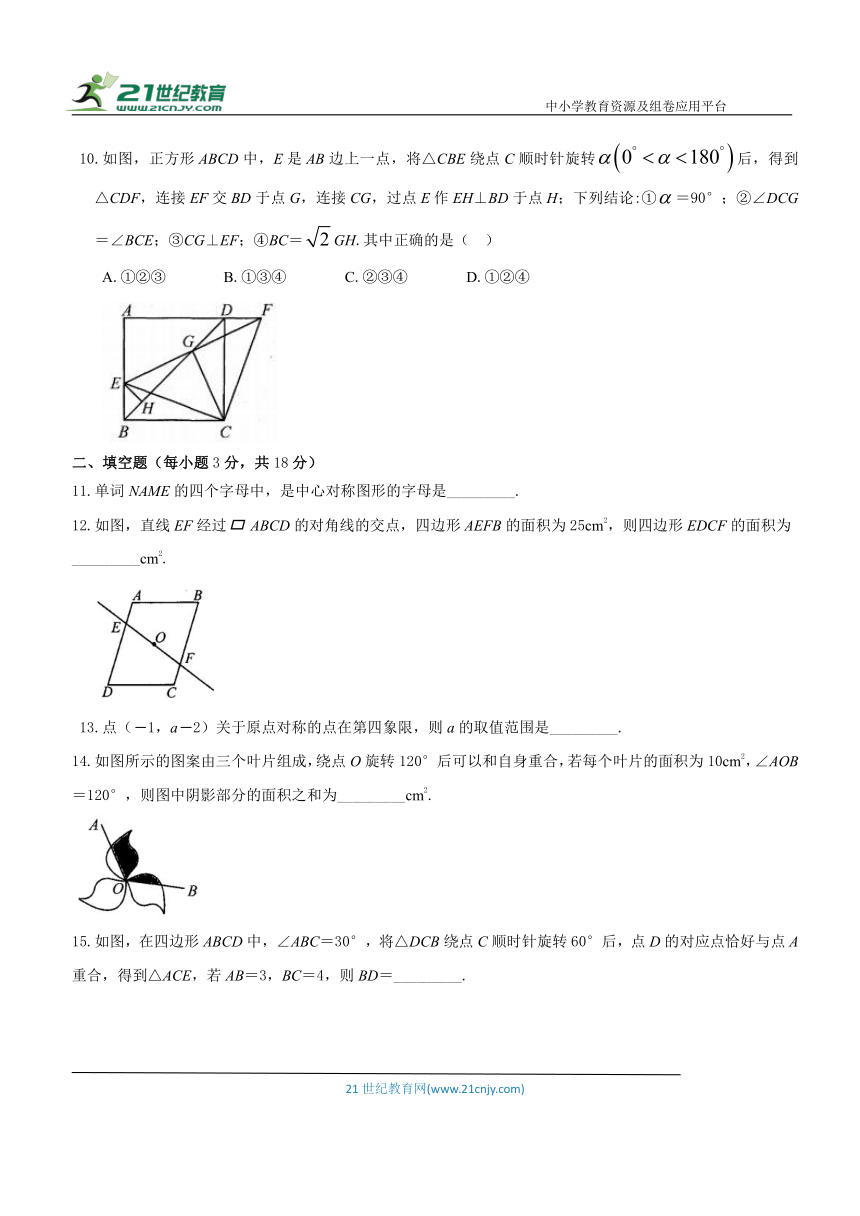
7.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( )
A.3 B.2 C.2 D.3
8.如图,以点A为中心,将△ABC逆时针旋转110°,得到△AB′C′(点B,C的对应点分别为点B′,C′),连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.45° B.60° C.70° D.75°
9.如图,在正方形ABCD中,将边BC绕点B逆时针旋转至BC′,连接CC′,DC′,若∠CC′D=90°,BC′=2,则线段C°D的长度为( )
A. B.2 C.4 D.
10.如图,正方形ABCD中,E是AB边上一点,将△CBE绕点C顺时针旋转后,得到△CDF,连接EF交BD于点G,连接CG,过点E作EH⊥BD于点H;下列结论:①=90°;②∠DCG=∠BCE;③CG⊥EF;④BC=GH.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每小题3分,共18分)
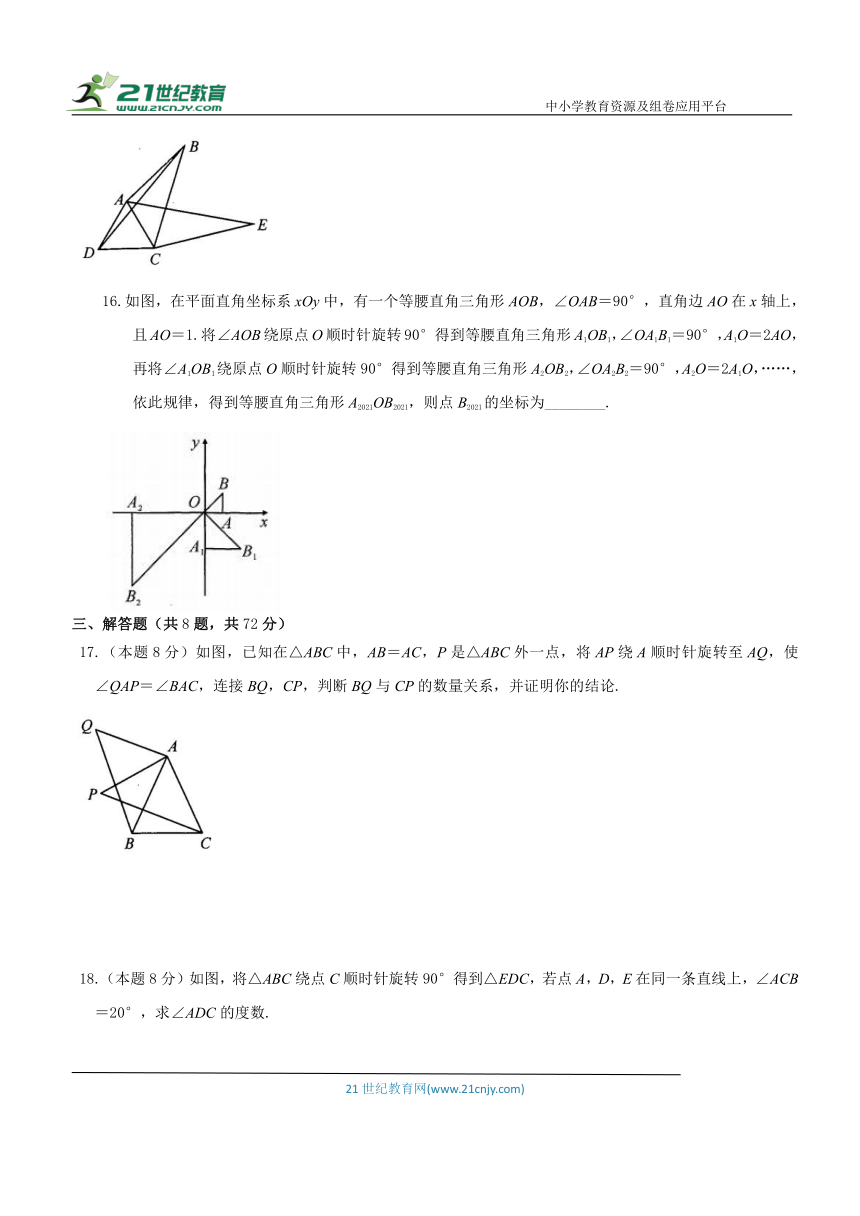
11.单词NAME的四个字母中,是中心对称图形的字母是_________.
12.如图,直线EF经过ABCD的对角线的交点,四边形AEFB的面积为25cm2,则四边形EDCF的面积为_________cm2.
13.点(1,a2)关于原点对称的点在第四象限,则a的取值范围是_________.
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为10cm2,∠AOB=120°,则图中阴影部分的面积之和为_________cm2.
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=_________.
16.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将∠AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,∠OA1B1=90°,A1O=2AO,再将∠A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,∠OA2B2=90°,A2O=2A1O,……,依此规律,得到等腰直角三角形A2021OB2021,则点B2021的坐标为________.
三、解答题(共8题,共72分)
17.(本题8分)如图,已知在△ABC中,AB=AC,P是△ABC外一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,判断BQ与CP的数量关系,并证明你的结论.
18.(本题8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,求∠ADC的度数.
19.(本题8分)如图,平面直角坐标系中,A(1,),将线段OA绕原点O顺时针旋转120°得到线段.(1)直接写出OA的长为_________;OA与x轴正半轴的夹角为_________°;
(2)求点的坐标.
20.(本题8分)如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点_________,旋转角度是_________度;
(2)若四边形AECF的面积为16,DE=1,求EF的长.
21.(本题8分)如图,在8×7的方格中,每个小正方形的顶点称为格点.图中A,B,C均为格点,E为AC与网格线的交点.用无刻度的直尺画图,画图过程用虚线,画图结果用实线.
(1)在图1中,先将△ABC绕点C顺时针旋转90°,得到△A1B1C(点A,B的对应点分别为点A1,B1),再画点E的对应点E1;
(2)在图2中,先在AC的左侧画格点F,使∠AFC=∠ABC,再在BC上画点M,使EM⊥FC.
22.(本题10分)△ABC和△ECD都是等边三角形.
(1)如图1,若B,C,D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系 说明理由.
23.(本题10分)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D在CA的延长线上,点E在边AB上,且AE=AD,M为BE的中点.
(1)直接写出的值为_______;
(2)将△ADE绕点A按顺时针旋转到图2的位置,连接AM,CD.试问(1)中的结论还是否成立?说明理由.
24.(本题12分)如图,四边形ABCD为正方形,E为正方形内一点,∠CEB=90°.将线段BE绕点B顺时针旋转90°,得到线段BF,连接AF,射线BE与AF交于点M.
(1)直接写出AE与CF的关系;
(2)求证:AM=MF;
(3)若BF=3,ME=1,求线段AF的长.
13九年级数学(上)第23章《旋转》单元检测卷
(考试范围:第23章综合测试解答考时间:120分钟满分:120分)
一、选择题(每小题3分,共30分)
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
答案:A
2.如图,将△OAB绕点O逆时针旋转75°到△OCD的位置,∠AOB=35°,则∠AOD等于( )
A.35° B.40° C.45° D.30°
答案:B
3.下列几何图形中,不是中心对称图形的是( )
A.平行四边形 B.正六边形 C. 正五边形 D.正方形
答案:C
4.如图,△ABC的顶点都在正方形网格格点上,如果将△ABC绕点O顺时针旋转90°,则点B的对应点B'的坐标是( )
A.(3,1) B.(1,3) C.(-3,-1) D.(-1,-3)
答案:A
5.若点A(m,2)与点B(3,n)关于原点对称,则mn的值为( )
A.1 B. 5 C.1 D.5
答案:D
6.如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A.60° B.65° C.70° D.75°
答案:D
7.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( )
A.3 B.2 C.2 D.3
答案:A
8.如图,以点A为中心,将△ABC逆时针旋转110°,得到△AB′C′(点B,C的对应点分别为点B′,C′),连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.45° B.60° C.70° D.75°
答案:D
9.如图,在正方形ABCD中,将边BC绕点B逆时针旋转至BC′,连接CC′,DC′,若∠CC′D=90°,BC′=2,则线段C°D的长度为( )
A. B.2 C.4 D.
答案:B
解析:过点作于点E,(AAS),
∵将边绕点逆时针旋转至,又 ,,故选B.
10.如图,正方形ABCD中,E是AB边上一点,将△CBE绕点C顺时针旋转后,得到△CDF,连接EF交BD于点G,连接CG,过点E作EH⊥BD于点H;下列结论:①=90°;②∠DCG=∠BCE;③CG⊥EF;④BC=GH.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
答案:B
解析:(1)旋转后与重合,,故(1)正确;(2),
当且仅当时,,故(2)不一定成立;
(3)作交于点,则,又 为等腰直角三角形,,故(3)正确;
(4)由(3)得,
即,故(4)正确.
二、填空题(每小题3分,共18分)
11.单词NAME的四个字母中,是中心对称图形的字母是_________.
答案:N
12.如图,直线EF经过ABCD的对角线的交点,四边形AEFB的面积为25cm2,则四边形EDCF的面积为_________cm2.
答案:25
13.点(1,a2)关于原点对称的点在第四象限,则a的取值范围是_________.
答案:
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为10cm2,∠AOB=120°,则图中阴影部分的面积之和为_________cm2.
答案:10
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=_________.
答案:5
16.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将∠AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,∠OA1B1=90°,A1O=2AO,再将∠A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,∠OA2B2=90°,A2O=2A1O,……,依此规律,得到等腰直角三角形A2021OB2021,则点B2021的坐标为________.
答解析:是等腰直角三角形,,
将绕原点顺时针旋转得到等腰直角三角形,且,再将绕原,点顺时针旋转得到等脰三角形,且,
依此规律,每4次循环一周,, 点与同在一个象限内,
∴点.
三、解答题(共8题,共72分)
17.(本题8分)如图,已知在△ABC中,AB=AC,P是△ABC外一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,判断BQ与CP的数量关系,并证明你的结论.
解:,证即可.
18.(本题8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,求∠ADC的度数.
答解将绕点顺时针旋转得到△EDC,
∵∠ADC是的外角,.
19.(本题8分)如图,平面直角坐标系中,A(1,),将线段OA绕原点O顺时针旋转120°得到线段.(1)直接写出OA的长为_________;OA与x轴正半轴的夹角为_________°;
(2)求点的坐标.
解:(1)2 60 (2)连交轴于点,由(1)得∴OD垂直平分..
20.(本题8分)如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点_________,旋转角度是_________度;
(2)若四边形AECF的面积为16,DE=1,求EF的长.
解:(1)A, 90; (2).
21.(本题8分)如图,在8×7的方格中,每个小正方形的顶点称为格点.图中A,B,C均为格点,E为AC与网格线的交点.用无刻度的直尺画图,画图过程用虚线,画图结果用实线.
(1)在图1中,先将△ABC绕点C顺时针旋转90°,得到△A1B1C(点A,B的对应点分别为点A1,B1),再画点E的对应点E1;
(2)在图2中,先在AC的左侧画格点F,使∠AFC=∠ABC,再在BC上画点M,使EM⊥FC.
21.
解:如图所示.
22.(本题10分)△ABC和△ECD都是等边三角形.
(1)如图1,若B,C,D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系 说明理由.
解:(1)证△ACD≌△BCE可得BE=AD;
(2)BC⊥DE
理由如下:延长BC交DE于M,∵∠ACB=60°,∠ACE=90°,
∴∠ECM=180°-∠ACB-∠ACE=30°,
∵△ECD是等边三角形,∴CM垂直DE,即BC⊥DE.
23.(本题10分)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D在CA的延长线上,点E在边AB上,且AE=AD,M为BE的中点.
(1)直接写出的值为_______;
(2)将△ADE绕点A按顺时针旋转到图2的位置,连接AM,CD.试问(1)中的结论还是否成立?说明理由.
23.
解:(1);(2)成立.理由如下:延长至点,使,连接是的中位线,,∴EN=2AM,∵AN=AB,AB=AC,∴AN=AC,∵∠BAC=90°,90°,
24.(本题12分)如图,四边形ABCD为正方形,E为正方形内一点,∠CEB=90°.将线段BE绕点B顺时针旋转90°,得到线段BF,连接AF,射线BE与AF交于点M.
(1)直接写出AE与CF的关系;
(2)求证:AM=MF;
(3)若BF=3,ME=1,求线段AF的长.
24.
24.解:(1);
(2)过点作的垂线,交的延长线于点正方形,
∴AB=BC,∠ABC=∠CEB=90°,∴∠CBE+∠ABE=90°,
∠CBE+∠BCE=90°,∴∠ABE=∠BCE,∴△ABN≌△BCE,
∴AN=BE=BF.∵AN⊥BM,∴∠N=90°=∠EBF.∵
∠NMA=∠BMF,∴△AMN≌△FMB,∴AM=MF;
(3)过点作的垂线,交的延长线于点.当点在的延长线上时,则,;当点在上时,则NM=BM=BE-ME=2,,
故或.
21世纪教育网(www.21cnjy.com)
13九年级数学(上)第23章《旋转》单元检测卷
(考试范围:第23章综合测试解答考时间:120分钟满分:120分)
一、选择题(每小题3分,共30分)
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
2.如图,将△OAB绕点O逆时针旋转75°到△OCD的位置,∠AOB=35°,则∠AOD等于( )
A.35° B.40° C.45° D.30°
3.下列几何图形中,不是中心对称图形的是( )
A.平行四边形 B.正六边形 C. 正五边形 D.正方形
4.如图,△ABC的顶点都在正方形网格格点上,如果将△ABC绕点O顺时针旋转90°,则点B的对应点B'的坐标是( )
A.(3,1) B.(1,3) C.(-3,-1) D.(-1,-3)
5.若点A(m,2)与点B(3,n)关于原点对称,则mn的值为( )
A.1 B. 5 C.1 D.5
6.如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A.60° B.65° C.70° D.75°
7.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( )
A.3 B.2 C.2 D.3
8.如图,以点A为中心,将△ABC逆时针旋转110°,得到△AB′C′(点B,C的对应点分别为点B′,C′),连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.45° B.60° C.70° D.75°
9.如图,在正方形ABCD中,将边BC绕点B逆时针旋转至BC′,连接CC′,DC′,若∠CC′D=90°,BC′=2,则线段C°D的长度为( )
A. B.2 C.4 D.
10.如图,正方形ABCD中,E是AB边上一点,将△CBE绕点C顺时针旋转后,得到△CDF,连接EF交BD于点G,连接CG,过点E作EH⊥BD于点H;下列结论:①=90°;②∠DCG=∠BCE;③CG⊥EF;④BC=GH.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每小题3分,共18分)
11.单词NAME的四个字母中,是中心对称图形的字母是_________.
12.如图,直线EF经过ABCD的对角线的交点,四边形AEFB的面积为25cm2,则四边形EDCF的面积为_________cm2.
13.点(1,a2)关于原点对称的点在第四象限,则a的取值范围是_________.
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为10cm2,∠AOB=120°,则图中阴影部分的面积之和为_________cm2.
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=_________.
16.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将∠AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,∠OA1B1=90°,A1O=2AO,再将∠A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,∠OA2B2=90°,A2O=2A1O,……,依此规律,得到等腰直角三角形A2021OB2021,则点B2021的坐标为________.
三、解答题(共8题,共72分)
17.(本题8分)如图,已知在△ABC中,AB=AC,P是△ABC外一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,判断BQ与CP的数量关系,并证明你的结论.
18.(本题8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,求∠ADC的度数.
19.(本题8分)如图,平面直角坐标系中,A(1,),将线段OA绕原点O顺时针旋转120°得到线段.(1)直接写出OA的长为_________;OA与x轴正半轴的夹角为_________°;
(2)求点的坐标.
20.(本题8分)如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点_________,旋转角度是_________度;
(2)若四边形AECF的面积为16,DE=1,求EF的长.
21.(本题8分)如图,在8×7的方格中,每个小正方形的顶点称为格点.图中A,B,C均为格点,E为AC与网格线的交点.用无刻度的直尺画图,画图过程用虚线,画图结果用实线.
(1)在图1中,先将△ABC绕点C顺时针旋转90°,得到△A1B1C(点A,B的对应点分别为点A1,B1),再画点E的对应点E1;
(2)在图2中,先在AC的左侧画格点F,使∠AFC=∠ABC,再在BC上画点M,使EM⊥FC.
22.(本题10分)△ABC和△ECD都是等边三角形.
(1)如图1,若B,C,D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系 说明理由.
23.(本题10分)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D在CA的延长线上,点E在边AB上,且AE=AD,M为BE的中点.
(1)直接写出的值为_______;
(2)将△ADE绕点A按顺时针旋转到图2的位置,连接AM,CD.试问(1)中的结论还是否成立?说明理由.
24.(本题12分)如图,四边形ABCD为正方形,E为正方形内一点,∠CEB=90°.将线段BE绕点B顺时针旋转90°,得到线段BF,连接AF,射线BE与AF交于点M.
(1)直接写出AE与CF的关系;
(2)求证:AM=MF;
(3)若BF=3,ME=1,求线段AF的长.
13九年级数学(上)第23章《旋转》单元检测卷
(考试范围:第23章综合测试解答考时间:120分钟满分:120分)
一、选择题(每小题3分,共30分)
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
答案:A
2.如图,将△OAB绕点O逆时针旋转75°到△OCD的位置,∠AOB=35°,则∠AOD等于( )
A.35° B.40° C.45° D.30°
答案:B
3.下列几何图形中,不是中心对称图形的是( )
A.平行四边形 B.正六边形 C. 正五边形 D.正方形
答案:C
4.如图,△ABC的顶点都在正方形网格格点上,如果将△ABC绕点O顺时针旋转90°,则点B的对应点B'的坐标是( )
A.(3,1) B.(1,3) C.(-3,-1) D.(-1,-3)
答案:A
5.若点A(m,2)与点B(3,n)关于原点对称,则mn的值为( )
A.1 B. 5 C.1 D.5
答案:D
6.如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A.60° B.65° C.70° D.75°
答案:D
7.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( )
A.3 B.2 C.2 D.3
答案:A
8.如图,以点A为中心,将△ABC逆时针旋转110°,得到△AB′C′(点B,C的对应点分别为点B′,C′),连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.45° B.60° C.70° D.75°
答案:D
9.如图,在正方形ABCD中,将边BC绕点B逆时针旋转至BC′,连接CC′,DC′,若∠CC′D=90°,BC′=2,则线段C°D的长度为( )
A. B.2 C.4 D.
答案:B
解析:过点作于点E,(AAS),
∵将边绕点逆时针旋转至,又 ,,故选B.
10.如图,正方形ABCD中,E是AB边上一点,将△CBE绕点C顺时针旋转后,得到△CDF,连接EF交BD于点G,连接CG,过点E作EH⊥BD于点H;下列结论:①=90°;②∠DCG=∠BCE;③CG⊥EF;④BC=GH.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
答案:B
解析:(1)旋转后与重合,,故(1)正确;(2),
当且仅当时,,故(2)不一定成立;
(3)作交于点,则,又 为等腰直角三角形,,故(3)正确;
(4)由(3)得,
即,故(4)正确.
二、填空题(每小题3分,共18分)
11.单词NAME的四个字母中,是中心对称图形的字母是_________.
答案:N
12.如图,直线EF经过ABCD的对角线的交点,四边形AEFB的面积为25cm2,则四边形EDCF的面积为_________cm2.
答案:25
13.点(1,a2)关于原点对称的点在第四象限,则a的取值范围是_________.
答案:
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为10cm2,∠AOB=120°,则图中阴影部分的面积之和为_________cm2.
答案:10
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=_________.
答案:5
16.如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将∠AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,∠OA1B1=90°,A1O=2AO,再将∠A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,∠OA2B2=90°,A2O=2A1O,……,依此规律,得到等腰直角三角形A2021OB2021,则点B2021的坐标为________.
答解析:是等腰直角三角形,,
将绕原点顺时针旋转得到等腰直角三角形,且,再将绕原,点顺时针旋转得到等脰三角形,且,
依此规律,每4次循环一周,, 点与同在一个象限内,
∴点.
三、解答题(共8题,共72分)
17.(本题8分)如图,已知在△ABC中,AB=AC,P是△ABC外一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,判断BQ与CP的数量关系,并证明你的结论.
解:,证即可.
18.(本题8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,求∠ADC的度数.
答解将绕点顺时针旋转得到△EDC,
∵∠ADC是的外角,.
19.(本题8分)如图,平面直角坐标系中,A(1,),将线段OA绕原点O顺时针旋转120°得到线段.(1)直接写出OA的长为_________;OA与x轴正半轴的夹角为_________°;
(2)求点的坐标.
解:(1)2 60 (2)连交轴于点,由(1)得∴OD垂直平分..
20.(本题8分)如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点_________,旋转角度是_________度;
(2)若四边形AECF的面积为16,DE=1,求EF的长.
解:(1)A, 90; (2).
21.(本题8分)如图,在8×7的方格中,每个小正方形的顶点称为格点.图中A,B,C均为格点,E为AC与网格线的交点.用无刻度的直尺画图,画图过程用虚线,画图结果用实线.
(1)在图1中,先将△ABC绕点C顺时针旋转90°,得到△A1B1C(点A,B的对应点分别为点A1,B1),再画点E的对应点E1;
(2)在图2中,先在AC的左侧画格点F,使∠AFC=∠ABC,再在BC上画点M,使EM⊥FC.
21.
解:如图所示.
22.(本题10分)△ABC和△ECD都是等边三角形.
(1)如图1,若B,C,D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系 说明理由.
解:(1)证△ACD≌△BCE可得BE=AD;
(2)BC⊥DE
理由如下:延长BC交DE于M,∵∠ACB=60°,∠ACE=90°,
∴∠ECM=180°-∠ACB-∠ACE=30°,
∵△ECD是等边三角形,∴CM垂直DE,即BC⊥DE.
23.(本题10分)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D在CA的延长线上,点E在边AB上,且AE=AD,M为BE的中点.
(1)直接写出的值为_______;
(2)将△ADE绕点A按顺时针旋转到图2的位置,连接AM,CD.试问(1)中的结论还是否成立?说明理由.
23.
解:(1);(2)成立.理由如下:延长至点,使,连接是的中位线,,∴EN=2AM,∵AN=AB,AB=AC,∴AN=AC,∵∠BAC=90°,90°,
24.(本题12分)如图,四边形ABCD为正方形,E为正方形内一点,∠CEB=90°.将线段BE绕点B顺时针旋转90°,得到线段BF,连接AF,射线BE与AF交于点M.
(1)直接写出AE与CF的关系;
(2)求证:AM=MF;
(3)若BF=3,ME=1,求线段AF的长.
24.
24.解:(1);
(2)过点作的垂线,交的延长线于点正方形,
∴AB=BC,∠ABC=∠CEB=90°,∴∠CBE+∠ABE=90°,
∠CBE+∠BCE=90°,∴∠ABE=∠BCE,∴△ABN≌△BCE,
∴AN=BE=BF.∵AN⊥BM,∴∠N=90°=∠EBF.∵
∠NMA=∠BMF,∴△AMN≌△FMB,∴AM=MF;
(3)过点作的垂线,交的延长线于点.当点在的延长线上时,则,;当点在上时,则NM=BM=BE-ME=2,,
故或.
21世纪教育网(www.21cnjy.com)
同课章节目录
